LCA(最近公共祖先)
LCA 就是最近公共祖先,表示为 \(\operatorname{lca}(a, b)\),它的求解方法主要有两种。
倍增法
这是最常用的一种可以动态求 LCA 的算法。时间复杂度为 \(O(\log{n})\)。
中心思想
这个算法中有两个特殊的数组:\(depth[i]\) 和 \(fa[i][k]\)。
\(depth[i]\):\(i\) 点的深度,以 \(root\) 为 \(0\)。
\(fa[i][k]\):从 \(i\) 点向上跳 \(2^k\) 步的点的序号。
对于两个点 \(a,b\),规定 \(depth[a] \ge depth[b]\)。
中心思想:我们先找到 \(a\) 上面深度和 \(b\) 相同的点,然后让这两个点同时向上跳,直到两个点刚开始重合,此点就是 \(a,b\) 的最近公共子节点。
对于中心思想里面的向上跳和查询深度就是靠 \(depth\) 和 \(fa\) 两个数组实现的。
思路很简单,正确行显而易见,最近重合的点肯定是最近公共祖先。
关于 \(depth\),用 bfs 或者 dfs 可以直接处理出来。
而 \(fa[i][k]\) 数组,我们有一个方法可以把它递推出来。我们向上跳 \(2^k\) 步,可以看作是,先跳 \(2^{k - 1}\) 步(到 \(fa[i][k - 1]\) 点),然后再跳 \(2^{k-1}\) 步,写成代码即 fa[i][j] = fa[fa[i][k - 1]][k - 1],而这一步也可以用 dfs 或 bfs 处理出来,起始条件为 fa[i][0] = f f 为 i 的父节点。
关于 \(fa[i][k]\) 中 \(k\) 的大小,原则上,只要大于点的数量的 \(\log_2\) 即可。而对于跳过 \(root\) 节点的情况,我们让它是 \(0\) 点,因为默认数组为 \(0\),可以不管它,这样在后面,只要是在 \(0\) 点就可以判断跳过了 \(root\),而且可以方边后面的操作。(跳过了 \(root\) 指向上跳的次数太多,把根节点 \(root\) 都跳过去了)
对于上面的把 \(a\) 跳到和 \(b\) 一个高度,我们 \(fa\) 数组是倍增跳跃的,且可以一次直接跳过根节点,因为任何数都可以变成一个二进制的形式,我们就可以把相差高度按二进制拆开来跳,保证最多 \(O(\log_2n)\) 的时间把 \(a\) 向上跳到和 \(b\) 想同的高度。在实现上,可以直接倒序枚举,\(k\) 让从大的开始,跳不过 \(b\) 的就跳,否则不跳,这样可以保证我们跳完了,\(a,b\) 同一深度。这里不懂可以看代码理解。
预处理时间复杂度 \(O(n\log{n})\),求解 LCA 时间复杂度为 \(O(\log{n})\)。
实操步骤
预处理
使用 dfs 或者 bfs 对 \(fa\) 和 \(depth\) 进行预处理。
- 进行 dfs,记录两个量,当前点 \(u\) 和 \(u\) 的父节点 \(f\)。
- 利用 \(f\) 的深度,更新 \(u\) 的深度,即
depth[u] = depth[f] + 1;,处理边界条件fa[u][0] = f,从 \(1\) 到点数的 \(\log_2\) (设为 \(k\)),即 从 \(1\) 到 \(k\) 枚举,利用转移方程fa[u][i] = fa[fa[u][i - 1]][i - 1](\(i\) 为枚举的数) 递推出 \(fa\) 数组。 - 枚举 u 的子节点,注意判断防止搜回去。
- 对每个 dfs 重复 \(2\) 到 \(3\)。
动态求解 LCA
- 对 a,b 进行求解。
- 判断 \(depth\) 大小,使得 \(depth[a] \ge depth[b]\)。
- 进行向上跳的操作,倒序枚举 \(k\),如果跳后深度不超过 \(depth[b]\) 就进行跳跃,否则不跳
- 跳完,\(a,b\) 一定在同一高度,这时候要判断一下 \(a,b\) 是否同一点,如果是,直接输出 \(a\) 或 \(b\)
- 进行同时向上跳的操作,倒序枚举 \(k\) ,如果跳后 \(a,b\) 不是同点则继续向上跳,否则不跳。(这里解释一下,这里的原理和第 3 步差不多,但不尽相同。我们设置 \(fa\) 跳过 \(root\) 都是 \(0\),如果跳过了 \(root\),因为相同不跳,所以可以排除这些情况。而对于非跳过 \(root\) 的情况,\(a,b\) 相同说明是 \(a,b\) 的祖宗节点,但是,这不一定是最近的,所以会错误。相反,如果相同的不跳,根据第 \(3\) 步的原理,我最后会跳到一个距离最近祖先最近的非祖先节点,即祖先节点下面一个点,这时候无论是 \(a\) 还是 \(b\) 只要再向上跳一个,就一定是最近公共祖先)。
- 向上跳完后,\(a,b\) 任意一个向上跳一步,就是最近公共祖先,即 \(fa[a][0]\) 或者 \(fa[b][0]\)。
- 输出 \(fa[a][0]\) 或者 \(fa[b][0]\)。
代码
显而易见的代码。
预处理推荐 dfs,比较易写不易错
预处理 dfs
void dfs(int u, int f)
{
depth[u] = depth[f] + 1;
fa[u][0] = f;
for (int i = 1; i <= 15; i ++ )
fa[u][i] = fa[fa[u][i - 1]][i - 1];
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == f) continue;
dfs(j, u);
}
}
预处理 bfs
void bfs(int root)
{
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[root] = 1;
int tt = 0, hh = 0;
q[hh] = root;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (depth[j] > depth[t] + 1)
{
depth[j] = depth[t] + 1;
fa[j][0] = t;
q[ ++ tt] = j;
for (int k = 1; k <= 15; k ++ ) fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
动态求解LCA
int lca(int a, int b)
{
if (depth[a] < depth[b]) swap(a, b);
for (int k = 15; k >= 0; k -- )
if (depth[fa[a][k]] >= depth[b])
a = fa[a][k];
if (a == b) return a;
for (int k = 15; k >= 0; k -- )
if (fa[a][k] != fa[b][k])
{
a = fa[a][k];
b = fa[b][k];
}
return fa[a][0];
}
向上标记法
算是比较劣质的算法,不太可以离线,每次查询最坏时间复杂度为 \(O(n)\)。
基本上不用,只给思想。
中心思想
设求 \(a,b\) 的最近公共祖先,
从 \(a\) 点先不断向上标记,包括它本身,然后从 \(b\) 点向上走,遇到的第一个被标记的点就是它们的最近公共祖先。如下图。
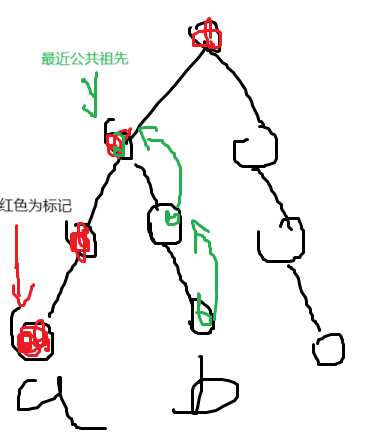
正确性显而易见。
虽然说是 \(O(n)\) ,但是实现起来,空间时间都比较差,大部分情况下动态使用是 \(O(n)\) 的,和Tarjan 的 \(O(n + m)\) 离线不一样。并不优秀。
Tarjan
每错,又双叒叕是 Tarjan。
这是一种离线的做法,时间复杂度为 \(O(n + m)\) ,\(n\) 是节点数,\(m\) 是询问数
其本质相当于对向上标记法的优化。
中心思想
这里把树上的点分为了三类
- 已经被搜完的点(即点所在的函数已经结束了)
- 正在被搜的点(即点所在的函数没有结束)
- 未搜的点(还没开始搜到)
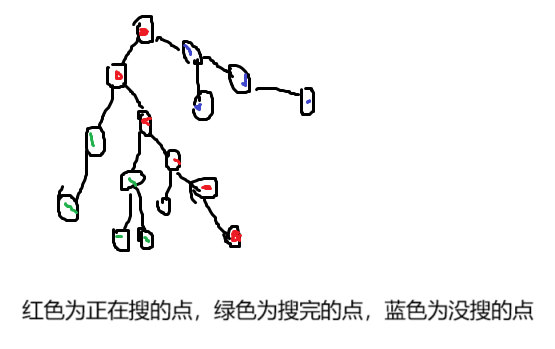
以下根据图片讲解。
我们能发现一件事,正在被搜的点(下面简称红点)一定成一条链,因为是正在被搜,不是在当前函数中,就是在之前转移来的函数中,因此一条链。所有已经被搜完的点(绿点)和红点都有接触(因为不可能和蓝点有接触),如果把某个绿点 j 归为对应最近的红点 k 之内的话,那个红点 k,就是现在红点 u 和 j 的最大公共祖先。可以把这里的红点看作上面向上标记法中的标记,那么原理就显而易见了。而这样,在 u 时可以求出来,所有绿点和 u 的最大公共祖先。
对于把 j 和 k 合并成一个点,我们只需要用到并查集,而这个搜索是在 dfs 中的,每个点只搜一遍。而我们是离线算法,并查集查询后可以把所有的答案存下来。因此可知查询是 \(O(1)\) 的,而每个点遍历一遍是 \(O(n)\),有 \(m\) 次查询,总的时间复杂度就是 \(O(n + m)\) 的。当然这个时间复杂度也不是太严谨,因为并查集不总是 \(O(1)\) 的时间复杂度。
对于每个点的状态我们分为 \(1,2,0\) 三种,对应,正在搜的点,未搜的点,已经被搜完的点。
实操步骤
- 进行 tarjan,设当前点为 \(u\)
- 把 \(u\) 的状态设置为 \(1\)
- 枚举子节点,把没进行的点进行 tarjan,完成后把子节点和父节点合并成一个集合。
- 枚举和 \(u\) 点有关的问题,如果对应点在已经完成点即状态为 \(2\) 的话,查询并查集,记录结果
- 循环 \(1\) 到 \(4\) 步
代码
很简单 awa
void tarjan(int u)
{
st[u] = 1;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (st[j]) continue;
tarjan(j);
p[j] = u;
}
for (auto itme : query[u])
{
int y = itme.y, id = itme.id;
if (st[y] == 2) res[id] = find(y);
}
st[u] = 2;
}




