洛谷P1268 树的重量

题目链接

第一次用博客园啊, 写的不好请见谅;

下面说说题目
题目让求这几个点为叶节点形成的树的边权和, 但是我们可以抽象一下, 看成是在给定两个点的线段上不断加线段, 使其成为一棵树.
这样说可能不好懂, 见下图

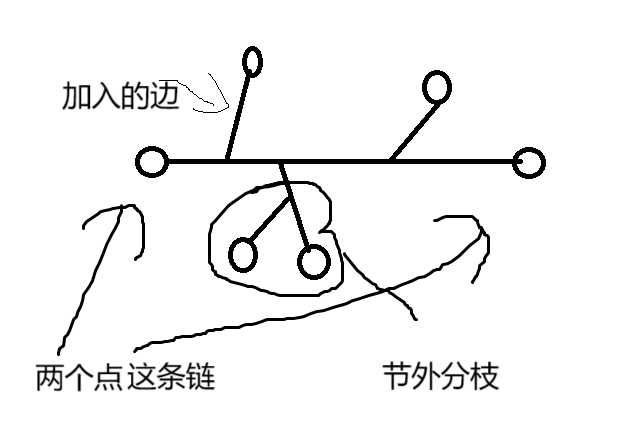
图中的圆圈是叶节点

题目就是求以这几个点为叶节点的树(设为E)的最小边权和
为什么是最小, 因为树中每两个叶节点之间的距离都是最小的, 如果要满足任意两点都是最小
那么整个树的边权和就是最小的, 这里不能严谨的证明, 假设有比它边权和还小的情况(设为G)
那么树G中一定有一条对应边小于树E, 那么通过这条边就能缩小我们原树, 那么树E就能<= G
还是最小的, 这里不太严谨, 欢迎指出错误

这里我们可以把他进行转化, 变为在两个点形成的线段上, 直接加线段(相当于加点),
通过不断加线段使它形成一棵树, 而我们只需要求这样形成的树的最小值就行了

怎么加边, 在ab这条链上, 我们设s为当前要加进去的点(线段), 那么这条新线段的长度就是res = (g[s][a] + g[s][b] - g[a][b]) / 2
但是不止这样的情况, 因为这条边可以连在其他已经加进去的线段上, 这里叫"节外分枝"
如果想要"节外分枝"的话首先需要满足这条边(这个点i)到两端点的距离都大于等于, 原边(k)连到
链上的点(j, 非叶节点)到两端点的距离, 形式化的说g[j][a] >= g[i][a], g[j][b] >= g[i][a]
满足条件后新加入的边的长度就是, res.s - (res.s + res.k - g[s][k]) / 2 这就是新加入的边长
因为链上有很多边, 所以去我们取里面的最小值即可

并且为了防止出现在加边在链外的情况, 这里的链最好选取 最长"最短路径"的两点

时间上129ms, 是O(n ^ 2)的做法, 因为数据范围太小了, 所以就水过去了

具体见代码吧

/*
    就是求以这几个点为叶节点的树(设为E)的最小边权和
    为什么是最小, 因为树中每两个叶节点之间的距离都是最小的, 如果要满足任意两点都是最小
    那么整个树的边权和就是最小的, 这里不能严谨的证明, 假设有比它边权和还小的情况(设为G)
    那么树G中一定有一条对应边小于树E, 那么通过这条边就能缩小我们原树, 那么树E就能<= G
    还是最小的, 这里不太严谨, 欢迎指出错误
    
    这里我们可以把他进行转化, 变为在两个点形成的线段上, 直接加线段(相当于加点), 
    通过不断加线段使它形成一棵树, 而我们只需要求这样形成的树的最小值就行了
    
    怎么加边, 在ab这条链上, 我们设s为当前要加进去的点(线段), 那么这条新边的长度就是res = (g[s][a] + g[s][b] - g[a][b]) / 2
    但是不止这样的情况, 因为这条边可以连在其他已经加进去的线段上, 这里叫"节外分枝"
    如果想要"节外分枝"的话首先需要满足这条边(这个点i)到两端点的距离都大于等于, 原边(k)连到
    链上的点(j, 非叶节点)到两端点的距离, 形式化的说g[j][a] >= g[i][a], g[j][b] >= g[i][a]
    满足条件后新加入的边的长度就是, res.s - (res.s + res.k - g[s][k]) / 2 这就是新加入的边长
    因为链上有很多边, 所以去我们取里面的最小值即可
    
    并且为了防止出现在链外的情况, 这里的链最好选取最长 最短距离 的两点
    
    具体见代码吧
    
*/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>

using namespace std;

const int N = 40;

int g[N][N];
int n, m;

struct Node
{
    int a, b, w, id;
}maxv;
vector<Node> e; // 记录加入的原边

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )  
        for (int j = i + 1; j <= n; j ++ )
        {
            auto &v = maxv;
            cin >> g[i][j], g[j][i] = g[i][j]; // 存图, 最短两点距离
            if (g[i][j] > v.w) // 求最长两点
                v = {i, j, g[i][j]};
        }
        
    int ans = maxv.w; // 原链的长度不要忘记加上
    for (int i = 1; i <= n; i ++ )
    {
        auto &v = maxv;
        int a = g[i][v.a], b = g[i][v.b], minv;
        int res = (a + b - v.w) / 2; // 新边长度
        if (v.a == i || v.b == i) continue; // 跳过两端点(因为已经在链上, 在两端上), 不加一样过
        minv = res; 
        for (auto j : e) // 在原有边上"节外生枝"
            if (j.a <= a && j.b <= b) 
                minv = min(minv, res - (res + j.w - g[j.id][i]) / 2);
        // 每条边都要加入, 不然就要更新一下这条边的最长值, 
        e.push_back({a - res, b - res, res, i}); // 如果没"节外生枝"了, 需要把这条边也加入到可以节外生枝的边(原边)里面, a - res和b - res是加入这条边的条件(最起码能碰到这条边)
        ans += minv; 
    }
    cout << ans << endl;
    return 0;
}