结队编程作业
Github地址
分工情况:
| 姓名 | 分工 |
|---|---|
| 方梓涵:博客 | 原型设计,编写代码 |
| 鲍凌函 | 测试代码,编写博客 |
2.1 - 原型设计
[2.1.1]设计说明
设计思路:
做一个网页游戏,将网页页面分为三个区域,拼图区,提示区,按钮区
一共设置五个按钮:开始按钮,重新开始按钮,更换图片按钮,提示步数按钮,动画演示按钮将会自动完成拼图操作,途中玩家不可点击图片和按钮。
在按钮组上方设置一个大 DIV即拼图区域,平均分成九个正方形,用来包裹里面的小块,并且从 1 开始编号。
在页面左上角设置提示区用来显示原图,规则说明和步数时间。
页面设计展示:
原始页面:
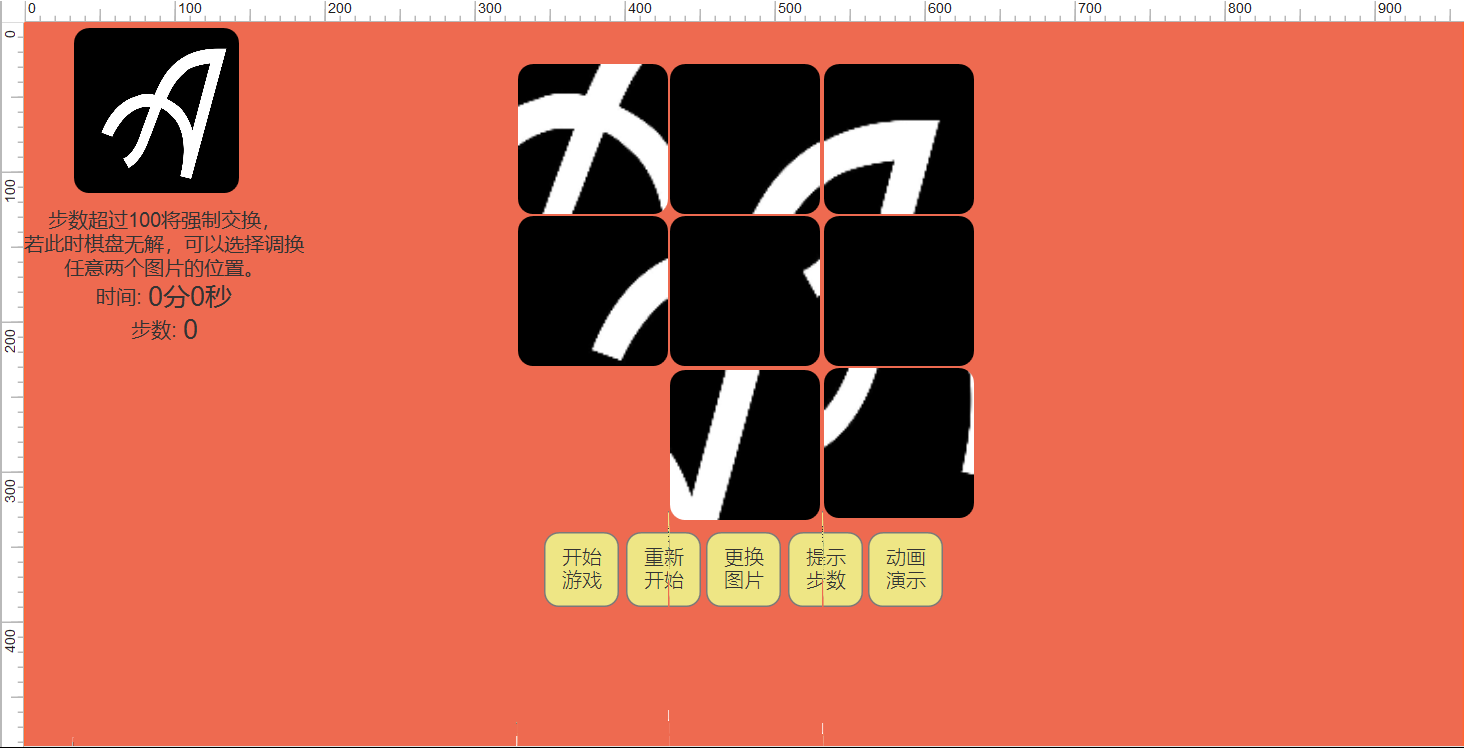
开始页面: 点击开始的时候开始计时,再次点击可以暂停游戏停止计时;

步数提示: 点击步数提示会在拼图区域上方显示最小步数和空白格移动路线;

强制交换: 当步数超过设定的值,将弹出步数超出弹出框进行强制交换,若无解将在拼图区域上方出现输入栏供玩家输入要交换的两张图片序号,点击确定完成交换。
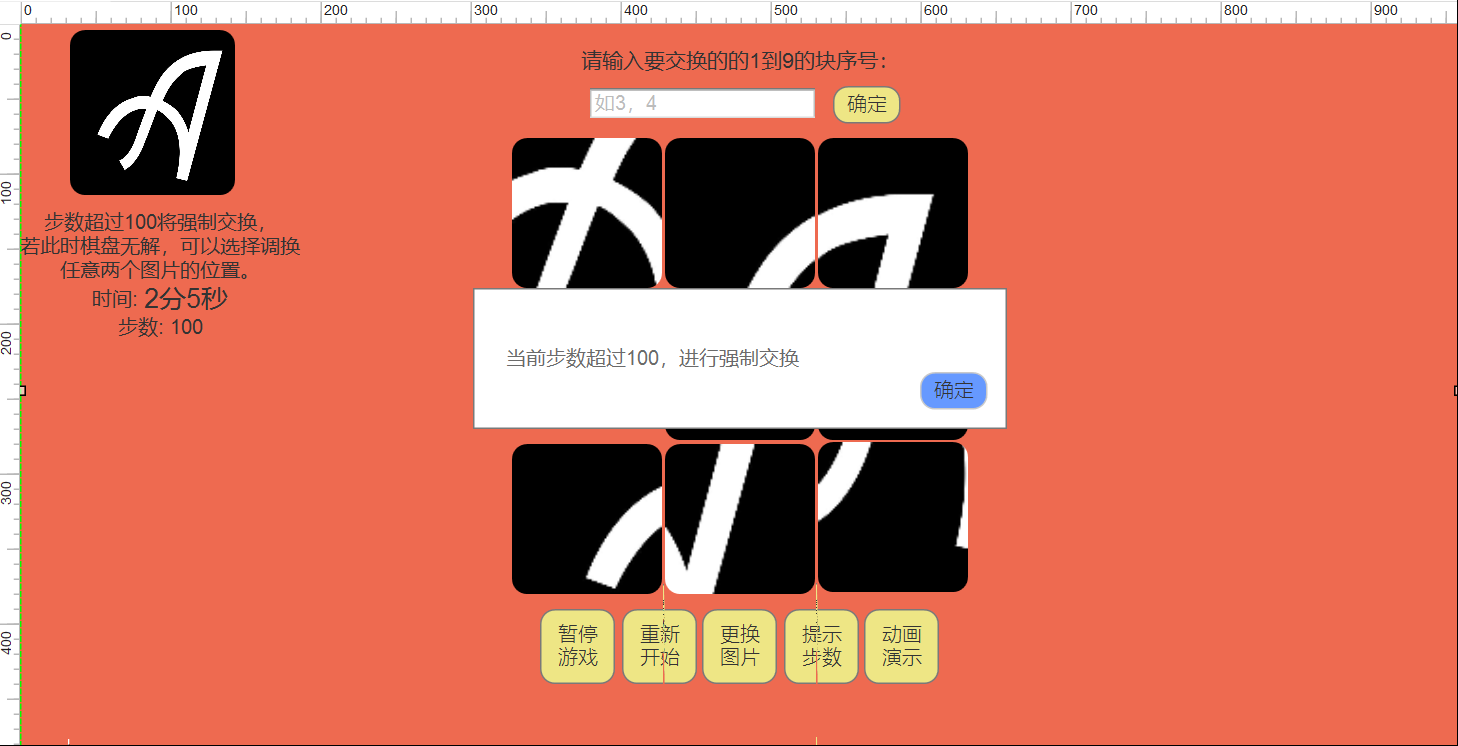
成功页面: 完成拼图后停止计时,并弹出成功页面,成功页面显示步数和完成时间,点击重新开始按钮,打乱图片重新开始游戏。
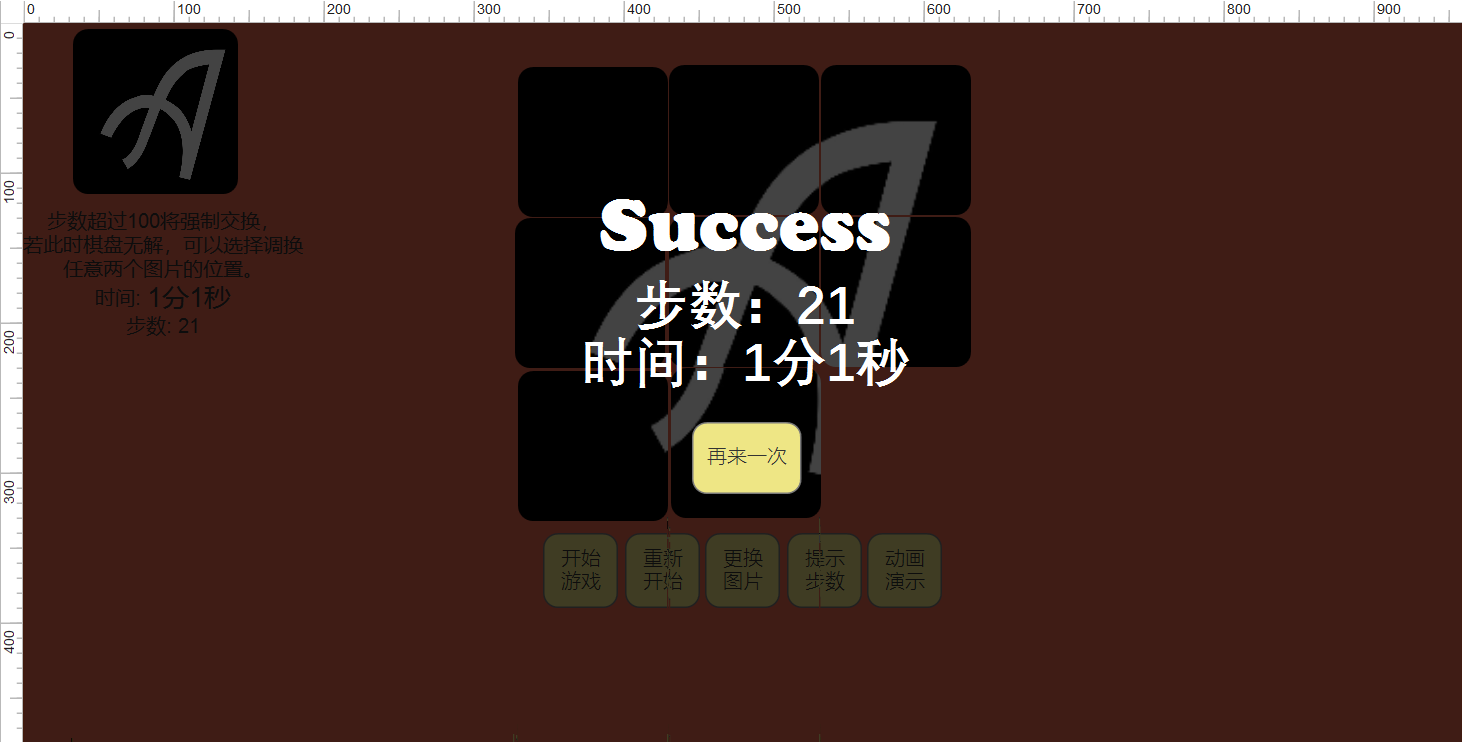
[2.1.2]原型模型设计工具实现:Axure Rp
[2.1.3]结对的过程:
没有犹豫,直接选了坐在旁边的舍友。

[2.1.4]遇到的困难及解决方法:
刚开始原型设计时,因为前端语言编程能力不够强,无法呈现出想要的页面,最后妥协,用了最简洁最方便的页面。
2.2 - AI与原型设计实现
[2.2.1]代码实现思路:
①设计思路:
八数码问题所要解决的东西是什么,即将一幅图分成3*3的格子其中八个是图一个空白,俗称拼图游戏,我们可以抽象为现有数字1-9在九宫格中,随机选取其中一个小块将其隐藏设置为空白格并且将其编号设为0,打乱九个小块顺序。并且保存一个开始状态数组和结束状态数组(即将图片原始状态的编号顺序),现在需要求解出从初始状态到结束状态所需要的最小步数与过程。
②主要函数:
| 函數名 | 功能 |
|---|---|
| startAndStop() | 开始游戏 |
| reset() | 重置,将时间步数清空,打乱图片 |
| change() | 更换拼图图片 |
| pointer() | 向用户提示最小步数和路线 |
| cheater() | 用动画形式向用户演示 |
| judgeHaveSolution() | 用逆序数的方式判断当前布局是否有解 |
| randomLayout() | 随机打乱图片 |
| move(from_number) | 移动图片 |
| judge() | 判断是否进行强制交换或是否当前布局成功 |
| doubleBFS() | 利用双向广度搜索求解最小步数和最优路线 |
| enforce() | 随机选取两个非空白格的小块进行强制调换 |
| exchange() | 用户自定义两个小块进行交换 |
③部分流程图:
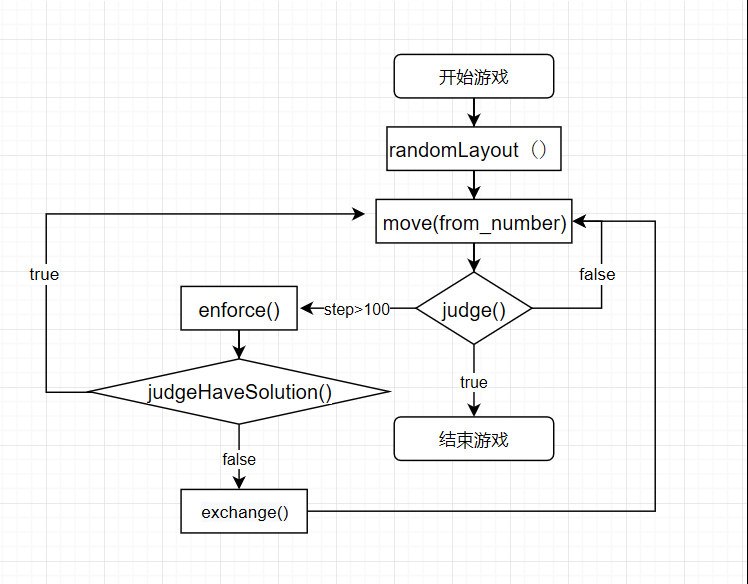
④算法原理:
双向bfs适用于知道起点和终点的状态下使用,从起点和终点两个方向开始进行搜索,可以非常大的提高单个bfs的搜索效率
双向广度优先算法从两个方向以广度优先的顺序同时扩展,一个是从起始节点开始扩展,另一个是从目的节点扩展,直到一个扩展队列中出现另外一个队列中已经扩展的节点,也就相当于两个扩展方向出现了交点,那么可以认为我们找到了一条路径。
用一张图来进行说明
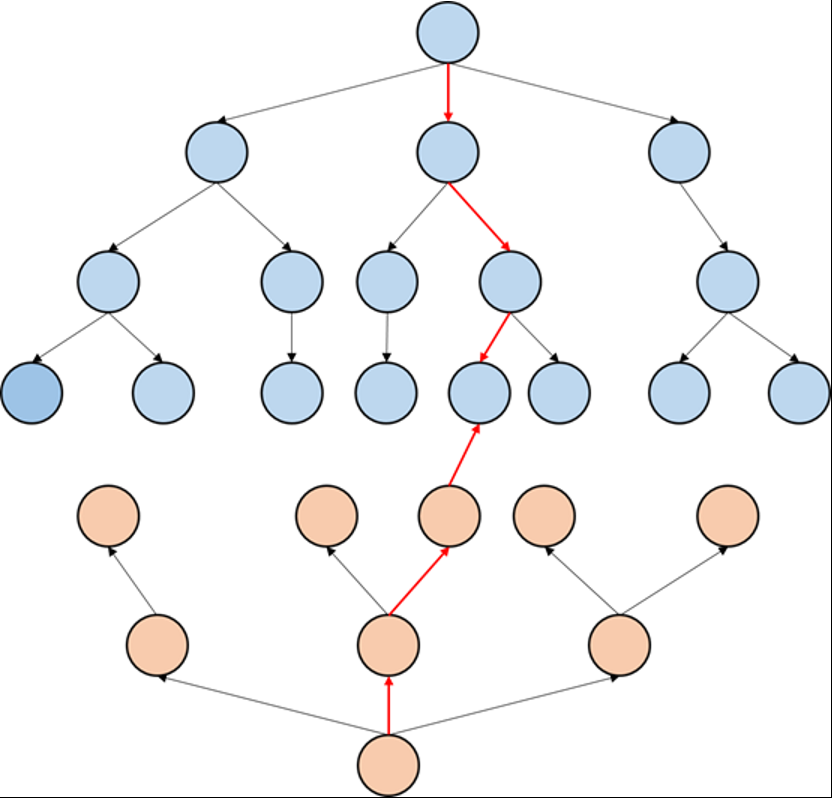
当两种颜色相遇的时候,说明两个方向的搜索树遇到一起,这个时候就搜到了答案。
⑤算法实现流程说明:
- 首先我们需要将八数码中即1-9这九个数的每一种组合当做一种状态,那么按照排列组合定理我们可以求出八数码可能存在的状态数:9!即362880种排列组合。
在遍历状态的过程中,可以将二维数组转化为数字或字符串,如123456780。在变为字符串后便可以直接判断该状态是否等于最终状态,因为从数组变为了字符串或数字的基本类型就可以直接比较是否相等。
**2. 当鼠标点击其中一个方块时,如何判断当前方块是否可移动? **
因为对于0的移动限定是有一定空间边界的,比如0如果在第二行的最右边,那么0只能进行左上下三种移动方式。
因此设置一个一维数组变量,用来保存小 DIV 的编号,从1到9开始编号。如果小DIV的编号为 0,则它为空白块。 然后再设置一个二维数组变量,用来保存不同位置的小块可去的位置。
var s_can_walk = new Array([0,0],[2,4],[1,3,5],[2,6],[1,5,7],[2,4,6,8],
[3,5,9],[4,8],[5,7,9],[6,8]);
比如小块编号为 1 的,它只能向 2号,4号这两个方向移动。又比如 5,它能向 2、4、6、8 这四个方向移动。每次点击小块都要循环这个数组,判断对应的方向是否有编号为0的小块,如果有,那么它就可以往这个方向移动了。
3.将每种状态转化为二维数组后,就可以配合双向广搜来进行遍历。初始状态可以分别设定为广搜中图的第一层和最后一层,由初始状态通过判断0的移动方向可以得到不大于4种状态的子节点,同时需要维护两个对象来分别记录两个方向的路径,出现过则无需再压入队。至此反复求出节点的子节点并无重复的压入队。
var route; //路线里0是右,1是左,2是下,3是上
//step记录每一个状态的步数(有可能由q1扩展的步数,也有可能是由q2扩展的步数)
var step = new HashTable();
//state中value=1表示从前部BFS(q1)扩展的,value=2表示从后部BFS(q2)扩展的的,如果出现两个状态相加为3说明找到路径
var state = new HashTable(); //map<string, int>
var route1 = new HashTable(); //map<string, string>
var route2 = new HashTable();
var q1 = new Queue();
var q2 = new Queue();
var dir = new Array([0,1],[0,-1],[1,0],[-1,0])
var str1 = "";//str1是移动前九宫格的字符串形式
var str2 = "";//str2是移动后九宫格的字符串形式
var str = "";
var flag = 0;
var BFSx = 0;
var BFSy = 0;
//first为当前布局
//last为最后应得的正确结果[12345678.]
function doubleBFS(){
q1.push(first);
q2.push(last);
step.add(first,0);
step.add(last,0);
//起始点作为前部BFS的起点(=1),终点作为后部BFS的起点(=2)
state.add(first,1);
state.add(last,2);
route1.add(first,"");
route2.add(last,"");
while(!q1.empty() && !q2.empty()){
if(q1.dataStore.length < q2.dataStore.length){//每次选择待扩展节点少的那个方向进行扩展
str1 = q1.front();
q1.pop();
flag = 1;//表示后续变换状态入q1队列
}
else{
str1 = q2.front();
q2.pop();
flag = 2; //表示后续变换状态入q2队列
}
//把字符串变成九宫字符数组
for (var i = 0; i < str1.length; i++) {
m[(i-(i % 3)) / 3][i % 3] = str1[i];
}
for (var i = 0; i < 3; i++) { //找空格在的位置
for (var j = 0; j < 3; j++) {
if(m[i][j]== '.'){
BFSx = i;
BFSy = j;
break;
}
}
if(m[i][j]==".") break;
}
//当前状态进行上下左右方向移动
for (var i = 0; i < 4; i++) {
str2 = ""; //每次寻找时都清零,不然会累计
var tx = BFSx + dir[i][0];
var ty = BFSy + dir[i][1];
//判断是否越界
if((tx>=0 && tx<3) && (ty>=0 && ty<3)){ //交换0值和移动方向的数字
var temp = m[BFSx][BFSy];
m[BFSx][BFSy] = m[tx][ty];
m[tx][ty] = temp; //tx,ty是0值坐标
for (var j = 0; j < 3; j++) {
for (var k = 0; k < 3; k++) {
str2 += m[j][k];
}
}
if(!step.containsKey(str2)){//当前状态未被扩展过
step.add(str2,step.getValue(str1) + 1) ;//步数=原数字步数+1
state.add(str2,state.getValue(str1) ) ;//更新状态,与原数字的来源(前部还是后部BFS)相同
str = i.toString();//0是右,1是左,2是下,3是上
if(flag == 1 ){
q1.push(str2);
route1.add(str2,route1.getValue(str1) + str) ;
}else if(flag==2){
q2.push(str2);
route2.add(str2,route2.getValue(str1) + str) ;
}
}
//搜索范围重叠,出现答案
else{
str = i.toString();//0是右,1是左,2是下,3是上
if(flag == 1 ){
route1.add(str2,route1.getValue(str1) + str) ;
}else if(flag==2){
route2.add(str2,route2.getValue(str1) + str) ;
}
//相加为3说明找到路径(还有可能是=2或者=4,都是由相同方向的BFS已经扩展过的点,不需要处理)
if(state.getValue(str1) + state.getValue(str2) == 3){
var ans = step.getValue(str1) + step.getValue(str2) +1;
var ahead_route;
var later_route;
var change_later_route = "";
var r12 = route1.getValue(str2);
var r22 = route2.getValue(str2);
ahead_route=r12;
later_route=r22;
later_route = later_route.split('').reverse().join('');
//从目的节点找到的路径与从开始结点找到的路径相反,所以要反过来
for (var i = 0; i < later_route.length; i++) {
if(later_route[i]=="0") change_later_route += "1";
else if(later_route[i]=="1") change_later_route += "0";
else if(later_route[i]=="2") change_later_route += "3";
else if(later_route[i]=="3") change_later_route += "2";
}
route = ahead_route + change_later_route ;//记录每一步移动的方向
return ans;
}
}
//因为最多有上下左右移动四种情况,每一次移动后再找另一种情况需要复原
var temp = m[BFSx][BFSy];
m[BFSx][BFSy] = m[tx][ty];
m[tx][ty] = temp;
}
}
}
return -1;
}
4.如何判断目前布局是否有解?
如果真的像拼图一样,从一个已知状态打散到另一个状态,那么肯定是可以复原的。但是我们现在的打乱策略是任意的,所以我们需要判断起始状态是否可以达到结束状态。判断方式是通过起始状态和结束状态的逆序数是否同奇偶来判断。
逆序数:在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。一个排列中所有逆序总数叫做这个排列的逆序数。
如果起始状态与结束状态的逆序数的奇偶性相同,则说明状态可达,反之亦然。至于为什么,下面通过简单的例子来试图说明并推广到整个结论:
- 起始状态为[[1,2,3],[4,5,6],[7,8,0]]
- 可以看做字符串123456780
- 结束状态为[[1,2,3],[4,5,6],[7,0,8]]
- 可以看做字符串123456708
这个变换只需要一步,即0向左与8进行交换。那么对于逆序数而言,0所在的位置是无关紧要的,因为它比谁都小,不会导致位置变化逆序数改变,即0的横向移动不会改变逆序数的奇偶性,所以我们可以忽略空白格的位置。 - 起始状态为[[1,2,3],[4,5,6],[7,8,0]]
- 可以看做字符串123456780
- 结束状态为[[1,2,3],[4,5,0],[7,8,6]]
- 可以看做字符串123450786
这个变换同样只需要一步,即0向上与6进行交换。我们已知0的位置不会影响逆序数的值。那么现在我们只需要关注6的变化。6从第6位置变为第9位置,导致7与8所在位置之前的逆序数量出现了变化。7、8都比6大,则整体逆序数量会减少2,但是逆序数-2仍然保持了奇偶性。与此同时我们可以知道,当0纵向移动的时候,中间的两个数(当前例子7、8的位置)只会有三种情况。要不都比被交换数大(比如7、8比6大)要不一个大一个小,要不都小。如果一大一小,则逆序数仍会保持不变,因为总量上会是+1-1;都小的话则逆序数会+2,奇偶性同样不受到影响。故我们可以认为,0的横向与纵向移动并不会改变逆序数的奇偶性。从而我们可以在一开始通过两个状态的逆序数的奇偶性来判断是否可达。
代码实现:
function judgeHaveSolution(){
var inversion_number=0; //逆序数
for (var i = 1; i < s.length; i++) {
//i在前,j在后,求逆序数,从1求到9,要去掉空白块再排列
if(s[i]==0) continue;
for (var j = i+1; j < s.length; j++) {
if(s[j]==0) continue;
if(s[i]>s[j]) inversion_number++;
}
}
// 逆序数为偶数,则返回有解,反之返回无解,
if(inversion_number%2==0){
return true;
}else {
return false
};
}
⑥性能分析与改进
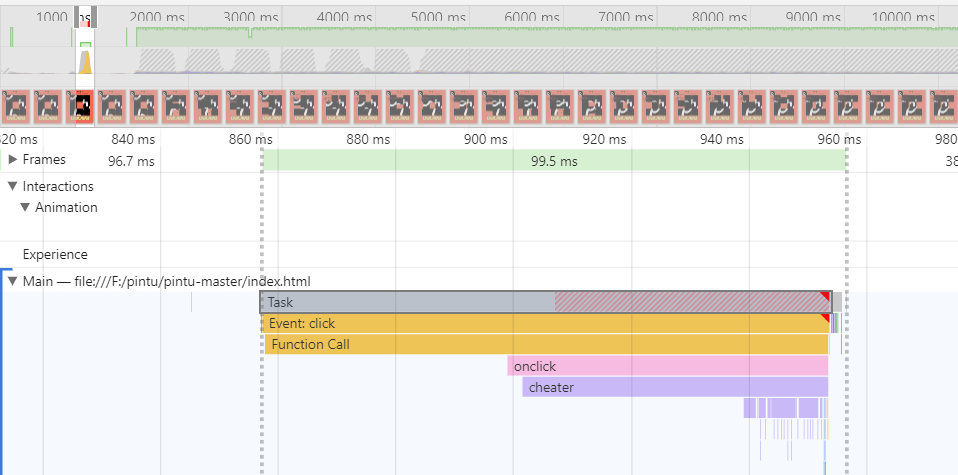
点进红三角形的模块,消耗最大的是function call(函数调用,只有当浏览器进入到js引擎中时触发),接着是算法的函数(cheater,doubleBFS)
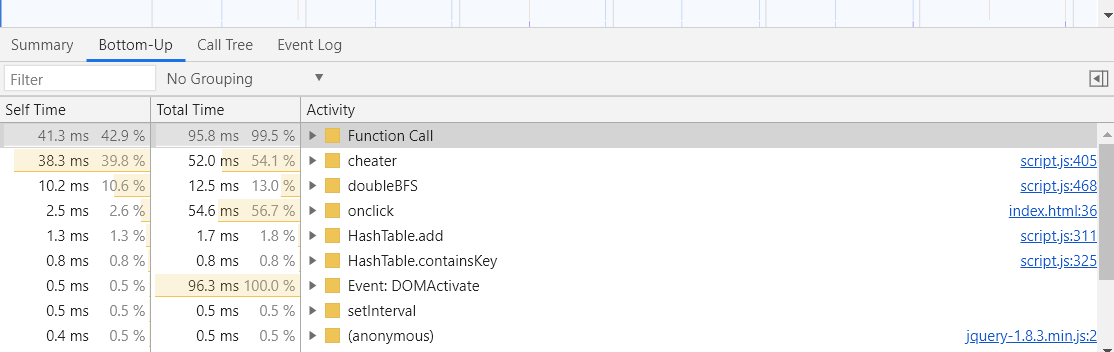
⑦改进思路
我们进行算法的改进。
1)可以将二维数组转化为数字而不是字符

2)优化循环
循环是编程中最常见的结构,优化循环是性能优化过程中很重要的一部分,通常采用倒序循环。

归根结底其实还是算法的问题
3)从普通广搜改为双向广搜。
假设单向BFS需要搜索 N 层才能到达终点,每层的判断量为 X,那么总的运算量为 X ^ NXN. 如果换成是双向BFS,前后各自需要搜索 N / 2 层,总运算量为 2 * X ^ {N / 2}2∗XN/2。如果 N 比较大且X 不为 1,则运算量相较于单向BFS可以大大减少,差不多可以减少到原来规模的根号的量级。
⑧性能分析图和程序中消耗最大的函数
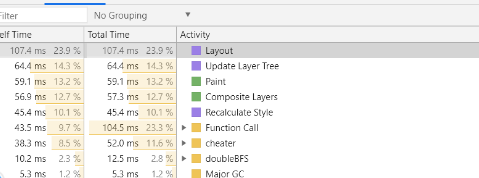
[2.2.2]Github的代码签入记录。
[2.2.3]遇到的困难及解决方法。
问题描述
(1)没有看清题目要求,博客要求随机抠掉一张图充当空格,我们只设计了扣掉最后一张
(2)没有考虑到网络接口的使用
(3)刚开始结队,由于学习速度不同而效率低下
解决尝试
(1)查阅了许多博客,及时更改
(2)我们互相让步,合理分工
是否解决
是
有何收获。
在分工的过程中,我们互相交流问题,给出意见和建议,受益匪浅。在合作的过程中学习和借鉴对方的思考方式,也克服了一个又一个困难,通过两个人合作来实现事半功倍的效果,两个人可以交流,交流可以使两个思维产生更多的灵感,不断的产生新想法来更好的解决问题。在本次作业前没有接触过前端的知识,所以刚开始有一点吃力,但在完成作业后学到了很多新知识,实践有助于对知识的理解,编程能力也有所加强,我们不仅学到了技术知识,而且更获得了许多宝贵的合作经验。
[2.2.4]评价你的队友。
太优秀了!!!编写代码能力很强
缺点就是太厉害了显得我很弱。。。
[2.2.5]提供此次结对作业的PSP和学习进度条
学习进度表:
| 第N周 | 新增代码(行) | 累计代码(行) | 本周学习耗时(小时) | 累计学习耗时(小时) | 重要成长 |
|---|---|---|---|---|---|
| 1 | 200 | 200 | 10 | 10 | 学习html,css |
| 2 | 400 | 600 | 12 | 22 | 学习javascript |
| 3 | 300 | 900 | 25 | 47 | 完成初步算法 |
| 4 | 250 | 1150 | 10 | 57 | 改进并完善算法 |
| PSP表格: | |||||
| PSP | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) | ||
| ---- | ---- | ---- | ---- | ||
| Planning | 计划 | 30 | 20 | ||
| Estimate | 估计这个任务需要多少时间 | 30 | 20 | ||
| Development | 开发 | 1200 | 1180 | ||
| Analysis | 需求分析 (包括学习新技术) | 420 | 420 | ||
| Design Spec | 生成设计文档 | 30 | 30 | ||
| Design Review | 设计复审 | 30 | 30 | ||
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 30 | 20 | ||
| Design | 具体设计 | 30 | 30 | ||
| Coding | 具体编码 | 420 | 420 | ||
| Code Review | 代码复审 | 90 | 80 | ||
| Test | 测试(自我测试,修改代码,提交修改) | 150 | 150 | ||
| Reporting | 报告 | 170 | 280 | ||
| Test Repor | 测试报告 | 120 | 200 | ||
| Size Measurement | 计算工作量 | 20 | 20 | ||
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 30 | 60 | ||
| Total | 合计 | 1400 | 1480 |
2.3原型设计最终实现效果页面:
1.点击重新开始按钮打乱图片,并且重置时间和步数

2.点击更换图片按钮,随机选择提供的无框字符文件夹里的图片拼图

3.点击动画展示按钮,在拼图区域上方显示最小步数和路线,并且以动画形式展示,中途玩家不可点击图片和按钮。
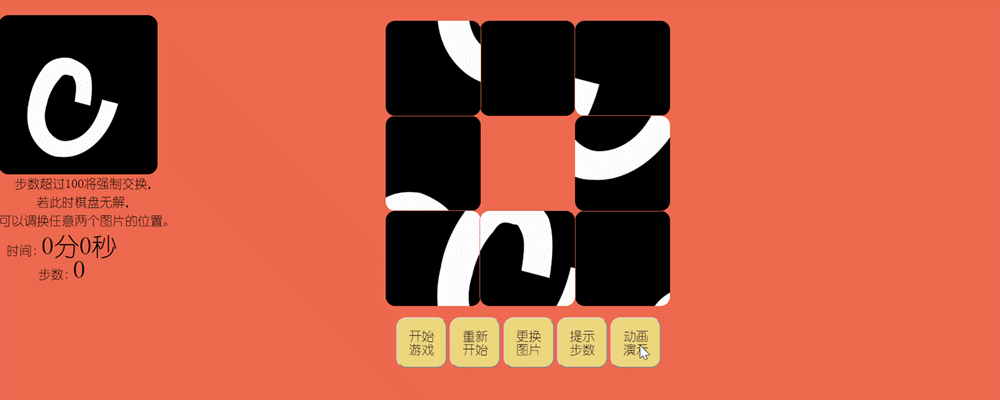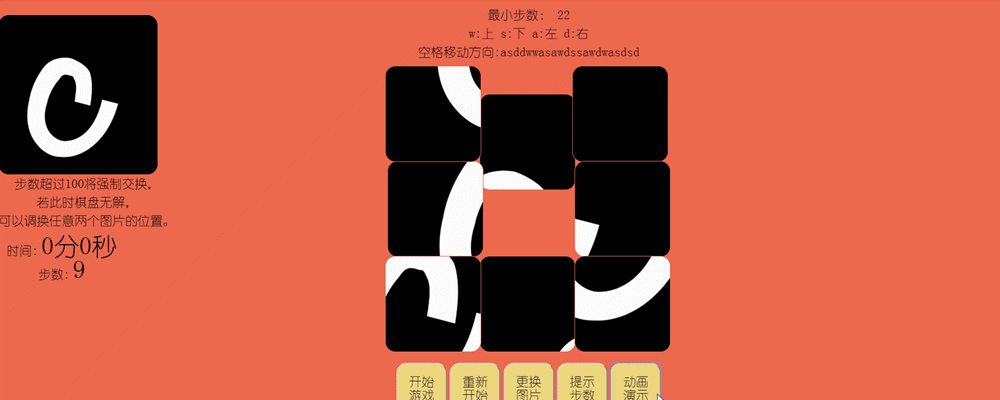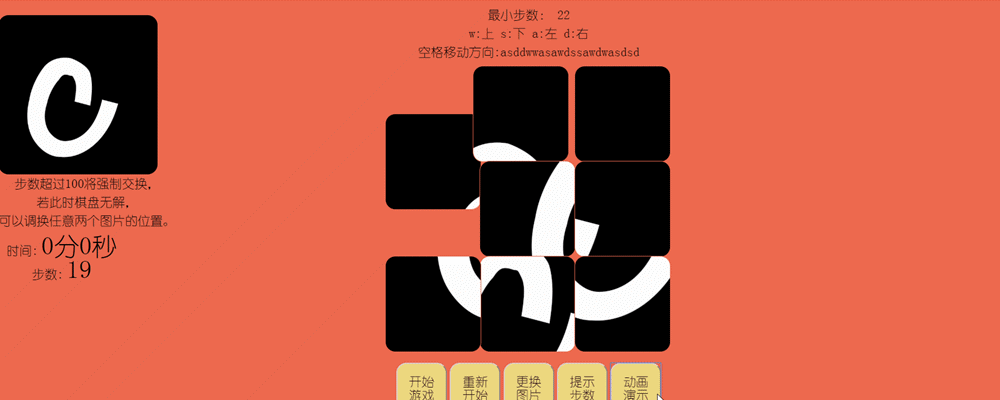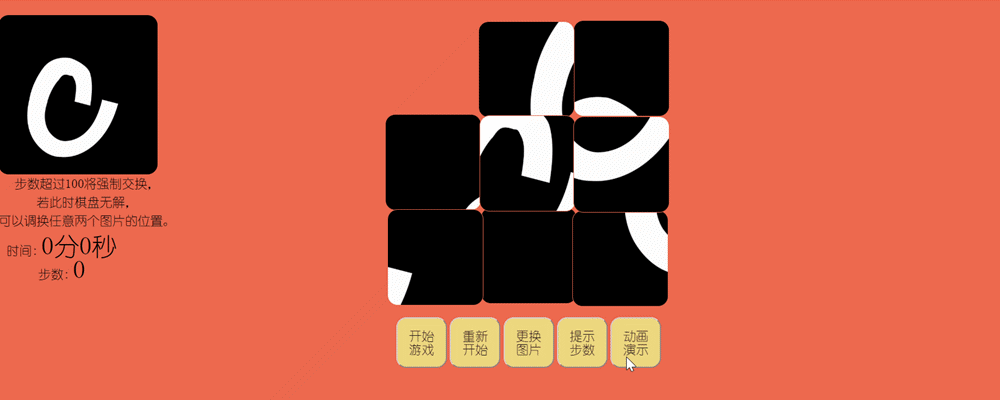
4.超过步数发生强制交换:当步数超过设定的值,将弹出步数超出弹出框,随机选择两块图片进行交换,并再次判断当前布局是否可解,若无解将在拼图区域上方出现输入栏供玩家输入要交换的两张图片序号,点击确定完成交换。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号