Codeforces 460 D. Little Victor and Set
暴力+构造
If r - l ≤ 4 we can all subsets of size not greater than k. Else, if k = 1, obviously that answer is l. If k = 2, answer is 1, because xor of numbers 2x and 2x + 1 equls 1. If k ≥ 4 answer is 0 because xor of to pairs with xor 1 is 0.
If k = 3, we can choose numbers 2x and 2x + 1 with xor 1. So we need to know, if we can get xor equals 0. Suppose that there are 3 such numbers x, y and z (r ≥ x > y > z ≥ l) with xor equals 0. Consider the most non-zero bit of numberx. At the same bit of y it's also 1, because xor equls 0, and y > z. Consider the next bit of numbers. If z have 0 there, we have to do next: set the previous bit of numbers x and y equals 0, and set current bit equals 1. Obviously xor still equals 0, z hadn't changed and numbers x and y stood closer to z, so they are still at [l, r].And x > y.Consider the next bit of numbers. If z has zero here than we will change most bits of x и y at the same way and so on. z > 0, so somewhen we will get to bit in which z has 1. Since xorequals 0, the same bit of x would be 1 because x > y, and y would have 0 there. At the next bits we will change bit in x to 0, and in numbers y and z to 1.Finally z would be greater or equal than before, and x would be less or greater than before, and x > y > z would be correct. So, we have the next: if such numbers x, y and z exist than also exist numbers:
1100…000
1011…111
0111…111
with xor equals 0. There are not much such triples, so we can check them.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long int LL;
LL L,R,K;
LL ans=0x3f3f3f3f3f3f3f3f;
int main()
{
cin>>L>>R>>K;
if(R-L+1<=4)
{
LL m=R-L+1;
LL sig=0;
for(LL i=1;i<(1LL<<m);i++)
{
LL temp=0;
LL wei=0;
LL si=i;
while(si)
{
wei++;
si=si&(si-1);
}
if(wei>K) continue;
for(LL j=0;j<m;j++)
{
if(i&(1LL<<j))
{
temp^=L+j;
}
}
if(temp<ans)
{
ans=temp;
sig=i;
}
}
cout<<ans<<endl;
LL wei=0;
LL tsig=sig;
while(tsig)
{
wei++;
tsig=tsig&(tsig-1);
}
cout<<wei<<endl;
for(LL i=0;i<m;i++)
{
if(sig&(1<<i))
{
cout<<L+i<<" ";
}
}
cout<<endl;
}
else
{
if(K==1)
{
cout<<L<<endl;
cout<<1<<endl;
cout<<L<<endl;
}
else if(K==2)
{
if(L%2) L++;
cout<<1<<endl;
cout<<2<<endl;
cout<<L<<" "<<L+1<<endl;
}
else if(K==3)
{
bool flag=false;
LL mx=3,mi=1;
while(mx<=R)
{
if(mi>=L)
{
flag=true;
cout<<0<<endl<<3<<endl;
cout<<mx<<" "<<mx-1<<" "<<mi<<endl;
break;
}
mx<<=1LL;
mi<<=1LL; mi++;
}
if(flag==false)
{
if(L%2) L++;
cout<<1<<endl;
cout<<2<<endl;
cout<<L<<" "<<L+1<<endl;
}
}
else
{
cout<<0<<endl;
cout<<4<<endl;
if(L%2) L++;
cout<<L<<" "<<L+1<<" "<<L+2<<" "<<L+3<<endl;
}
}
return 0;
}

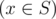 the
following inequality holds
the
following inequality holds 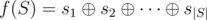 must
be as small as possible.
must
be as small as possible.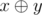 represents
the operation of bitwise exclusive OR. In other words, it is the XOR operation.
represents
the operation of bitwise exclusive OR. In other words, it is the XOR operation.
 浙公网安备 33010602011771号
浙公网安备 33010602011771号