数据结构——排序

排序

概述

分类

按存储介质分：

内部排序：数据量不大，数据在内存，无需内外存交换数据
外部排序：数据量较大，数据在外存（文件排序）

外部排序时，将数据分批调入内存，中间结果还要及时放入外存

按比较器个数

串行排序：单个处理机（同一时刻比较一对元素）
并行排序：多个处理器

按主要操作

比较排序：用比较的方法

插入排序，交换排序，选择排序，归并排序

基数排序：不比较元素的大小，仅仅根据元素本身的取值确定其有序位置

按辅助空间

原地排序：O（1），所占的辅助空间与参加排序的数据量大小无关
非原地

按稳定性：

稳定排序：能够使任何数值相等的元素，排序以后相对次序不变
非稳定排序

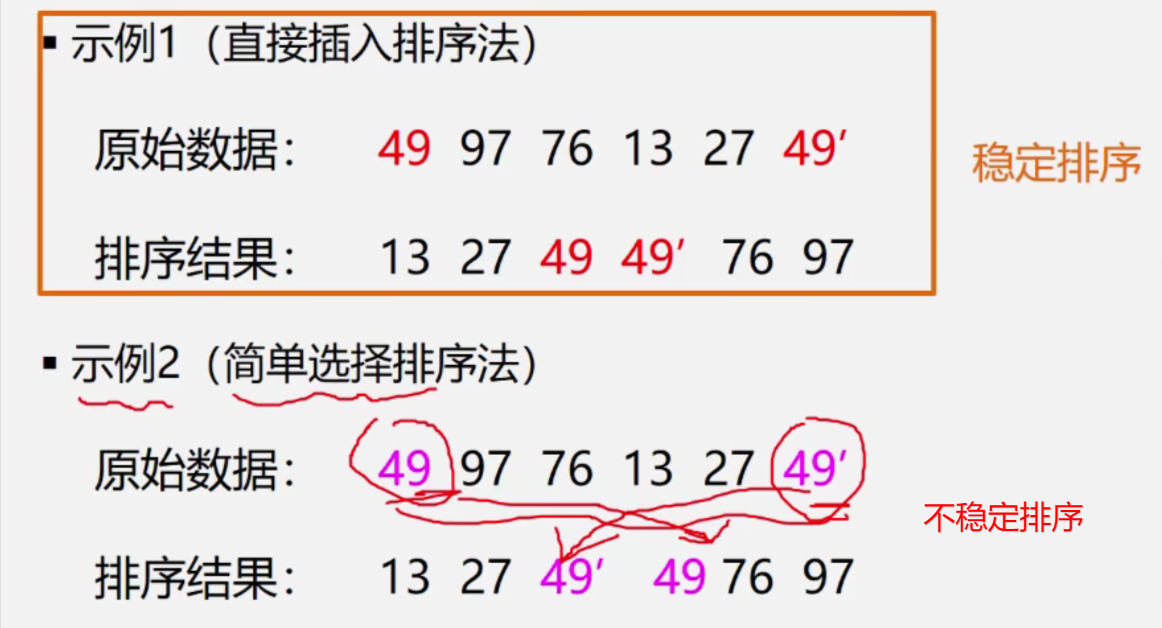
排序的稳定性只对结构类型的数据排序有意义

排序方法是否稳定，并不能衡量一个排序算法的优劣

例如

按自然性

自然排序：输入的数据越有序，排序的速度越快
非自然排序

# define MAXSIZE 20//设记录不超过20
typedef int KeyType;//设关键字类型为整型

typedef struct
{//定义每个记录的结构
    KeyType key;
    //其他数据项
}RedType//Record type
    
typedef struct
{//定义顺序表结构
    RedType r[MAXSIZE + 1];//存储顺序表的向量,r[0]一般做哨兵或缓冲区
    int length;
}SqList;

插入排序

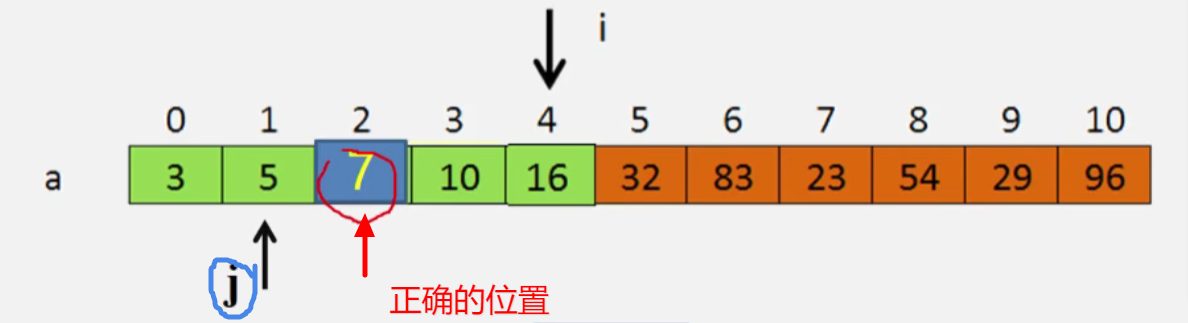
直接插入排序——顺序法定位插入位置

//复制插入元素到临时变量
x=a[i];
//前面的元素从后往前依次比较后按次序后移，查找插入位置(以从小到大举例)
for(j=i-1;j>=0&&x<a[j];j--)//一次循环比较两次
    a[j+1]=a[j];

//插入到该位置
a[j+1]=x;


//使用哨兵，另外如果待排元素已经比末尾数大，不排，直接插入到末尾（添加if）
//待排元素复制为哨兵
L.r[0]=L.r[i];
//记录后移，查找插入位置
for(j=i-1;L.r[0].key<L.r[j].key;--j)
    L.r[j+1]=L.r[j];
//插入到正确位置
L.r[j+1]=L.r[0];

算法

void InsertSort (SqList &L)
{
    int i,j;
    for(i=2;i<=L.length;i++)//从记录中第二个元素开始排
    {
        if(L.r[i].key<L.r[i-1].key)//左边末尾大了，执行插入排序
        {
            L.r[0]=L.r[i];
            for(j=i-1;L.r[0].key<L.r[j].key;j--)
                L.r[j+1]=L.r[j];//记录后移
            L.r[j+1]=L.r[0];
        }
    }
}

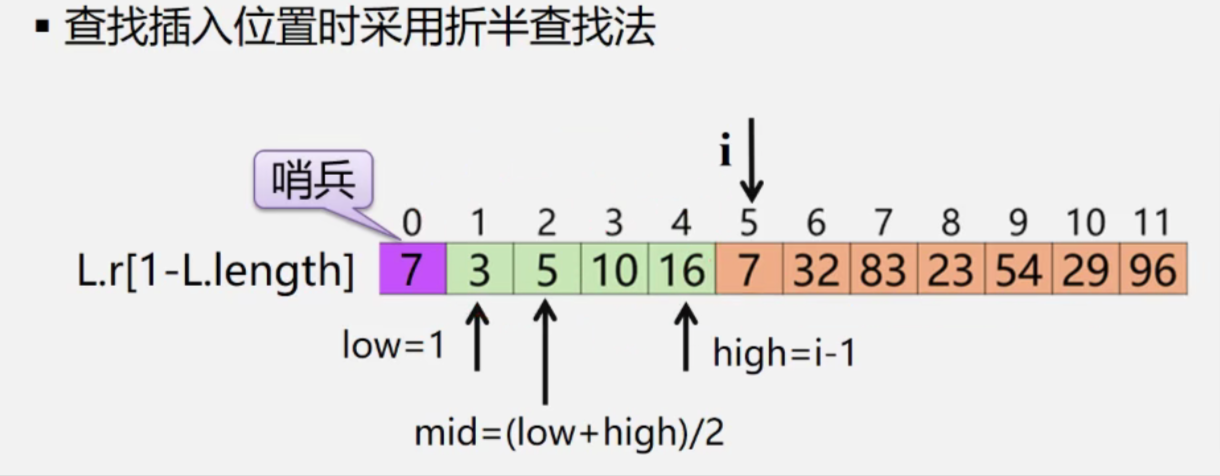
二分（折半）插入排序——前半区有序下二分法定位

算法

void BInsertSort(SqList &L)
{
    for(i=2;i<=L.length;++i)//依次插入第2~第n个元素
    {
        L.r[0]=L.r[i];//当前插入元素存到“哨兵位置”
        low=1;high=i-1
        while(low<=high) //二分查找插入位置
        { 
            mid=(low+high)/2;
            if(L.r[0].key<L.r[mid].key)  high =mid-1;   //左半区继续
            else low=mid+1;
            
            
        }//循环结束high+1则为插入位置;
        for(j=i-1;j>=high+1;--j) L.r[j+1]=L.r[j];//移动元素，空出high+1的位置
        L.r[high+1]=L.r[0];//插入到正确位置
    }
}//二分插入排序

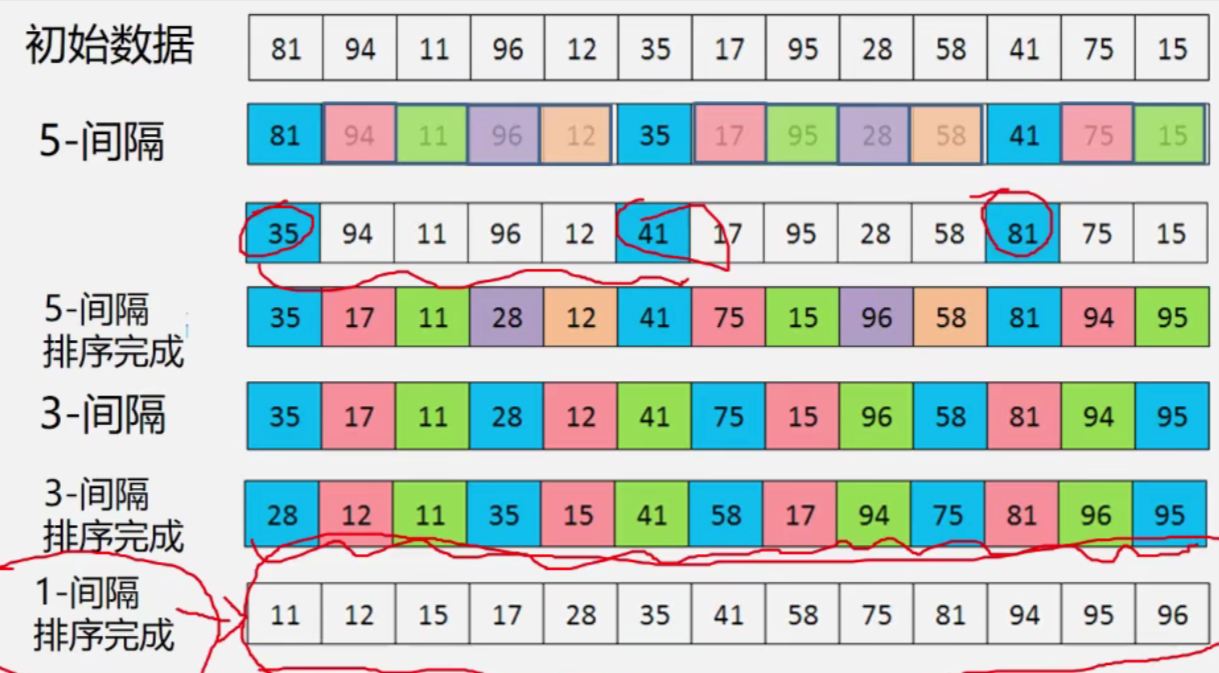
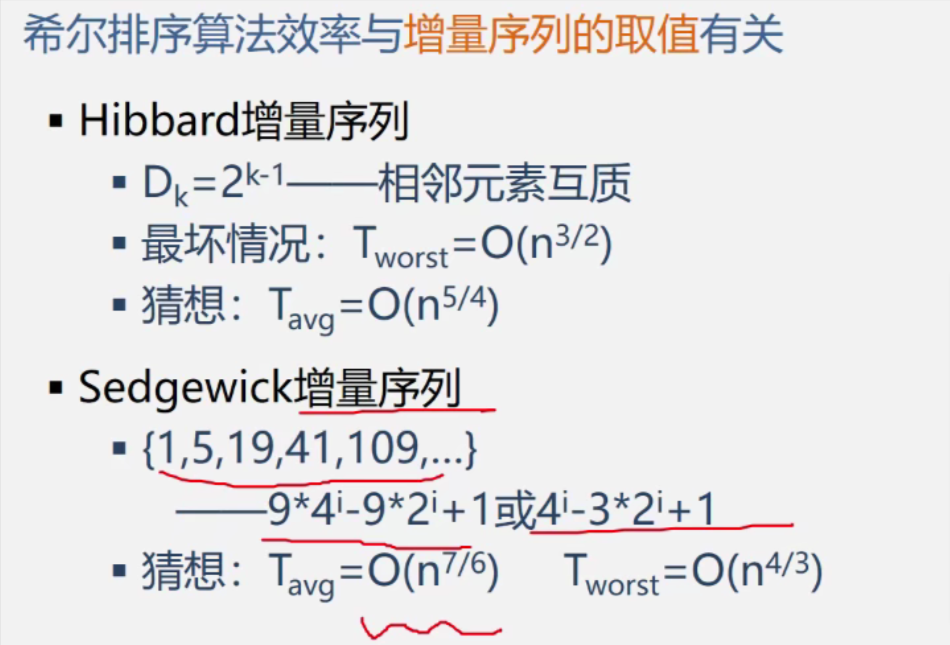
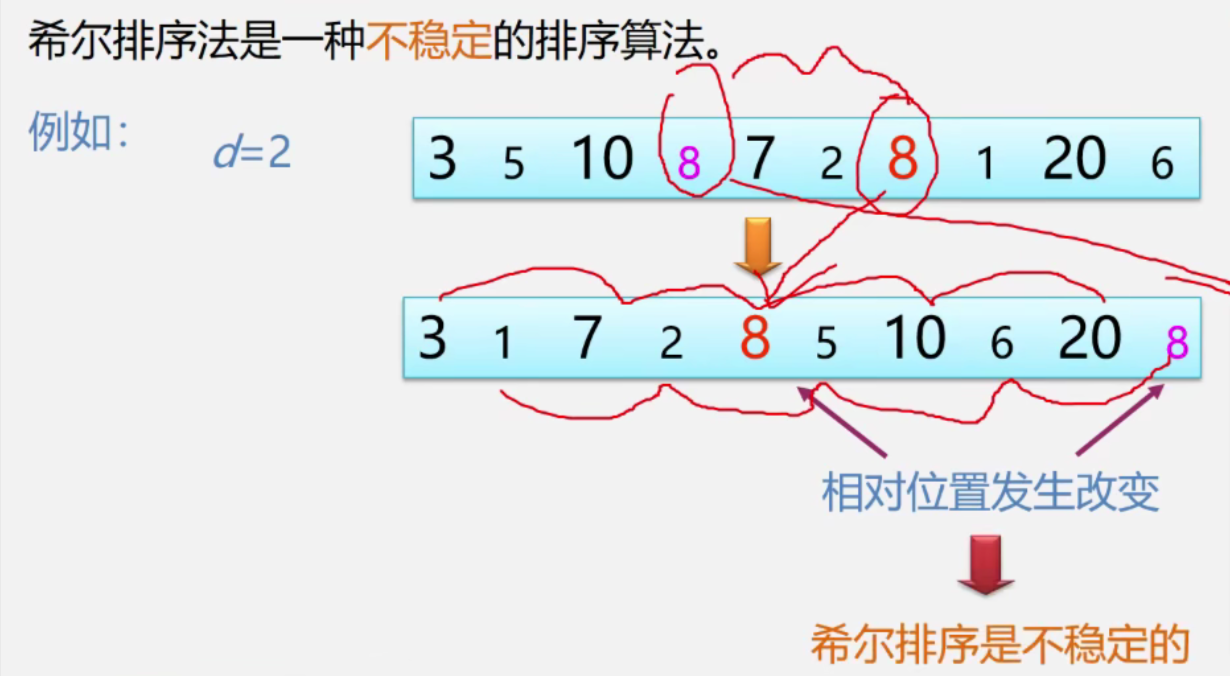
希尔排序——缩小增量多遍插入排序（不宜用在链式存储结构）

思路：

定义增量序列D（最后一个元素必为1，即进行直接插入排序）

比如D3=5，D2=3，D1=1(互质)

对每个Dk进行“Dk-间隔”插入排序（即以Dk为间隔的几个数取出来排序）
如此Dk递减进行排序得到最后结果

特点：

一次移动跳跃间隔大，接近排序后的最终位置

最后一次只需要少量移动

增量序列必须时递减的，最后一个必为1

增量序列应互质

算法

//按增量序列dlta[0..t-1]对顺序表L做希尔排序
void ShellSert(SqList&L,int dlta[],int t)
{
    for(k=0;k<t;k++)
        ShellSort(L,dlta[k]);//一趟增量为dlta[k]的插入排序,总共t趟
}

void ShellSert(SqList &L,int dk)
{
    for(i=dk+1;i<=L.length;++i)
    {
        if(r[i].key<r[i-dk].key)
        {
            r[0]=r[i];
            for(j=i-dk;j>0&&(r[0].key<r[j].key);j=j-dk)
                r[j+dk]=r[j];
            r[j+dk]=r[0];//其实是把之前的间隔1改为dk即可
        }
    }
}

交换排序

冒泡（气泡）排序

——基于简单交换思想

基本思想：每趟不断将记录两两比较，并按“前小后大”规则交换

n个记录元素，总共需要n-1趟

第m趟得到结果需要比较n-m次

算法

void bubble_sort(SqList &L)//冒泡排序算法
{
    int m,n,i,j;
    RedType x;//交换时的临时变量
    for(m=1;m<=n-1;m++)//总共n-1趟
    {
        for(i=1;i<=n-m;i++)//每趟需要n-m次交换
        {
            if (L.r[j].key>L.r[j+1].key)//发生逆序
                x=L.r[j];L.r[j]=L.r[j+1];L.r[j+1]=x;//交换
        }
    }//外层for
}

void bubble_sort(SqList &L)//提高效率，一旦某一趟 不发生 交换可以终止
{
    int m,n,i,j;int flag=1;RedType x;//flag作为是否交换的标记
    for(m=1;m=n-1&&flag==1;m++)
    {
        flag=0;//每趟初始标记置0
        for(i=1;i=m-n;i++)
        {
            if(L.r[i].key>L.r[i+1].key)//交换就置1,本趟没发生过交换就会保持为0，外层循环条件也不会满足，终止
            {
                flag=1;
                x=L.r[i];L.r[i]=L.r[i+1];L.r[i+1]=x;
            }
            
        }
    }
}

快速排序

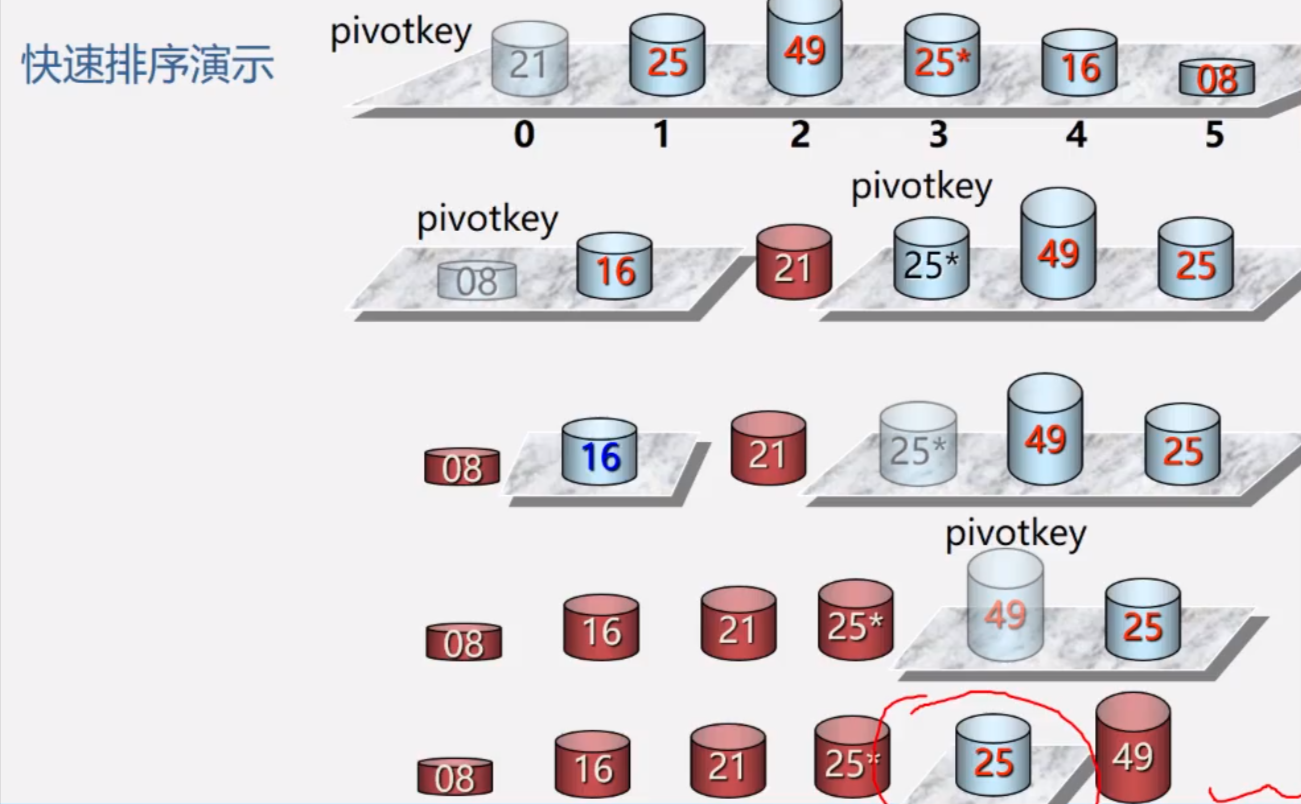
原理

实现：选定一个中间数（可以是第一个数，最后一个数，最中间的数，任选一个数）作为参考，所有元素与之比较，小的调到左边，大的调到右边

越乱越快，反倒不适合有序序列的排序。所以快排不是自然排序方法

void main()
{
    QSort(L,1,L.length);
}

void QSort(SqList &L,int low,int high)
{
    if(low<high)//low,high未重合
    {
        center=Partiton(L,low,high);//找到排好序后中心元素该放的位置，将L一分为二，其中包含了交换操作
        QSort(L,low,center-1);//新左区间,对低子表递归排序
        QSort(L,center+1,high);//新右区间
    }
}

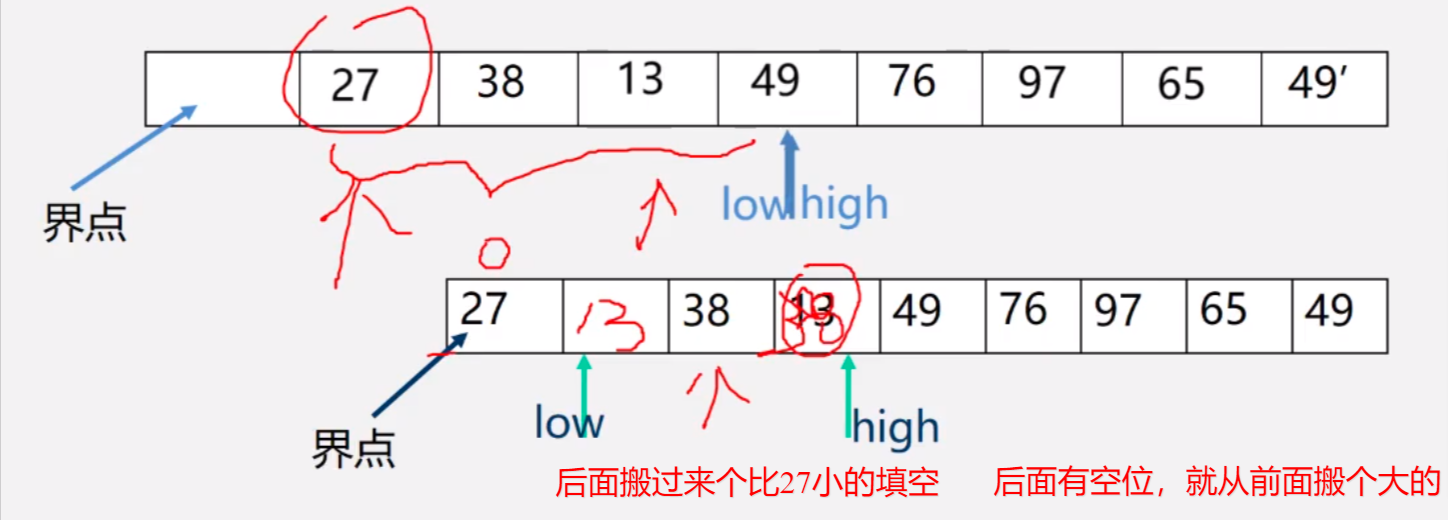
//找中心元素该放置的位置，把比中心点小的放前面，大的放后面
int Partition(SqList &L,int low,int high)
{
    L.r[0]=L.r[low];//复制给0号位，相当于空出low位
    center = L.r[low].key;//这里的center为中心元素的值大小
    while(low<high)
    {
        while(low<high&&L.r[high].key>=center) high--;
        L.r[low]=L.r[high];//把小于0号元素的拿到前面空位，产生后面空位
        while(low<high&&L.r[low].key<=center) low++;
        L.r[high]=L.r[low];//把大于0号元素的拿到后面空位，产生前面空位
    }
    L.r[low]=L.r[0];//找到中心元素该在的位置（空着），用0号元素填入
    return low;//返回该位置
}

时间复杂度，平均为O(nlog(2)n)
- 结果表明：就平均计算时间而言，快速排序是我们所讨论的所有内排序方法中最好的一个
空间复杂度

快速排序不是原地排序

由于程序使用了递归（调用系统栈），而栈长取决于递归调用的深度（即使不用递归，也需要用用户栈）

- 平均调用情况下要O(logn)的栈空间
稳定性：不稳定

选择排序

简单选择排序

基本操作：1. 从n个记录中找出关键字最小的记录，将它与第一个记录交换

2. 从剩余的n-1个记录中找出关键字次小的记录，将它与第二个记录交换

。。。。。。。

算法分析：其中比较次数：无论待排序列处于什么状态，选择排序所需进行的“比较”次数都相同

不稳定

void SelectSort(SqList &L)
{
    for(i=1;i<L.length;i++)//共进行n-1趟
    {
        k=i;//拟定初始最小值
        for(j=i+1;j<=L.length;j++)//从第i+1位开始依次待交换（其前面有序）
            if(L.r[j].key<L.r[k].key) k=j;//记录最小值位置
        if(k!=i) L.r[i]与L.r[k]; //交换
    }
}

堆排序

堆的定义

从堆的定义可以看出，堆实质是满足如下性质的完全二叉树（线性表）：二叉树中任一非叶子结点均小于（大于）它的孩子结点

堆排序的概念

若在输出堆顶的最小值（最大值）后，使得剩余n-1个元素的序列重新建成一个堆，再得到次小（次大）。。。

实现堆排序需解决两个问题

如何由一个无序序列建成一个堆
如何输出堆顶元素后，调整元素为一个新的堆

堆的调整（解决问题2）

建立堆（解决问题1）

堆排序算法

void HeapSort(elem R[])//对R[1]到R[n]进行堆排序
{
    int i;
    for(i =n/2;i>=1;i--)//建立初始堆
        HeapAdjust(R,i,n);
    for(i=n;i>1;i--)//进行n-1趟排序
    {
        Swap(R[1],R[i]);//根与最后一个元素交换（后面的元素为有序组）
        HeapAdjust(R,1,i-1);//对R[1]到R[i-1]重新建堆
    }
}

效率分析

类别	排序方法	时间复杂度			空间复杂度	稳定性
		最好	最坏	平均	辅助存储
插入排序	直接插入排序	O(n)	O(n^2)	O(n^2)	O(1)	稳定
	二分排序	差	优	O(n^2)	O(1)	稳定
	希尔排序	O(n)	O(n^2)	~O(n^1.3)	O(1)	不稳定
交换排序	冒泡排序	O(n)	O(n^2)	O(n^2)	O(1)	稳定
	快速排序	O(nlogn)	O(n^2)	O(nlogn)	O(nlogn)	不稳定
选择排序	简单选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	不稳定
	堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n^2)	不稳定
归并排序		O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定
基数排序		O(n+m)	O(k*(n+m))	O(k*(n+m))	O(n+m)	稳定

posted @ 2021-12-14 22:01 群青Bleu 阅读(88) 评论(0) 编辑收藏举报

刷新页面返回顶部

群青Bleu

数据结构——排序

排序

概述

分类

插入排序

直接插入排序——顺序法定位插入位置

二分（折半）插入排序——前半区有序下二分法定位

希尔排序——缩小增量多遍插入排序（不宜用在链式存储结构）

交换排序

冒泡（气泡）排序

快速排序

选择排序

简单选择排序

堆排序

堆的定义

堆排序的概念

实现堆排序需解决两个问题

堆的调整（解决问题2）

建立堆（解决问题1）

堆排序算法

效率分析

公告