9.13 校内模拟赛 题解报告
9.13 校内模拟赛 题解报告
扯
时隔许久的模拟赛...
T1 sb 树剖 话说怎么会考树剖啊
T2 搜索... 题意表述不清
T3 set 启发式合并... 完全没想到
大概这场考试就是这样...
关于考试过程以及一些题外话
读题
T1 好像是个 sb 题 分情况讨论一下好像可以做 但是显然是错的
T2 数据范围要么是搜索 要么状压 但是显然没读懂题
T3 看不出是什么题的神仙题
然后开始看 T1
"这不是随便求个 \(LCA\) 就能过"
码完 \(LCA\) 发现事情好像不太对劲
(又看了一遍题)
"负边??"
然后就先写了一个暴跳 再去弄正解...
发现维护一个最大值好像就能过 果断树剖 + 线段树
然后开始拍...
然后拍挂了...
然后开始调...
然后发现没有什么问题...
后来发现是那个暴跳写挂了...
拍上了 挂着 开 T2
T2 的题面极其诡异
写了个搜索 但是搜挂了
又感觉是不是要贪个枚举顺序 然后开始推式子 并没有什么软用
把 T3 暴力写了差不多到点了
白学了一天半的树启发 完全没想到是启发式合并...
得分情况
100 + 20 + 20 = 140
所以 T2 的搜索和 T3 的暴力并没有苟到多少分
题解
T1 小迟修马路
这个题一开始 BS 以为只需要判断一下 \(s\) 点与 \(a\) 点和 \(b\) 点的位置关系 然后直接把一整条路清掉 然后和 \(0\) 取个 \(\min\) 就好了 同时可以考虑把 \(s\) 当做整棵树的根 可以方便很多
后来想起来有负边 感觉不太对劲 就是大概会有这种情况:
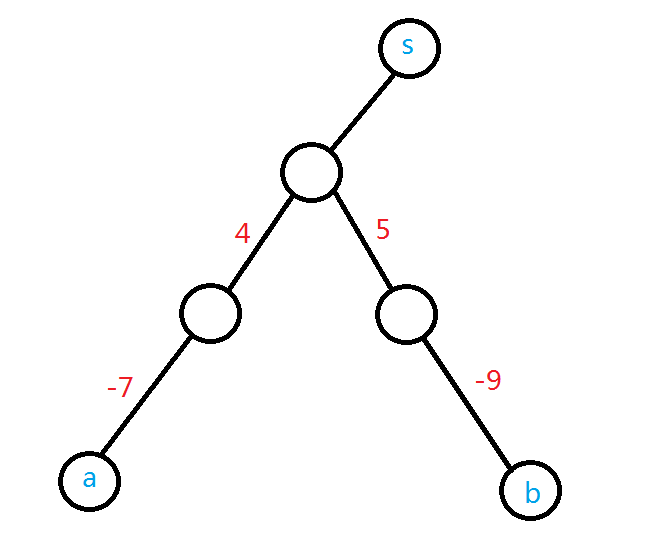
这张图中答案显然是 \(-12\)
所以问题在于各自找到 \(a\) 和 \(b\) 到 \(LCA_{a, b}\) 的路径上的一个点 \(x\) 使得 \(dis_{a, x}\) 最小且为负数
怎么找 路径的距离一定是差分求的 可以维护每个点到根节点的距离 写出来大概是这样:
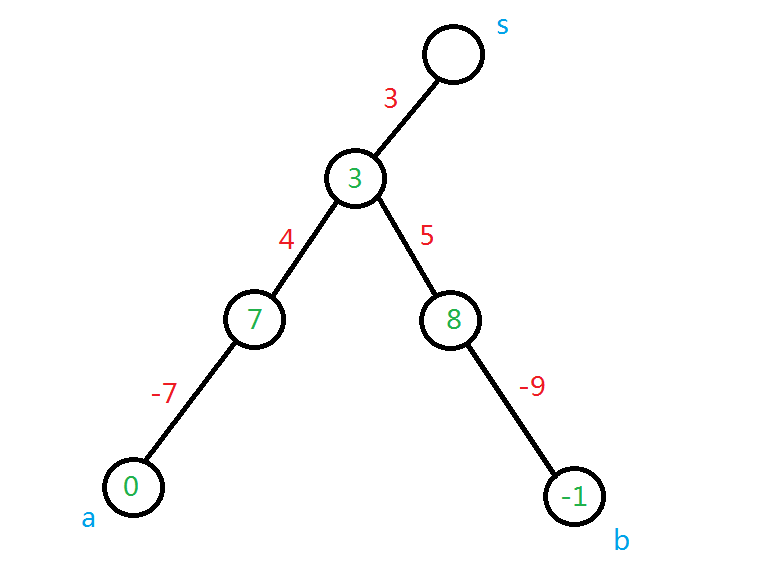
要找的点就是路径上到根节点距离最大的点
具体的至于为什么的话可以考虑差分求路径的过程
代码
/*
Source: road
有负边
a b 在 s 子树中: a b 两点到 lca 的路径中较大值 均为负值则不操作
a b 与 s 没关系: 同上一种
s 在 a 或 b 的子树中: 路径与 0 取 min
s 在 a 到 b 的路径上: a 到 s 与 b 到 s 的路径中较大的与 0 取 min
可以直接把 s 当根就没这些事了
直接考虑 a b 的 lca 即可
有点问题... 有负边
考虑开始消去的位置
首先有个暴跳的暴力
把每个点到根的距离看做这个点的点权 树剖维护路径点权最大值以及最大值的点的编号
一个半小时 拍上了
*/
#include<cstdio>
#include<cstring>
#define int long long
#define pt putchar(' ')
#define pn putchar('\n')
#define Abs(x) ((x) < 0 ? -(x) : (x))
#define Max(x, y) ((x) > (y) ? (x) : (y))
#define Min(x, y) ((x) < (y) ? (x) : (y))
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*----------------------------------------------------------*/
const int A = 1e4 + 7;
const int B = 2e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
/*----------------------------------------------------------*/
inline void File() {
freopen("road.in", "r", stdin);
freopen("road.out", "w", stdout);
}
/*----------------------------------------------------------*/
int n, q, s, fa[B], dep[B], dis[B], pos[B];
struct edge {int v, w, nxt;} e[B << 1];
int head[B], ecnt;
/*----------------------------------------------------------*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
void Print(int x) {if(x < 0) putchar('-'), x = -x; if(x > 9) Print(x / 10); putchar(x % 10 ^ 48);}
/*----------------------------------------------------------*/
void add_edge(int u, int v, int w) {e[++ecnt] = (edge){v, w, head[u]}; head[u] = ecnt;}
namespace Seg {
#define ls(x) x << 1
#define rs(x) x << 1 | 1
#define mid (t[p].l + t[p].r >> 1)
struct node {
int l, r, max, id;
node() {l = r = id = 0; max = -INF;}
} t[B << 2];
node operator + (node x, node y) {
node z; z.l = x.l; z.r = y.r;
if(x.max > y.max) z.max = x.max, z.id = x.id;
else z.max = y.max, z.id = y.id;
return z;
}
void build(int p, int l, int r) {
t[p].l = l; t[p].r = r; if(l == r) {t[p].max = dis[pos[l]]; t[p].id = pos[l]; return ;}
build(ls(p), l, mid); build(rs(p), mid + 1, r); t[p] = t[ls(p)] + t[rs(p)];
}
node query(int p, int l, int r) {
if(l <= t[p].l && t[p].r <= r) return t[p];
if(l <= mid) if(r > mid) return query(ls(p), l, r) + query(rs(p), l, r);
else return query(ls(p), l, r); else return query(rs(p), l, r);
}
}
namespace Cut {
int siz[B], son[B], top[B], dfn[B], kcnt;
void dfs1(int u, int pre) {
siz[u] = 1; fa[u] = pre; dep[u] = dep[pre] + 1;
for(int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v, w = e[i].w;
if(v == pre) continue;
dis[v] = dis[u] + w; dfs1(v, u); siz[u] += siz[v];
if(!son[u] || siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp; dfn[u] = ++kcnt; pos[kcnt] = u;
if(!son[u]) return ; dfs2(son[u], tp);
for(int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v; if(v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
int LCA(int x, int y) {
while(top[x] != top[y])
{
if(dep[top[x]] < dep[top[y]]) Swap(x, y);
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
int query(int x, int y) {
Seg::node res;
while(top[x] != top[y])
{
if(dep[top[x]] < dep[top[y]]) Swap(x, y);
res = res + Seg::query(1, dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if(dfn[x] > dfn[y]) Swap(x, y);
res = res + Seg::query(1, dfn[x], dfn[y]);
return res.id;
}
}
void work1() {
for(int i = 1; i ^ q + 1; ++i)
{
int x = read(), y = read(), z = Cut::LCA(x, y);
if(z == x || z == y)
{
if(dep[x] < dep[y]) Swap(x, y); int min = 0, tmp = x;
for(int j = x; j != fa[y]; j = fa[j])
if(dis[x] - dis[j] < min) min = dis[x] - dis[j], tmp = j;
Print(dis[x] - dis[tmp]); pn;
}
else
{
int min1 = 0, tmp1 = x, min2 = 0, tmp2 = y;
for(int j = x; j != fa[z]; j = fa[j])
if(dis[x] - dis[j] < min1) min1 = dis[x] - dis[j], tmp1 = j;
for(int j = y; j != fa[y]; j = fa[j])
if(dis[y] - dis[j] < min2) min2 = dis[y] - dis[j], tmp2 = j;
int res1 = dis[x] - dis[tmp1] + dis[y] - dis[z], res2 = dis[y] - dis[tmp2] + dis[x] - dis[z];
Print(Min(res1, res2)); pn;
}
}
}
void work2() {
for(int i = 1; i ^ q + 1; ++i)
{
int x = read(), y = read(), z = Cut::LCA(x, y);
if(x == y) Print(0), pn;
else if(z == x || z == y)
{
if(dep[x] < dep[y]) Swap(x, y);
int tmp = Cut::query(x, y);
Print(dis[x] - dis[tmp]); pn;
}
else
{
int tmp1 = Cut::query(x, z), tmp2 = Cut::query(y, z);
int res1 = dis[x] - dis[tmp1] + dis[y] - dis[z], res2 = dis[y] - dis[tmp2] + dis[x] - dis[z];
Print(Min(res1, res2)); pn;
}
}
}
void Main() {
File();
n = read(); q = read(); s = read();
for(int i = 1, x, y, z; i ^ n; ++i) x = read(), y = read(), z = read(), add_edge(x, y, z), add_edge(y, x, z);
Cut::dfs1(s, 0); Cut::dfs2(s, s); Seg::build(1, 1, n);
// if(n * q < D) work1();
// else work2();
work2();
}
/*----------------------------------------------------------*/
signed main() {Main(); return 0;}
T2 bride
题目表述难以理解 提出谴责
搜索
先搜 \(K\) 次减的机会给谁 再搜具体怎么投票
搜 \(K\) 的时候从上一个人开始搜 避免重复计算
然后注意亿些细节就能过
代码
/*
Source: bride
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#define pt putchar(' ')
#define pn putchar('\n')
#define Abs(x) ((x) < 0 ? -(x) : (x))
#define Max(x, y) ((x) > (y) ? (x) : (y))
#define Min(x, y) ((x) < (y) ? (x) : (y))
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*----------------------------------------------------------*/
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
/*----------------------------------------------------------*/
inline void File() {
freopen("bride.in", "r", stdin);
freopen("bride.out", "w", stdout);
}
/*----------------------------------------------------------*/
int n, K, A, w[10], h[10], p[10][110];
struct node {int w, h;} a[10];
bool vis[10];
double sum, ans = 1e9;
/*----------------------------------------------------------*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
void Print(int x) {if(x < 0) putchar('-'), x = -x; if(x > 9) Print(x / 10); putchar(x % 10 ^ 48);}
/*----------------------------------------------------------*/
double work(int s, int cnt) {
double res = 1;
if(cnt > n / 2) res = A * 1.0 / (A + s);
for(int i = 1; i ^ n + 1; ++i)
if(vis[i]) res *= Max(h[i], 0) * 1.0 / 100;
else res *= 1 - Max(h[i], 0) * 1.0 / 100;
return res;
}
void dfs2(int t, int cnt, int s) {
if(t == n + 1) {sum += work(s, cnt); return ;}
vis[t] = 1; dfs2(t + 1, cnt + 1, s + w[t]); vis[t] = 0; dfs2(t + 1, cnt, s);
}
void dfs1(int x, int last) {
sum = 0; dfs2(1, 0, 0); ans = Min(ans, 1 - sum);
if(!x) return ;
for(int i = last; i ^ n + 1; ++i) if(h[i] > 0)
{
h[i] -= 10;
dfs1(x - 1, i);
h[i] += 10;
}
}
void work1() {dfs1(K, 1); printf("%.6lf", ans);}
void Main() {
// File();
n = read(); K = read(); A = read();
for(int i = 1; i ^ n + 1; ++i) w[i] = read(), h[i] = read();
work1();
}
/*----------------------------------------------------------*/
signed main() {Main(); return 0;}
T3 爬山
set 启发式合并可以强过
复杂度 \(O(n \log^2 n)\)
代码
/*
Source: 爬山
*/
#include<set>
#include<cstdio>
#define pn putchar('\n')
#define IT std::set <int> :: iterator
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*----------------------------------------------------------*/
const int B = 1e5 + 7;
/*----------------------------------------------------------*/
int n, m, a[B], id[B], ans[B];
std::set <int> t[B];
/*----------------------------------------------------------*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
void Print(int x) {if(x < 0) putchar('-'), x = -x; if(x > 9) Print(x / 10); putchar(x % 10 ^ 48);}
/*----------------------------------------------------------*/
void merge(int x, int y) {
if(t[id[x]].size() > t[id[y]].size()) Swap(id[x], id[y]);
for(IT i = t[id[x]].begin(); i != t[id[x]].end(); ++i) t[id[y]].insert(*i);
}
void Main() {
n = read(); m = read();
for(int i = 2; i ^ n + 1; ++i) a[i] = read() + 1;
for(int i = 1; i ^ n + 1; ++i) id[i] = i;
for(int i = 1, x; i ^ m + 1; ++i) x = read(), t[id[x + 1]].insert(read());
for(int i = n; i; --i) {ans[i] = t[id[i]].size(); if(a[i]) merge(i, a[i]);}
for(int i = 1; i ^ n + 1; ++i) Print(ans[i]), pn;
}
/*----------------------------------------------------------*/
signed main() {Main(); return 0;}
正解的话
把图建出来 应该是一棵树的形式
考虑只有一种标记的时候
在每个点上打上加一的标记 对于一个点 如果其子树中的权值不为 \(0\) 则这个点也有标记
然后考虑多种标记的情况
标记的顺序不影响最终答案 可以对标记重新排序 将相同的标记放到一块处理
对于每一种标记 将需要打标记的点按照 \(dfs\) 序排序 依次打上加一的标记 除第一个点以外 每个点在打完加一标记之后再在自身与上一个打标记的点的 \(LCA\) 的位置打上减一标记 这样就保证了贡献不会算重
处理完所有标记后 遍历一遍树 统计节点的权值即为该点答案
感觉这个东西跑的也不比上面那个暴力快多少 这里求 \(LCA\) 的时候是用树剖实现的 不知道换成 RMQ 会不会快一点
代码
/*
Source: T200442 爬山
所谓正解
*/
#include<map>
#include<vector>
#include<cstdio>
#include<algorithm>
#define pn putchar('\n')
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*----------------------------------------------------------*/
const int B = 1e5 + 7;
/*----------------------------------------------------------*/
int n, m, rcnt, dfn[B], c[B];
struct edge {int v, nxt;} e[B];
int head[B], ecnt;
std::map <int, int> mp;
std::vector <int> a[B];
/*----------------------------------------------------------*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
void Print(int x) {if(x < 0) putchar('-'), x = -x; if(x > 9) Print(x / 10); putchar(x % 10 ^ 48);}
/*----------------------------------------------------------*/
void add_edge(int u, int v) {e[++ecnt] = (edge){v, head[u]}; head[u] = ecnt;}
namespace Cut {
int siz[B], dep[B], son[B], fa[B], top[B], kcnt;
void dfs1(int u, int pre) {
siz[u] = 1; fa[u] = pre; dep[u] = dep[pre] + 1;
for(int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v; dfs1(v, u); siz[u] += siz[v];
if(!son[u] || siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp; dfn[u] = ++kcnt; if(!son[u]) return ; dfs2(son[u], tp);
for(int i = head[u]; i; i = e[i].nxt) if(e[i].v != son[u]) dfs2(e[i].v, e[i].v);
}
int LCA(int x, int y) {
while(top[x] != top[y])
{
if(dep[top[x]] < dep[top[y]]) Swap(x, y);
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
}
bool cmp(int x, int y) {return dfn[x] < dfn[y];}
void dfs(int u) {for(int i = head[u], v; i; i = e[i].nxt) dfs(v = e[i].v), c[u] += c[v];}
void Main() {
n = read(); m = read();
for(int i = 2, x; i ^ n + 1; ++i) x = read() + 1, add_edge(x, i);
Cut::dfs1(1, 0); Cut::dfs2(1, 1);
for(int i = 1; i ^ m + 1; ++i)
{
int x = read() + 1, y = read();
if(!mp[y]) mp[y] = ++rcnt;
a[mp[y]].push_back(x);
}
for(int i = 1; i ^ rcnt + 1; ++i) std::sort(a[i].begin(), a[i].end(), cmp);
for(int i = 1; i ^ rcnt + 1; ++i)
{
int x = a[i][0]; c[x]++;
if(a[i].size() == 1) continue;
for(int j = 1, ed = a[i].size(); j ^ ed; ++j)
{
int y = a[i][j], z = Cut::LCA(x, y);
c[y]++; c[z]--; x = y;
}
}
dfs(1);
for(int i = 1; i ^ n + 1; ++i) Print(c[i]), pn;
}
/*----------------------------------------------------------*/
signed main() {Main(); return 0;}


