某 CF dp 题单

前言

按照难度排序之后顺着来的

诶诶是升序不是降序了

有的感觉不懂的或者太难的就跳过了...QAQ ~~蒟蒻本蒻~~

尽量的做到坚持更新吧

题目

1. CF213C Relay Race

一来一去太麻烦了不妨设为两条路线一起从起点移向终点

首先可以写出一个很显然的四维 $dp$ 直接表示两条线的位置

再看一下数据范围 $1 \leq n \leq 300$

嗯好空间起飞了

然后考虑怎样精简状态上面的状态表示的是两个点的横纵坐标这两个点一定是同时移动的也就是移动的步数一定是相同的考虑利用这一点对于一个点如果知道已经移动了多少步并且知道横纵坐标中的一个就可以求得另一个

所以不妨将状态设为三维

$f_{i, j, k}$ 表示移动了 $i$ 步后第一条路线所在的横坐标为 $j$ 第二条线所在的横坐标为 $k$ 时的最大收益

转移考虑移动的方向以及两个点是否重复可以比较简单的写出转移方程

最后的答案为 $f_{2n - 1, n, n}$ 一开始没想清楚直接上的 $2n$ 然后 $WA$ 一片

代码

2. CF119C Education Reform

不喜欢这道题一堆限制还要打印路径

写了一个很假的 $dp$ 样例都过不了...

然后就跑去看题解了

其实一开始的时候在犹豫那个 $c$ 有什么用题面看不太懂后来发现是用来排序的

记录学科的编号把相应的信息都记下来然后按照 $c$ 排序

状态: 设 $f_{i, j, k}$ 表示选了 $i$ 门学科到第 $j$ 天最后一门学科作业量为 $k$ 时的最大作业量

看一下数据 $a_i, b_i \leq 10^{16}$ 空间爆炸

但是题目中给了 $b_i - a_i \leq 100$

这就行了

状态: 设 $f_{i, j, k}$ 表示选了 $i$ 门学科到第 $j$ 天最后一门学科作业量为 $a_i + k$ 时的最大作业量

这样空间就能过了

转移考虑这一天的作业量是否合法与上一天转移过来的取较大值 (还是晕...

每进行一次转移的时候记录转移路径最后递归输出

注意 $c$ 有相等的情况转移的时候应该判掉

还要开 $long\ long$

~~话说每天的作业最大化是要闹哪样啊~~

烦

代码

3. CF353D Queue

其实做的时候一直感觉这是个贪...

每个女生最少一定要换前面男生个数次如果前面有女生最少要换前面女生个数加一次对于每一个两种情况取较大即可

为什么最少是女生个数加一次

考虑前面的女生是否相邻

不相邻的话两者之间必然隔了至少一个男生

相邻的话会被挡住

代码

4. CF837D Round Subset

总会遇到一些似鬼似仙的题目很诡异的一个 $dp$

首先要想到只有非零数末尾的零是有贡献的而这些零一定来自于 $2$ 和 $5$ 也就是说可以对于所取的数含有的因子 $2$ 和 $5$ 的个数进行 $dp$

~~然而但是我并没有想到甚至还想对末尾的零进行 dp 直到后来发现数据跟值域沾点边就飞升了~~

$dp$ 的前两维是比较容易确定的

$f_{i, j}$ 表示考虑到第 $i$ 个数选取了 $j$ 个

考虑对所选数中含因子 $2$ 和 $5$ 的个数进行 $dp$

$f_{i, j, a, b}$ 表示考虑到第 $i$ 个数选取了 $j$ 个数所选数中共包含 $a$ 个因子 $2$ 以及 $b$ 个因子 $5$ 这一状态是否可达

答案就是 $\max(\min(a, b))$

不用算复杂度就可以预感到四维的状态基本是要上天的但是 $dp$ 数组本身并没有用考虑把其中一维塞到数组里面

$f_{i, j, k}$ 表示考虑到第 $i$ 个数选取了 $j$ 个数所选数中共包含 $k$ 个因子 $2$ 时包含因子 $5$ 的数量

转移考虑每个数选与不选当成背包就可以了

注意数组第三维的大小大概开到 $6000$ 左右因子的个数

第一维和第二维都是 $200$ 的感觉空间还是有点紧张

第一维 $i$ 的转移只与 $i - 1$ 有关可以滚一下

注意开 $long\ long$

代码

5. CF796D Police Stations

一个混入 $dp$ 题单的广搜题...

看到题解里面好多人都说 $d$ 没有用... 输入保证了树合法那个 $d$ 好像确实没有用

直接将警局入队然后开始搜就可以了对搜到的点染色一条边的两边的点的颜色不同那这条边就是可以删掉的

代码

6. CF540D Bad Luck Island

感觉又是一个不是很难但是比较鬼畜的题目

三个数的比较小状态直接设三维没有问题

$f_{i, j, k}$ 表示三个种族剩余的人数分为为 $i, j, k$ 个时的概率

$f_{r, s, p}$ 自然是 $1$

$i \times j + j \times k + k \times i$ 是所有情况发生的概率转移考虑某一情况的发生

代码

7. CF527D Clique Problem

一道神仙构造题

对于两个点 $i, j$ 不妨设 $x_i < x_j$ 对于两点之间右边的条件即为 $x_j - x_j > w_i + w_j$ 将 $i$ 放到一边有:$$x_i - w_i > x_j + w_j$$

对于一个点覆盖的区间为 $[x_i - w_i, x_i + w_i]$ 设为 $[l_i, r_i]$ 上式可以化为 $$l_i > r_j$$ 相当于两个区间没有交点

如果将所有的点转化为线段那么所有没有交集的线段之间都是有边的所以问题相当于在数轴上取若干条线段使得所取的所有线段没有交集最大化所取线段的数量

比较显然的贪心按照线段右端点排序直接取即可

代码

8. CF478D Red-Green Towers

首先可以很自然的写出一个三维的 $dp$ 即

$f_{i, j, k}$ 表示搭 $i$ 层使用 $j$ 个红块 $k$ 个绿块的方案数

有了层数自然可以算出所用的总方块数量显然第三维是没有必要的

状态 : $f_{i, j}$ 表示搭 $i$ 层使用 $j$ 个红块的方案数

转移 : $f_{i, j} = f_{i - 1, j} + f_{i, j - i}$

考虑一下时空复杂度积木最多有 $4 \times 10^5$ 块若是搭 $h$ 层有: $$\frac {h \times (h + 1)}2 = r + g$$ 估一下大概九百到一千

感觉时间比较玄乎开了两秒好像也差不多空间的话显然 $f_i$ 的转移只与 $f_{i - 1}$ 有关可以直接滚掉一维

然后考虑答案的区间

$dp$ 数组的第二维已经限制了 $r$ 是合法的所以需要考虑 $g$ 是否足够

考虑只用 $g$ 有 $$\frac {h \times (h + 1)}2 = g$$ 也就是说 $r$ 最少需要使用 $\frac {h \times (h + 1)}2 - g$ 块在这个范围内统计答案即可

代码

9. CF505C Mr. Kitayuta, the Treasure Hunter

边界比较苟的一道 $dp$

很自然的一个状态是 $f_{i, j}$ 表示当前在 $i$ 上一步跳了 $j$ 时的宝藏数

看一下数据范围都在 $3 \times 10^4$ 数量级空间炸了

~~(空间: 我tm天天爆炸)~~

但是题目中给出每次跳的距离与上一次的浮动为 $c - 1, c, c + 1$ 假设每一步都与上一步发生浮动一共跳跃了 $x$ 步有 $$\frac {d \times (d + 2x)}2 = n$$

设 $d = 1, n = 3 \times 10^4$ 算出的 $x$ 大概为三百左右但是不到

这样我们可以将状态改为

$f_{i, j}$ 表示当前在 $i$ 位置上一步跳了 $d + j$ 时的宝藏数

这样空间就没有问题了

但是很明显 $j$ 是有负数的所以需要全部加上一个常数调整下标

转移考虑上一次的位置及跳跃距离即可

代码

10. CF547B Mike and Feet

混入 $dp$ 题单的单调栈

对于每一长度的区间最大化区间中的最小值

在一段区间中的最小值是固定的设为 $a_i$ 将这种极大区间称为 $a_i$ 的控制范围

显然若 $a_i$ 控制的区间为 $[l_i, r_i]$ 那么对于所有区间长度为 $[1, r_i - l_i + 1]$ 的区间都可以做出贡献

对每一个数处理出其控制的区间贡献到其所能贡献的最大的区间长度上对于贡献到同一位置的答案取最大值再从 $n$ 逆向推回来对于每一长度的区间在能取的答案中取最大值即可

代码

11. CF1271D Portals

好题

做法非常多的一道题

首先需要明确一点对于一个城堡一定是在能占领它的最晚的时间使用 $1$ 的兵力进行占领是最优的

正确性也很显然任意时间占领的贡献是一样的早占领还有可能导致后面的兵力不足

所以对于每个点只需要保留其最后能够占领的时间即可

解法 $1$

很自然的一个 $dp$ 状态:

$f_{i, j}$ 表示当前在 $i$ 个城堡剩余 $j$ 个士兵时的最大收益

数据范围最大是 $5000$ 完全没有问题

转移:

在任意时刻 $$f_{i, j} = \max(f_{i - 1, j - b_i})$$

如果当前为某一城堡最后可以占领的时刻 $$f_{i, j} = \max(f_{i, j + 1})$$

转移的格式比较诡异统一一下刷表

\[f_{i, j + b_i} = \max(f_{i - 1, j}) \]

\[f_{i, j} = \max(f_{i, j + 1}) \]

答案为 $\max(f_{n, i})$

复杂度 $O(n^2)$

代码

解法 $2$

总兵力以及每个城堡需要和补充的兵力都是有的不妨将所有的城堡都打下来再考虑占领

首先在打的过程中兵力不够了自然是不合法的因为现在还没有考虑占领的问题

都打完之后呢

我们可以从大到小的贪心的占领城堡

为什么

因为一个城堡只需要 $1$ 的兵力不存在空下某一较大的收益而得到其他更大收益的情况

反正花费都是一样的我为什么不占收益大的

所以直接贪心的考虑每一座城堡

考虑在某一时刻占领每一座城堡占领的时刻一定是这个城堡可以占领的最后时刻在这一时刻占领一座城堡就会影响后面的操作相当于在之后攻打所有城堡时所能使用的兵力减一

我们可以记录一个数组为攻打该城堡的余俗兵力对某一时刻 $t$ 当 $t$ 时刻到 $n$ 时刻的余俗兵力的最小值大于 $0$ 时这一座城堡是可以占领的将这一城堡的贡献累加下来对于 $t$ 到 $n$ 时刻的余俗兵力减一

区间加区间最小值线段树可以直接维护

复杂度 $O(n\log n)$

代码

解法 $3$

可以直接贪吗?

对于每一座城堡在最后的时间之间占下来到兵不够的时候再说

那真到了兵不够的时候怎么办

找一个收益最少的地方把这里吐出来把兵腾出来继续打

为什么

首先要能打下来所以当然可以吐占哪不是占花费都一样为啥不占大的把小的空出来

维护一个最小值可以通过优先队列实现把占领的点扔进去吐的时候取最小的吐就行了

不合法的状态自然就是把地吐干净了依旧不够或者最后打完了兵成了负的还得吐

代码

上面那个解法三相当于为贪心提供了一个反悔的机会也是属于一类问题反悔贪心

有关的题目

CF865D Buy Low Sell High

P1792 [国家集训队]种树

12. CF1265E Beautiful Mirrors

期望 dp

设 $f_i$ 表示问第 $i$ 个镜子时还需要问的期望天数

有 $f_{n + 1} = 0$

$f_1$ 即为答案

转移:

\[f_i = \frac {p_i}{100}(f_{i + 1} + 1) + \left(1 - \frac {p_i}{100}\right)(f_1 + 1) \]

然后顺着上面那个东西倒着推化简过程太麻烦略去了

\[f_n = f_1 - \frac {p_n}{100}f_1 + 1\\ f_{n - 1} = f_1 - \frac {p_n}{100}\frac{p_{n - 1}}{100}f_1 + 1 + \frac {p_{n - 1}}{100}\\ f_{n - 2} = f_1 - \frac {p_n}{100} \frac {p_{n - 1}}{100} \frac {p_{n - 2}}{100} f_1 + 1 + \frac {p_{n - 1}}{100} \frac {p_{n - 2}}{100} + \frac {p_{n - 2}}{100}\\ f_{n - 3} = f_1 - \frac {p_n}{100} \frac {p_{n - 1}}{100} \frac {p_{n - 2}}{100} \frac {p_{n - 3}}{100} f_1 + 1 + \frac {p_{n - 1}}{100} \frac {p_{n - 2}}{100} \frac {p_{n - 3}}{100} + \frac {p_{n - 2}}{100} \frac {p_{n - 3}}{100} + \frac {p_{n - 3}}{100} \]

整理一下大概式子就有了:

\[f_i = f_1 - \prod_{j = i}^n \frac {p_j}{100}f_1 + \sum_{j = i}^{n - 1}\prod_{k = i}^j \frac {p_k}{100} + 1 \]

把 $f_1$ 带进去得:

\[f_1 = f_1 - \prod_{i = 1}^n \frac {p_i}{100}f_1 + \sum_{i = 1}^{n - 1} \prod_{j = 1}^i \frac {p_j}{100} + 1 \]

再化简得到:

\[\prod_{i = 1}^n \frac {p_i}{100} f_1 = \sum_{i = 1}^{n - 1} \prod_{j = 1}^i \frac {p_j}{100} + 1 \]

那么答案就有了

\[ans = \frac {\sum_{i = 1}^{n - 1} \prod_{j = 1}^i \frac {p_j}{100} + 1}{\prod_{i = 1}^n \frac {p_i}{100}} \]

然后稍微处理一个前缀积处理一个逆元再对前缀积处理一个前缀和即可

代码

13. CF1271E Common Number

手玩题

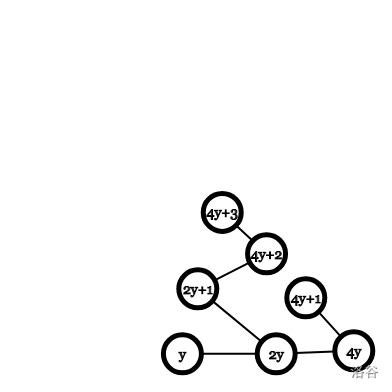
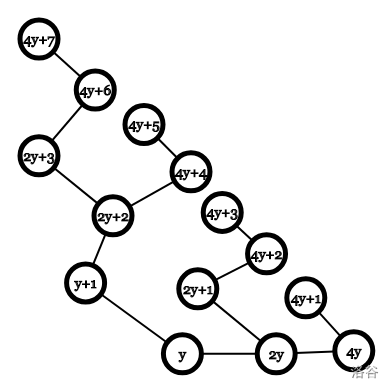
(图片来自题解)

上面是奇数的情况下面是偶数的情况

显然路径个数时可以直接统计的分奇偶二分即可

代码

14. CF16E Fish

状压 dp + 概率 dp

比较好想的一个 dp

看到 $n$ 的范围大概就知道是状压了

状态: 设 $f_S$ 表示存活的鱼的状态为 $S$ 的概率这里用 $0$ 表示存活设 $cnt_S$ 表示鱼的存活状态为 $S$ 时鱼的数量

转移:

\[f_{1 << i | S} = \frac {f_S \times a_{j, i}}{cnt_S \choose 2} \]

代码

15. CF768D Jon and Orbs

期望 dp

状态: 设 $f_{i, j}$ 表示取 $i$ 次取出 $j$ 个物品的期望次数

转移:

\[f_{i, j} = f_{i - 1, j - 1} \times \frac {n - j + 1}n + f_{i - 1, j} \times \frac jn \]

然后对于每个询问直接二分即可

代码

16. CF621E Wet Shark and Blocks

矩阵快速幂

根本想不到... 第一次见这种题...

首先有状态: $f_{i, j}$ 表示前 $i$ 个格子取的数余数为 $j$ 的方案数

其次有转移:

\[f_{i + 1, 10 \times j + k} = \sum f_{i, j} \times cnt_k \]

然后这个 dp 的第一维是 $10^9$ 的

所有的格子是一样的每一层向下一层的转移也相同类比矩阵快速幂求图中边权为 $1$ 长度为 $k$ 的路径条数

构造矩阵 $A$ 其中 $A_{i, j}$ 表示由 $i$ 转移到 $j$ 的方案数

设 $B = A^b$ 答案为 $B_{0, k}$

代码

17. CF235B Let's Play Osu!

期望 dp

比较简单了

状态:

设 $f_i$ 表示第 $i$ 次点击之后的期望得分

设 $g_i$ 表示第 $i$ 次点击之后的期望连续的 $O$ 的长度

转移:

\[f_i = (f_{i - 1} + (g_{i - 1} + 1)^2 - g_{i - 1}^2) \times p_i + f_{i - 1} \times (1 - p_i)\\ g_i = (g_{i - 1} + 1) \times p_i \]

每个状态只与上一个有关所以连数组都不用开注意一下转移顺序直接做即可

代码

18. CF351B Jeff and Furik

???

傻了.. 毫无头绪

结论题...

题目相当于求使得逆序对的个数为 $0$ 的期望操作次数

jeff 的操作必然减少一个逆序对 furik 的操作有一半的概率增加一个逆序对有一半的概率减少一个逆序对

所以每两次操作会各有一半的概率使逆序对减少二或者不变则每两次操作会使得期望逆序对数量减少一

然后答案就有了

分奇偶讨论一下奇数的话第一次操作的时候先减一再统计答案即可

代码

19. CF27E Number With The Given Amount Of Divisors

数论 + 搜索

引理: 对于唯一分解式形如 $x = p_1^{c_1}p_2^{c_2}\dots p_k^{c_k}$ 的数字 $x$ 其因数个数为 $\prod(c_i + 1)$

定理: 考虑一个因数为 $n$ 的最小整数 $x$ 则它的唯一分解式 $x = p_1^{c_1}p_2^{c_2}\dots p_k^{c_k}$ 中不妨设 $p_1 < p_2 < \dots < p_k$ 则一定满足: $p_1 = 2$ 且 $\forall i > 1, p_i$ 是大于 $p_{i - 1}$ 的第一个质数同时 $\forall i \in [1, k), c_i < c_{i + 1}$

然后 $2$ 的 $64$ 次方已经超过 $10^{18}$ 质数最多为 $64$ 前 $15$ 个质数连乘已经大于 $10^{18}$ 质数最多十五个然后就可以直接搜了

代码