Codeforces Round 736 div2
Codeforces Round 736 div2
前言
多测不清空 罚时两行泪
还有 这喵的翻译好难用啊
题目
A. Gregor and Cryptography
题意
给定一个素数 \(P\) 找到 \(a, b\) 使 \(p \% a = p \% b\)
多组数据
\(5 \leq p \leq 10^9, 1 \leq t \leq 10^3\)
题解
输出 \(2\) 和 \(p - 1\) 即可
正确性比较显然
但是比赛的时候并没有想到 只是 \(yy\) 了一下 感觉 \(p\) 为素数 符合的数一定不会太大 开个 \(map\) 记了一下余数 直接暴力枚举两个数去模 在某一个余数第二次出现的时候把这个连同上一个一块打出来 于是水了过去
然后 \(map\) 忘记清空... \(A\) 题吃罚
B. Gregor and the Pawn Game
题意
棋盘上下两侧各有对方和我方的若干棋子 对方棋子不移动 问我方棋子有多少能过到达对侧
棋子移动:
当正上方没有对方棋子时 可以向正上方移动
当左上方/右上方有多方棋子时 可以移去对方棋子并移动到左上方/右上方
多组数据
\(1 \leq t \leq 2 \times 10^4, 2 \leq n \leq 2 \times 10^5\)
题解
一个棋子可能到达的位置 没有棋子的正上方 有棋子的左上方或右上方 建图 二分图最大匹配
复杂度 \(O(n\sqrt n)\)
话说这复杂度真的能过吗...
然后比赛的时候并没有想到上边那个东西 然后意会了一下 感觉贪心好像也没什么问题 从左往右贪 优先向上 然后左 再然后右 把用过的地方标记一下 然后就过了 并没有被卡掉
然后标记数组忘记清空 \(B\) 题再次吃罚
所谓意会
能往上走一定往上走 因为能往上走上面一定是没有棋子的 其他位置的棋子一定不会过来 白给的地方 不用白不用
不能往上走的时候 正上方是有棋子的 优先考虑向左 若能去则去 因为从左往右扫 左上方的格子不会再被考虑到 这次占用后答案一定不会变劣 其次考虑向右 这时可能会挤掉右边间隔一个的位置的棋子 但是可以发现 不断向右挤过去 最后最多只会有一个棋子被挤下去 那么就算这个棋子不放 使得被挤下去的棋子有处可去 答案也就那样了
所以在我看来这个贪心没有什么问题
复杂度 \(O(n)\)
但是加上多组数据 我还是感觉这复杂度有点问题...
C. Web of Lies
题意
给定 \(n\) 个点 \(m\) 条边的图 \(q\) 次操作
\(1\ u\ v\) 新建一条边 \(u \to v\)
\(2\ u\ v\) 删去一条边 \(u \to v\)
\(3\) 查询
对于查询 若一个点有连向其他点的边 且连接的所有点的编号均大于该点 该点删去 不断重复 直到不满足条件
询问之间相互独立
\(1 \leq n \leq 2 \times 10^5, 0 \leq m \leq 2 \times 10^5\)
题解
官方的题解就算了(看不懂英文
写一下自己的做法
发现其实就是求连通块个数... 但是很难做 考虑找其他的性质
手玩一下 删边的时候在每一个连通块里面都是从小往大删的 最小的点率先被删 其他次小的点因为最小的点被删而被删 不难想象一个连通块中只会剩下最大的点 也可以进一步的得出 一个点只要连向比它编号大的点就会被删 我们可以直接在修改时维护一个点连线编号比他大的点的数量 顺便维护答案即可
就是正解了 和题解也差不多了
赛时 sb 的弄了个并查集考虑联通情况 后来发现题目保证了...(顺便吼了一句误导了一机房的人... 导致一众仙人卡在 C
我道歉 虽然没有用就是了(逃
所以不要听我的就是了
D. Integers Have Friends
题意
给定长为 \(n\) 的序列 求最长的区间长度 使区间中所有数模 \(m\) 同余
多组数据
\(1 \leq t \leq 2 \times 10^4, 1 \leq n \leq 2 \times 10 ^ 5, 1 \leq a_i \leq 10^{18}\)
扯
猜到了一半的结论 但是还是不会/kk
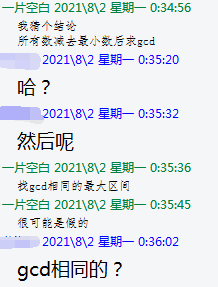
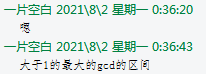
所以这结论果然是假的
题解
构造差分序列 设 \(d_i = abs(a_{i + 1} - a_i)\) 将问题转化为 \(\gcd\) 问题
求一个最大区间 其 \(\gcd\) 大于 \(1\)
线段树或者 st 表维护
不要乱写 memset 多组数据卡到 \(T\) 飞(我也就交了个十遍
E. The Three Little Pigs**
题意
给定 \(n, q\) 对于每个 \(q\) 给定 \(k\) 求:$$\sum_{i = 1}^n{3i \choose k} \times [k \geq 3i]$$
\(1 \leq n \leq 10^6, 1 \leq q \leq 10^5\)
扯
题意简述就是题目中所有我能看出来的东西了...
E 不会 跑路了 也不知道上面总结的那个题面对不对


