$NOIP\ 2018\ Day2$ 模拟考试 题解报告
\(NOIP\ 2018\ Day2\) 模拟考试 题解报告
得分情况
\(T1\) \(84\ Pts\)
\(T2\) \(15\ Pts\)
\(T3\) \(44\ Pts\)
总分: \(143\ Pts\)
考试过程
这次的题确实没做过... 所以人就没了
读完题 从 \(T1\) 开始 分析题目 分测试点 先写了六十分的树 四十分钟 调过大样例 四十分的基环树没写 转 \(T2\) 读完题 稍微分析了二十分钟 感觉不可做 跑路了 转 \(T3\) 分析了一下 发现有四十四分的暴力 写了个 \(O(nm)\) 的 自己跑了几组数据 一共大概半个小时 感觉四十四分没问题 回 \(T1\) 去写剩下的四十分 二十分钟想了一下 写的时候发现不对劲 又改 写了一半 感觉直接枚举环上的边断边 每次跑一个 \(O(n)\) 的会超时 去分析性质 贪了一下 写成 \(O(n)\) 的 常数略大 第一次贪假了 又调 剩四十分钟的时候调过大样例 继续看 \(T3\) 然而并没有什么进展
题解
\(T1\) 旅行
贪心贪假... 挂成 \(84\) 没想出来为什么贪心假了 改了一下 换成 \(O(n^2)\) 的就过了 虽然有点慢 但是确实能够
/*
Time: 6.6
Worker: Blank_space
Source:
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#define Abs(x) ((x) < 0 ? -(x) : (x))
#define Max(x, y) ((x) > (y) ? (x) : (y))
#define Min(x, y) ((x) < (y) ? (x) : (y))
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*--------------------------------------头文件*/
const int A = 5e3 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
/*------------------------------------常量定义*/
inline void File() {
freopen("travel.in", "r", stdin);
freopen("travel.out", "w", stdout);
}
/*----------------------------------------文件*/
int n, m, ans[A], cnt, d[A][A], s, t, vis2[A], p1, p2, pos, _ans[A];
struct edge {int v, nxt;} e[A << 1];
int head[A], ecnt;
bool vis[A], cl[A];
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
void add_edge(int u, int v) {e[++ecnt] = (edge){v, head[u]}; head[u] = ecnt;}
void dfs1(int u, int pre) {
vis[u] = 1; _ans[++cnt] = u; int tot = 0;
for(int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
if(v != pre && !vis[v] && !((u == p1 && v == p2) || (u == p2 && v == p1))) d[u][++tot] = v;
std::sort(d[u] + 1, d[u] + 1 + tot);
if(tot) for(int i = 1; i <= tot; i++)
if(!vis[d[u][i]]) dfs1(d[u][i], u);
}
void work1() {
dfs1(1, 0);
for(int i = 1; i < cnt; i++) printf("%d ", _ans[i]);
printf("%d\n", _ans[cnt]);
}
void dfs2(int u, int pre) {
vis2[u] = pre;
for(int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v; if(v == pre) continue;
if(vis2[v]) {vis2[v] = u; s = u, t = v; return ;}
else dfs2(v, u);
if(s && t) return ;
}
}
void dfs3(int u, int pre) {
for(int i = head[u], v = e[i].v; i; i = e[i].nxt, v = e[i].v)
if(cl[v] && v != pre)
{
if(v > pos) {p1 = u, p2 = v; return ;}
else dfs3(v, u);
}
}
void up_date() {
for(int i = 1; i <= cnt; i++)
if(_ans[i] > ans[i]) return ;
else if(_ans[i] < ans[i]) break;
for(int i = 1; i <= cnt; i++) ans[i] = _ans[i];
}
void work2() {
s = t = 0; dfs2(1, 0); pos = 0; memset(ans, 63, sizeof ans);
for(int i = s; vis2[i] != s; i = vis2[i])
{
p1 = i; p2 = vis2[i]; cnt = 0;
memset(vis, 0, sizeof vis); dfs1(1, 0);
up_date();
}
for(int i = 1; i < cnt; i++) printf("%d ", ans[i]); printf("%d\n", ans[cnt]);
// for(int i = s; vis2[i] != s; i = vis2[i]) cl[i] = 1; cl[t] = 1;
// if(cl[1]) t = 1;
// for(int i = head[t]; i; i = e[i].nxt) if(cl[e[i].v]) pos = Max(pos, e[i].v);
// dfs3(t, pos); work1();
}
/*----------------------------------------函数*/
int main() {
File();
n = read(); m = read(); p1 = p2 = 0;
for(int i = 1; i <= m; i++)
{
int x = read(), y = read();
add_edge(x, y); add_edge(y, x);
}
if(m == n - 1) work1();
else work2();
return 0;
}
/*
6 5
1 3
2 3
2 5
3 4
4 6
10 9
1 3
2 3
2 5
3 4
4 6
5 7
2 8
8 10
2 9
4 6
字典序最小 一定是从一号点开始
一个节点只能被经过两次 入一次 出一次 不会有左右乱窜的情况
所以在每一个点直接比较左右孩子的点的编号 贪一下
题目保证图联通 不存在自环 不存在重边
60 分的树
大样例挂了
四十分钟过 60 分的大样例
40 分的基环树
分 1 号点在不在环上进行讨论
略 先不写 去看别的题
感觉不对劲 可能有坑
环上有一次回头的机会
11 11
11 10
10 6
6 8
6 4
8 9
4 3
9 7
7 5
5 3
1 2
1 3
大样例挂了 还有一个小时
12 12
1 10
1 2
2 8
2 3
3 9
3 4
4 5
5 7
7 12
7 6
6 1
6 11
只要把环断开 和 60 的一样
考虑在哪断环 贪
从一号点进去 找一个大点的 记下来 往另一边搜 找到的第一个比记下来的那个点大的 再往下一个 断开
二十分钟 过大样例
*/
/*
贪心挂成84
改成 n 方的 过了
可能这就是这个题只能当 T1 的原因吧
*/
建议加强数据把 n 方卡掉
\(T2\) 填数游戏
真心不可做 输出样例有15分好评
看第一眼以为是状压 毕竟数据范围在那放着 推了一下 发现没法写... 弃了
正解: 推式子 打表 + 找规律
对于一道狗比题就要用狗比的做法
所以...先打个表
枚举所有情况 将经过的数字压成一个二进制数 比较两个路径的字典序 相当于比较两个二进制数的大小
记搜 存一个二元组 记录从每个点出发构成的二进制数(最小值, 最大值) 如果一个点向右走的最小值小于向下走的最大值 就不合法
直接暴力构造棋盘 按照上面的方法进行 \(check\) 每构造完一列就 \(check\) 一下 可能会稍微快一点
/*
Time: 6.6
Worker: Blank_space
Source:
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#define p1 first
#define p2 second
#define R x, y + 1, mx, my
#define D x + 1, y, mx, my
#define mk std::make_pair
#define pa std::pair <int, int>
#define Mp (mp[x][y] << mx + my - x - y)
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
/*------------------------------------常量定义*/
inline void File() {
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
}
/*----------------------------------------文件*/
int n, m, ans;
bool mp[10][10];
pa f[10][10];
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
pa check(int x, int y, int mx, int my) {
if(f[x][y].p1) return f[x][y];
if(x == mx && y == my) return f[x][y] = mk(mp[x][y], mp[x][y]);
if(x == mx) {pa tmp = check(R); return f[x][y] = mk(tmp.p1 + Mp, tmp.p2 + Mp);}
if(y == my) {pa tmp = check(D); return f[x][y] = mk(tmp.p1 + Mp, tmp.p2 + Mp);}
pa tmp1 = check(R); if(!~tmp1.p1) return f[x][y] = mk(-1, -1);
pa tmp2 = check(D); if(!~tmp2.p2 || tmp1.p1 < tmp2.p2) return f[x][y] = mk(-1, -1);
return f[x][y] = mk(tmp2.p1 + Mp, tmp1.p2 + Mp);
}
void dfs(int x, int y) {
if(y == 1 && x > 1)
{
memset(f, 0, sizeof f);
if(check(1, 1, x - 1, m).p1 == -1) return ;
if(x == n + 1) {ans++; return ;}
}
if(y == m) mp[x][y] = 0, dfs(x + 1, 1), mp[x][y] = 1, dfs(x + 1, 1);
else mp[x][y] = 0, dfs(x, y + 1), mp[x][y] = 1, dfs(x, y + 1);
}
void work() {
memset(mp, 0, sizeof mp); ans = 0; dfs(1, 1);
printf("n = %d; m = %d : %d\n", n, m, ans);
}
/*----------------------------------------函数*/
int main() {
int N = read(), M = read();
for(int i = 1; i <= N; i++)
for(int j = 1; j <= M; j++)
n = i, m = j, work();
return 0;
}
实测 \(m = 8\ n = 8\) 的数据跑了大概不太到十分钟的样子 跑完大概是这个样子的
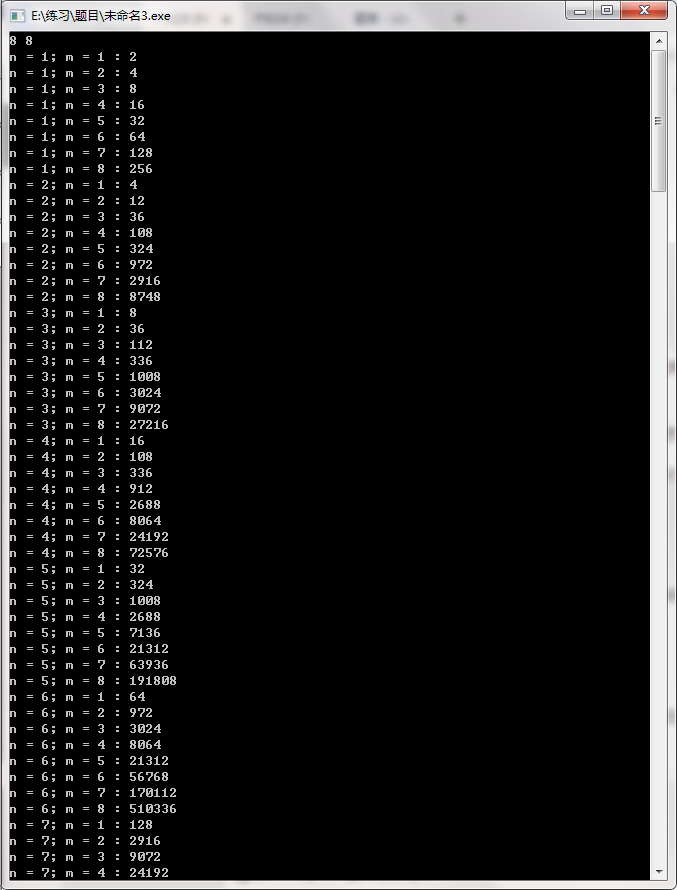
有点蒙
把数据稍微整理一下
| n, m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
| 2 | 4 | 12 | 36 | 108 | 324 | 972 | 2916 | 8748 |
| 3 | 8 | 36 | 112 | 336 | 1008 | 3024 | 9072 | 27216 |
| 4 | 16 | 108 | 336 | 912 | 2688 | 8064 | 24192 | 72576 |
| 5 | 32 | 324 | 1008 | 2688 | 7136 | 21312 | 63936 | 191808 |
| 6 | 64 | 972 | 3024 | 8064 | 21312 | 56768 | 170112 | 510336 |
| 7 | 128 | 2916 | 9072 | 24192 | 63936 | 170112 | 453504 | 1360128 |
| 8 | 256 | 8748 | 27216 | 72576 | 191808 | 510336 | 1360128 | 3626752 |
手要废了 真不错
看他一下
当 \(n\) 或 \(m\) 为 \(1\) 的时候 \(ans = 2 ^{ \max\{n, m\}}\)
别的呢
看 \(2\) 这一列
很显眼的发现
\[4 \times 3 = 12\\
12 \times 3 = 36\\
36 \times 3 = 108
\]
再看
\[108 \times 3 = 324\\
324 \times 3 = 972\\
972 \times 3 = 2916\\
2916 \times 3 = 8718
\]
似乎有规律
再看 \(3\) 这一列
\[8 \times 3 \ne 36\\
36 \times 3 \ne 112\\
112 \times 3 = 336\\
336 \times 3 = 1008\\
1008 \times 3 = 3024\\
3024 \times 3 = 9072\\
9072 \times 3 = 27216
\]
...
上面两个好像出了一点问题
再看第 \(4\) 列
\[16 \times 3 \ne 108\\
108 \times 3 \ne 336\\
336 \times 3 \ne 912\\
912 \times 3 \ne 2688\\
2688 \times 3 = 8064\\
8064 \times 3 = 24192\\
...
\]
第 \(4\) 列从第五行开始满足
第 \(5\) 列从第六行开始满足
第 \(6\) 列从第七行开始满足
可以猜测 第 \(7\) 列则应该是第八行了 那么当 \(n = 7\ m = 9\) 的时候答案应该是 \(1360128 \times 3 = 4080384\) 跑一下试试
过了许久...
大胆猜:
当 \(m > n + 1\) 的时候 \(ans_{n, m} = ans_{n, m - 1} \times 3\)
推广一下 \(ans_{n, m} = ans_{n, n + 1} \times 3^{m - n - 1}\)
好办了...
只需要再把 \(ans_{8, 9}\) 跑出来就行了 其他的就可以直接算了
代码
/*
Time: 6.6
Worker: Blank_space
Source: P5023 [NOIP2018 提高组] 填数游戏
*/
/*--------------------------------------------*/
#include<cstdio>
#define int long long
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
/*------------------------------------常量定义*/
inline void File() {
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
}
/*----------------------------------------文件*/
int n, m;
int a[10][10] = {
{0},
{0, 2, 4},
{0, 0, 12, 36},
{0, 0, 0, 112, 336},
{0, 0, 0, 0, 912, 2688},
{0, 0, 0, 0, 0, 7136, 21312},
{0, 0, 0, 0, 0, 0, 56768, 170112},
{0, 0, 0, 0, 0, 0, 0, 453504, 1360128},
{0, 0, 0, 0, 0, 0, 0, 0, 3626752, 10879488}
};
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
int power(int b, int a = 3, int res = 1) {for(; b; a = a * a % mod, b >>= 1) if(b & 1) res = res * a % mod; return res;}
/*----------------------------------------函数*/
signed main() {
n = read(); m = read(); if(n > m) Swap(n, m);
if(n == 1) printf("%lld", 1 << m);
else if(n == m || m == n + 1) printf("%lld", a[n][m]);
else printf("%lld", a[n][n + 1] * power(m - n - 1) % mod);
return 0;
}
\(T3\) 保卫王国
\(44\ Pts\) 的暴力分送的
考虑正解
首先是 \(dp\)
状态 \(f_{u, 0/1}\) 表示以 \(u\) 为根的子树 \(u\) 点选不选时的最小花费
转移
\[f_{u, 0} = \sum f_{v, 1}\\
f_{u, 1} = \sum \min \{f_{v, 0}, f_{v, 1} \}
\]
先把没有限制的情况下的 \(dp\) 数组跑出来
对于每一个询问 只修改两个点 设为 \(u\) 和 \(v\) 主要造成影响的只有 \(u\) 和 \(v\) 两点到这两点的 \(LCA\) 设为 \(L\) 以及 \(L\) 到根节点之间的路径 其他的子树可以用之前跑出来的答案直接代入处理 那这几条链怎么办
对于 \(u\) 与 \(v\) 的操作无非就是否定一些 \(dp\) 状态 也就是将这些 \(dp\) 值设为 \(INF\) 考虑预处理一个数组加速转移 由于已经跑过一边 \(dp\) 所以这个数组中就不再需要记录 \(dp\) 值了 只需要记录点的选取与否即可
设 \(g_{x, y, 0/0, 0/1}\) 表示 \(x\) 点选与不选 \(y\) 点选与不选时 \(x\) 到 \(y\) 的链的最优 \(dp\) 值
但是我们想要的是优化 加速转移 所以就有了倍增
设 \(g_{u, j, 0/1, 0/1}\) 表示 \(u\) 点选与不选 \(u\) 点的 \(2^j\) 级祖先选与不选时 从 \(u\) 到 \(u\) 的 \(2^j\) 祖先之间的链上的最优 \(dp\) 值
转移时 考虑 \(u\) 到 \(2^{j - 1}\) 级祖先与 \(u\) 的 \(2^{j - 1} + 1\) 级祖先到 \(2^j\) 级祖先取 \(\min\) 即可
然后还有个问题 这条链上的其他子树怎么办
这些子树的 \(dp\) 值已经有了 那么直接拿来用 将其他子树的 \(dp\) 值强行计入上面的 \(g\) 数组中 相当于在整个祖先子树中减去 \(u\) 子树的影响
再考虑其他问题 一开始跑出来的 \(dp\) 值都是包含一个点和这个点的子树的 当在链上更新 \(u\) 的父节点 \(fa\) 的 \(dp\) 值的时候 \(f_{fa, 0/1}\) 中必然包含了 \(u\) 点的贡献 需要将这一贡献消去 设 \(u\) 点新的 \(dp\) 值为 \(K\) 类似于换根
\[f_{fa, 0} = f_{fa, 0} - f_{u, 1} + K\\
f_{fa, 1} = f_{fa, 1} - \min\{f_{u, 0}, f_{u, 1} \} + K
\]
然后 \(LCA\) 怎么搞
将 \(u\) 和 \(v\) 都跳到 \(LCA\) 的儿子处 单独处理
再然后
就没有然后了
算法流程就是
预处理 \(f\) 和 \(g\) 询问的时候跳点到 \(LCA\) 再从 \(LCA\) 继续往上跳 沿途更新状态 最后处理根节点
设倍增数组为 \(fa_{u, j}\) 设 \(fa\) 表示 \(fa_{u, j - 1}\)
\(g\) 数组的转移
\[g_{u, i, 0, 0} = \min\{g_{u, i - 1, 0, 0} + g_{fa, i - 1, 0, 0}, g_{u, i - 1, 0, 1} + g_{fa, i - 1, 1, 0} \}\\
g_{u, i, 0, 1} = \min\{g_{u, i - 1, 0, 0} + g_{fa, i - 1, 0, 1}, g_{u, i - 1, 0, 1} + g_{fa, i - 1, 1, 1} \}\\
g_{u, i, 1, 0} = \min\{g_{u, i - 1, 1, 0} + g_{fa, i - 1, 0, 0}, g_{u, i - 1, 1, 1} + g_{fa, i - 1, 1, 0} \}\\
g_{u, i, 1, 1} = \min\{g_{u, i - 1, 1, 0} + g_{fa, i - 1, 0, 1}, g_{u, i - 1, 1, 1} + g_{fa, i - 1, 1, 1} \}
\]
代码
极大值注意开大一下 因为开小了 调了半小时才看出来
/*
Time: 6.6
Worker: Blank_space
Source: P5024 [NOIP2018 提高组] 保卫王国
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#define int long long
#define Min(x, y) ((x) < (y) ? (x) : (y))
#define Swap(x, y) ((x) ^= (y) ^= (x) ^= (y))
/*--------------------------------------头文件*/
const int B = 1e5 + 7;
const int mod = 1e9 + 7;
const int INF = 1e18;
/*------------------------------------常量定义*/
inline void File() {
freopen("defense.in", "r", stdin);
freopen("defense.out", "w", stdout);
}
/*----------------------------------------文件*/
int n, m, p[B], dep[B], f[B][2], fa[B][20], g[B][20][2][2], lg[B];
struct edge {int v, nxt;} e[B << 1];
int head[B], ecnt;
char type[10];
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
void add_edge(int u, int v) {e[++ecnt] = (edge){v, head[u]}; head[u] = ecnt;}
void dfs1(int u, int pre) {
dep[u] = dep[pre] + 1; f[u][1] = p[u]; fa[u][0] = pre;
for(int i = 1; i <= lg[dep[u]]; i++) fa[u][i] = fa[fa[u][i - 1]][i - 1];
for(int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v; if(v == pre) continue;
dfs1(v, u); f[u][0] += f[v][1]; f[u][1] += Min(f[v][0], f[v][1]);
}
}
void dfs2(int u, int pre) {
g[u][0][0][0] = INF; g[u][0][1][0] = f[pre][0] - f[u][1];
g[u][0][0][1] = g[u][0][1][1] = f[pre][1] - Min(f[u][0], f[u][1]);
for(int i = 1, F = fa[u][i - 1]; i <= 18; i++, F = fa[u][i - 1])
g[u][i][0][0] = Min(g[u][i - 1][0][0] + g[F][i - 1][0][0], g[u][i - 1][0][1] + g[F][i - 1][1][0]),
g[u][i][0][1] = Min(g[u][i - 1][0][0] + g[F][i - 1][0][1], g[u][i - 1][0][1] + g[F][i - 1][1][1]),
g[u][i][1][0] = Min(g[u][i - 1][1][0] + g[F][i - 1][0][0], g[u][i - 1][1][1] + g[F][i - 1][1][0]),
g[u][i][1][1] = Min(g[u][i - 1][1][0] + g[F][i - 1][0][1], g[u][i - 1][1][1] + g[F][i - 1][1][1]);
for(int i = head[u]; i; i = e[i].nxt) if(e[i].v != pre) dfs2(e[i].v, u);
}
void work(int u, int x, int v, int y) {
if(dep[u] < dep[v]) Swap(u, v), Swap(x, y);
int u0 = INF, u1 = INF, v0 = INF, v1 = INF, l0 = INF, l1 = INF, lca, ans;
x ? u1 = f[u][1] : u0 = f[u][0]; y ? v1 = f[v][1] : v0 = f[v][0];
for(int i = lg[dep[u] - dep[v]], t0, t1; ~i; i--) if(dep[fa[u][i]] >= dep[v])
t0 = u0, t1 = u1, u0 = Min(t0 + g[u][i][0][0], t1 + g[u][i][1][0]), u1 = Min(t0 + g[u][i][0][1], t1 + g[u][i][1][1]), u = fa[u][i];
if(u == v) lca = u, y ? l1 = u1 : l0 = u0;
else
{
for(int i = lg[dep[u] - 1], t0, t1, s0, s1; ~i; i--) if(fa[u][i] != fa[v][i])
t0 = u0, t1 = u1, s0 = v0, s1 = v1,
u0 = Min(t0 + g[u][i][0][0], t1 + g[u][i][1][0]), u1 = Min(t0 + g[u][i][0][1], t1 + g[u][i][1][1]), u = fa[u][i],
v0 = Min(s0 + g[v][i][0][0], s1 + g[v][i][1][0]), v1 = Min(s0 + g[v][i][0][1], s1 + g[v][i][1][1]), v = fa[v][i];
lca = fa[u][0]; l0 = f[lca][0] - f[u][1] - f[v][1] + u1 + v1;
l1 = f[lca][1] - Min(f[u][0], f[u][1]) - Min(f[v][0], f[v][1]) + Min(u0, u1) + Min(v0, v1);
}
if(lca == 1) ans = Min(l0, l1);
else
{
for(int i = lg[dep[lca] - 2], t0, t1; ~i; i--) if(dep[fa[lca][i]] > 1)
t0 = l0, t1 = l1, l0 = Min(t0 + g[lca][i][0][0], t1 + g[lca][i][1][0]), l1 = Min(t0 + g[lca][i][0][1], t1 + g[lca][i][1][1]), lca = fa[lca][i];
ans = Min(f[1][0] - f[lca][1] + l1, f[1][1] - Min(f[lca][0], f[lca][1]) + Min(l0, l1));
}
if(ans >= INF) puts("-1");
else printf("%lld\n", ans);
}
/*----------------------------------------函数*/
signed main() {
File();
n = read(); m = read(); scanf("%s", type);
for(int i = 1; i <= n; i++) p[i] = read();
for(int i = 2; i <= n; i++) {int x = read(), y = read(); add_edge(x, y); add_edge(y, x); lg[i] = lg[i >> 1] + 1;}
dfs1(1, 0); dfs2(1, 0);
for(int i = 1; i <= m; i++)
{
int a = read(), x = read(), b = read(), y = read();
work(a, x, b, y);
}
return 0;
}
