Codeforces Round #678 (Div. 2)
Codeforces Round #678 (Div. 2)
题意:有一个有 n 个数的序列 a ,以及一个数 m ,问能否给序列a重新排序,能够满足式子 $\sum_{i=1}^{n}\sum_{j=i}^{n}\frac{a_{j}}{j}=m$。
思路:稍微计算一下便可以发现$1\times \frac{a_{1}}{1}+2\times \frac{a_{2}}{2}+...+n\times \frac{a_{n}}{n}=a_{1}+a_{2}+...+a_{n}$,其实这道题就是问序列的所有数之和是否为m。
代码:

#include<bits/stdc++.h> using namespace std; int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int t; cin>>t; while(t--){ int n,m,ans=0,get_num; cin>>n>>m; while(n--){ cin>>get_num; ans+=get_num; } if(ans==m) cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0; }
题意:t 组数据,每组数据给一个 n ,构造一个以 n 为边长的数字方阵,要求每个数都不能是质数,但是每行每列之和都为质数。
思路:构造,对于每一个 n ,可以考虑从 n 开始往上找质数,每找到一个质数 p 尝试构造一次,构造方法为主对角线元素为$p-n+1$,其余位置上的元素均为1,这样如果$p-n+1$不是质数,那就可以保证满足题意。(因为每个$p-n+1$都在主对角线上,所以每个$p-n+1$只对当前行列造成影响,所以这样构造可以保证每一行每一列的和都为我们找到的质数 p )。
代码:

#include<bits/stdc++.h> using namespace std; bool is_prime(int n){ if(n==1) return false; for(int i=2;i*i<=n;i++){ if(n%i==0) return false; } return true; } int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int t,n; cin>>t; while(t--){ cin>>n; int p=n; while(!(is_prime(p) && !is_prime(p-n+1))) p++; for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if(i==j) cout<<p-n+1<<" "; else cout<<1<<" "; } cout<<endl; } cout<<endl; } return 0; }
题意:有一个序列有 n 个数,如果序列有序,则按照如下代码可以找到 pos 位置上的数字 x ,现在询问如果序列无序,而且仍然可以用下面这段代码找到位于pos 位置上的数字 x ,请问这样的序列有多少种,答案对1e9+7取模。

思路:按照代码我们可以得知,算至pos的路径是固定的,而且对于每次循环 left 和 right 所产生的 middle ,我们都可以用来确定 a[middle] 和 x 的大小关系,那么我们就可以确定某些位置的数字是严格大于 x 的,某些位置的数字是严格小于 x 的,这样我们就可以用全排列和乘法原理算出答案。
我们可以来进行二分,当 middle > pos 时,a[middle]是大于 x 的 , 大于 x 的计数变量加一;当middle < pos 时,a[middle]是小于 x 的,小于x的计数变量加一;二分完成后,会剩下$n-big-small$个位置上的数无法确定。所以答案就是从$n-x$个大于 x 的数选 big 个数的全排列乘以从$x-1$个小于 x 的数选 small 个数的全排列乘以剩下$n-big-small-1$个数的全排列,即$A_{n-x}^{big}\times A_{x-1}^{small}\times A_{n-big-small-1}^{n-big-small-1}$。当然,如果big>n-x或者small>x-1的话,不存在这样的排列,答案为0。
代码:

#include<bits/stdc++.h> using namespace std; typedef long long ll; ll mod=1e9+7; int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); long long n,x,pos,l,r,big=0,small=0,ans=1; cin>>n>>x>>pos; l=0;r=n; while(l<r){ long long mid=(l+r)/2; if(mid==pos){ l=mid+1; }else if(mid>pos){ r=mid; big++; }else if(mid<pos){ l=mid+1; small++; } } if(small>=x || big>n-x){ cout<<0<<endl; }else{ for(ll i=x-1,j=1;j<=small;i--,j++){ ans=(ans*i)%mod; } for(ll i=n-x,j=1;j<=big;i--,j++){ ans=(ans*i)%mod; } for(ll i=1;i<=n-small-big-1;i++){ ans=(ans*i)%mod; } cout<<ans<<endl; } return 0; }
题意:城市有 n 个区域编号为1...n,n-1 个单向通路,而且1号区域为主区域,保证主区域可以到达任何其它区域。现在给出 i 号区域有 ai 个人,且一伙土匪位于主区域,他们希望抓住更多的人,他们会一只往前走,直至最后的区域没有通往其它区域的路,市民则可以选择通路进行逃跑,当没有通往其它区域的路且土匪位于该区域时市民会被抓住。现在土匪想要抓住尽可能多的人,而市民则希望尽可能少的人被抓住,两方都采取最优解。问土匪最多能抓到多少人。
思路:对于某一个区域,我们考虑当前区域时,土匪最多能抓多少人 ,那么这个问题依赖于该区域可以通往的其它区域所计算的结果。所以这个问题我们可以拆成一个一个的子问题然后用递归的思想来解决。对于任意一个区域 x ,我们需要算出这个当前区域以及这个区域能达到的区域的总人数num,当前区域之后的分支线路数lu,以及人数最多的那条路的人数maxx(这个maxx是考虑到位于尾节点的人无法逃跑),将这三个值放入一个结构体中递归时返回。
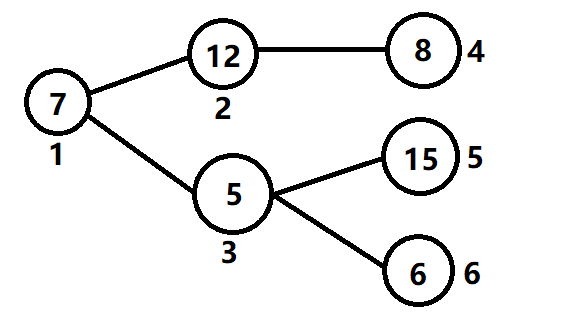
举个例子,对于上图这个例子考虑节点1就需要节点2和节点3的值,2需要4的值,3需要5和6的值。对于4节点{num=8,lu=1,maxx=8},对于5节点{num=15,lu=1,maxx=15},对于6节点{num=6,lu=1,maxx=6},对于3节点,这时我们计算的{num=当前节点的人数+所有子问题返回的人数 num 之和,lu=所有子问题返回的路数 lu 之和,maxx=max( maxx,刚算出的总人数num/刚算出的路数lu+(1) ) } (括号内的1分情况讨论,若num整除lu则不加,不整除则加),所以3节点{num=15+6+5=26,lu=1+1=2,maxx=max(15,26/2=13)=15}。对于2节点{num=12+8=20,lu=0+1,maxx=(0,20/1)=20},对于节点1{num=20+26+7=52,lu=1+2=3,maxx=max(20,15,52/3+1)=20}所以最后答案为20。
代码:

#include<bits/stdc++.h> using namespace std; typedef long long ll; vector<vector<int> >ro(200005); ll num[200005]; struct node{ ll lu,sum,maxx; }now,get_solve; node solve(int root){ //cout<<"cont "<<root<<endl; if(ro[root].size()==0){ now.lu=1;now.sum=num[root];now.maxx=num[root]; return now; } ll lu=0,sum=num[root],maxx=0,mark=0; for(int i=0;i<ro[root].size();i++){ get_solve=solve(ro[root][i]); lu+=get_solve.lu; sum+=get_solve.sum; maxx=max(get_solve.maxx,maxx); } now.lu=lu;now.sum=sum; if(sum%lu!=0) mark++; now.maxx=max(maxx,sum/lu+mark); return now; } int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int n,get_num,mark=0; cin>>n; for(int i=2;i<=n;i++){ cin>>get_num; ro[get_num].push_back(i); } for(int i=1;i<=n;i++){ cin>>num[i]; } node ans=solve(1); if(ans.sum%ans.lu!=0) mark++; cout<<max(ans.maxx,ans.sum/ans.lu+mark)<<endl; return 0; }
题意:我们称一个序列的MEX为没有在这个序列中出现的最小正整数,如MEX[1,4,6,5,3]=2。如果从 a 序列左端删去 x 个连续数字,右端删去 y 个连续数字,可以得到序列 b ,那么称序列 b 就是序列 a 的子序列( a 和 b 相等也可以称 b 为 a 的子序列)。求所有子序列的MEX的MEX。
思路:可以从左往右遍历序列,对于每个数字 ai 考虑 ai 是否能作为一个序列的MEX,利用线段树维护某一段数字出现的位置的最小值。那么如果数字 1 到数字$a_{i}-1$都出现过且这些数字上一次出现的位置的最小值大于 ai 上一次出现的位置,那么 ai 就可以作为一段序列的MEX。遍历之后,会发现我们刚才的操作并没有做完全,序列右边还有一些情况没有处理到,那么现在开始从 1 到 n+1 进行遍历,记为数字 i ,查看 i 是否能作为剩下情况中的 MEX ,如果不能则 i极为最终答案,若 1 到 n+1 都可以作为子序列的 MEX,则最终答案为 n+2 。(注意数字 1 的处理)。
代码:

#include<bits/stdc++.h> using namespace std; const int maxn=100005; bool flag[maxn]; int appear[maxn]; class Seg_Tree { public: int n,max_num=1e9+7; int num[maxn],tree[maxn<<2]; void build(int l,int r,int node){ tree[node]=0; if(l==r) return; int mid=(l+r)>>1; build(l,mid,node<<1); build(mid+1,r,node<<1|1); } void update(int l,int r,int pos,int val,int node){ if(l==r){ tree[node]=val; return; } int mid=(l+r)>>1; if(pos<=mid) update(l,mid,pos,val,node<<1); else update(mid+1,r,pos,val,node<<1|1); tree[node]=min(tree[node<<1],tree[node<<1|1]); } int query(int l,int r,int node,int ql,int qr){ if(ql>qr) return 0; if(l>qr || r<ql) return max_num; if(l>=ql && r<=qr) return tree[node]; int mid=(l+r)>>1,x,y; x=query(l,mid,node<<1,ql,qr); y=query(mid+1,r,node<<1|1,ql,qr); return min(x,y); } }; int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); Seg_Tree seg_tree; memset(flag,false,sizeof(flag)); cin>>seg_tree.n; int ans=seg_tree.n+2; for(int i=1;i<=seg_tree.n;i++){ cin>>seg_tree.num[i]; if(seg_tree.num[i]>1) flag[1]=true; } seg_tree.build(1,seg_tree.n,1); for(int i=1;i<=seg_tree.n;i++){ if(seg_tree.query(1,seg_tree.n,1,1,seg_tree.num[i]-1)>appear[seg_tree.num[i]]) flag[seg_tree.num[i]]=true; seg_tree.update(1,seg_tree.n,seg_tree.num[i],i,1); appear[seg_tree.num[i]]=i; } for(int i=1;i<=seg_tree.n+1;i++){ if(flag[i]) continue; if(seg_tree.query(1,seg_tree.n,1,1,i-1)>appear[i]) continue; else{ ans=i; break; } } cout<<ans<<endl; return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号