Codeforces Round #604 (Div. 2)
Codeforces Round #604 (Div. 2)
题意:有一个字符串由a、b、c三种字符组成,现在字符串并不完整,残缺部分用?代替,问能否将字符串残缺部分补充完整且整个字符串任意相邻的字符都不同。
思路:顺序将残缺补齐即可,对于任意的“m??n”都可以转化为"mp?n",且无论p与n是否相同,均有字符可以填入。所以只要题中明确给出的字符不存在相邻且相同的情况,就一定可以完成。

#include<bits/stdc++.h> using namespace std; int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int total; string s; cin>>total; while(total--){ cin>>s; if(s.size()==1){ if(s[0]=='?'){ cout<<'a'<<endl; }else{ cout<<s<<endl; } }else{ for(int i=0;i<s.size();i++){ if(s[i]=='?'){ if(i==0){ if(s[i+1]=='a'){ s[i]='b'; }else{ s[i]='a'; } }else if(i==s.size()-1){ if(s[i-1]=='a'){ s[i]='b'; }else{ s[i]='a'; } }else{ if(s[i-1]=='a'){ if(s[i+1]=='b') s[i]='c'; else if(s[i+1]=='c') s[i]='b'; else s[i]='b'; }else if(s[i+1]=='a'){ if(s[i-1]=='b') s[i]='c'; else if(s[i-1]=='c') s[i]='b'; else s[i]='b'; }else{ s[i]='a'; } } } } bool flag=true; for(int i=0;i<s.size()-1;i++){ if(s[i]==s[i+1]){ flag=false; break; } } if(flag){ cout<<s<<endl; }else{ cout<<-1<<endl; } } } return 0; }
题意:给你一组数字 [p1,p2,p3,...,pn],请你找出所有的美丽数字。定义存在左右边界为l,r,且对于数组 [pl,pl+1,pl+2,...,pr]是1,2,3,....m的一种排列,那么m就是一个美丽的数字。最后输出一个长为n的字符串,若i为美丽数那么第i位位1,若i部位美丽数那么第i位为0
思路:拿到题就直接想暴力搞了,维护一棵线段树求区间和,先读入每一个数,记下每个数在数组之中的位置,然后从数字1到n开始遍历(记为 i ),每次遍历将该数字 i 所在的位置加1,然后对区间 [ l , r ]求和(l为遍历过程中出现过的最小的下标,r为遍历过程中出现的最大下标),若区间和等于区间长度,则该数字 i 为美丽数字。最后输出形成的01串。
线段树为写过的模板,多余的东西懒得删除了。

#include<bits/stdc++.h> #define ll int using namespace std; const ll MAXN = 2e5 + 10; struct Tree { ll l,r; ll sum; ll lazy; ll maxn; ll minn; } tree[MAXN<<2]; void push_up(ll node) { tree[node].sum=tree[node<<1].sum+tree[node<<1|1].sum; tree[node].maxn=max(tree[node<<1].maxn,tree[node<<1|1].maxn); tree[node].minn=min(tree[node<<1].minn,tree[node<<1|1].minn); } void push_down(ll node, ll length) { if(tree[node].lazy) { tree[node<<1].lazy+=tree[node].lazy; tree[node<<1|1].lazy+=tree[node].lazy; tree[node<<1].sum+=(length-(length>>1))*tree[node].lazy; tree[node<<1|1].sum+=(length>>1)*tree[node].lazy; tree[node<<1].minn+=tree[node].lazy; tree[node<<1|1].minn+=tree[node].lazy; tree[node<<1].maxn+=tree[node].lazy; tree[node<<1|1].maxn+=tree[node].lazy; tree[node].lazy = 0; } } void build(ll l,ll r, ll node) { tree[node].lazy = 0; tree[node].l=l; tree[node].r=r; if(l==r) { tree[node].sum=0; tree[node].minn=tree[node].sum; tree[node].maxn=tree[node].sum; return; } ll mid=(l+r)>>1; build(l,mid,node<<1); build(mid+1,r,node<<1|1); push_up(node); } void update(ll left,ll right,ll key, ll node) { if(tree[node].l>=left && tree[node].r<=right) { tree[node].sum+=(tree[node].r-tree[node].l+1)*key; tree[node].minn+=key; tree[node].maxn+=key; tree[node].lazy+=key; return; } push_down(node,tree[node].r-tree[node].l+1); ll mid=(tree[node].r+tree[node].l)>>1; if(left<=mid) update(left,right,key,node<<1); if(right>mid) update(left,right,key,node<<1|1); push_up(node); } ll query(ll left,ll right,ll node) { if(tree[node].l>=left && tree[node].r<=right) { return tree[node].sum; } push_down(node,tree[node].r-tree[node].l+1); ll mid=(tree[node].r+tree[node].l)>>1; ll ans=0; if(left<=mid) ans+=query(left,right,node<<1); if(right>mid) ans+=query(left,right,node<<1|1); return ans; } ll query_min(ll left,ll right,ll node) { if(tree[node].l>=left && tree[node].r<=right) { return tree[node].minn; } push_down(node,tree[node].r-tree[node].l+1); ll mid=(tree[node].r+tree[node].l)>>1; ll ans=0x7fffffff; if(left<=mid) ans=min(ans,query_min(left,right,node<<1)); if(right>mid) ans=min(ans,query_min(left,right,node<<1|1)) ; return ans; } ll query_max(ll left,ll right,ll node) { if(tree[node].l>=left && tree[node].r<=right) { return tree[node].maxn; } push_down(node,tree[node].r-tree[node].l+1); ll mid=(tree[node].r+tree[node].l)>>1; ll ans=-0x7fffffff; if(left<=mid) ans=max(ans,query_max(left,right,node<<1)); if(right>mid) ans=max(ans,query_max(left,right,node<<1|1)); return ans; } int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int total; cin>>total; while(total--){ int n,get_num; string s; cin>>n; build(1,n,1); vector<int>vec(n+1); for(int i=1;i<=4*n;i++){ tree[i].sum=0; } for(int i=1;i<=n;i++){ cin>>get_num; vec[get_num]=i; } int l=0x7fffffff,r=0; for(int i=1;i<=n;i++){ l=min(vec[i],l); r=max(vec[i],r); update(vec[i],vec[i],1,1); int ss=query(l,r,1); if(r-l+1==ss){ s.push_back('1'); }else{ s.push_back('0'); } } cout<<s<<endl; } return 0; }
题意:有n个人打比赛,每个人做了pi道题,现在要给这些人发奖牌,规定金、银、铜三种奖牌每种至少有1个,金牌的个数严格小于银牌且金牌的个数严格小于铜牌,获得金牌的人做题一定比得银牌的人做题数目多,获得银牌的人一定做题数目比铜牌多,获得铜牌的人做的题一定比没获得奖牌的人做的题多。金银铜牌的总数不得多于人数的一半。问最多能颁发多少个奖牌,输出金银铜个数(任意符合条件的结果即可)。
思路:先统计一共有多少种不同的做题情况(做出n个题有多少人,做出m个题有多少人...),金牌的数越少,其他奖牌才可能尽可能的多,所以金牌越少越好,最高的做题数对应的人数为金牌的人数。然后找银牌个数,只要银牌个数比金牌多即可,剩下的都留给铜牌,最后尽可能多的给铜牌,只要奖牌数不大于人数一半即可。判断是否符合条件,若符合则输出,否则发不出奖牌。

#include<bits/stdc++.h> using namespace std; bool judge(int x,int n){ if(x>n/2){ return false; } } int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int total,n; cin>>total; while(total--){ cin>>n; vector<long long>vec; vec.push_back(0); long long num=0,sum=0,pre_num=0; for(int i=1;i<=n;i++){ cin>>num; if(i>=2){ if(num!=pre_num){ vec.push_back(sum); } } sum++; pre_num=num; } vec.push_back(sum); int g=vec[1],b=0,s=0,j; bool flag=false; for(int i=2;i<vec.size();i++){ if(vec[i]-g>g){ flag=true; b=vec[i]-g; j=i; break; } } if(flag){ for(int i=j;i<vec.size();i++){ if(vec[i]-g-b>g && vec[i]<=n/2){ s=vec[i]-g-b; } } if(s==0){ cout<<"0 0 0"<<endl; }else{ cout<<g<<" "<<b<<" "<<s<<endl; } }else{ cout<<"0 0 0"<<endl; } } return 0; }
题意:定义一个队列如果任意相邻的元素的绝对值等于1,则这个队列为美丽队列,现在又a个0,b个1,c个2,d个3,问能否组成美丽队列,若可以按顺序输出该队列。
思路:分类讨论,我写的太复杂了= =

#include<bits/stdc++.h> using namespace std; int main(){ ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); vector<int>ans; bool flag=true; int num[4]; for(int i=0;i<4;i++){ cin>>num[i]; } int sum1=num[0]+num[2]; int sum2=num[1]+num[3]; if(num[0]>num[1] || num[3]>num[2]){ if(num[0]==0 && num[1]==0){ if(abs(num[2]-num[3])<=1){ cout<<"YES"<<endl; if(num[2]>num[3]){ for(int i=0;i<num[3];i++){ ans.push_back(2); ans.push_back(3); } ans.push_back(2); }else if(num[3]>num[2]){ for(int i=0;i<num[2];i++){ ans.push_back(3); ans.push_back(2); } ans.push_back(3); }else{ for(int i=0;i<num[3];i++){ ans.push_back(2); ans.push_back(3); } } for(int i=0;i<ans.size();i++){ cout<<ans[i]<<" "; }cout<<endl; }else{ cout<<"NO"<<endl; } }else if(num[2]==0 && num[3]==0){ if(abs(num[0]-num[1])<=1){ cout<<"YES"<<endl; if(num[0]>num[1]){ for(int i=0;i<num[1];i++){ ans.push_back(0); ans.push_back(1); } ans.push_back(0); }else if(num[1]>num[0]){ for(int i=0;i<num[0];i++){ ans.push_back(1); ans.push_back(0); } ans.push_back(1); }else{ for(int i=0;i<num[0];i++){ ans.push_back(0); ans.push_back(1); } } for(int i=0;i<ans.size();i++){ cout<<ans[i]<<" "; }cout<<endl; }else{ cout<<"NO"<<endl; } }else{ cout<<"NO"<<endl; } }else if(sum1==sum2){ for(int i=0;i<num[0];i++){ ans.push_back(0); ans.push_back(1); } num[1]-=num[0];num[0]=0; for(int i=0;i<num[1];i++){ ans.push_back(2); ans.push_back(1); } for(int i=0;i<num[3];i++){ ans.push_back(2); ans.push_back(3); } cout<<"YES"<<endl; for(int i=0;i<ans.size();i++){ cout<<ans[i]<<" "; }cout<<endl; }else if(sum1-1==sum2){ for(int i=0;i<num[0];i++){ ans.push_back(0); ans.push_back(1); } num[1]-=num[0];num[0]=0; for(int i=0;i<num[1];i++){ ans.push_back(2); ans.push_back(1); } for(int i=0;i<num[3];i++){ ans.push_back(2); ans.push_back(3); } ans.push_back(2); cout<<"YES"<<endl; for(int i=0;i<ans.size();i++){ cout<<ans[i]<<" "; }cout<<endl; }else if(sum1+1==sum2){ for(int i=0;i<num[0];i++){ ans.push_back(1); ans.push_back(0); } ans.push_back(1); num[1]-=num[0]+1;num[0]=0; for(int i=0;i<num[1];i++){ ans.push_back(2); ans.push_back(1); } for(int i=0;i<num[3];i++){ ans.push_back(2); ans.push_back(3); } cout<<"YES"<<endl; for(int i=0;i<ans.size();i++){ cout<<ans[i]<<" "; }cout<<endl; }else{ cout<<"NO"<<endl; } return 0; }
题意:现在要通过n面镜子,每天会有pi的概率通过该镜子,通过了该镜子则转天前往下一面镜子,没通过则返回到第一面镜子,问通过所有镜子的天数的期望值。
思路:通过所有镜子相当于达到第n+1个镜子,我们设计假定最终目标点n+1,ei为从点i出发到n+1这个点的期望天数,那么我们的答案就是e1,而初始状态en+1=0。我们可以得出ei=ei+1·pi+(1-pi)·e1+1。通过这个式子我们得出:
e1=e2·p1+(1-p1)·e1+1 、e2=e3·p2+(1-p2)·e1+1、e3=e4·p3+(1-p3)·e1+1、……通过代换我们可以得到![]() 和
和![]() 最终我们可以得到如下结果:
最终我们可以得到如下结果:
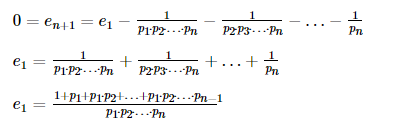

#include<bits/stdc++.h> using namespace std; const long long MOD2=998244353; long long qpow(long long a,long long b,const long long &mod){ a=a%mod; long long ans=1; while(b){ if(b&1){ ans=ans*a%mod; } a=a*a%mod; b>>=1; } return ans; } long long inv(long long a,const long long &mod){ return qpow(a,mod-2,mod); } int main() { ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int total; long long ans=0,num,cont=0; cin>>total; while(total--){ cin>>num; cont=ans+1;cont%=MOD2; cont*=100; cont%=MOD2; cont=cont*inv(num,MOD2);cont%=MOD2; ans=cont; } cout<<ans<<endl; return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号