刷刷刷 Day 14| 二叉树的遍历

144. 二叉树的前序遍历

LeetCode题目要求

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。
示例

输入：root = [1,null,2,3]
输出：[1,2,3]

解题思路

最重要的要明白什么是二叉树的前序遍历：即从中间节点开始到左节点再到右节点的遍历过程，可简称为【中左右】遍历
如下图标识的遍历过程，在过程中下面指向的 null ，就是说明到子节点了，如果这是我们知道左节点到了子节点，那就要从右节点开始。

上代码，递归实现

class Solution {
 
    public List<Integer> preorderTraversal(TreeNode root) {
        // 前序遍历即：从中间节点开始到左节点再到右节点的遍历过程，可简称为【中左右】遍历
        
        // 用 List 来存储遍历的结果
        List<Integer> res = new ArrayList<>();
        preorder(root, res);
 
        return res;
    }
 
    public void preorder(TreeNode curr, List<Integer> res) {
        // 1、先拿中节点，
        // 2、判断左节点，如果左不为空，那么又作为新的中节点，重复 1、2，直到节点为空
        // 3、判断右节点，如果右不为空，那么又作为新的中节点，重复 1、3，直到节点为空
 
        if (curr == null) {
            return;
        }
 
        res.add(curr.val);
        preorder(curr.left, res);
        preorder(curr.right, res);
    }
}

上代码，迭代实现

class Solution {
 
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
 
        if (root == null) {
            return res;
        }
 
        // 通过栈来实现，将二叉树的以 中右左的顺序 压入栈中，出栈时的顺序才是中左右 
        Deque<TreeNode> stack = new ArrayDeque<>();
        stack.push(root);
 
        // 开始遍历栈，如果栈不为空，就先出栈
        while (!stack.isEmpty()) {
            TreeNode curr = stack.pop();
            res.add(curr.val);
 
            if (curr.right != null) stack.push(curr.right);
            if (curr.left != null) stack.push(curr.left);
        }
        return res;
    }
}

145. 二叉树的后序遍历

LeetCode题目要求

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。
示例

输入：root = [1,null,2,3]
输出：[3,2,1]

解题思路

最重要的要明白什么是二叉树的后序遍历：即从左节点开始到右节点再到中间节点的遍历过程，可简称为【左右中】遍历
如下图标识的遍历过程，总是从最左节点开始的。

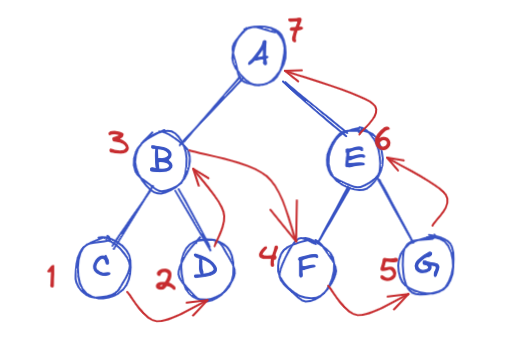
上代码，递归实现

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        // 存储结果
        List<Integer> res = new ArrayList<>();
        postorder(root, res);
        return res;
    }
 
    public void postorder(TreeNode node, List<Integer> res) {
        if (node == null) {
            return;
        }
 
        // 从左节点开始递归，这里从root 开始一直到最左子节点，才能继续找右节点，但是右节点为空，那么就把当前左节点的值放入结果
        postorder(node.left, res);
        // 从右节点开始递归
        postorder(node.right, res);
        // 将当前节点值放入结果集
        res.add(node.val);
    }
}

上代码，迭代实现

class Solution {
 
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
 
        if (root == null) {
            return res;
        }
 
        Deque<TreeNode> stack = new ArrayDeque<>();
         
        // 后序遍历： 左右中,  前序遍历的顺序是 中左右，
        // 那么可以在入栈时调整顺序变成 中左右，出栈顺序为 中右左, 然后再反转结果就是我们需要的
        stack.push(root);
 
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            res.add(node.val);
            if (node.left != null) stack.push(node.left);
            if (node.right != null) stack.push(node.right);
        }
 
        Collections.reverse(res);
        return res;
    }
}

94. 二叉树的中序遍历

LeetCode题目要求

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。
示例

输入：root = [1,null,2,3]
输出：[1,3,2]

解题思路

最重要的要明白什么是二叉树的中序遍历：即从左节点开始到中间节点再到右节点的遍历过程，可简称为【左中右】遍历
如下图标识的遍历过程，总是从最左节点开始的。

上代码，递归实现

class Solution {
 
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }
 
    public void inorder(TreeNode node, List<Integer> res) {
        if (node == null) {
            return;
        }
        // 左中右
        inorder(node.left, res);
        res.add(node.val);
        inorder(node.right, res);
    }
}

上代码，迭代实现

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
 
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode node = root;
        while (node != null || !stack.isEmpty()) {
            // 中序遍历的为 左中右，使用栈时，入栈时，从根一直遍历左节点，都入栈
            if (node != null) {
                stack.push(node);
                node = node.left;
            } else {
                // 当上面的操作左节点都入栈后，此时栈不为空，开始出栈操作，就是左节点出栈并将其值入结果集，同时取右节点
                node = stack.pop();
                res.add(node.val);
                node = node.right;
            }
        }
 
        return res;
    }
}

重难点

对于递归遍历来说，遍历二叉树代码写起来比较容易，但是递归的过程需要重点理解下。
而对于迭代法来说，弄明白入栈与出栈的过程就基本可以明白，可以通过模拟过程来理解，而中序遍历与前、后序遍历不太一样，需要着重理解了。

附：学习资料链接