numpy.meshgrid()理解

本文的目的是记录meshgrid()的理解过程:

step1. 通过一个示例引入创建网格点矩阵;

step2. 基于步骤1，说明meshgrid()的作用;

step3. 详细解读meshgrid()的官网定义;

说明:step1和2 的数据都是基于笛卡尔坐标系的矩阵，目的是为了方便讨论。

 

step1. 通过一个示例引入创建网格点矩阵;

示例1，创建一个2行3列的网格点矩阵。

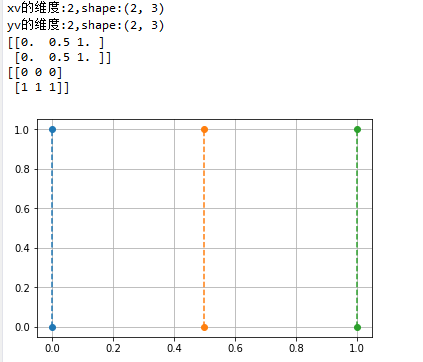
#!/usr/bin/env python3
#-*- coding:utf-8 -*-
############################
#File Name: meshgrid1.py
#Brief:
#Author: frank
#Mail: frank0903@aliyun.com
#Created Time:2018-06-14 21:33:14
############################
import numpy as np
import matplotlib.pyplot as plt

X = np.array([[0, 0.5, 1],[0, 0.5, 1]])
print("X的维度:{},shape:{}".format(X.ndim, X.shape))
Y = np.array([[0, 0, 0],[1, 1, 1]])
print("Y的维度:{},shape:{}".format(Y.ndim, Y.shape))

plt.plot(X, Y, 'o--')
plt.grid(True)
plt.show()

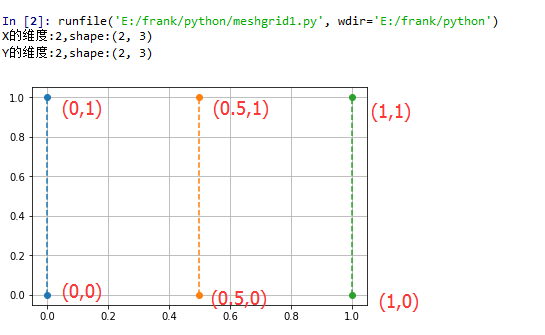
X矩阵是:[[0. 0.5 1. ], [0. 0.5 1. ]]

Y矩阵是:[[0 0 0],[1 1 1]]

 

step2. meshgrid()的作用;

当要描绘的 矩阵网格点的数据量小的时候，可以用上述方法构造网格点坐标数据;
但是如果是一个(256, 100)的整数矩阵网格,要怎样构造数据呢?
方法1:将x轴上的100个整数点组成的行向量，重复256次，构成shape(256,100)的X矩阵;将y轴上的256个整数点组成列向量,重复100次构成shape(256,100)的Y矩阵
显然方法1的数据构造过程很繁琐,也不方便调用,那么有没有更好的办法呢?of course!!!
那么meshgrid()就显示出它的作用了
使用meshgrid方法，你只需要构造一个表示x轴上的坐标的向量和一个表示y轴上的坐标的向量;然后作为参数给到meshgrid(),该函数就会返回相应维度的两个矩阵;
例如,你想构造一个2行3列的矩阵网格点,那么x生成一个shape(3,)的向量,y生成一个shape(2,)的向量,将x,y传入meshgrid(),最后返回的X,Y矩阵的shape(2,3)

 

示例2，使用meshgrid()生成step1中的网格点矩阵

x = np.array([0, 0.5, 1])
y = np.array([0,1])

xv,yv = np.meshgrid(x, y)
print("xv的维度:{},shape:{}".format(xv.ndim, xv.shape))
print("yv的维度:{},shape:{}".format(yv.ndim, yv.shape))

plt.plot(xv, yv, 'o--')
plt.grid(True)
plt.show()

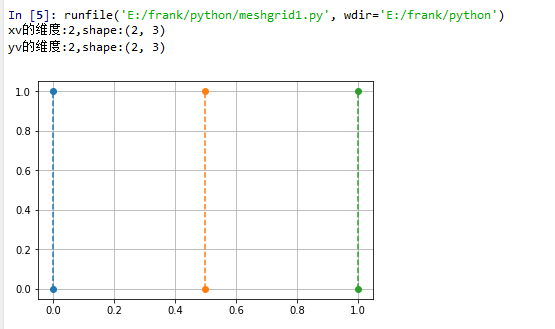
示例3，生成一个20行30列的网格点矩阵

x = np.linspace(0,500,30)
print("x的维度:{},shape:{}".format(x.ndim, x.shape))
print(x)
y = np.linspace(0,500,20)
print("y的维度:{},shape:{}".format(y.ndim, y.shape))
print(y)

xv,yv = np.meshgrid(x, y)
print("xv的维度:{},shape:{}".format(xv.ndim, xv.shape))
print("yv的维度:{},shape:{}".format(yv.ndim, yv.shape))

plt.plot(xv, yv, '.')
plt.grid(True)
plt.show()

 

 step3. 详细解读meshgrid()的官网定义;

numpy.meshgrid(*xi, **kwargs)
Return coordinate matrices from coordinate vectors.
根据输入的坐标向量生成对应的坐标矩阵

Parameters:
　　x1, x2,…, xn : array_like
　　　　1-D arrays representing the coordinates of a grid.
　　indexing : {‘xy’, ‘ij’}, optional
　　　　Cartesian (‘xy’, default) or matrix (‘ij’) indexing of output. See Notes for more details.
　　sparse : bool, optional
　　　　If True a sparse grid is returned in order to conserve memory. Default is False.
　　copy : bool, optional
　　　　If False, a view into the original arrays are returned in order to conserve memory.
　　　　Default is True. Please note that sparse=False, copy=False will likely return non-contiguous arrays.
　　　　Furthermore, more than one element of a broadcast array may refer to a single memory location.
　　　　If you need to write to the arrays, make copies first.
Returns:
　　X1, X2,…, XN : ndarray
　　　　For vectors x1, x2,…, ‘xn’ with lengths Ni=len(xi) ,
　　　　return (N1, N2, N3,...Nn) shaped arrays if indexing=’ij’
　　　　or (N2, N1, N3,...Nn) shaped arrays if indexing=’xy’
　　　　with the elements of xi repeated to fill the matrix along the first dimension for x1, the second for x2 and so on.

 

 针对indexing参数的说明:

indexing只是影响meshgrid()函数返回的矩阵的表示形式，但并不影响坐标点

x = np.array([0, 0.5, 1])
y = np.array([0,1])

xv,yv = np.meshgrid(x, y)
print("xv的维度:{},shape:{}".format(xv.ndim, xv.shape))
print("yv的维度:{},shape:{}".format(yv.ndim, yv.shape))
print(xv)
print(yv)

plt.plot(xv, yv, 'o--')
plt.grid(True)
plt.show()

 

x = np.array([0, 0.5, 1])
y = np.array([0,1])

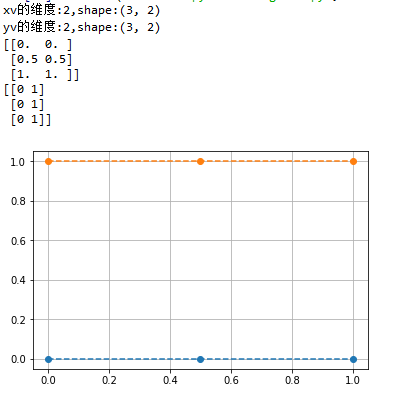
xv,yv = np.meshgrid(x, y,indexing='ij')
print("xv的维度:{},shape:{}".format(xv.ndim, xv.shape))
print("yv的维度:{},shape:{}".format(yv.ndim, yv.shape))
print(xv)
print(yv)

plt.plot(xv, yv, 'o--')
plt.grid(True)
plt.show()