1.学习总结
图的结构是任意两个数据对象之间都可能存在某种特定关系的数据结构,其包含了图的存储结构(邻接矩阵,邻接表),图的遍历(深度优先搜索,广度优先搜索),最小生成树(Prim算法,Kruskal算法),最短路径(Dijkstra算法,Floyd算法),拓扑排序,AOE网与关键路径的内容。
1.1图的思维导图
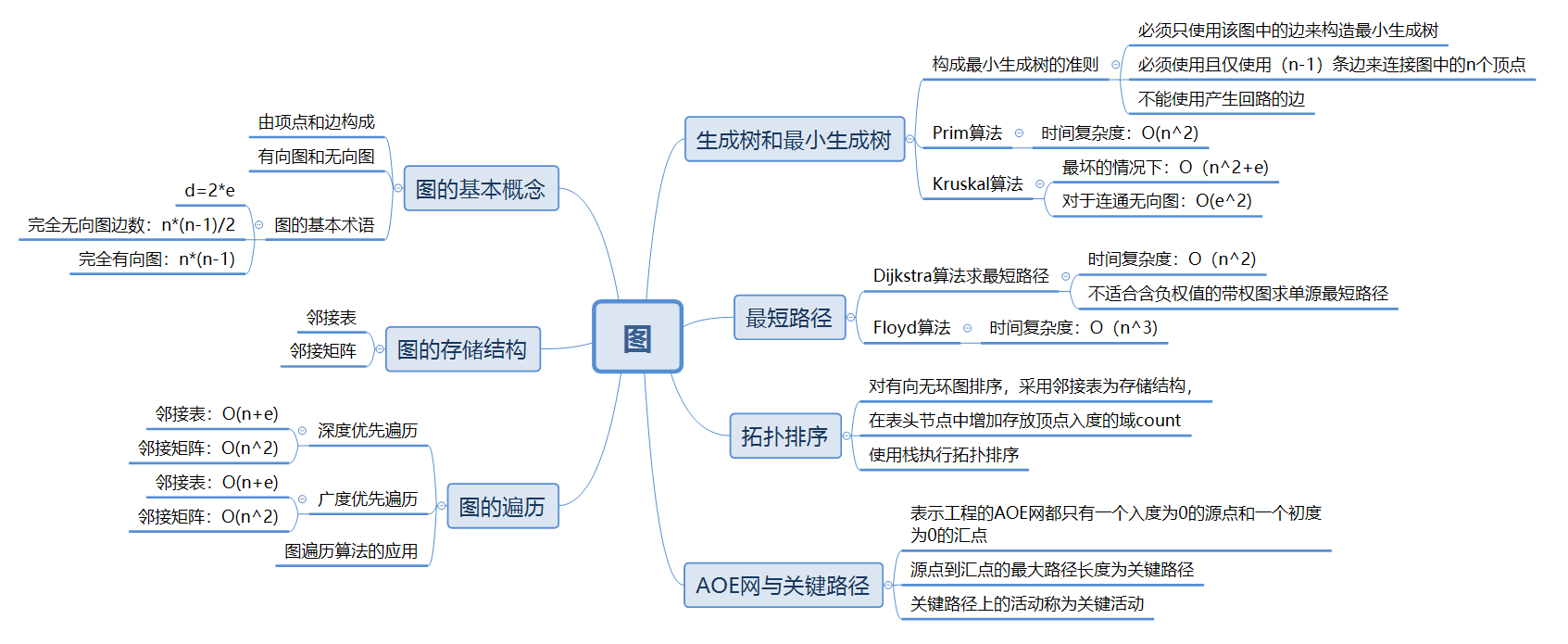
1.2 图结构学习体会
- 深度遍历算法:深度遍历类似于树的先根遍历,是树的先根遍历的推广。其实质是运用了递归思想,在遍历图时,对每个顶点至多调用一次深度遍历函数。
- 广度遍历算法: 广度遍历类似于树的层次遍历。其运用了队列的特点,每个顶点至多进一次队列,遍历图实质上是通过对边或弧找领接点。与深度遍历的时间复杂度相同,只是对顶点访问的顺序不同。
- Prim和Kruscal算法:Prim算法是直接寻找邻边的最小权值,而Kruscal算法需要先对权值大小进行排序后再查找。Kruscal算法的效率要高于Prim算法。
- Dijkstra算法:该算法采用贪心策略,使用广度优先搜索解决有向或无向带权图的单源最短路径问题。
- 拓扑排序算法:只能对有向无环图进行排序,通过对无前驱顶点删除其后继的弧,重复该步骤,直至所有顶点都输出或不存在无前驱顶点为止,可通过其来判断图是否有环。
2.PTA实验作业
2.1 题目1:图着色问题
2.2 设计思路(伪代码)
1.输入n,e,k为节点数、边数和颜色数;
2.建图,利用循环输入代表两个邻接边的x,y;
3.输入要判断的第n 行;
4.比较要用的颜色与提供的颜色,如果不等,则输出NO;
5.如果是非Judge函数,则输出No;
6.若Judge函数返回ture,则输出Yes;
2.3 代码截图

2.4 PTA提交列表说明

编译器选择错误导致编译错误,函数传参数时出现错误,经同学帮忙一起纠正了错误。
2.1 题目2:公路村村通
2.2 设计思路(伪代码)
输入n和m,建立邻接矩阵,并赋初值;
两邻接点间赋权值;
利用prim算法找到最小生成树;
输出最最低成本sumlen;
如果输入数据不足以保证畅通,则输出−1;
2.3 代码截图

2.4 PTA提交列表说明。

编译器选择不正确,参考网上的代码完成。
2.1 题目3:六度空间
2.2 设计思路(伪代码)
1.输入v,e分别代表节点数和边数;
2. 建图,输入每条边直接连通的两个结点的编号;
3.将v赋给总结点数n,让符合条件的节点数m等于用BFS函数计算出的每个节点距离不超过6的节点数;
4.利用m/n*100输出结果;
2.3 代码截图
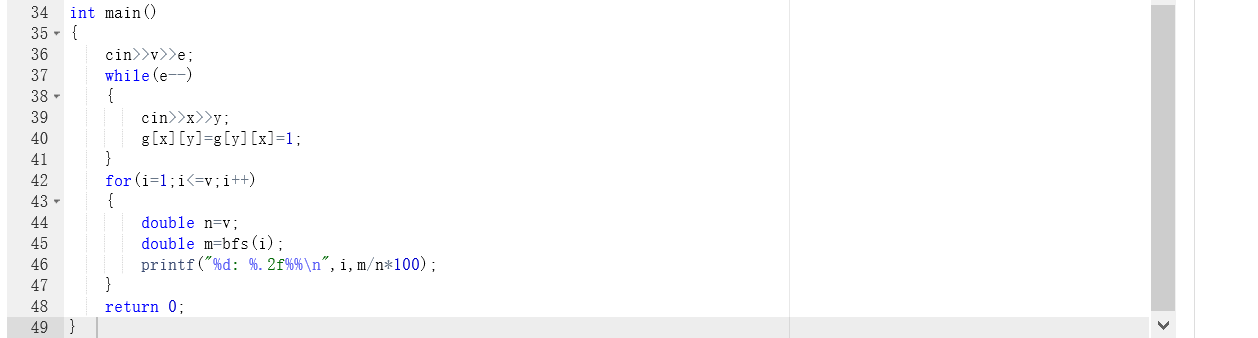
2.4 PTA提交列表说明。

对题目理解不够周全,思路有缺陷,改变思路方向后,参考同学代码才完成。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:165
4. 阅读代码
//邻接表的深度递归算法void DFS(GraphList g, int i){ EdgeNode *p; visited[i] = TRUE; printf("%c ", g->adjList[i].data); //打印顶点,也可以其他操作 p = g->adjList[i].firstedge; while(p) { if(!visited[p->adjvex]) { DFS(g, p->adjvex); //对访问的邻接顶点递归调用 } p = p->next; }}//邻接表的深度遍历操作void DFSTraverse(GraphList g){ int i; for(i = 0; i < g.numVertexes; i++) { visited[i] = FALSE; } for(i = 0; i < g.numVertexes; i++) { if(!visited[i]) { DFS(g, i); } }} |
相比于邻接矩阵存储结构的深度优先遍历算法,对于n个顶点e条边的图来说,邻接矩阵由于是二维数组,要查找某个顶点的邻接点需要访问矩阵中的所有元素,因为需要O(n2)的时间。而邻接表做存储结构时,找邻接点所需的时间取决于顶点和边的数量,所以是O(n+e)。显然对于点多边少的稀疏图来说,邻接表结构使得算法在时间效率上大大提高。


