算法实验
多机调度问题(贪心法)
问题描述
有n个独立的作业由m台相同的机器进行加工处理,作业i所需的处理时间为t (1≤i≤n),每个作业均可在任何一台机器上加工处理,但不可间断、拆分。多机调度问题要求给出种作业调度方案,使所给出的n个作业在尽可能短的时间内由m台机器加工处理完成。
例如,7个独立的作业由3台机器加工处理,各作业的处理时间为{2, 14, 4, 6,16, 5, 3}。最短完成时间为17, 3台机器的作业调度分别为: 机器1:{16}; 机器2:{14, 3}; 机器3:{6, 5, 4, 2}
设计最优贪心策略,给出C语言代码求解多机调度问题并分析时间复杂度。
解决方案
首先将作业按照其所需时间从大到小降序排序,然后遍历该数组,比较M台机器当前的运行时间,将作业相应的调度到其中运行时间最少的机器上,重复这一步,直到所有作业调度完最后再输出每台机器的分配情况以及各机器的运行总时长。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define MACHINE_NUM 3
void MultiScheduling(vector<vector<int>>& works, vector<vector<pair<int, int>>>& arrange, vector<int>& runTime) {
if (MACHINE_NUM >= works.size()) {
//机器数目大于等于作业个数时直接分配
for (int i = 0; i < works.size(); i++) {
auto work = make_pair(works[i][0], works[i][1]);
arrange[i].push_back(work);
runTime[i] = works[i][1];
}
return;
}
sort(works.begin(), works.end(),
[](vector<int>& a, vector<int>& b) ->bool {
return a[1] > b[1];
});
//按照作业所需时间降序排序
int curMinTimeIndex = 0;
//最小运行时间的机器编号
for (int i = 0; i < works.size(); ++i) {
curMinTimeIndex = min_element(runTime.begin(), runTime.end()) - runTime.begin();
runTime[curMinTimeIndex] += works[i][1];
//机器执行作业的时间
arrange[curMinTimeIndex].push_back({ make_pair(works[i][0],works[i][1]) });
//第i个作业被分配的情况
}
}
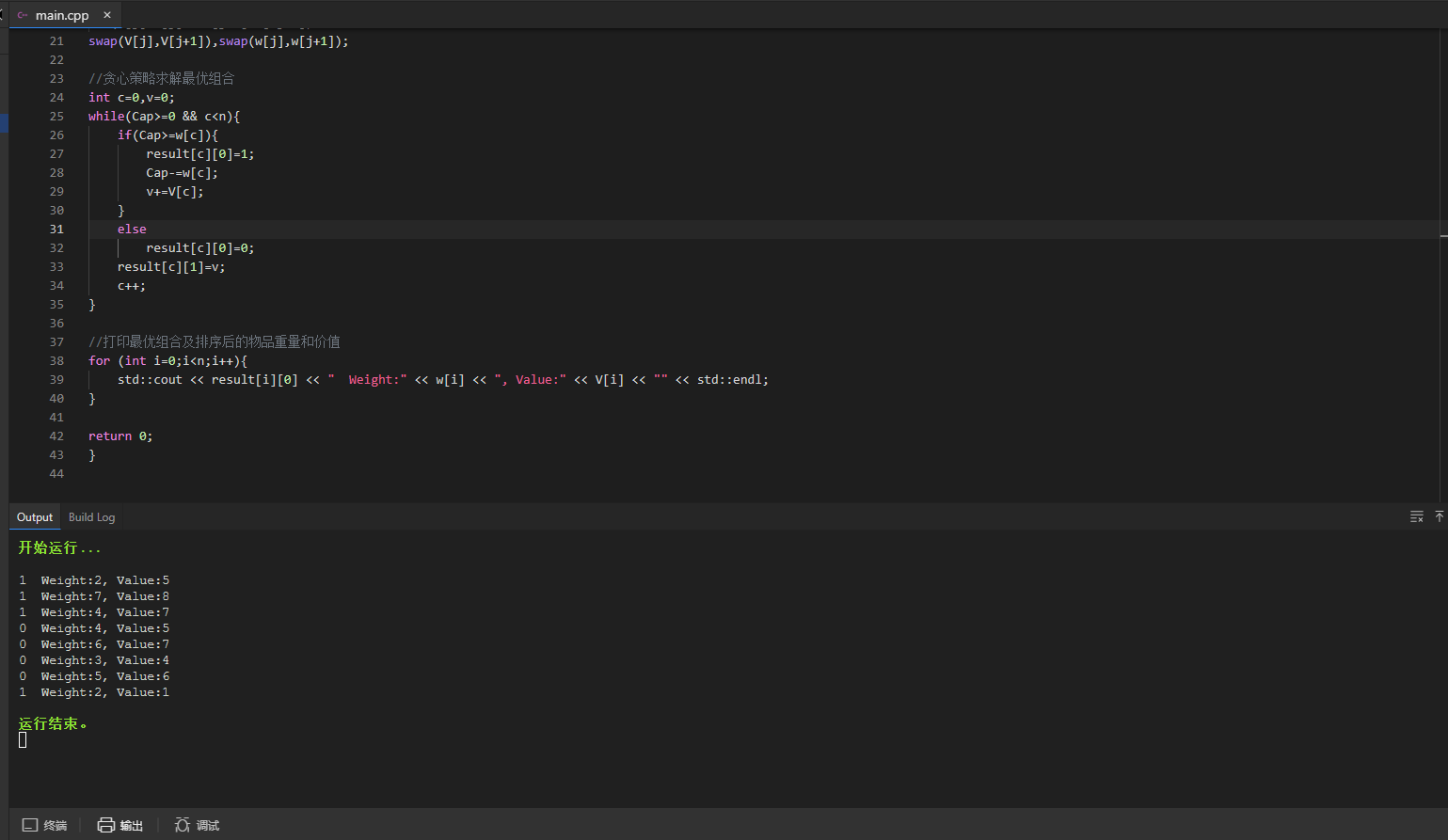
//打印每台机器被调度之后的结果
void Print(vector<vector<pair<int, int>>>& arrange, vector<int>& runTime) {
for (int i = 0; i < arrange.size(); i++) {
cout << "第" << i + 1 << "台机器的作业: " << endl;
for (int j = 0; j < arrange[i].size(); j++) {
cout << arrange[i][j].first << "号作业时长: "
<< arrange[i][j].second << "h" << endl;
}
cout << "第" << i + 1 << "台机器总运行时长: "
<< runTime[i] << endl << endl;
}
}
int main() {
vector<vector<int>> works{
{1,2},{2,14},{3,4},{4,6},{5,16},{6,5},{7,3}
// 将7个作业依次从1到7命名组成数组
};
vector<vector<pair<int, int>>> arrange(MACHINE_NUM);
//记录每台机器全部作业时间
vector<int> runTime(MACHINE_NUM, 0);
MultiScheduling(works, arrange, runTime);
Print(arrange, runTime);
return 0;
}
时间复杂度为
O(nlogn)
结果:
0-1背包问题(贪心法)
问题描述
请你设计多种贪心策略,给出每种可能的C语言代码并对比结果,得到0-1背包问题的近似最优解。
给定n个物品和一个容量为C的背包,物品i的重量是wi,其价值是vi, 0-1 背包问题要求从这n个物品中,选择装入背包的最优组合( 物品不可以分割),使得装入背包中的物品的总价值最大。
例如,将8件物品放入容量为15的背包,8件物品的重量和价值分别为:
w={7, 4, 4, 6,2,2,3,5}
V={8, 7,5,7,1,5,4,6}
解决方法
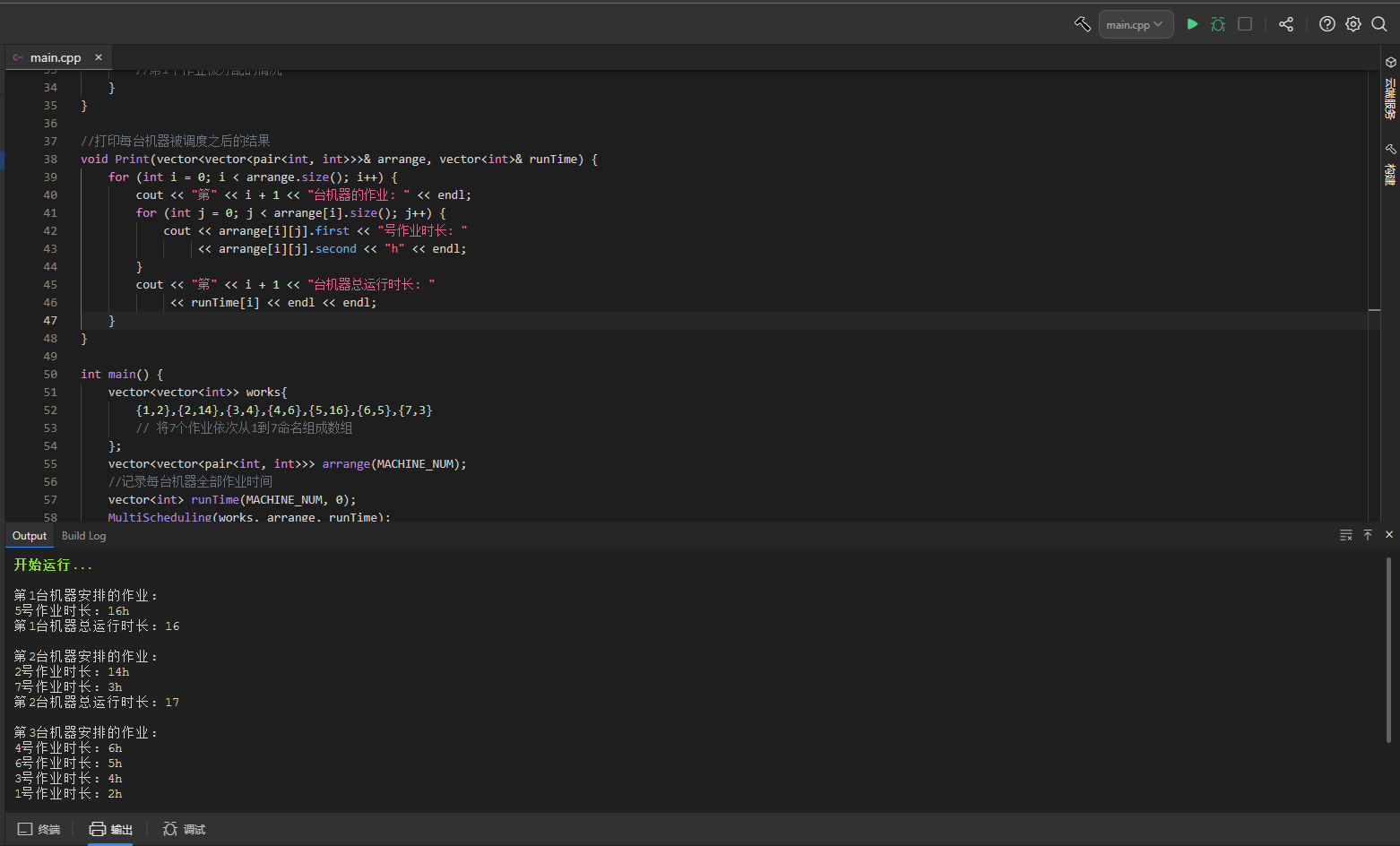
第一种:按重量排序
对于给定物品,按物品重量从小到大排序,再采用贪心选择法,依次选择重量小的物品放入背包,直到背包装不下为止;
#include <stdio.h>
int main() {
int n=8,m;
int w[8]={7,4,4,6,2,2,3,5};
int v[8]={8,7,5,7,1,5,4,6};
// 按重量排序
for(int i=0;i<n;i++){
for(int j=0;j< n-1-i;j++){
if(w[j]>w[j+1]) {
int temp = w[j];
w[j] = w[j+1];
w[j+1] = temp;
temp = v[j];
v[j] = v[j+1];
v[j+1] = temp;
}
}
}
printf("The result is:\n");
for(int i=0;i<n;i++){
printf("%d %d\n",w[i],v[i]);
}
return 0;
}
结果输出:
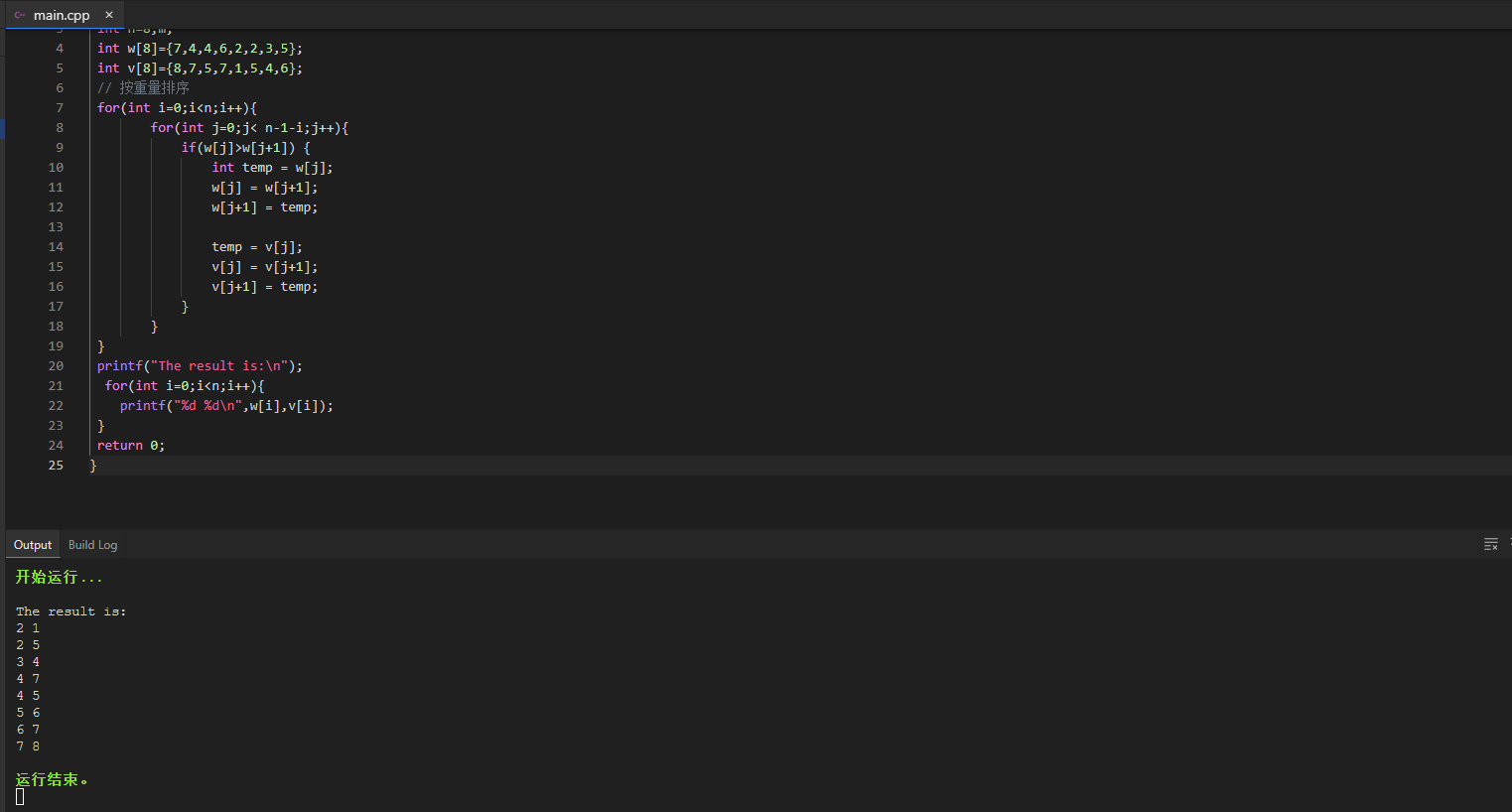
第二种:按价值排序
对于给定物品,按物品的价值从大到小排序,再采用贪心选择法,依次选择价值高的物品放入背包,直到背包装不下为止;
#include<iostream>
using namespace std;
int main()
{
int w[] = {7, 4, 4, 6,2,2,3,5};
int v[] = {8, 7,5,7,1,5,4,6};
for(int i = 0; i < 8; i++) {
int count = 1;
for(int j=i+1; j<8; j++) {
if(w[j] == w[i]) {
v[i] += count;
count++;
}
}
}
for(int i=0; i<8; i++) {
cout << w[i] << " " << v[i] << endl;
}
cout << endl;
return 0;
}
结果输出:
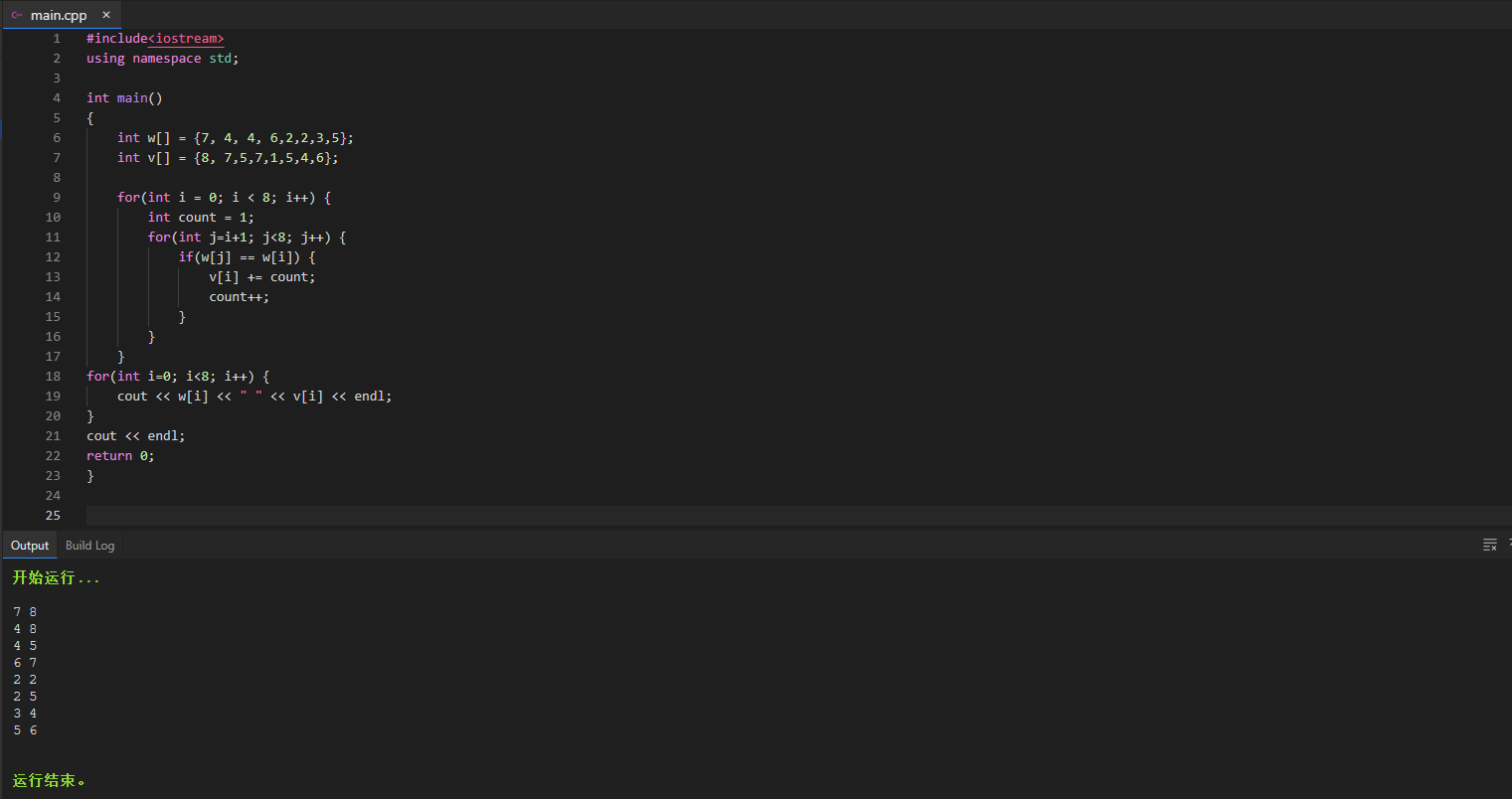
第三种:按单位重量排序
先使用swap()函数对物品重量和物品价值进行排序,之后从剩余的背包容量中选择单位重量最高的物品,直到背包所剩容量不够放物品为止。最后返回最优组合以及排序后的物品重量和价值。
#include<iostream>
void swap(int &a, int &b) {
int temp;
temp = a;
a= b;
b = temp;
}
int main() {
int n = 8;
int w[8] = {7, 4, 4, 6, 2, 2, 3, 5};
int V[8] = {8, 7, 5, 7, 1, 5, 4, 6};
int Cap = 15;
int result[8][2]; //最优组合
//依据单位重量排序
for(int i=0;i<n-1;i++)
for(int j=0;j<n-1-i;j++)
if(V[j]/w[j] < V[j+1]/w[ j+1])
swap(V[j],V[j+1]),swap(w[j],w[j+1]);
//最优组合
int c=0,v=0;
while(Cap>=0 && c<n){
if(Cap>=w[c]){
result[c][0]=1;
Cap-=w[c];
v+=V[c];
}
else
result[c][0]=0;
result[c][1]=v;
c++;
}
//最优组合及排序后的物品重量和价值
for (int i=0;i<n;i++){
std::cout << result[i][0] << " Weight:" << w[i] << ", Value:" << V[i] << "" << std::endl;
}
return 0;
}
结果输出: