201971010131-李治江 实验二 个人项目—{01背包问题}项目报告
| 项目 | 内容 |
|---|---|
| 课程班级链接 | 19卓越 |
| 作业要求链接 | 作业要求 |
| 我的课程学习目标 | 掌握PSP流程进行软件开发;学会使用GitHub发布软件项目 |
| 这个作业在哪些方面帮助我实现学习目标 | 更加巩固了之前学过的贪心法、动态规划法以及回溯法; |
| GitHub仓库链接 | 仓库 |
任务一
作业点评链接:
点评链接一:201971010146-杨凯 实验一 软件工程准备
点评链接二:201971010135-孙得弘 实验一 软件工程准备—熟悉博客园操作以及对课程的思考
点评链接三:201971010145-姚恪 实验一 软件工程准备
任务二
总结详细阅读《构建之法》第1章、第2章,掌握PSP流程
第一章:
1.通过第一章主要了解了什么是软件工程,即软件=程序+软件工程。
2.
- 软件的特殊性:
- 复杂性
- 不可见性
- 易变性
- 服从性
- 非连续性。
3.软件工程是一门研究用工程化方法构建和维护有效的、实用的和高质量的软件的学科。
4.它涉及到程序设计语言,数据库,软件开发工具,系统平台,标准,设计模式等方面。
第二章:
PSP是一种可用于控制、管理和改进个人工作方式的自我持续改进过程,是一个包括软件开发表格、指南和规程的结构化框架。
PSP能够说明个体软件过程的原则;确定软件工程师为改善产品质量要采取的步骤;帮助软件工程师作出准确的计划;建立度量个体软件过程改善的基准;确定过程的改变对软件工程师能力的影响。
PSP
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 10 | 10 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 15 | 10 |
| Development | 开发 | 400 | 450 |
| Analysis | 需求分析 (包括学习新技术) | 6 | 3 |
| Design Spec | 生成设计文档 | 10 | 8 |
| Design Review | 设计复审 (和同事审核设计文档) | 15 | 10 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 20 | 10 |
| Design | 具体设计 | 15 | 20 |
| Coding | 具体编码 | 180 | 220 |
| Code Review | 代码复审 | 30 | 35 |
| Test | 测试(自我测试,修改代码,提交修改) | 30 | 45 |
| Reporting | 报告 | 40 | 40 |
| Test Report | 测试报告 | 30 | 30 |
| Size Measurement | 计算工作量 | 25 | 15 |
| Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 30 | 20 |
任务三 项目开发
任务描述:
- 背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
{0-1}KP数据集是研究{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解{0-1}背包问题的经典算法。
功能设计
- 可正确读入实验数据文件的有效{0-1}KP数据;
- 能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图;
- 能够对一组{0-1}KP数据按重量比进行非递增排序;
- 用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位);
- 任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
流程图
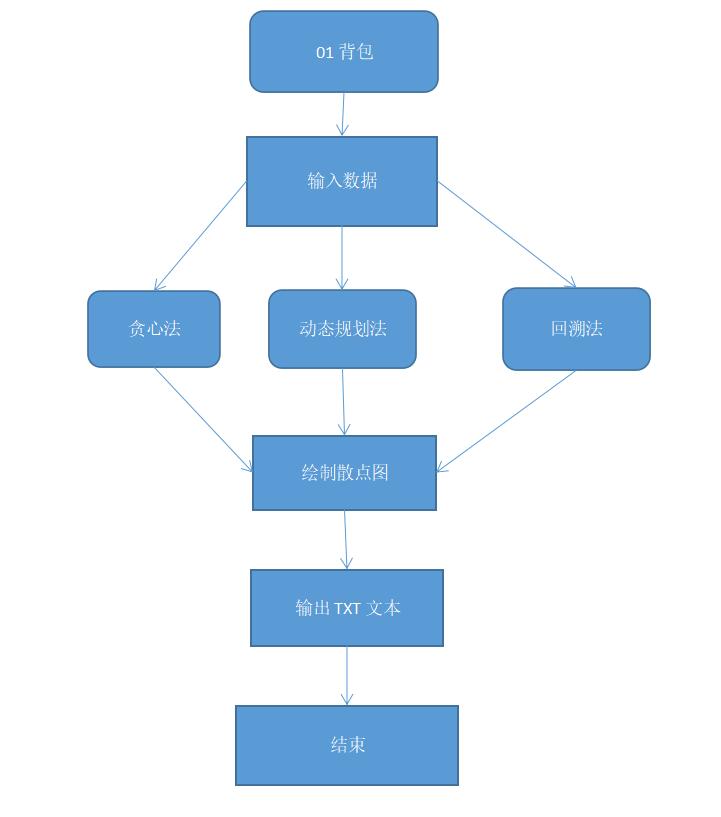
代码
- 动态规划
int KnapSack1(int n,goods a[],int C,int x[])
{
int j;
int V[N][10*N];
for(int i=0;i<=n;i++) //初始化第0列
V[i][0]=0;
for(int j=0;j<=C;j++) //初始化第0行
V[0][j]=0;
for(int i=1;i<=n;i++) //计算第i行,进行第i次迭代
for(int j=1;j<=C;j++)
if(j<a[i-1].w)
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-a[i-1].w]+a[i-1].p);
j=C; //求装入背包的物品
for (int i=n;i>0;i--)
{
if (V[i][j]>V[i-1][j]){
x[i-1]=1;
j=j-a[i-1].w;
}
else x[i-1]=0;
}
return V[n][C]; //返回背包取得的最大价值
}
- 回溯法
int BackTrack(int i)
{
if(i>n-1){
if(bestP<cp){
for (int k=0;k<n;k++) X[k]=cx[k];//存储最优路径
bestP=cp;
}
return bestP;
}
if(cw+a[i].w<=C){ //进入左子树
cw=cw+a[i].w;
cp=cp+a[i].p;
cx[a[i].sign]=1; //装入背包
BackTrack(i+1);
cw=cw-a[i].w;
cp=cp-a[i].p; //回溯,进入右子树
}
cx[a[i].sign]=0; //不装入背包
BackTrack(i+1);
return bestP;
}
int KnapSack2(int n,goods a[],int C,int x[])
{
for(int i=0;i<n;i++)
{
x[i]=0;
a[i].sign=i;
}
sort(a,a+n,m);//将各物品按单位重量价值降序排列
BackTrack(0);
return bestP;
}
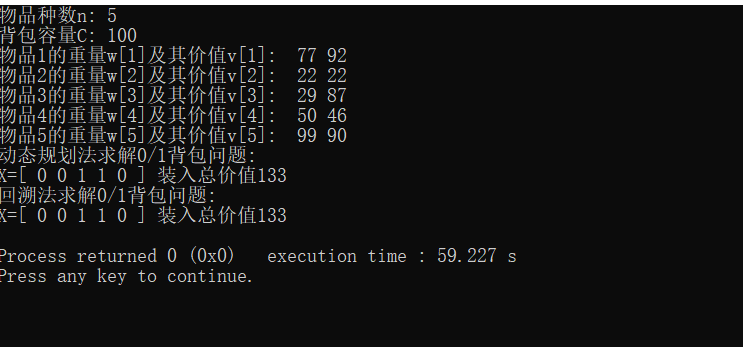
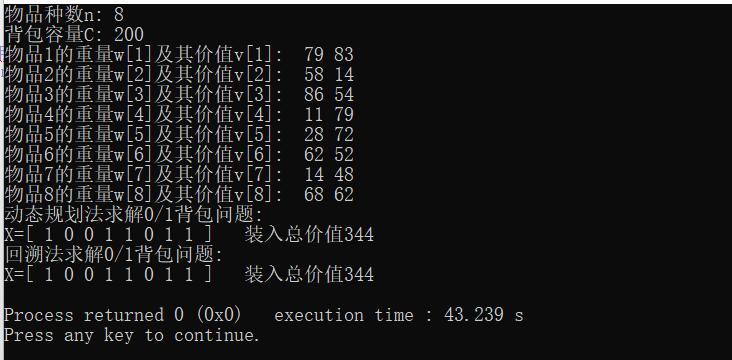
- 运行结果
![]()
![]()
代码规范
| 项目 | 规范 |
|---|---|
| 缩进 | 使用tab 作为缩进 |
| 变量命名 | (1)变量名必须以字母或者下划线开头;(2)不能中英混搭; |
| 每行最大字符 | 单行不超过256个 |
| 常量 | 常量命名全部大写,单词间用下划线隔开 |
| 注释 | (1)行内注释可使用//...形式;(2)函数前部注释需使用/*内容/形式 |
| 空行 | (1)引入头文件其间部分不允许空行;(2) 静态变量/常量定义后跟一空行;(3)每个函数后跟一空行,除非是最后一个函数 |
任务四
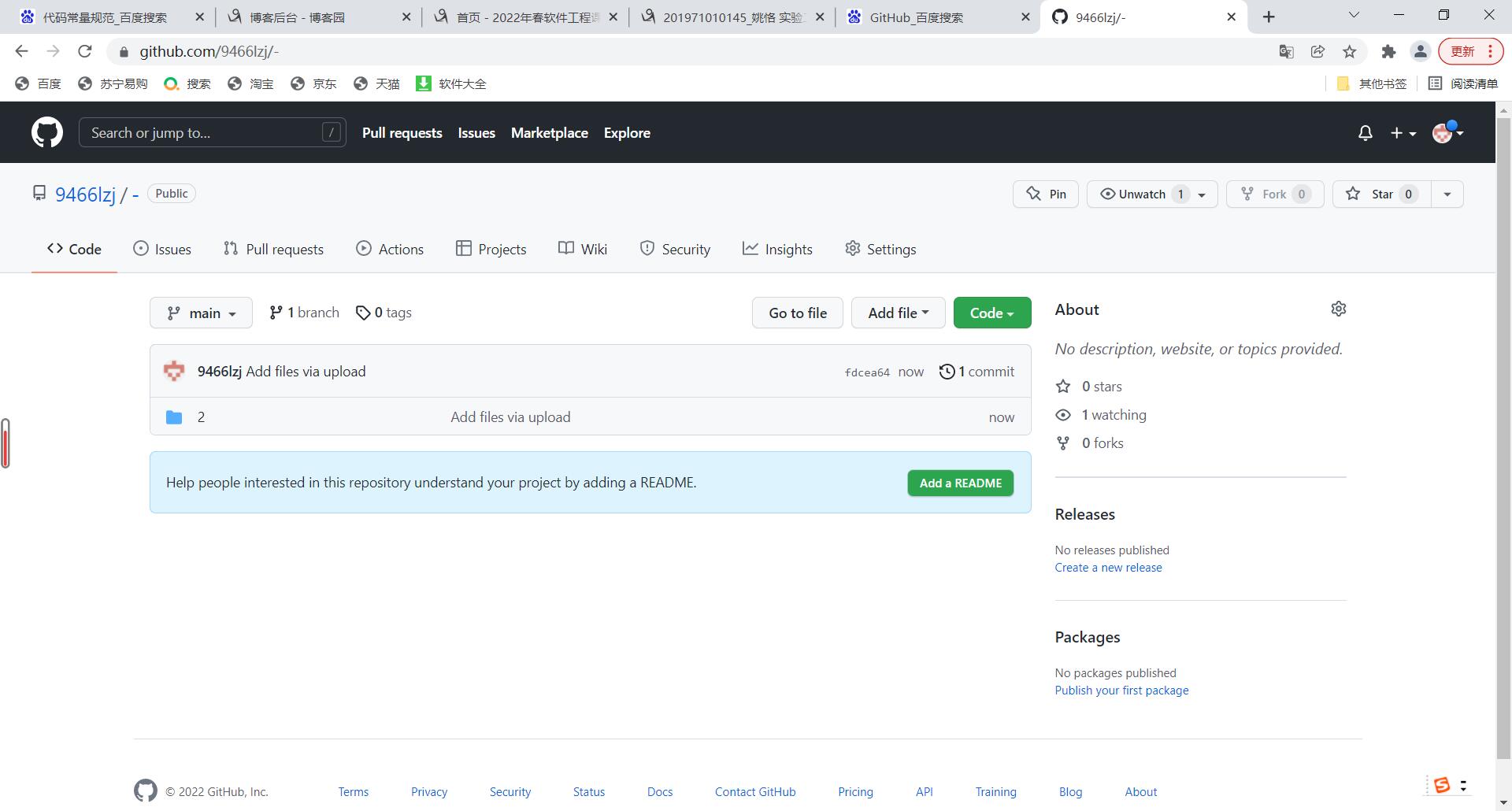
- 完成任务3的程序开发,将项目源码的完整工程文件提交到你注册Github账号的项目仓库中
![]()
心得体会:
- 通过本次的实验,对于上学期所学过的算法又有了新的体会。
- 第一次使用PSP来进行项目开发,使得我比起之前来说无论是代码还是流程都规范了不少,极大地提高了效率。
- 在这次项目中,发现了很多自己以前未曾注意的细节,有很大的提升。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号