【tensorflow】神经网络的优化：指数衰减学习率、过拟合和欠拟合的解决方法、激活函数&损失函数&优化器的选择

神经网络的复杂度

1.空间复杂度

层数 = 隐藏层的层数 + 1个输出层

总参数 = 总w + 总b

2.时间复杂度

乘加运算次数 = 总w

 

指数衰减学习率

学习率lr表征了参数每次更新的幅度，设置过小，参数更新会很慢，设置过大，参数不容易收敛。

 

 

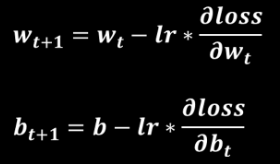
在实际应用中，可以先使用较大学习率，快速找到较优值，然后逐步减小学习率，使模型找到最优解。

比如，指数衰减学习率。

指数衰减学习率 = 初始学习率 * 学习率衰减率^^{(当前轮数/多少轮衰减一次)}

• 初始学习率：最初设置的学习率。
• 学习率衰减率：学习率按照这个比例指数衰减。
• 当前轮数：可以用 epoch 表示（当前迭代了多少次数据集），也可以用 step 表示（当前迭代了多少次batch）。
• 多少轮衰减一次：迭代多少次更新一次学习率，决定了学习率更新的频率。

# 例：
# 数据集迭代次数
epoch = 50
# 初始学习率
lr_base = 0.2
# 学习率衰减率
lr_decay = 0.99
# 多少轮衰减一次
lr_step = 1

for epoch in range(epoch):
    # 指数衰减学习率
    lr = lr_base * lr_decay ** (epoch/lr_step)
    
    # 参数求导
    with tf.GradientTape() as tape:
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)

    # 参数自更新
    w.assign_sub(lr * grads)

 

激活函数

线性函数表达力不够，加入非线性函数(激活函数)，使得神经网络可以随层数的增加提升表达力。

 

优秀的激活函数需要满足：

• 非线性：只有当激活函数是非线性时，才不会被单层网络所替代，使多层网络有了意义。
• 可微性：优化器大多使用梯度下降法更新参数，若激活函数不可微（不可求导），就不能更新参数。
• 单调性：当激活函数是单调的，能保证单层网络的损失函数是凸函数，更容易收敛。
• 近似恒等性：f(x) ≈ x，这样的神经网络更稳定。

 

激活函数输出值

• 如果激活函数的输出是有限值，权重对特征的影响会更显著，用梯度下降的方法更新参数会更稳定。
• 如果激活函数的输出是无限值，参数的初始值对模型的影响非常大，建议使用更小的学习率。

 

几种常见的激活函数

Sigmoid 激活函数

tf.nn.sigmoid(x)

Tanh 激活函数

tf.nn.tanh(x)

Relu 激活函数

tf.nn.relu(x)

Leaky Relu 激活函数

tf.nn.leaky_relu(x)

 

对初学者的建议：

• 首选 relu 激活函数。
• 学习率设置较小值。
• 输入特征标准化，即让输入特征满足以0为均值，1为标准差的正态分布。
• 初始参数中心化，即让随机生成的参数满足以0为均值，√(2/当前层输入特征个数) 为标差的正态分布。

 

损失函数loss

损失函数，即前向传播预测结果 y 与已知标准答案 y_ 的差距。

神经网络的优化目标就是找到某套参数，使得预测结果与标准答案无限接近,即 loss 值最小。

 

主流loss有三种：

均方误差

loss = tf.reduce_mean(tf.square(y_ - y))

自定义

loss = tf.reduce_mean(tf.where(条件语句, 真返回A, 假返回B))

交叉熵

交叉熵越大，两个概率分布越远

交叉熵越小，两个概率分布越近

y_pro = y.nn.softmax(y)

tf.losses.categorical_crossentropy(y_, y_pro)

执行分类问题时，通常先用 softmax 函数使输出结果符合概率分布，再求交叉熵损失函数。

tensorflow给出了同时计算概率分布和交叉熵的函数：

tf.nn.softmax_cross_entropy_with_logits(y_, y)

 

欠拟合与过拟合

欠拟合：模型不能有效拟合数据集，对现有数据集学习不够彻底。

过拟合：模型对数据拟合太好，但对新数据难以做出判断，缺乏泛化力。

 

 

网络训练过程中会遇到的情况：

loss 是训练集的损失值，val_loss 是测试集的损失值。

loss 不断下降，val_loss 不断下降：网络仍在学习;（最好情况）

loss 不断下降，val_loss 趋于不变：网络过拟合;（增大数据集 || 正则化）

loss 趋于不变，val_loss 不断下降：数据集有问题;（检查dataset）

loss 趋于不变，val_loss 趋于不变：学习遇到瓶颈;（减少学习率 || 减少批量数目）

loss 不断上升，val_loss 不断上升：网络结构设计或训练超参数设置不当，数据集经过清洗等问题。（最坏情况）

 

欠拟合的解决方法：

• 增加输入特征项
• 增加网络参数
• 减少正则化参数

 

过拟合的解决方法：

• 数据清洗
• 增大训练集
• 采用正则化
• 增大正则化参数

 

正则化减少过拟合：

正则化，就是在损失函数中引入模型复杂度指标，给每个参数 w 加上权重，抑制训练中的噪声。

正则化通常只对参数 w 使用，不对偏置 b 使用。

loss = loss(y_, y) + regularizer * loss(w)

loss(y_, y):以前求得的 loss 值。

regularizer：参数 w 在总 loss 中的比重.

loss(w)：

• 对所有参数 w 求和（L1正则化：大概率会使很多参数变为0，可用来稀疏参数，降低模型复杂度）
• 对所有参数 w 的平方求和（L2正则化：会使参数接近0但不等于0，可用来减小参数的数值，有效缓解数据集中因噪声引起的过拟合）

 

# 例：
with tf.GradientTape() as tape:

    ...

    # 原始 loss
    loss_mse = tf.reduce_mean(tf.square(y_ - y))
    # 用来寄存所有参数 w L2正则化后的结果
    loss_regularization = []

    # 将所有参数 w 做 L2正则化处理，并存在loss_regularization中
    loss_regularization.append(tf.nn.l2_loss(w1))
    loss_regularization.append(tf.nn.l2_loss(w2))

    # 计算所有参数 w L2正则化后的总和
    loss_regularization = tf.reduce_sum(loss_regularization)

    # 正则化
    loss = loss_mse + 0.03 * loss_regularization

# 对各参数求导
grads = tape.gradient(loss, [w1, b1, w2, b2])

# 参数自更新
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])

...

 

优化器更新网络参数

 

借鉴博客：

https://www.cnblogs.com/niulang/p/11752605.html