opencv —— Sobel 一阶导数算子、Scharr 滤波器 一阶导数用于边缘检测

sobel 算子的基本概念

sobel 算子是一个主要用于边缘检测的离散微分算子，它结合了高斯平滑和微分求导，用于计算图像灰度函数的近似梯度。

其基础来自于一个事实，即在边缘部分，像素值出现“跳跃”或者较大的变化。如果在此边缘部分求取一阶导数，会看到极值的出现。正如下图所示：

 

 

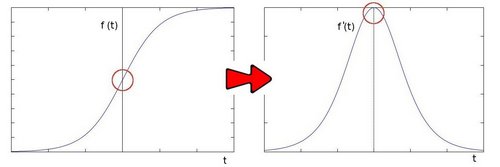
sobel 算子的计算过程

（1）分别在 x 和 y 两个方向求导

x 方向求导：将源图像与 G_x 进行卷积。对竖线敏感（导数大），横线不敏感（导数小）。

y 方向求导：将源图像与 G_y 进行卷积。对竖线不敏感（导数小），横线敏感（导数大）。

（2）对于图像的每一点，结合以上两个结果求出近似梯度

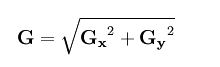
可以简化成：

 

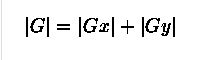
Sobel 函数

void Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize = 3, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT);

• src，输入图像，填 Mat 类型即可。
• dst，输出图像，需要和源图像有一样的尺寸和类型。
• ddepth，输出图像的深度，满足下列要求：

src.depth() = CV_8U, ddepth = -1 / CV_16S / CV_32F / CV_64F

src.depth() = CV_16U / CV_16S, ddepth = -1 / CV_32F / CV_64F

src.depth() = CV_32F, ddepth = -1 / CV_32F / CV_64F

src.depth() = CV_64F, ddepth = -1 / CV_64F

• dx，x 方向上导数的阶数，只能是 0、1、2。若求 x 方向上的一阶导数，dx = 1，dy = 0。
• dy，y 方向上导数的阶数，只能是 0、1、2。若求 y 方向上的一阶导数，dx = 0，dy = 1。
• ksize，默认值为 3，表示 sobel 核的大小，必须取 1、3、5、7。
• scale，计算导数值的缩放因子，默认值为 1，表示默认情况下不进行缩放。
• delta，输出梯度 = scale * G + delta。
• borderType，G_x 和 G_y 都有一定大小，边缘会处理不到，需要进行边缘扩展。这个参数指定边缘扩充类型。

 一般情况下，都是使用 ksize×ksize 内核来计算导数的，然而，当 ksize = 1 时，会使用 3×1、1×3 的内核。这种情况下，并没有进行高斯平滑操作。

代码示例：

#include<opencv.hpp>
using namespace cv;
int main() {
    Mat src = imread("C:/Users/齐明洋/Desktop/证件照/7.jpg");
    GaussianBlur(src, src, Size(3, 3), 0, 0);
    imshow("src", src);

    Mat gray, x_img, y_img, sobel_img;
    cvtColor(src, gray, COLOR_BGR2GRAY);
    Sobel(gray, x_img, -1, 1, 0, 3);
    imshow("x_img", x_img);
    Sobel(gray, y_img, -1, 0, 1, 3);
    imshow("y_img", y_img);

    addWeighted(x_img, 1, y_img, 1, 0, sobel_img);
    //https://www.cnblogs.com/bjxqmy/p/11986135.html
    imshow("sobel_img", sobel_img);
    waitKey(0);
}

效果演示：

 

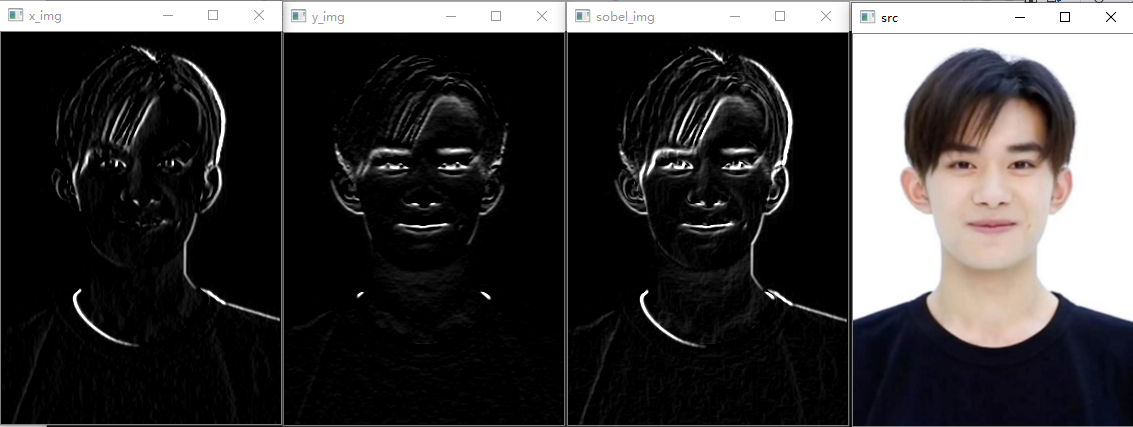
补充说明：当内核大小为 3×3 时，sobel 内核可能产生比较明显的误差，毕竟 sobel 算子只是求取了导数的近似值而已。为解决这一问题，OpenCV 提供了 Scharr 函数，但该函数仅作用于 3×3 的内核。该函数的运算与 Sobel 函数一样快，但结果更精确，其内核为

 

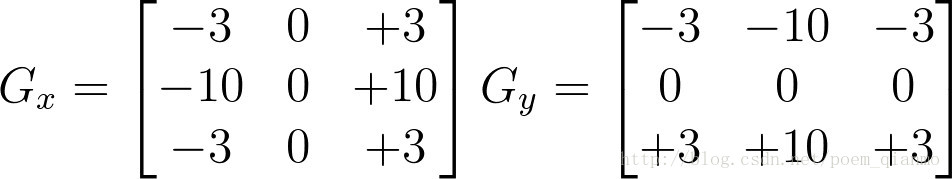
借鉴博客：https://www.cnblogs.com/wxl845235800/p/7700887.html

https://www.cnblogs.com/sevenyuan/p/7874344.html