推荐系统:矩阵分解与邻域的融合模型
推荐系统通常分析过去的事务以建立用户和产品之间的联系,这种方法叫做协同过滤。
协同过滤有两种形式:隐语义模型(LFM),基于邻域的模型(Neighborhood models)。
本篇文章大部分内容为大神Koren的Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model ,这篇文章发表时我还在上初中。文章内容并未过时,主要介绍SVD,SVD++,以及SVD与基于邻域模型的融合。
一、Basic
基于邻域的模型:计算item与item(或者user与user)之间的联系。用户对于一个物品的评分预测主要基于该用户对其他相似物品的评价。这个方法只用到了一个维度,要么item to item,要么user to user。
隐语义模型,例如SVD,用到了item和user两个维度,使他们直接进行比较。隐语义模型尝试解释一些物品的特征,具体可见从SVD到推荐系统。
基于邻域的模型对于检测局部化关系的数据很有效,因为它只依赖于小部分很重要的关系数据,且通常将大部分的用户数据丢掉。相反的是,隐语义模型对于评估整体更有效,它会用到全部的数据,但是这个模型对于预测有强烈联系的小集合数据很不好。
1.1 Baseline
我们把用户符号记为u、v,物品符号为i、j,则\(r_{ui}\)表示用户u对物品i的真实评分。 \(\hat r_{ui}\) 表示用户u对物品i评分的预测值。
很多因素影响着用户的评分,以下三点需要考虑:
- 对于不同平台来说,有的平台评分高,有的平台评分低(如猫眼和豆瓣)
- 在同一个平台上,不同人的评分标准不一样,有的人很严格,有的人很宽容
- 在同一个平台上,不同item的评分平均也不一样,有大众一致认为的好片,也有大众一致认为的渣片(如《肖申克的救赎》和《小时代》)
根据以上三点,一个对用户评分的预测的baseline可以用下式表示:
\(b_{ui}=\mu+b_{u}+b_{i}\)
参数\(\mu\)表示平台的分数平均,参数\(b_{u}\)和\(b_{i}\)分别表示用户与物品的平均程度。举个例子,在某个电影评分平台上,所有电影的评分为3.7,则\(\mu\)为3.7。《泰坦尼克号》比平均电影评分要好,且高了0.5分。Joe是一个不苟言笑的人,俗称critical user,他的所有评分比大众的平均要低0.3。所以Joe对《泰坦尼克号》的评分使用baseline可以预测为3.9分(3.7-0.3+0.5)。为了得到\(b_{u}\)和\(b_{i}\),我们可以尝试解决一下优化问题:
\(min\sum_{(u,i)\in\kappa}(r_{ui}-\mu-b_{u}-b_{i})^2+\lambda_{1}(\sum_{u} b_{u}^2+ \sum_{i} b_{i}^2)\tag{1}\)
这是一个典型问题,第一项为均方误差,第二项为正则化项。
1.2 基于邻域的模型(Basic Neighborhood models)
基于邻域的模型分为两种,一种以用户user为导向,评分预测基于识别与该用户相类似的其他用户。另一种以物品item为导向,评分预测基于物品之间的相似度。相似度的相关计算可以看我的这篇博客推荐系统中物品相似度计算。在文章中,我们关注以item为导向的预测模型。
我们通常来 统计喜欢两个不同物品的人数交集 计算物品的相似度,如pearson相似度,用\(\rho_{ij}\)表示。但是有一些统计的计算只依赖于一小部分数据集合(如两个很冷门的电影,只被小部分专业人士同时看过),那么,这样的统计就不具有代表性了。这时,我们可以添加一个惩罚,即:
\(s_{ij}=\frac{n_{ij}}{n_{ij}+\lambda_{2}}\rho_{ij}\tag{2}\)
参数\(n_{ij}\)表示同时喜欢物品i和j的人数。可以看到,当n小的时候,与\(\lambda_{2}\)(通常为100)同数量级或小于它,相似度会收到缩减的惩罚。如果n非常大,则没有惩罚。
我们的目标是预测\(r_{ui}\),即用户u没有评分过的物品i。根据物品相似度,我们提取与物品i最相似的k个的物品(用户u有过评分的),并将这k个物品的集合表示为\(S^{k}(i;u)\)。那么我们的预测\(\hat r_{ui}\)则为在baseline的基础上,加上k个物品的加权平均,即:
\(\hat r_{ui}=b_{ui}+\frac {\sum_{j\in S^{k}(i;u)}s_{ij}(r_{uj}-b_{uj})}{\sum_{j\in S^{k}(i;u)}s_{ij}}\tag{3}\)
但是,(3)式的方法存在几个问题:
- 这个方法不能被正式的模型证明
- 两个物品之间的相似度的衡量在没有考虑整个邻域集的相互作用下是否适合
- (3)式中权重的计算方法太依赖于邻域集,但是有的物品可能邻域集为空(如用户u没有对与物品i相似的任何物品有过评分)。
所以,为了克服以上三点,我们采用的以下学习方法:
\(\hat r_{ui}=b_{ui}+\sum_{j\in S^{k}(i;u)}\theta_{ij}^u(r_{uj}-b_{uj})\)
这里的插入权重\(\theta_{ij}^u\)不是一个个单独计算的,而是依赖于许多邻项的交叉,这是一个统计数,而不是学习得到的。(By globally solving a suitable optimization problem, this simultaneous interpolation accounts for the many interactions between neighbors leading to improved accuracy.)
详见:Scalable Collaborative Filtering with Jointly Derived Neighborhood Interpolation Weights
1.3 隐语义模型(Latent factor models)
如果说前面的基于邻域的模型是统计方法,那么隐语义模型就是机器学习方法了,它有一个学习过程。例子很多,SVD,NMF,pLSA,以至于神经网络都可以算作隐语义模型。
对于基于SVD的隐语义模型具体介绍可见:从SVD到推荐系统。
这里说一点:对于推荐系统来说,评分矩阵是稀疏的。然而传统的SVD分解并没有告诉我们矩阵不完整的情况。对此,可以选择将稀疏的矩阵进行填充,使之变的dense后进行分解学习。但是,这无疑产生了很多无意义的数据和额外计算。而且,数据可能变得畸形。所以,对此,我们可以只选择有数据的评分进行分解,即:
\(min\sum_{(u,i)\in \mathcal{k}}(r_{ui}-\mu - b_i - b_u - \mathbf{q}_i^T\mathbf{p}_u)^2 + \lambda_{3} (\lVert p_u \rVert^2 + \lVert q_i \rVert^2 + b_u^2 + b_i^2)\tag{5}\)
以上为最小化损失函数,\(\mathcal{k}\)为用户u所有评分过的集合。
解决(5)式,一个简单的梯度下降就可以!👌
1.4 隐式反馈(Implicit feedback)
有两种用户偏好:
-
显式偏好(也称为“显式反馈”),比如用户对商品的“评分”
-
隐式偏好(也称为“隐式反馈”),比如“浏览”和“购买”历史记录
一个用户通过浏览或者某些历史记录来告诉我们他们对于某些物品的偏好。如用户在淘宝上购买了某个物品,即使该用户没有对此物品评分,但是这个购买记录也证明用户对这个物品有兴趣。所以,这里,我们新建一个二值矩阵,跟评分矩阵一样size。“1”代表有隐式偏好,“0”代表无隐式偏好。为了将这个东西一般化,我们定义两个集合:
- R(u): 用户u评分过的物品集合
- N(u): 用户u有过隐式偏好的物品集合
二、基于领域的模型
1.2节是基于邻域模型的一个basic,是一个基于统计的模型。本节介绍一种新的可进行全局优化方法的基于邻域的模型。这个模型有效的改善了准确度且结合了1.4节介绍的隐式偏好。
如1.2节,如(4)式,模型主要是求解插入权重\(\theta_{ij}^{u}\),为了更便于进行全局优化,我们使用了全局的权重\(\omega_{ij}\),而不在限定于某个用户。这个权重\(\omega_{ij}\)跟隐语义模型一样,是学习而来的,而不只是基于统计的量。一个简单的该模型的轮廓如下:
\(\hat r_{ui} = b_{ui}+\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}\tag{6}\)
这里的\(\omega_{ij}\)与(4) 式中的\(\theta_{ij}^{u}\)不同之处在于,前者跟user是没关系的,而后者有关系。
我们可以将\(\omega_{ij}\)看成baseline估计的一个抵消权重:\(r_{uj}-b_{uj}\)为实际值与baseline估计的残差,前面的系数即\(\omega_{ij}\)。对于两个很相似的物品i和j,\(\omega_{ij}\)会很大。那么,当用户u评分物品j时比估计得要高(即\(r_{uj}-b_{uj}\)大),那么我们可以在baseline的基础上增加\((r_{uj}-b_{uj})\omega_{ij}\)。相反的,如果用户评分j与baseline预测的一样(即即\(r_{uj}-b_{uj}\)接近0),那么\((r_{uj}-b_{uj})\omega_{ij}\)也接近于0,即物品j不对物品i的评分产生影响。(6)式其实可以总结为一句话:
我们加上1.4节提到的隐式偏好,用\(c_{ij}\)表示:
\(\hat r_{ui} = b_{ui}+\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}+\sum_{j\in N(u)}c_{ij}\tag{7}\)
跟\(\omega_{ij}\)一样\(c_{ij}\)也可以看作是加在baseline上的一个抵消(offset)。对于两个物品i和j,用户u对物品j隐式偏好可以通过\(c_{ij}\)影响\(\hat r_{ui}\)。
另外,一个用户opinion的组成不仅仅通过他评分的物品,也通过它没有评分的物品。例如,数据显示用户对《复仇者联盟3》评分高的人对《复仇者联盟1-2》也评分高。对此,评价了《复仇者联盟1-2》的人对评价《复仇者联盟3》有一个很高的权重。换句话说,如果一个用户没有评价过《复仇者联盟1-2》,那么对于该用户对《复仇者联盟3》的评价预测会有一个惩罚,分数会低一点。
在前面的模型(3),(4)中,都用到了\(b_{ui}\)这个值,即baseline的预测值。这里我们可以将\(b_{ui}\)用\(\widetilde b_{ui}\)代替。\(\widetilde b_{ui}\)为其他模型的预测(如SVD)。那么,我们可以将(7)式写成下面的形式:
\(\hat r_{ui} = \mu + b_{u}+b_{i}+\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}+\sum_{j\in N(U)}c_{ij}\tag{8}\)
\(b_{ui}\)是常值,仍然是baseline的预测。\(b_{u}\)和\(b_{i}\)是参数,这里通过学习得到。
至此为止,当前方法的一个特点为它对于评分多的用户(R(u)大)或者隐式偏好多的用户(N(u)大)有更大的偏离。即 \(\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}+\sum_{j\in N(U)}c_{ij}\) 越大。通常来说,这对推荐系统来说是一个好事。对于这些用户,我们可以提供更多冷门的推荐。另一方面,对于那些少操作的用户来说,我们只会给他们提供一些安全的大众的推荐。
然而,当前的模型(8)过分强调了重度使用用户和轻度用户的区别。所以,我们可以尝试做一个衰减,将(8)扩充为:
\(\hat r_{ui} = \mu + b_{u}+b_{i}+|R(u)|^{-\frac{1}{2}}\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}+|N(u)|^{-\frac{1}{2}}\sum_{j\in N(u)}c_{ij}\tag{9}\)
为了减小计算的复杂度,我们可以通过使用k items来减少一些参数。定义 \(S^{k}(i)\) 为物品i最相似的k个物品的集合。再定义\(R^{k}(i;u)=R(u)\cap S^{k}(i)\) 和 \(N^{k}(i;u)=N(u)\cap S^{k}(i)\)。
仍然,对i的评分影响最大的依然是与i相似度最大的k个物品,则:
\(\hat r_{ui} = \mu + b_{u}+b_{i}+|R^{k}(i;u)|^{-\frac{1}{2}}\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}+|N^{k}(i;u)|^{-\frac{1}{2}}\sum_{j\in N(u)}c_{ij}\tag{10}\)
当k取无穷大时,(10)与(9)等价。以上就是我们这节最终的模型,与1.2最大的不同就是它是一个全局优化的过程,而不是仅仅依赖与统计。所以,我们写出最小化损失函数:
\(min_{b*,\omega*,c*}\sum_{(u,i)\in k }(r_{ui}-\mu - b_{u}-b_{i}-|R^{k}(i;u)|^{-\frac{1}{2}}\sum_{j\in R(u)}(r_{uj}-b_{uj})\omega_{ij}-|N^{k}(i;u)|^{-\frac{1}{2}}\sum_{j\in N(U)}c_{ij})^2+\lambda_{4}(b_{u}^2+b_{i}^2+\sum_{j\in R^{k}(i;u)}\omega_{ij}^2+\sum_{j\in N^{k}(i;u)}c_{ij}^2)\tag{11}\)
我们定义预测误差为\(e_{ui}=r_{ui}-\hat r_{ui}\),利用梯度下降,我们的的参数更新循环为:
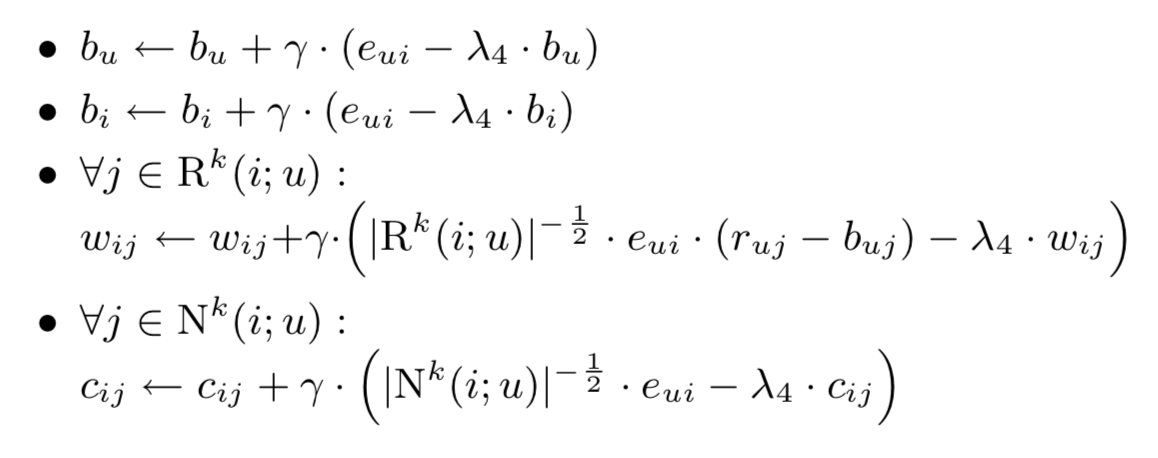
\(\gamma\)为学习率。
三、隐语义模型
我们这里介绍一个SVD-like的分解隐语义模型。首先,如1.3节介绍的SVD模型那样,我们可以把预测模型写成:
\(\hat r_{ui}=b_{ui}+p_{u}^Tq_{i}\tag{12}\)
这个预测函数对应的损失函数是公式(5)。现在,我们将这个模型引入隐式反馈已经我们在第二章介绍的东西,则式(12)可延伸为:
\(\hat r_{ui}=b_{ui}+ q_{i}^T( |R(u)|^{-\frac{1}{2}}\sum_{j\in R(u)}(r_{uj}-b_{uj})x_{j}+|N(u)|^{-\frac{1}{2}}\sum_{j\in N(u)}y_{j})\tag{13}\)
可以看到,每一个物品i与三个变量有联系:\(q_{i}, x_{i},y_{i}\in R^f\)。另一方面,我们没有直接用\(p_{u}\)这么显式的参数代表用户,而是通过用户喜欢的物品items来代表,即用\(|R(u)|^{-\frac{1}{2}}\sum_{j\in R(u)}(r_{uj}-b_{uj})x_{j}+|N(u)|^{-\frac{1}{2}}\sum_{j\in N(u)}y_{j}\)代替\(p_{u}\)。这个模型,我们叫做非对称SVD(Asymmetric-SVD)。以下介绍这个模型的几个优点:
- 更少的参数。 有人说(13)式明显比(12)式参数多,但是(12)式的\(p_{u}\)的行数为用户数,是一个巨大的量,而(13)式所有的参数都只跟物品数量有关。而在推荐系统中,用户数是远远大于物品数的。
- 新用户的冷启动。 因为Asymmetric-SVD没有参数化用户,只要新用户给予反馈该模型可以很快给出推荐,而不需要重新训练这个模型获取新参数。但是,如果一个新的物品引入进系统,那么这个模型需要一个waiting period来训练新的参数。
- 可解释性。 用户通常喜欢看到社区推荐物品的原因。这不仅提升了用户体验,同时增加了用户与社区的交互。事实上,标准的SVD模型无法很好提供解释,因为他是模型自己创造出来的特征。而Asymmetric-SVD的预测是直接通过用户的反馈来预测的。基于邻域的模型都有解释性好的优点。
- 隐式反馈的加入。 在(13)中,随着\(|N(u)|\)的增大,隐式反馈的影响也越大。另一方面,显式反馈也随着\(|R(u)|\)的增大而影响增大。
至此为止,我们可以写出(13)的最小化损失函数:
\(min_{q*,x*,y*,b*}\sum_{(u,i)\in k}(r_{ui}-b_{u}-b_{i}-q_{i}^T( |R(u)|^{-\frac{1}{2}}\sum_{j\in R(u)}(r_{uj}-b_{uj})x_{j}+|N(u)|^{-\frac{1}{2}}\sum_{j\in N(u)}y_{j}))^2+\lambda_{5} (\sum_{j\in R(u)}\lVert x_i+\sum_{j\in N(u)}\lVert y_i \rVert^2 + \lVert q_i \rVert^2 + b_u^2 + b_i^2)\tag{14}\)
上式在Netflix data的检验中的准确率比标准SVD有轻微的提高。这个改善应该感谢隐式反馈。
事实上,在SVD的基础上,如果只考虑隐式反馈的结合,更简单的写法,可以从(12)式直接加上隐式反馈量:
\(\hat r_{ui}=b_{ui}+ q_{i}^T(p_u+|N(u)|^{-\frac{1}{2}}\sum_{j\in N(u)}y_{j})\tag{15}\)
与(12)式不同的只在于对于用户user的表示。我们把(15)式的模型叫做SVD++(我写这篇博客的初衷)。
SVD++没有提供上述提到的优点的1,2,3,然而他已经足够的准确。
四、An Integrated Model
顾名思义,就是把两种方法结合。之前已经讨论过,隐语义模型和邻域模型的方法各有各的优点。在这一节,我们将邻域模型与SVD++模型进行结合。即:
这个公式相当于三个部分 的结合:
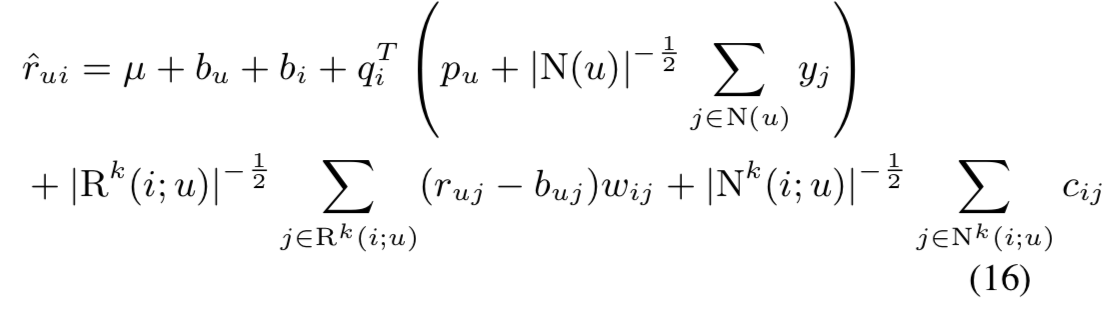
- \(\mu+b_u+b_i\)提供了user和item的基本属性,但并没有提供他们之间的interactions。
- \(q_{i}^T(p_u+|N(u)|^{-\frac{1}{2}}\sum_{j\in N(u)}y_{j})\)提供了user和item之间的interactions。
- 剩余部分式基于领域的部分,很难定义哈哈哈。
同样,我们的参数更新变成了以下过程:
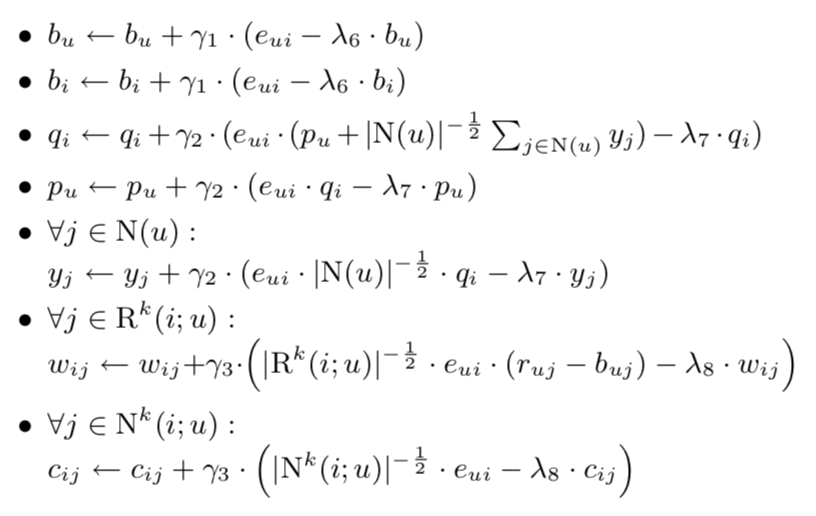



 浙公网安备 33010602011771号
浙公网安备 33010602011771号