Python数据结构应用5——排序(Sorting)

在具体算法之前,首先来看一下排序算法衡量的标准:
- 比较:比较两个数的大小的次数所花费的时间。
- 交换:当发现某个数不在适当的位置时,将其交换到合适位置花费的时间。
冒泡排序(Bubble Sort)
这是一个面试经常考的排序,虽然简单,但是要保证一点都不出错也不简单。
冒泡,顾名思义,每一次冒出一个泡泡出来,这个泡泡是剩余数中最大的那个数。所以,如果有n个数待排序,那么需要冒(n-1)次泡泡。即最外层循环需要len(list)-1次。
每一次冒泡的过程即内层循环。每次取一对数(pair),按顺序从最开始的一对数开始,比较两个数哪个数比较大就交换到上部(右边/冒泡),然后依次执行下一对数(每次进1),这个内层循环的次数随着外层循环的次数增加而减少,因为一旦进行了一次外层循环,已经排好序的数就多了一个。
一次冒泡的过程如下图:
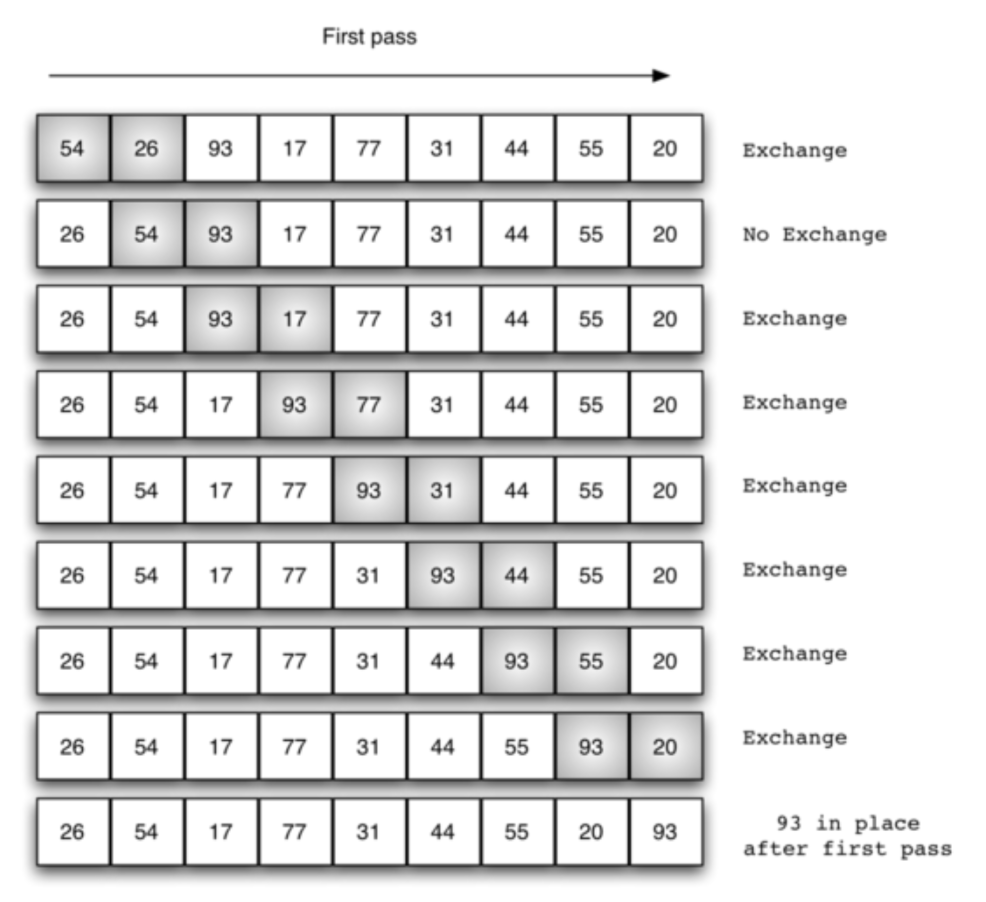
def bubble_sort(a_list):
for pass_num in range(len(a_list)-1,0,-1):
for i in range(pass_num):
if a_list[i] > a_list[i+1]:
a_list[i],a_list[i+1] = a_list[i+1],a_list[i]
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
bubble_sort(a_list)
print(a_list)
[17, 20, 26, 31, 44, 54, 55, 77, 93]
这种冒泡排序是很耗时间的,每一次外层循环,需要比较的次数如下图所示:

所以,一共需要\(\frac{1}{2}n^{2}-\frac{1}{2}n\) 次比较,时间复杂度是\(O(n^{2})\),如果看最坏的情况,即每次比较后都需要交换两个数,那么总时间✖️2
事实上,在很多情况下,冒泡排序并不需要完成所有的外循环就已经将所有数排好序啦,但是由于程序的笨蛋性,他还是在一直的执行下去,浪费时间。那么,我们可以将冒泡排序进行改进,让其知道一旦所有数据已经是按顺序排好时就停止工作,以进行时间优化:
def short_bubble_sort(a_list):
exchanges = True # 此标志用来记录一轮循环中是否进行了交换
pass_num = len(a_list)-1
while pass_num > 0 and exchanges:
exchanges = False
for i in range(pass_num):
if a_list[i]>a_list[i+1]:
exchanges = True
a_list[i],a_list[i+1] = a_list[i+1],a_list[i]
pass_num -= 1
a_list=[20, 30, 40, 90, 50, 60, 70, 80, 100, 110]
short_bubble_sort(a_list)
print(a_list)
[20, 30, 40, 50, 60, 70, 80, 90, 100, 110]
选择排序(Selection Sort)
选择排序其实每次外层循环的结果和冒泡排序很像,即每次在待排序元素中找到最大的元素,将其与应该放的位置交换。即每进行一次外层循环就多排好了一个元素。
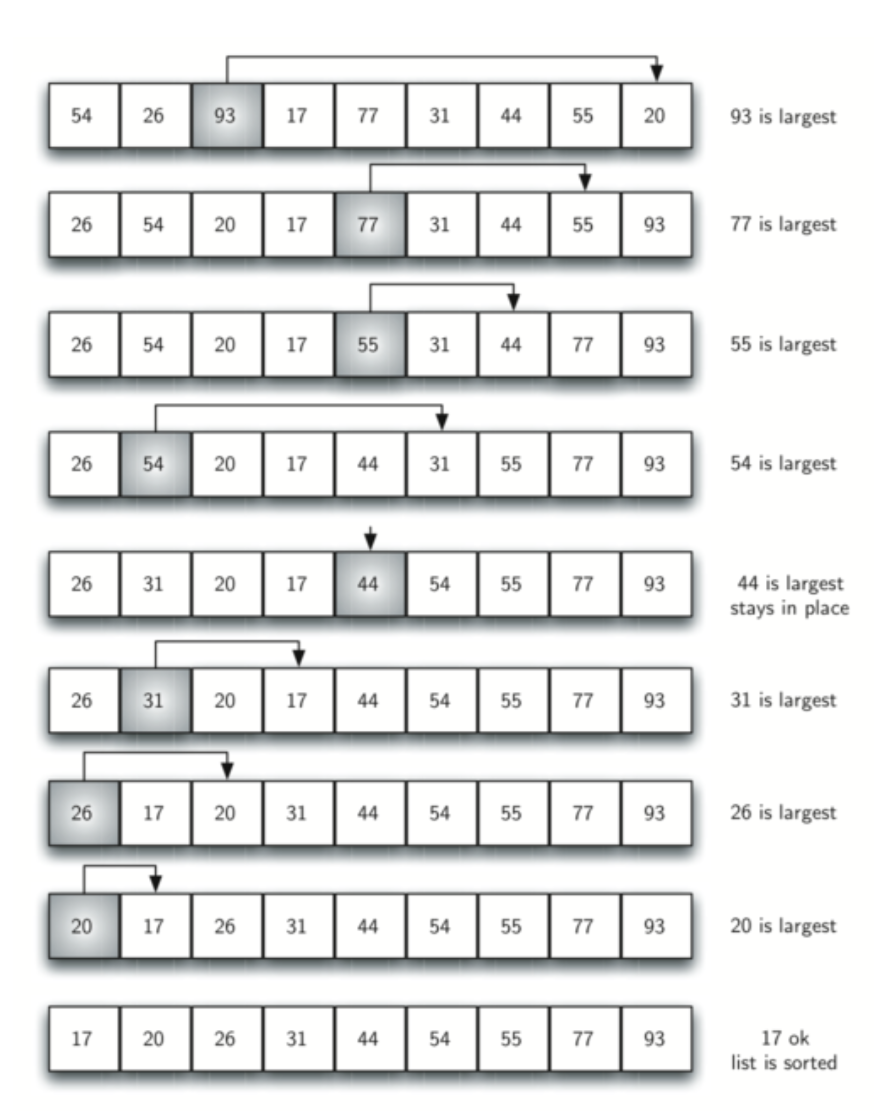
选择排序的时间复杂度仍为\(O(n^{2})\),但是由于其元素交换的次数比冒泡排序要少,所以消耗的时间比冒泡排序要短。
def selection_sort(a_list):
for fill_slot in range(len(a_list)-1,0,-1):
# fill_slot 这一轮最大元素将要放入的位置
pos_of_max=0
# 这一轮最大元素的位置
for location in range(1, fill_slot+1):
if a_list[location]>a_list[pos_of_max]:
pos_of_max = location
a_list[fill_slot],a_list[pos_of_max]=a_list[pos_of_max],a_list[fill_slot]
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
selection_sort(a_list)
print(a_list)
[17, 20, 26, 31, 44, 54, 55, 77, 93]
插入排序(Insertion Sort)
插入排序就像插扑克牌,每一次插一张牌到合适大小的位置,直到n张牌插入完毕。所以插入排序需要n-1次插入操作,即外层循环。每一次插入操作需要在已经排好序的数中依次进行比较,直到找到合适的位置。所以插入排序的时间复杂度在最好的情况下为\(O(n)\),最坏情况下为\(O(n^{2})\)。
插入排序过程如下图所示:

def insertion_sort(a_list):
for index in range(1, len(a_list)):
# index 为该轮要插入元素的位置
current_value = a_list[index]
position = index
while position>0 and a_list[position-1]>current_value:
a_list[position] = a_list[position-1]
position = position - 1
a_list[position] = current_value
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
insertion_sort(a_list)
print(a_list)
[17, 20, 26, 31, 44, 54, 55, 77, 93]
希尔排序(Shell Sort)
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率,但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
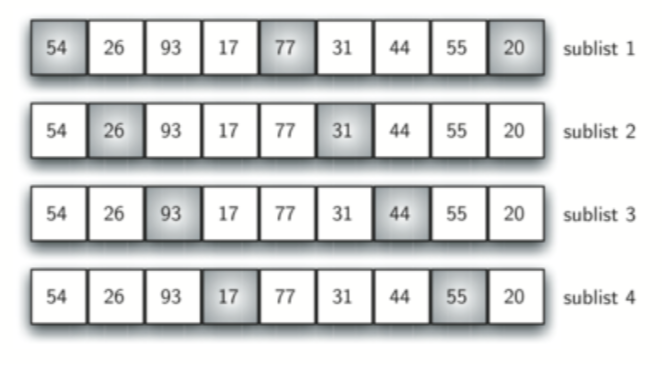
如下图所示,这个list中一共有9个数,我们将这9个数分成三个sublists,位置增量为3(如图每一列的深色部分为一个sublist)。对于每个sublist进行一次插入排序,且保持原来的位置放置在一个新的list中。
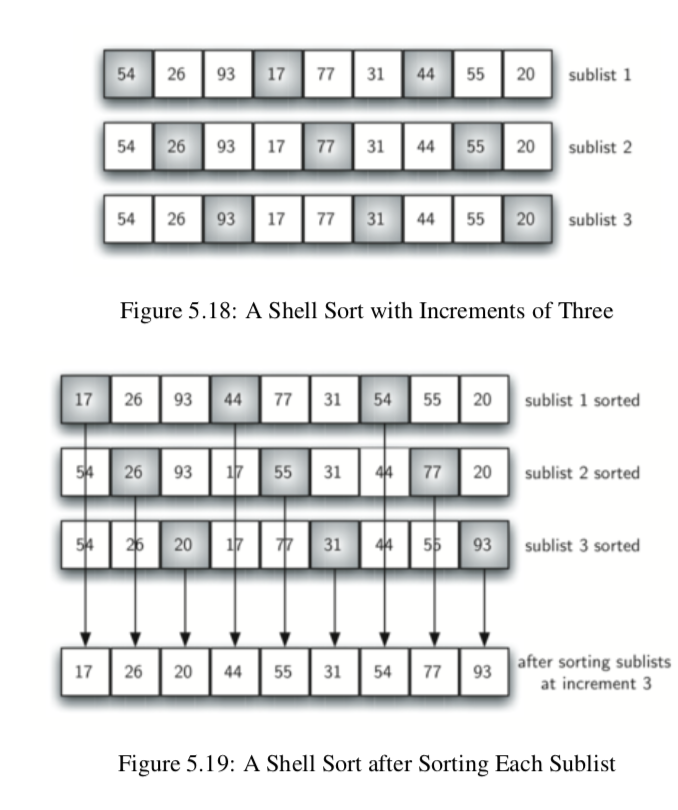
对于这个新的list,我们进行一次标准的插入排序。注意到,由于我们对于之前的sublist已经进行过排序,所以我们减少了这次标准插入排序的移动操作数。
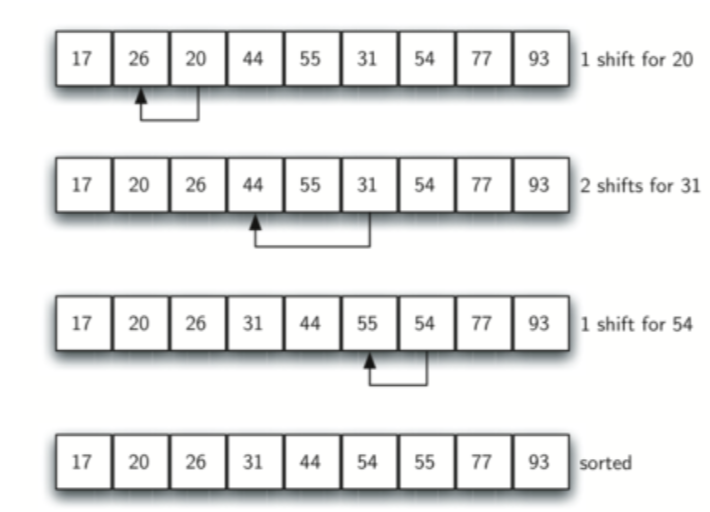
def shell_sort(a_list):
increment = len(a_list) // 2 # (步进数)
while increment > 0:
for start_position in range(increment):
gap_insertion_sort(a_list, start_position, increment)
print("After increments of size", increment, "The list is",a_list)
increment = increment // 2
def gap_insertion_sort(a_list, start, gap):
for i in range(start+gap, len(a_list), gap):
# 以下为插入排序
current_value = a_list[i]
position = i
while position >= gap and a_list[position-gap]>current_value:
a_list[position] = a_list[position-gap]
position = position - gap
a_list[position] = current_value
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
shell_sort(a_list)
print(a_list)
After increments of size 4 The list is [20, 26, 44, 17, 54, 31, 93, 55, 77]
After increments of size 2 The list is [20, 17, 44, 26, 54, 31, 77, 55, 93]
After increments of size 1 The list is [17, 20, 26, 31, 44, 54, 55, 77, 93]
[17, 20, 26, 31, 44, 54, 55, 77, 93]
步进increment在希尔排序中是一个重要的参数。上列函数shell_sort()使用了不同的步进。首先,创造了n/2个sublist,接下来,创造了n/4个sublist,步进也逐次减小。下图是第一次循环中的sublist选择:
归并排序(Merge Sort)
从这里,开始介绍分治策略(divide and conquer)。
归并排序其实跟二分搜索很相像,采用的是递归的方法。每次将待排序的list'平均'分成左右两个sublists,然后分别进行排序,依次递归,直到sublist的长度<=1。
第一个图是list的divide的过程:
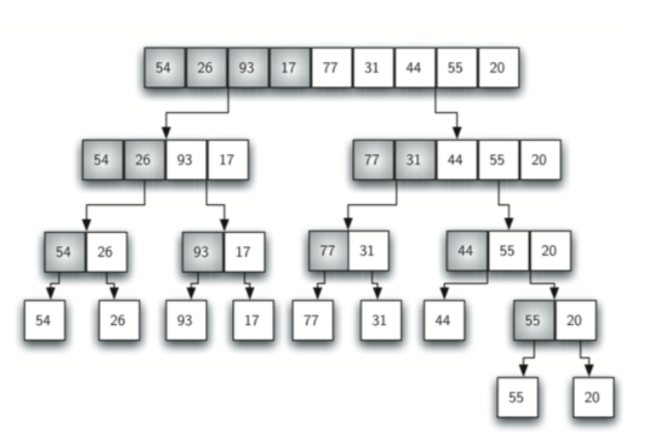
第二个图是sublists的conquer(merge)的过程:
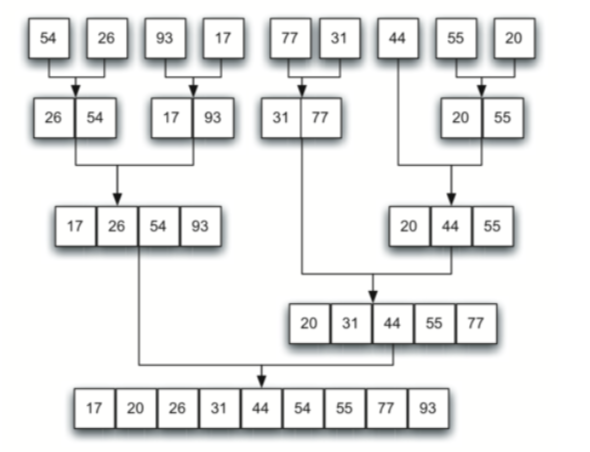
def merge_sort(a_list):
print('splitting', a_list)
if len(a_list)>1:
mid = len(a_list) // 2
# 这两个half需要额外的空间
left_half = a_list[:mid]
right_half = a_list[mid:]
merge_sort(left_half)
merge_sort(right_half)
# 当左右两个sublist都排好序时,每次选择两个sublist的最小的数
# 然后在这两数中选择更小的数依次放入待返回的list中
i,j,k=0,0,0
while i<len(left_half) and j<len(right_half):
if left_half[i] < right_half[j]:
a_list[k] = left_half[i]
i = i + 1
else:
a_list[k] = right_half[j]
j = j + 1
k = k + 1
while i < len(left_half):
a_list[k] = left_half[i]
i = i + 1
k = k + 1
while j < len(right_half):
a_list[k] = right_half[j]
j = j + 1
k = k + 1
print("Merging ", a_list)
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
merge_sort(a_list)
print(a_list)
splitting [54, 26, 93, 17, 77, 31, 44, 55, 20]
splitting [54, 26, 93, 17]
splitting [54, 26]
splitting [54]
splitting [26]
Merging [26, 54]
splitting [93, 17]
splitting [93]
splitting [17]
Merging [17, 93]
Merging [17, 26, 54, 93]
splitting [77, 31, 44, 55, 20]
splitting [77, 31]
splitting [77]
splitting [31]
Merging [31, 77]
splitting [44, 55, 20]
splitting [44]
splitting [55, 20]
splitting [55]
splitting [20]
Merging [20, 55]
Merging [20, 44, 55]
Merging [20, 31, 44, 55, 77]
Merging [17, 20, 26, 31, 44, 54, 55, 77, 93]
[17, 20, 26, 31, 44, 54, 55, 77, 93]
归并排序的时间复杂度,又是时候祭出这张图了(来自《算法导论》)。来看这个图,对于每一个conquer(merge)过程,merge后进行排序的时间消耗为len(sublist),在图中体现为n, n/2, n/4, ...。所以,图中每一行消耗的总时间为 n/len(sublist) * len(sublist),其中n为list的总长度。而一共有log(n)个这样的行,所以归并排序的时间复杂度为\(O(nlog(n))\)
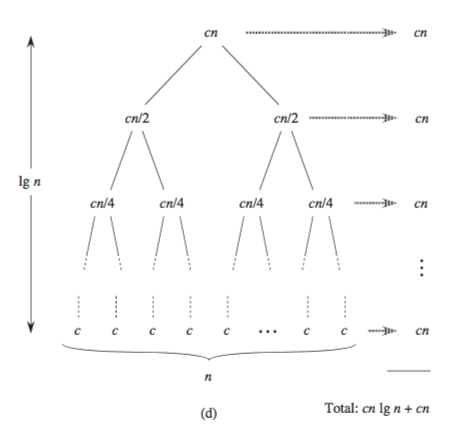
快速排序
快速排序也是一种分治策略,相对于归并排序来说,快速排序没有使用额外的空间。
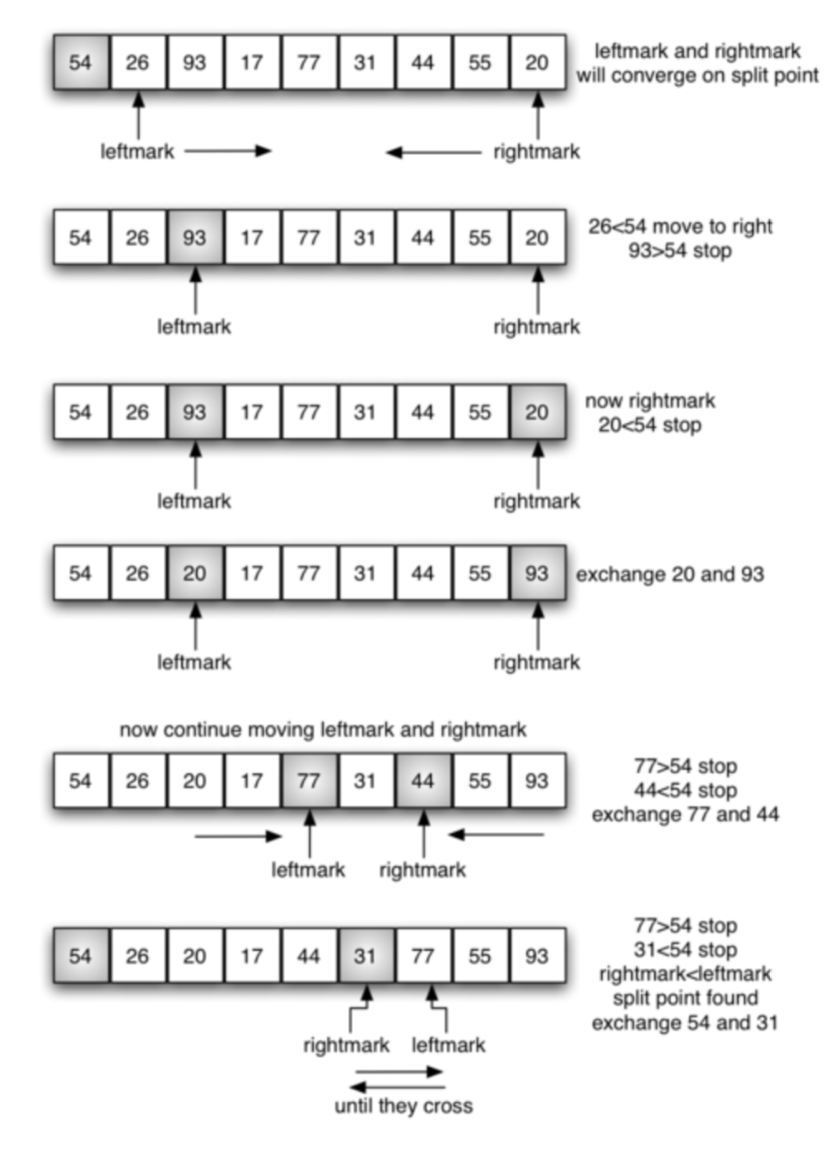
快速排序会在list中选择一个主元(pivot value),也可以叫它分割点(split point),通常是list的首尾元素,如下图,主元是54。接下来,在除去主元的剩余数中最左边为左标记(leftmark),最右边为右标记(rightmark),左标记向右移,直到移到的数小于主元数为止;右标记向左移,直到移到的数大于主元数为止。然后,交换此时两个标记的数。这个过程一直进行下去,直到两个标记移动交叉(cross)则停止移动。
此时,将主元数插入到左标记和右标记之间,则主元左边的数全都小于主元,主元右边的数全都大于主元。
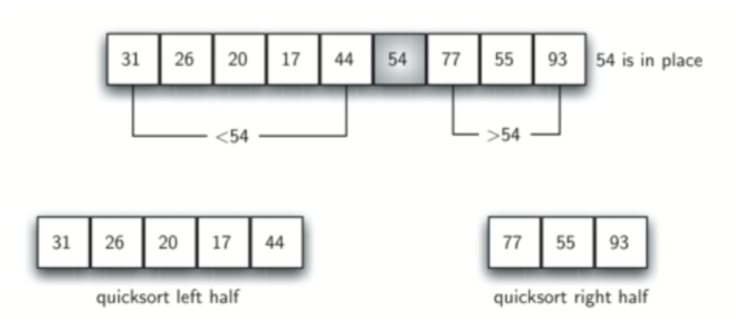
对左右两边的数构成的sublist进行递归quicksort。整个过程如下图:
def quick_sort(a_list):
quick_sort_helper(a_list, 0, len(a_list) - 1)
def quick_sort_helper(a_list, first, last):
# first和last分别是a_list的首尾位置,由于快速排序没有额外空间,
# 所以需要记录sublist的首尾位置
if first < last: # 若len(sublist)>0
split_point = partition(a_list, first, last)
quick_sort_helper(a_list, first, split_point - 1)
quick_sort_helper(a_list, split_point + 1, last)
def partition(a_list, first, last):
pivot_value = a_list[first]
left_mark = first+1
right_mark = last
done = False
while not done:
#
while left_mark <= right_mark and a_list[left_mark] <= pivot_value:
left_mark = left_mark + 1
while left_mark <= right_mark and a_list[right_mark] >= pivot_value:
right_mark = right_mark - 1
if right_mark < left_mark:
done = True
else: # (right_mark - left_mark) == 1
a_list[left_mark],a_list[right_mark]=a_list[right_mark],a_list[left_mark]
a_list[first],a_list[right_mark] = a_list[right_mark],a_list[first]
return right_mark
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
quick_sort(a_list)
print(a_list)
[17, 20, 26, 31, 44, 54, 55, 77, 93]
快速排序的时间复杂度取决于主元的选择,如果主元的大小每次都在整个list的中间,那么divide的过程则就类似于归并排序的过程,时间复杂度的结果就是\(O(nlog(n))\)。
然而,并不是所有情况都是这么好的。想象一下最坏情况,如果每次主元都正好选到了剩余list中最小或者最大的那个数,则每次divide只能分割掉一个元素,这就和选择排序基本无异了,时间复杂度上升为\(O(n^{2})\)
所以,为了避免这种情况的发生,我们可以尝试随机选择主元,这可以减少原始数据的本来结构对于复杂度的影响。
- Reference:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号