nchu-software-oop-2022第4~5次作业分析暨期中考试总结
一、前言
这几周完成的PTA第4~6次大作业(第6次作业下次博客见)以及期中考试的题目基本围绕同一主题:点线形展开。从之前的三角形,到这次的四边形、五边形,题目难度依次递增,题面逐渐变得狰狞。题目虽然变得更复杂了,对于类、继承、抽象等面向对象的思想及设计的要求也更高了,但是只要足够耐心和细心,依然可以很快完成。我这次的作业代码在第三次的基础上,做了一些优化,比如终于开始用类了习惯不好。经过点线型系列作业前几题的训练摧残后,我在写这次作业时,思路、实现过程比上次要清晰许多,在题目难度更大的情况下用更短的时间完成了作业。本篇博客将对PTA第4~5次作业以及期中考试的题目以及代码进行逐一分析。好,话不多说,直接开整!
二、设计分析
第四次大作业T1
题面:
背景简介:
“蛟龙号”载人深潜器是我国首台自主设计、自主集成研制的作业型深海载人潜水器,设计最大下潜深度为7000米级,也是目前世界上下潜能力最强的作业型载人潜水器。“蛟龙号”可在占世界海洋面积99.8%的广阔海域中使用,对于我国开发利用深海的资源有着重要的意义。
中国是继美、法、俄、日之后世界上第五个掌握大深度载人深潜技术的国家。在全球载人潜水器中,“蛟龙号”属于第一梯队。目前全世界投入使用的各类载人潜水器约90艘,其中下潜深度超过1000米的仅有12艘,更深的潜水器数量更少,目前拥有6000米以上深度载人潜水器的国家包括中国、美国、日本、法国和俄罗斯。除中国外,其他4国的作业型载人潜水器最大工作深度为日本深潜器的6527米,因此“蛟龙号”载人潜水器在西太平洋的马里亚纳海沟海试成功到达7020米海底,创造了作业类载人潜水器新的世界纪录。
从2009年至2012年,蛟龙号接连取得1000米级、3000米级、5000米级和7000米级海试成功。下潜至7000米,说明蛟龙号载人潜水器集成技术的成熟,标志着我国深海潜水器成为海洋科学考察的前沿与制高点之一。
2012年6月27日11时47分,中国“蛟龙”再次刷新“中国深度”——下潜7062米。6月3日,“蛟龙”出征以来,已经连续书写了5个“中国深度”新纪录:6月15日,6671米;6月19日,6965米;6月22日,6963米;6月24日,7020米;6月27日,7062米。下潜至7000米,标志着我国具备了载人到达全球99%以上海洋深处进行作业的能力,标志着“蛟龙”载人潜水器集成技术的成熟,标志着我国深海潜水器成为海洋科学考察的前沿与制高点之一,标志着中国海底载人科学研究和资源勘探能力达到国际领先水平。
‘蛟龙’号是我国载人深潜发展历程中的一个重要里程碑。它不只是一个深海装备,更代表了一种精神,一种不畏艰险、赶超世界的精神,它是中华民族进军深海的号角。
了解蛟龙号”载人深潜器“的骄人业绩,为我国海底载人科学研究和资源勘探能力达到国际领先水平而自豪,小伙伴们与祖国同呼吸、共命运,一定要学好科学文化知识、提高个人能力,增强创新意识,做事精益求精,立科技报国之志!
请编写程序,实现如下功能:读入关于蛟龙号载人潜水器探测数据的多行字符串,从给定的信息找出数字字符,输出每行的数字之和。
提示 若输入为“2012年2月”,则该行的输出为:2014。若干个连续的数字字符作为一个整体,以十进制形式相加。
输入格式:
读入关于蛟龙号载人潜水器探测数据的多行字符串,每行字符不超过80个字符。
以"end"结束。
输出格式:
与输入行相对应的各个整数之和。
输入样例1:
2012年6月27日11时47分,中国“蛟龙”再次刷新“中国深度”——下潜7062米
6月15日,6671米
6月19日,6965米
6月22日,6963米
6月24日,7020米
6月27日,7062米
下潜至7000米,标志着我国具备了载人到达全球99%以上海洋深处进行作业的能力
end输出样例1:
9165
6692
6990
6991
7050
7095
7099
题面非常长啊,但题目只考察了一个知识点——用正则表达式从字符串中提取数字。直接上代码:
import java.util.*; import java.text.DecimalFormat; import java.io.*; import java.lang.*; import java.math.*; import java.net.*; import java.text.*; import java.text.NumberFormat; public class Main{ public static void main(String[] args){ Scanner bjsn=new Scanner(System.in); String s=null; while(!(s=bjsn.nextLine()).equals("end")){//判断是否输入结束 String[] t=s.split("\\D+");//正整数提取 int cnt=0; for(String str:t){ if(!str.equals("")){ cnt+=Integer.parseInt(str); } } System.out.println(cnt); } } }
此题过于简单,就不做sourcemonitor的分析啦!不过,不仅仅是深潜,成为科技强国,责任在于吾辈!
第四次大作业T2
题面:
用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y
5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
选项1、2、3中,若四边形四个点中有重合点,输出"points coincide"。
选项4中,若前两个输入线的点重合,输出"points coincide"。
输入样例1:
选项1,点重合。例如:
1:-1,-1 -1,-1 1,2 1,-2
输出样例:
在这里给出相应的输出。例如:
points coincide
一看就知道,第四次大作业的重头戏来啦!代码非常不规范啊。下面讲讲case4我的思路并不规范。
找出离分割线左右两边最远的点,设为1和4
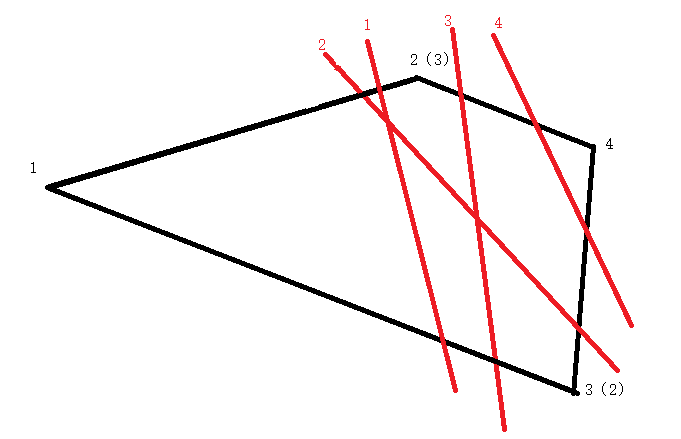
大概就是上面这几种情况吧。。然后分割一下求面积就好了。
我那新鲜又美味的代码:
import java.util.*; import java.text.DecimalFormat; import java.io.*; import java.lang.*; import java.math.*; import java.net.*; import java.text.*; import java.text.NumberFormat; public class Main{ static double P1=0,P2=0,Q1=0,Q2=0,R1=0,R2=0,T1=0,T2=0,S1=0,S2=0,W1=0,W2=0; public static void main(String[] args) { Scanner bjsn = new Scanner(System.in); String s = bjsn.nextLine(); int len = s.length(); //格式判断 if (s.charAt(0) < '1' || s.charAt(0) > '5' || s.charAt(1) != ':') { System.out.println("Wrong Format"); return; } int cnt = 0; for (int i = 0; i < len; i++) { if (s.charAt(i) == ',') { cnt++; } } if (cnt == 0) { System.out.println("Wrong Format"); return; } int pos = 2; if ((s.charAt(pos) != '+' && s.charAt(pos) != '-') && (s.charAt(pos) < '0' || s.charAt(pos) > '9')) { System.out.println("Wrong Format"); return; } String sss = s.substring(2, len); String ss[] = sss.split(" "); String str[] = null; for (String Str : ss) { str = Str.split(","); for (String tt : str) { if (!tt.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")) { System.out.println("Wrong Format"); return; } } } switch (s.charAt(0)) { case '1': if (ss.length != 4) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; }//提取点 str = ss[0].split(","); P1 = Double.parseDouble(str[0]); P2 = Double.parseDouble(str[1]); str = ss[1].split(","); Q1 = Double.parseDouble(str[0]); Q2 = Double.parseDouble(str[1]); str = ss[2].split(","); R1 = Double.parseDouble(str[0]); R2 = Double.parseDouble(str[1]); str = ss[3].split(","); T1 = Double.parseDouble(str[0]); T2 = Double.parseDouble(str[1]); if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { System.out.println("points coincide"); return; } if ((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) || (Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) || (R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) || (T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2)) { System.out.println("false false"); return; } if (!check2(P1, P2, Q1, Q2, R1, R2, T1, T2)) { System.out.println("false false"); return; } if ((P2 - Q2) * (R1 - T1) == (P1 - Q1) * (R2 - T2) && (P2 - T2) * (Q1 - R1) == (P1 - T1) * (Q2 - R2)) { System.out.println("true true"); } else { System.out.println("true false"); } break; case '2': if (ss.length != 4) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str = ss[0].split(","); P1 = Double.parseDouble(str[0]); P2 = Double.parseDouble(str[1]); str = ss[1].split(","); Q1 = Double.parseDouble(str[0]); Q2 = Double.parseDouble(str[1]); str = ss[2].split(","); R1 = Double.parseDouble(str[0]); R2 = Double.parseDouble(str[1]); str = ss[3].split(","); T1 = Double.parseDouble(str[0]); T2 = Double.parseDouble(str[1]); if ((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) || (Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) || (R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) || (T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2)) { System.out.println("not a quadrilateral"); return; } if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { System.out.println("points coincide"); return; } if (!check2(P1, P2, Q1, Q2, R1, R2, T1, T2)) { System.out.println("not a quadrilateral"); return; } double PQf = (P1 - Q1) * (P1 - Q1) + (P2 - Q2) * (P2 - Q2); double PTf = (P1 - T1) * (P1 - T1) + (P2 - T2) * (P2 - T2); double QRf = (Q1 - R1) * (Q1 - R1) + (Q2 - R2) * (Q2 - R2); double RTf = (R1 - T1) * (R1 - T1) + (R2 - T2) * (R2 - T2); if (PQf == QRf && PQf == RTf && PTf == RTf) { if ((P2 - Q2) * (Q2 - R2) == -(P1 - Q1) * (Q1 - R1) || (P1 == Q1 && Q2 == R2) || (Q1 == R1 && P2 == R2)) { System.out.println("true true true"); } else { System.out.println("true false false"); } } else if (((P2 - Q2) * (Q2 - R2) == -(P1 - Q1) * (Q1 - R1) && (R2 - T2) * (Q2 - R2) == -(Q1 - R1) * (R1 - T1) && (R2 - T2) * (T2 - P2) == -(R1 - T1) * (T1 - P1)) || ((P1 == Q1 && Q2 == R2) && (R1 == T1 && T2 == P2)) || ((P1 == T1 && P2 == Q2) && (Q1 == R1 && R2 == T2))) { System.out.println("false true false"); } else { System.out.println("false false false"); } break; case '3': if (ss.length != 4) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str = ss[0].split(","); P1 = Double.parseDouble(str[0]); P2 = Double.parseDouble(str[1]); str = ss[1].split(","); Q1 = Double.parseDouble(str[0]); Q2 = Double.parseDouble(str[1]); str = ss[2].split(","); R1 = Double.parseDouble(str[0]); R2 = Double.parseDouble(str[1]); str = ss[3].split(","); T1 = Double.parseDouble(str[0]); T2 = Double.parseDouble(str[1]); if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { System.out.println("points coincide"); return; } if ((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) || (Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) || (R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) || (T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2)) { System.out.println("not a quadrilateral"); return; } boolean flag = true; boolean f1 = check(P1, P2, Q1, Q2, R1, R2, T1, T2); boolean f2 = check(Q1, Q2, P1, P2, R1, R2, T1, T2); boolean f3 = check(R1, R2, P1, P2, Q1, Q2, T1, T2); boolean f4 = check(T1, T2, P1, P2, Q1, Q2, R1, R2); if (f1 || f2 || f3 || f4) { flag = false; } double PQ = Math.sqrt((P1 - Q1) * (P1 - Q1) + (P2 - Q2) * (P2 - Q2)); double PR = Math.sqrt((P1 - R1) * (P1 - R1) + (P2 - R2) * (P2 - R2)); double PT = Math.sqrt((P1 - T1) * (P1 - T1) + (P2 - T2) * (P2 - T2)); double QR = Math.sqrt((Q1 - R1) * (Q1 - R1) + (Q2 - R2) * (Q2 - R2)); double RT = Math.sqrt((R1 - T1) * (R1 - T1) + (R2 - T2) * (R2 - T2)); double QT = Math.sqrt((Q1 - T1) * (Q1 - T1) + (Q2 - T2) * (Q2 - T2)); double C = PQ + QR + RT + PT; double p1 = (PQ + QR + PR) / 2; double s1 = Math.sqrt(p1 * (p1 - PQ) * (p1 - QR) * (p1 - PR)); double p2 = (PR + PT + RT) / 2; double s2 = Math.sqrt(p2 * (p2 - PR) * (p2 - PT) * (p2 - RT)); if (f2 || f4) { p1 = (PQ + PT + QT) / 2; s1 = Math.sqrt(p1 * (p1 - PQ) * (p1 - PT) * (p1 - QT)); p2 = (QR + QT + RT) / 2; s2 = Math.sqrt(p2 * (p2 - QR) * (p2 - QT) * (p2 - RT)); } BigDecimal Cc = new BigDecimal(C); C = Cc.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); BigDecimal Ss = new BigDecimal(s1 + s2); double S = Ss.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); if (flag) { System.out.println("true " + C + " " + S); } else { System.out.println("false " + C + " " + S); } break; case '4': if (ss.length != 6) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str = ss[0].split(","); S1 = Double.parseDouble(str[0]); S2 = Double.parseDouble(str[1]); str = ss[1].split(","); W1 = Double.parseDouble(str[0]); W2 = Double.parseDouble(str[1]); str = ss[2].split(","); P1 = Double.parseDouble(str[0]); P2 = Double.parseDouble(str[1]); str = ss[3].split(","); Q1 = Double.parseDouble(str[0]); Q2 = Double.parseDouble(str[1]); str = ss[4].split(","); R1 = Double.parseDouble(str[0]); R2 = Double.parseDouble(str[1]); str = ss[5].split(","); T1 = Double.parseDouble(str[0]); T2 = Double.parseDouble(str[1]); int ans=0; if ((S1 - W1 == 0 && S2 - W2 == 0)) { System.out.println("points coincide"); return; } if (!check2(P1, P2, Q1, Q2, R1, R2, T1, T2)) { System.out.println("not a quadrilateral or triangle"); return; } if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { if(P1 - Q1 == 0 && P2 - Q2 == 0)ans++; if(P1 - R1 == 0 && P2 - R2 == 0)ans++; if(P1 - T1 == 0 && P2 - T2 == 0)ans++; if(Q1 - R1 == 0 && Q2 - R2 == 0)ans++; if(Q1 - T1 == 0 && Q2 - T2 == 0)ans++; if(R1 - T1 == 0 && R2 - T2 == 0)ans++; if(ans>1){ System.out.println("not a quadrilateral or triangle"); return; } } if (((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) && ((Q1 > Math.max(P1, R1) || Q1 < Math.min(P1, R1)) || (Q2 > Math.max(P2, R2) || Q2 < Math.min(P2, R2)))) || ((Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) && ((R1 > Math.max(Q1, T1) || R1 < Math.min(Q1, T1)) || (R2 > Math.max(Q2, T2) || R2 < Math.min(Q2, T2)))) || ((R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) && ((T1 > Math.max(P1, R1) || T1 < Math.min(P1, R1)) || (T2 > Math.max(P2, R2) || T2 < Math.min(P2, R2)))) || ((T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2) && ((P1 > Math.max(T1, Q1) || P1 < Math.min(T1, Q1)) || (P2 > Math.max(T2, Q2) || P2 < Math.min(T2, Q2))))) { if(ans==0){ System.out.println("not a quadrilateral or triangle"); return; } } int bpx=0; if((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2))bpx++; if((Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2))bpx++; if((R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2))bpx++; if((T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2))bpx++; if((bpx>1&&ans==0)||(bpx>3&&ans>0)){ System.out.println("not a quadrilateral or triangle"); return; } double ss0 = 0; if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { if (P1 - Q1 == 0 && P2 - Q2 == 0) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, R1, R2, T1, T2); } else if (Q1 - R1 == 0 && Q2 - R2 == 0) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, R1, R2, T1, T2); } else if ((R1 - T1 == 0 && R2 - T2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0)) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, Q1, Q2, T1, T2); } else if ((T1 - P1 == 0 && T2 - P2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0)) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, Q1, Q2, R1, R2); } } else if ((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) || (Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) || (R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) || (T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2)) { if ((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2)) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, R1, R2, T1, T2); } else if ((Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2)) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, Q1, Q2, T1, T2); } else if ((R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2)) { ss0 = Scalc_3(S1, S2, W1, W2, P1, P2, Q1, Q2, R1, R2); } else { ss0 = Scalc_3(S1, S2, W1, W2, T1, T2, Q1, Q2, R1, R2); } } else { double At = W2 - S2, Bt = S1 - W1, Ct = W1 * S2 - W2 * S1; double Dis[] = new double[4]; double X[] = new double[4]; double Y[] = new double[4]; X[0] = P1; X[1] = Q1; X[2] = R1; X[3] = T1; Y[0] = P2; Y[1] = Q2; Y[2] = R2; Y[3] = T2; Dis[0] = dis(At, Bt, Ct, P1, P2); Dis[1] = dis(At, Bt, Ct, Q1, Q2); Dis[2] = dis(At, Bt, Ct, R1, R2); Dis[3] = dis(At, Bt, Ct, T1, T2); double min1 = Dis[0]; int loc1 = 0; for (int i = 0; i < 4; i++) { if (min1 > Dis[i]) { min1 = Dis[i]; loc1 = i; } } double min2 = Dis[0]; int loc2 = 0; if (loc1 == 0) { min2 = Dis[1]; loc2 = 1; } for (int i = 0; i < 4; i++) { if (min2 > Dis[i] && i != loc1) { min2 = Dis[i]; loc2 = i; } } double max1 = Dis[0]; int loc4 = 0; for (int i = 0; i < 4; i++) { if (max1 < Dis[i]) { max1 = Dis[i]; loc4 = i; } } int loc3 = 0; for (int i = 0; i < 4; i++) { if (i != loc1 && i != loc2 && i != loc4) { loc3 = i; } } if ((S2 - W2) * (X[loc4] - X[loc3]) == (S1 - W1) * (Y[loc4] - Y[loc3])) { double res = Scalc_4(S1, S2, W1, W2, X[loc2], Y[loc2], X[loc1], Y[loc1], X[loc4], Y[loc4], X[loc3], Y[loc3]); } else { f1 = check(X[loc1], Y[loc1], X[loc2], Y[loc2], X[loc3], Y[loc3], X[loc4], Y[loc4]); f2 = check(X[loc2], Y[loc2], X[loc1], Y[loc1], X[loc3], Y[loc3], X[loc4], Y[loc4]); f3 = check(X[loc3], Y[loc3], X[loc1], Y[loc1], X[loc2], Y[loc2], X[loc4], Y[loc4]); f4 = check(X[loc4], Y[loc4], X[loc1], Y[loc1], X[loc2], Y[loc2], X[loc3], Y[loc3]); if (!f1 && !f2 && !f3 && !f4) { if((S2-W2)*(X[loc1]-X[loc2])==(Y[loc1]-Y[loc2])*(S1-W1)) { double res = Scalc_4(S1, S2, W1, W2, X[loc1], Y[loc1], X[loc2], Y[loc2], X[loc3], Y[loc3], X[loc4], Y[loc4]); } else{ double res = Scalc_4(S1, S2, W1, W2, X[loc2], Y[loc2], X[loc1], Y[loc1], X[loc3], Y[loc3], X[loc4], Y[loc4]); } } else { f1 = check(P1, P2, Q1, Q2, R1, R2, T1, T2); f2 = check(Q1, Q2, P1, P2, R1, R2, T1, T2); f3 = check(R1, R2, P1, P2, Q1, Q2, T1, T2); f4 = check(T1, T2, P1, P2, Q1, Q2, R1, R2); if (f1) { double res = Scalc_4o(S1, S2, W1, W2, T1, T2, P1, P2, Q1, Q2, R1, R2); } else if (f2) { double res = Scalc_4o(S1, S2, W1, W2, P1, P2, Q1, Q2, R1, R2, T1, T2); } else if (f3) { double res = Scalc_4o(S1, S2, W1, W2, Q1, Q2, R1, R2, T1, T2, P1, P2); } else if (f4) { double res = Scalc_4o(S1, S2, W1, W2, R1, R2, T1, T2, P1, P2, Q1, Q2); } } } } break; case '5': if (ss.length != 5) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str = ss[0].split(","); S1 = Double.parseDouble(str[0]); S2 = Double.parseDouble(str[1]); str = ss[1].split(","); P1 = Double.parseDouble(str[0]); P2 = Double.parseDouble(str[1]); str = ss[2].split(","); Q1 = Double.parseDouble(str[0]); Q2 = Double.parseDouble(str[1]); str = ss[3].split(","); R1 = Double.parseDouble(str[0]); R2 = Double.parseDouble(str[1]); str = ss[4].split(","); T1 = Double.parseDouble(str[0]); T2 = Double.parseDouble(str[1]); ans=0; if (!check2(P1, P2, Q1, Q2, R1, R2, T1, T2)) { System.out.println("not a quadrilateral or triangle"); return; } if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { if(P1 - Q1 == 0 && P2 - Q2 == 0)ans++; if(P1 - R1 == 0 && P2 - R2 == 0)ans++; if(P1 - T1 == 0 && P2 - T2 == 0)ans++; if(Q1 - R1 == 0 && Q2 - R2 == 0)ans++; if(Q1 - T1 == 0 && Q2 - T2 == 0)ans++; if(R1 - T1 == 0 && R2 - T2 == 0)ans++; if(ans>1){ System.out.println("not a quadrilateral or triangle"); return; } } bpx=0; if((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2))bpx++; if((Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2))bpx++; if((R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2))bpx++; if((T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2))bpx++; if((bpx>1&&ans==0)||(bpx>3&&ans>0)){ System.out.println("not a quadrilateral or triangle"); return; } if (((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) && ((Q1 > Math.max(P1, R1) || Q1 < Math.min(P1, R1)) || (Q2 > Math.max(P2, R2) || Q2 < Math.min(P2, R2)))) || ((Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) && ((R1 > Math.max(Q1, T1) || R1 < Math.min(Q1, T1)) || (R2 > Math.max(Q2, T2) || R2 < Math.min(Q2, T2)))) || ((R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) && ((T1 > Math.max(P1, R1) || T1 < Math.min(P1, R1)) || (T2 > Math.max(P2, R2) || T2 < Math.min(P2, R2)))) || ((T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2) && ((P1 > Math.max(T1, Q1) || P1 < Math.min(T1, Q1)) || (P2 > Math.max(T2, Q2) || P2 < Math.min(T2, Q2))))) { if(ans==0){ System.out.println("not a quadrilateral or triangle"); return; } } boolean isTriangle = false; if ((P1 - Q1 == 0 && P2 - Q2 == 0) || (P1 - R1 == 0 && P2 - R2 == 0) || (P1 - T1 == 0 && P2 - T2 == 0) || (Q1 - R1 == 0 && Q2 - R2 == 0) || (Q1 - T1 == 0 && Q2 - T2 == 0) || (R1 - T1 == 0 && R2 - T2 == 0)) { isTriangle = true; } else if ((P2 - Q2) * (Q1 - R1) == (P1 - Q1) * (Q2 - R2) || (Q2 - R2) * (R1 - T1) == (Q1 - R1) * (R2 - T2) || (R2 - T2) * (T1 - P1) == (R1 - T1) * (T2 - P2) || (T2 - P2) * (Q1 - P1) == (T1 - P1) * (Q2 - P2)) { isTriangle = true; } PQ = Math.sqrt((P1 - Q1) * (P1 - Q1) + (P2 - Q2) * (P2 - Q2)); PT = Math.sqrt((P1 - T1) * (P1 - T1) + (P2 - T2) * (P2 - T2)); QR = Math.sqrt((Q1 - R1) * (Q1 - R1) + (Q2 - R2) * (Q2 - R2)); RT = Math.sqrt((R1 - T1) * (R1 - T1) + (R2 - T2) * (R2 - T2)); PR = Math.sqrt((P1 - R1) * (P1 - R1) + (P2 - R2) * (P2 - R2)); QT = Math.sqrt((Q1 - T1) * (Q1 - T1) + (Q2 - T2) * (Q2 - T2)); double PS = Math.sqrt((P1 - S1) * (P1 - S1) + (P2 - S2) * (P2 - S2)); double QS = Math.sqrt((Q1 - S1) * (Q1 - S1) + (Q2 - S2) * (Q2 - S2)); double RS = Math.sqrt((R1 - S1) * (R1 - S1) + (R2 - S2) * (R2 - S2)); double TS = Math.sqrt((T1 - S1) * (T1 - S1) + (T2 - S2) * (T2 - S2)); double p_1 = (PT + PS + TS) / 2; double p_2 = (PS + PQ + QS) / 2; double p_3 = (QS + QR + RS) / 2; double p_4 = (RS + TS + RT) / 2; double Spts = Math.sqrt(p_1 * (p_1 - PT) * (p_1 - PS) * (p_1 - TS)); double Spqs = Math.sqrt(p_2 * (p_2 - PS) * (p_2 - PQ) * (p_2 - QS)); double Sqrs = Math.sqrt(p_3 * (p_3 - QS) * (p_3 - QR) * (p_3 - RS)); double Srts = Math.sqrt(p_4 * (p_4 - RS) * (p_4 - TS) * (p_4 - RT)); double tS = Spts + Spqs + Sqrs + Srts; f2 = check(Q1, Q2, P1, P2, R1, R2, T1, T2); f4 = check(T1, T2, P1, P2, Q1, Q2, R1, R2); p1 = (PQ + QR + PR) / 2; s1 = Math.sqrt(p1 * (p1 - PQ) * (p1 - QR) * (p1 - PR)); p2 = (PR + PT + RT) / 2; s2 = Math.sqrt(p2 * (p2 - PR) * (p2 - PT) * (p2 - RT)); if (f2 || f4) { p1 = (PQ + PT + QT) / 2; s1 = Math.sqrt(p1 * (p1 - PQ) * (p1 - PT) * (p1 - QT)); p2 = (QR + QT + RT) / 2; s2 = Math.sqrt(p2 * (p2 - QR) * (p2 - QT) * (p2 - RT)); } double S_0 = s1 + s2; if (Math.abs(S_0 - tS) < 0.0000001) { if (Spts > 0 && Spqs > 0 && Sqrs > 0 && Srts > 0) { if (isTriangle) { System.out.println("in the triangle"); } else { System.out.println("in the quadrilateral"); } } else { if (isTriangle) { int Cnt=0; if(Math.abs(Spts)<0.0000001)Cnt++; if(Math.abs(Spqs)<0.0000001)Cnt++; if(Math.abs(Sqrs)<0.0000001)Cnt++; if(Math.abs(Srts)<0.0000001)Cnt++; if(Cnt==1)System.out.println("in the triangle"); else System.out.println("on the triangle"); } else { System.out.println("on the quadrilateral"); } } } else { if (isTriangle) { System.out.println("outof the triangle"); } else { System.out.println("outof the quadrilateral"); } } break; } } static boolean check(double P1,double P2,double Q1,double Q2,double R1,double R2,double T1,double T2) {//点是否在三角形内 double a = Math.sqrt((T1 - R1) * (T1 - R1) + (T2 - R2) * (T2 - R2)); double b = Math.sqrt((T1 - Q1) * (T1 - Q1) + (T2 - Q2) * (T2 - Q2)); double c = Math.sqrt((R1 - Q1) * (R1 - Q1) + (R2 - Q2) * (R2 - Q2)); double p = (a + b + c) / 2; double S = Math.sqrt(p * (p - a) * (p - b) * (p - c)); double Pq = Math.sqrt((P1 - Q1) * (P1 - Q1) + (P2 - Q2) * (P2 - Q2)); double Pr = Math.sqrt((P1 - R1) * (P1 - R1) + (P2 - R2) * (P2 - R2)); double Ps = Math.sqrt((P1 - T1) * (P1 - T1) + (P2 - T2) * (P2 - T2)); double pq = (a + Pr + Ps) / 2; double pr = (b + Pq + Ps) / 2; double ps = (c + Pq + Pr) / 2; double Sa = Math.sqrt(Math.abs(pq * (pq - a) * (pq - Pr) * (pq - Ps))); double Sb = Math.sqrt(Math.abs(pr * (pr - Pq) * (pr - b) * (pr - Ps))); double Sc = Math.sqrt(Math.abs(ps * (ps - Pq) * (ps - Pr) * (ps - c))); if (Math.abs(Sa + Sb + Sc - S) < 0.0000001) { return true; } return false; } static int check1(double a,double b,double c,double x,double y) {//与分割线的位置关系 double res = a * x + b * y + c; if (Math.abs(res) < 0.0000001) { return 0; } else if (res < 0) { return -1; } return 1; } static double Scalc_3(double P1,double P2,double Q1,double Q2,double R1,double R2,double T1,double T2,double S1,double S2){//求三角形的分割面积 double Apq=P2-Q2; double Bpq=Q1-P1; double Cpq=P1*Q2-P2*Q1; double Asr=S2-R2; double Bsr=R1-S1; double Csr=S1*R2-S2*R1; double Art=R2-T2; double Brt=T1-R1; double Crt=R1*T2-R2*T1; double Ast=S2-T2; double Bst=T1-S1; double Cst=S1*T2-S2*T1; double SR=Math.sqrt((S1-R1)*(S1-R1)+(S2-R2)*(S2-R2)); double RT=Math.sqrt((R1-T1)*(R1-T1)+(R2-T2)*(R2-T2)); double ST=Math.sqrt((S1-T1)*(S1-T1)+(S2-T2)*(S2-T2)); double p=(SR+RT+ST)/2; double S=Math.sqrt(p*(p-SR)*(p-ST)*(p-RT)); double Dsr=Apq*Bsr-Asr*Bpq; double Dst=Apq*Bst-Ast*Bpq; double Drt=Apq*Brt-Art*Bpq; if((Math.abs(Dsr)<0.0000001&&Math.abs(Apq*R1+Bpq*R2+Cpq)<0.0000001)||(Math.abs(Dst)<0.0000001&&Math.abs(Apq*S1+Bpq*S2+Cpq)<0.0000001)||(Math.abs(Drt)<0.0000001&&Math.abs(Apq*T1+Bpq*T2+Cpq)<0.0000001)){ System.out.println("The line is coincide with one of the lines"); return 0; } if((check1(Apq,Bpq,Cpq,R1,R2)<0&&check1(Apq,Bpq,Cpq,S1,S2)<0&&check1(Apq,Bpq,Cpq,T1,T2)<0)||(check1(Apq,Bpq,Cpq,R1,R2)>0&&check1(Apq,Bpq,Cpq,S1,S2)>0&&check1(Apq,Bpq,Cpq,T1,T2)>0)){ System.out.println("0"); return 0; } if((check1(Apq,Bpq,Cpq,R1,R2)==0&&check1(Apq,Bpq,Cpq,S1,S2)*check1(Apq,Bpq,Cpq,T1,T2)>0)||(check1(Apq,Bpq,Cpq,S1,S2)==0&&check1(Apq,Bpq,Cpq,R1,R2)*check1(Apq,Bpq,Cpq,T1,T2)>0)||(check1(Apq,Bpq,Cpq,T1,T2)==0&&check1(Apq,Bpq,Cpq,S1,S2)*check1(Apq,Bpq,Cpq,R1,R2)>0)){ System.out.println("1"); return 0; } if((check1(Apq,Bpq,Cpq,R1,R2)<0&&check1(Apq,Bpq,Cpq,S1,S2)>=0&&check1(Apq,Bpq,Cpq,T1,T2)>=0)||(check1(Apq,Bpq,Cpq,R1,R2)>0&&check1(Apq,Bpq,Cpq,S1,S2)<=0&&check1(Apq,Bpq,Cpq,T1,T2)<=0)){ double x1=(Bpq*Csr-Bsr*Cpq)/Dsr; double y1=(Asr*Cpq-Apq*Csr)/Dsr; double x2=(Bpq*Crt-Brt*Cpq)/Drt; double y2=(Art*Cpq-Apq*Crt)/Drt; double l1=Math.sqrt((x1-R1)*(x1-R1)+(y1-R2)*(y1-R2)); double l2=Math.sqrt((x2-R1)*(x2-R1)+(y2-R2)*(y2-R2)); double f=l1*l2/(SR*RT); double rmin=Math.min(S*f,S-S*f); double rmax=Math.max(S*f,S-S*f); BigDecimal smn=new BigDecimal(rmin); BigDecimal smx=new BigDecimal(rmax); rmin=smn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=smx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); return rmin; } else if((check1(Apq,Bpq,Cpq,R1,R2)>=0&&check1(Apq,Bpq,Cpq,S1,S2)<0&&check1(Apq,Bpq,Cpq,T1,T2)>=0)||(check1(Apq,Bpq,Cpq,R1,R2)<=0&&check1(Apq,Bpq,Cpq,S1,S2)>0&&check1(Apq,Bpq,Cpq,T1,T2)<=0)){ double x1=(Bpq*Csr-Bsr*Cpq)/Dsr; double y1=(Asr*Cpq-Apq*Csr)/Dsr; double x2=(Bpq*Cst-Bst*Cpq)/Dst; double y2=(Ast*Cpq-Apq*Cst)/Dst; double l1=Math.sqrt((x1-S1)*(x1-S1)+(y1-S2)*(y1-S2)); double l2=Math.sqrt((x2-S1)*(x2-S1)+(y2-S2)*(y2-S2)); double f=l1*l2/(SR*ST); double rmin=Math.min(S*f,S-S*f); double rmax=Math.max(S*f,S-S*f); BigDecimal smn=new BigDecimal(rmin); BigDecimal smx=new BigDecimal(rmax); rmin=smn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=smx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); return rmin; } else if((check1(Apq,Bpq,Cpq,R1,R2)>=0&&check1(Apq,Bpq,Cpq,S1,S2)>=0&&check1(Apq,Bpq,Cpq,T1,T2)<0)||(check1(Apq,Bpq,Cpq,R1,R2)<=0&&check1(Apq,Bpq,Cpq,S1,S2)<=0&&check1(Apq,Bpq,Cpq,T1,T2)>0)){ double x1=(Bpq*Crt-Brt*Cpq)/Drt; double y1=(Art*Cpq-Apq*Crt)/Drt; double x2=(Bpq*Cst-Bst*Cpq)/Dst; double y2=(Ast*Cpq-Apq*Cst)/Dst; double l1=Math.sqrt((x1-T1)*(x1-T1)+(y1-T2)*(y1-T2)); double l2=Math.sqrt((x2-T1)*(x2-T1)+(y2-T2)*(y2-T2)); double f=l1*l2/(ST*RT); double rmin=Math.min(S*f,S-S*f); double rmax=Math.max(S*f,S-S*f); BigDecimal smn=new BigDecimal(rmin); BigDecimal smx=new BigDecimal(rmax); rmin=smn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=smx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); return rmin; } return 0; } static double Scalc_4(double S1,double S2,double W1,double W2,double P1,double P2,double Q1,double Q2,double R1,double R2,double T1,double T2){//计算四边形的分割面积 double Asw=S2-W2; double Bsw=W1-S1; double Csw=S1*W2-S2*W1; double Apq=P2-Q2; double Bpq=Q1-P1; double Cpq=P1*Q2-P2*Q1; double Art=R2-T2; double Brt=T1-R1; double Crt=R1*T2-R2*T1; double Apt=P2-T2; double Bpt=T1-P1; double Cpt=P1*T2-P2*T1; double Arq=R2-Q2; double Brq=Q1-R1; double Crq=R1*Q2-R2*Q1; double PQ=Math.sqrt((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2)); double QR=Math.sqrt((Q1-R1)*(Q1-R1)+(Q2-R2)*(Q2-R2)); double RT=Math.sqrt((R1-T1)*(R1-T1)+(R2-T2)*(R2-T2)); double PT=Math.sqrt((P1-T1)*(P1-T1)+(P2-T2)*(P2-T2)); double PR=Math.sqrt((P1-R1)*(P1-R1)+(P2-R2)*(P2-R2)); double Dpq=Asw*Bpq-Apq*Bsw; double Drq=Asw*Brq-Arq*Bsw; double Dpt=Asw*Bpt-Apt*Bsw; double Drt=Asw*Brt-Art*Bsw; if((Math.abs(Dpq)<0.0000001&&Math.abs(Asw*P1+Bsw*P2+Csw)<0.0000001)||(Math.abs(Drq)<0.0000001&&Math.abs(Asw*Q1+Bsw*Q2+Csw)<0.0000001)||(Math.abs(Drt)<0.0000001&&Math.abs(Asw*R1+Bsw*R2+Csw)<0.0000001)||(Math.abs(Dpt)<0.0000001&&Math.abs(Asw*T1+Bsw*T2+Csw)<0.0000001)){ System.out.println("The line is coincide with one of the lines"); return 0; } double p1=(PQ+QR+PR)/2; double s1=Math.sqrt(p1*(p1-PQ)*(p1-QR)*(p1-PR)); double p2=(PR+PT+RT)/2; double s2=Math.sqrt(p2*(p2-PR)*(p2-PT)*(p2-RT)); double S_0=s1+s2; int lp=check1(Asw,Bsw,Csw,P1,P2); int lq=check1(Asw,Bsw,Csw,Q1,Q2); int lr=check1(Asw,Bsw,Csw,R1,R2); int lt=check1(Asw,Bsw,Csw,T1,T2); if((lq>0&&lp<=0&&lr<0&<<0)||(lq<0&&lp>=0&&lr>0&<>0)){ double Xpq=(Bsw*Cpq-Bpq*Csw)/Dpq; double Ypq=(Apq*Csw-Asw*Cpq)/Dpq; double Xrq=(Bsw*Crq-Brq*Csw)/Drq; double Yrq=(Arq*Csw-Asw*Crq)/Drq; double l1=Math.sqrt((Xpq-Q1)*(Xpq-Q1)+(Ypq-Q2)*(Ypq-Q2)); double l2=Math.sqrt((Xrq-Q1)*(Xrq-Q1)+(Yrq-Q2)*(Yrq-Q2)); double l3=Math.sqrt((Xpq-Xrq)*(Xpq-Xrq)+(Ypq-Yrq)*(Ypq-Yrq)); double p_1=(l1+l2+l3)/2; double S0=Math.sqrt(p_1*(p_1-l1)*(p_1-l2)*(p_1-l3)); double rmin=Math.min(S0,S_0-S0); double rmax=Math.max(S0,S_0-S0); BigDecimal mn=new BigDecimal(rmin); BigDecimal mx=new BigDecimal(rmax); rmin=mn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=mx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); } else if((lq>0&&lp==0&&lr==0&<<0)||(lq<0&&lp==0&&lr==0&<>0)){ double p_l=(PQ+QR+PR)/2; double p_r=(PR+PT+RT)/2; double s_l=Math.sqrt(p_l*(p_l-PQ)*(p_l-QR)*(p_l-PR)); double s_r=Math.sqrt(p_r*(p_r-PR)*(p_r-PT)*(p_r-RT)); double rmin=Math.min(s_l,s_r); double rmax=Math.max(s_l,s_r); BigDecimal mn=new BigDecimal(rmin); BigDecimal mx=new BigDecimal(rmax); rmin=mn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=mx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); } else if((lq>0&&lp>0&<<0&&lr<0)||(lq<0&&lp<0&<>0&&lr>0)){ double Xpt=(Bsw*Cpt-Bpt*Csw)/Dpt; double Ypt=(Apt*Csw-Asw*Cpt)/Dpt; double Xrq=(Bsw*Crq-Brq*Csw)/Drq; double Yrq=(Arq*Csw-Asw*Crq)/Drq; double AQ=Math.sqrt((Xpt-Q1)*(Xpt-Q1)+(Ypt-Q2)*(Ypt-Q2)); double AR=Math.sqrt((Xpt-R1)*(Xpt-R1)+(Ypt-R2)*(Ypt-R2)); double AP=Math.sqrt((Xpt-P1)*(Xpt-P1)+(Ypt-P2)*(Ypt-P2)); double AT=Math.sqrt((Xpt-T1)*(Xpt-T1)+(Ypt-T2)*(Ypt-T2)); double BQ=Math.sqrt((Xrq-Q1)*(Xrq-Q1)+(Yrq-Q2)*(Yrq-Q2)); double BR=Math.sqrt((Xrq-R1)*(Xrq-R1)+(Yrq-R2)*(Yrq-R2)); double AB=Math.sqrt((Xpt-Xrq)*(Xpt-Xrq)+(Ypt-Yrq)*(Ypt-Yrq)); double pl1=(AP+PQ+AQ)/2; double pl2=(AQ+BQ+AB)/2; double pr1=(AT+RT+AR)/2; double pr2=(AB+AR+BR)/2; double Sl=Math.sqrt(pl1*(pl1-AP)*(pl1-PQ)*(pl1-AQ))+Math.sqrt(pl2*(pl2-AQ)*(pl2-BQ)*(pl2-AB)); double Sr=Math.sqrt(pr1*(pr1-AT)*(pr1-RT)*(pr1-AR))+Math.sqrt(pr2*(pr2-AB)*(pr2-AR)*(pr2-BR)); double rmin=Math.min(Sl,Sr); double rmax=Math.max(Sl,Sr); BigDecimal mn=new BigDecimal(rmin); BigDecimal mx=new BigDecimal(rmax); rmin=mn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=mx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); } else if((lp==1&&lq==1&&lr>=0&<<0)||(lp==-1&&lq==-1&&lr<=0&<>0)){ double Xpt=(Bsw*Cpt-Bpt*Csw)/Dpt; double Ypt=(Apt*Csw-Asw*Cpt)/Dpt; double Xrt=(Bsw*Crt-Brt*Csw)/Drt; double Yrt=(Art*Csw-Asw*Crt)/Drt; double AB=Math.sqrt((Xpt-Xrt)*(Xpt-Xrt)+(Ypt-Yrt)*(Ypt-Yrt)); double AT=Math.sqrt((Xpt-T1)*(Xpt-T1)+(Ypt-T2)*(Ypt-T2)); double BT=Math.sqrt((Xrt-T1)*(Xrt-T1)+(Yrt-T2)*(Yrt-T2)); double p=(AB+AT+BT)/2; double Sr=Math.sqrt(p*(p-AB)*(p-AT)*(p-BT)); double Sl=S_0-Sr; double rmin=Math.min(Sl,Sr); double rmax=Math.max(Sl,Sr); BigDecimal mn=new BigDecimal(rmin); BigDecimal mx=new BigDecimal(rmax); rmin=mn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=mx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); } return 0; } static double Scalc_4o(double S1,double S2,double W1,double W2,double P1,double P2,double Q1,double Q2,double R1,double R2,double T1,double T2){//求凹四边形的分割面积(其实并不需要) double Asw=S2-W2; double Bsw=W1-S1; double Csw=S1*W2-S2*W1; double Apq=P2-Q2; double Bpq=Q1-P1; double Cpq=P1*Q2-P2*Q1; double Art=R2-T2; double Brt=T1-R1; double Crt=R1*T2-R2*T1; double Apt=P2-T2; double Bpt=T1-P1; double Cpt=P1*T2-P2*T1; double Arq=R2-Q2; double Brq=Q1-R1; double Crq=P1*Q2-P2*Q1; double PQ=Math.sqrt((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2)); double QR=Math.sqrt((Q1-R1)*(Q1-R1)+(Q2-R2)*(Q2-R2)); double RT=Math.sqrt((R1-T1)*(R1-T1)+(R2-T2)*(R2-T2)); double PT=Math.sqrt((P1-T1)*(P1-T1)+(P2-T2)*(P2-T2)); double QT=Math.sqrt((Q1-T1)*(Q1-T1)+(Q2-T2)*(Q2-T2)); double Dpq=Asw*Bpq-Apq*Bsw; double Drq=Asw*Brq-Arq*Bsw; double Dpt=Asw*Bpt-Apt*Bsw; double Drt=Asw*Brt-Art*Bsw; if((Math.abs(Dpq)<0.0000001&&Math.abs(Asw*P1+Bsw*P2+Csw)<0.0000001)||(Math.abs(Drq)<0.0000001&&Math.abs(Asw*Q1+Bsw*Q2+Csw)<0.0000001)||(Math.abs(Drt)<0.0000001&&Math.abs(Asw*R1+Bsw*R2+Csw)<0.0000001)||(Math.abs(Dpt)<0.0000001&&Math.abs(Asw*T1+Bsw*T2+Csw)<0.0000001)){ System.out.println("The line is coincide with one of the lines"); return 0; } double Xpt=(Bsw*Cpt-Bpt*Csw)/Dpt; double Ypt=(Apt*Csw-Asw*Cpt)/Dpt; double Xrt=(Bsw*Crt-Brt*Csw)/Dpt; double Yrt=(Art*Csw-Asw*Crt)/Drt; double p1=(PT+PQ+QT)/2; double p2=(QT+QR+RT)/2; double s1=Math.sqrt(p1*(p1-PT)*(p1-PQ)*(p1-QT)); double s2=Math.sqrt(p2*(p2-QT)*(p2-QR)*(p2-RT)); double s_0=s1+s2; if((check1(Asw,Bsw,Csw,Q1,Q2)>=0&&check1(Asw,Bsw,Csw,T1,T2)<0)||(check1(Asw,Bsw,Csw,Q1,Q2)<=0&&check1(Asw,Bsw,Csw,T1,T2)>0)) { double AT = Math.sqrt((Xpt - T1) * (Xpt - T1) + (Ypt - T2) * (Ypt - T2)); double BT = Math.sqrt((Xrt - T1) * (Xrt - T1) + (Yrt - T2) * (Yrt - T2)); double AB = Math.sqrt((Xpt - Xrt) * (Xpt - Xrt) + (Ypt - Yrt) * (Ypt - Yrt)); double p3 = (AT + BT + AB) / 2; double s3 = Math.sqrt(p3 * (p3 - AT) * (p3 - BT) * (p3 - AB)); double rmin = Math.min(s3, s_0 - s3); double rmax = Math.max(s3, s_0 - s3); BigDecimal mn = new BigDecimal(rmin); BigDecimal mx = new BigDecimal(rmax); rmin = mn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = mx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } else if((check1(Asw,Bsw,Csw,Q1,Q2)>=0&&check1(Asw,Bsw,Csw,T1,T2)>0)||(check1(Asw,Bsw,Csw,Q1,Q2)<=0&&check1(Asw,Bsw,Csw,T1,T2)<0)){ if(check1(Asw,Bsw,Csw,T1,T2)*check1(Asw,Bsw,Csw,R1,R2)<0) { double Xrq = (Bsw * Crq - Brq * Csw) / Drq; double Yrq = (Arq * Csw - Asw * Crq) / Drq; double AR = Math.sqrt((Xrq - R1) * (Xrq - R1) + (Yrq - R2) * (Yrq - R2)); double BR = Math.sqrt((Xrt - R1) * (Xrt - R2) + (Yrt - R1) * (Yrt - R2)); double AB = Math.sqrt((Xrq - Xrt) * (Xrq - Xrt) + (Yrq - Yrt) * (Yrq - Yrt)); double p3 = (AB + AR + BR) / 2; double s3 = Math.sqrt(p3 * (p3 - AB) * (p3 - AR) * (p3 - BR)); double rmin = Math.min(s3, s_0 - s3); double rmax = Math.max(s3, s_0 - s3); BigDecimal mn = new BigDecimal(rmin); BigDecimal mx = new BigDecimal(rmax); rmin = mn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = mx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } else if(check1(Asw,Bsw,Csw,T1,T2)*check1(Asw,Bsw,Csw,P1,P2)<0){ double Xpq=(Bsw*Cpq-Bpq*Csw)/Dpq; double Ypq=(Apq*Csw-Asw*Cpq)/Dpq; double AP=Math.sqrt((Xpq-P1)*(Xpq-P1)+(Ypq-P2)*(Ypq-P2)); double BP=Math.sqrt((Xpt-P1)*(Xpq-P1)+(Ypt-P2)*(Ypt-P2)); double AB=Math.sqrt((Xpq-Xpt)*(Xpq-Xpt)+(Ypq-Ypt)*(Ypq-Ypt)); double p3=(AB+AP+BP)/2; double s3=Math.sqrt(p3*(p3-AB)*(p3-AP)*(p3-BP)); double rmin = Math.min(s3, s_0 - s3); double rmax = Math.max(s3, s_0 - s3); BigDecimal mn = new BigDecimal(rmin); BigDecimal mx = new BigDecimal(rmax); rmin = mn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = mx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } } else if(check1(Asw,Bsw,Csw,T1,T2)==0){ if(check1(Asw,Bsw,Csw,P1,P2)*check1(Asw,Bsw,Csw,Q1,Q2)<0){ double Xpq=(Bsw*Cpq-Bpq*Csw)/Dpq; double Ypq=(Apq*Csw-Asw*Cpq)/Dpq; double AT=Math.sqrt((Xpq-T1)*(Xpq-T1)+(Ypq-T2)*(Ypq-T2)); double AP=Math.sqrt((Xpq-P1)*(Xpq-P1)+(Ypq-P2)*(Ypq-P2)); double p3=(AT+AP+PT)/2; double s3=Math.sqrt(p3*(p3-AT)*(p3-AP)*(p3-PT)); double rmin = Math.min(s3, s_0 - s3); double rmax = Math.max(s3, s_0 - s3); BigDecimal mn = new BigDecimal(rmin); BigDecimal mx = new BigDecimal(rmax); rmin = mn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = mx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } else{ double Xrq=(Bsw*Crq-Brq*Csw)/Drq; double Yrq=(Arq*Csw-Asw*Crq)/Drq; double AT=Math.sqrt((Xrq-T1)*(Xrq-T1)+(Yrq-T2)*(Yrq-T2)); double AR=Math.sqrt((Xrq-R1)*(Xrq-R1)+(Yrq-R2)*(Yrq-R2)); double p3=(AT+AR+RT)/2; double s3=Math.sqrt(p3*(p3-AT)*(p3-AR)*(p3-RT)); double rmin = Math.min(s3, s_0 - s3); double rmax = Math.max(s3, s_0 - s3); BigDecimal mn = new BigDecimal(rmin); BigDecimal mx = new BigDecimal(rmax); rmin = mn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = mx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } } return 0; } static double dis(double a,double b,double c,double x,double y) {//求点与直线的距离 double d = Math.sqrt(a * a + b * b); double e = a * x + b * y + c; return e / d; } static boolean check2(double P1,double P2,double Q1,double Q2,double R1,double R2,double T1,double T2){//两直线是否相交 double Apq=P2-Q2; double Bpq=Q1-P1; double Cpq=P1*Q2-P2*Q1; double Art=R2-T2; double Brt=T1-R1; double Crt=R1*T2-R2*T1; double Arq=R2-Q2; double Brq=Q1-R1; double Crq=R1*Q2-R2*Q1; double Apt=P2-T2; double Bpt=T1-P1; double Cpt=P1*T2-P2*T1; double Dpq_rt=Apq*Brt-Art*Bpq; double Dpt_qr=Apt*Brq-Arq*Bpt; if(Dpt_qr!=0){ double Xpt_rq=(Bpt*Crq-Brq*Cpt)/Dpt_qr; double Ypt_rq=(Arq*Cpt-Apt*Crq)/Dpt_qr; if((Xpt_rq>Math.min(P1,T1)&&Xpt_rq<Math.max(P1,T1)&&Ypt_rq>=Math.min(P2,T2)&&Ypt_rq<=Math.max(P2,T2))||(Xpt_rq>=Math.min(P1,T1)&&Xpt_rq<=Math.max(P1,T1)&&Ypt_rq>Math.min(P2,T2)&&Ypt_rq<Math.max(P2,T2))){ return false; } } if(Dpq_rt!=0){ double Xpq_rt=(Bpq*Crt-Brt*Cpq)/Dpq_rt; double Ypq_rt=(Art*Cpq-Apq*Crt)/Dpq_rt; if((Xpq_rt>Math.min(P1,Q1)&&Xpq_rt<Math.max(P1,Q1)&&Ypq_rt>=Math.min(P2,Q2)&&Ypq_rt<=Math.max(P2,Q2))||(Xpq_rt>=Math.min(P1,Q1)&&Xpq_rt<=Math.max(P1,Q1)&&Ypq_rt>Math.min(P2,Q2)&&Ypq_rt<Math.max(P2,Q2))){ return false; } } return true; } static boolean check3(double P1,double P2,double Q1,double Q2,double R1,double R2){//点是否在直线上 double Apq=Q2-P2; double Bpq=P1-Q1; double Cpq=P1*Q2-P2*Q1; double res=Apq*R1+Bpq*R2+Cpq; if(Math.abs(res)<0.0000001){ return true; } return false; } }
最后一个没有用类的题。分析一下吧~
sourcemonitor分析:
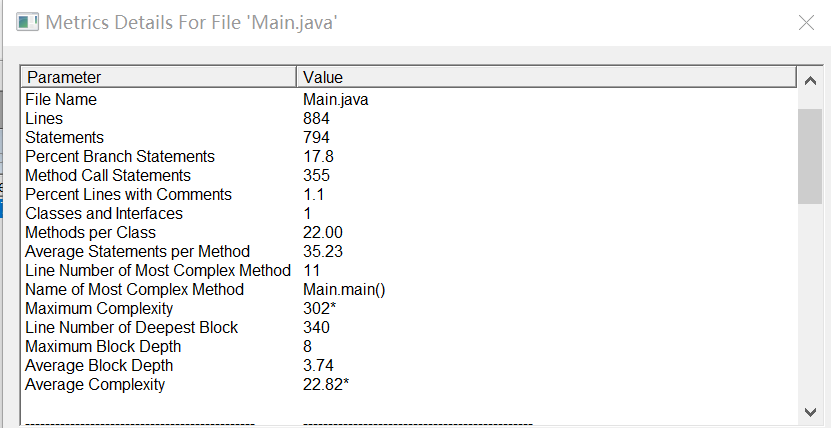
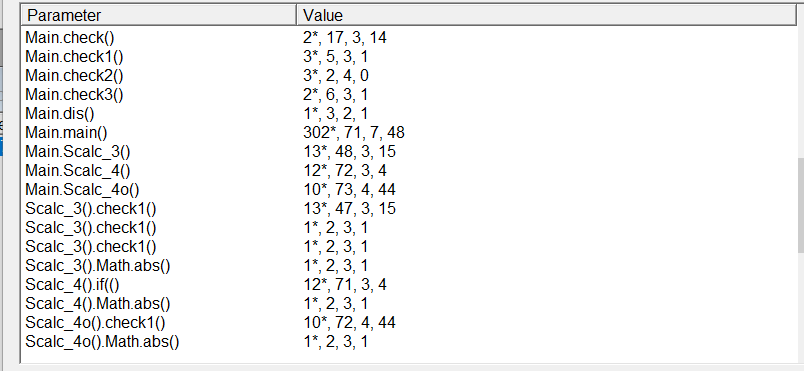

由于缺少类的使用,该份代码复杂度高,总体质量仍然不高。函数的调用倒是大幅缩短了代码量。
总结:三角形升级版,注意细节,耐心计算即可AC。
第四次大作业T3
题面:
编写一个银行业务类BankBusiness,具有以下属性和方法:
(1)公有、静态的属性:银行名称bankName,初始值为“中国银行”。
(2)私有属性:账户名name、密码password、账户余额balance。
(3)银行对用户到来的欢迎(welcome)动作(静态、公有方法),显示“中国银行欢迎您的到来!”,其中“中国银行”自动使用bankName的值。
(4)银行对用户离开的提醒(welcomeNext)动作(静态、公有方法),显示“请收好您的证件和物品,欢迎您下次光临!”
(5)带参数的构造方法,完成开户操作。需要账户名name、密码password信息,同时让账户余额为0。
(6)用户的存款(deposit)操作(公有方法,需要密码和交易额信息),密码不对时无法存款且提示“您的密码错误!”;密码正确、完成用户存款操作后,要提示用户的账户余额,例如“您的余额有1000.0元。”。
(7)用户的取款(withdraw)操作(公有方法,需要密码和交易额信息)。密码不对时无法取款且提示“您的密码错误!”;密码正确但余额不足时提示“您的余额不足!”;密码正确且余额充足时扣除交易额并提示用户的账户余额,例如“请取走钞票,您的余额还有500.0元。”。
编写一个测试类Main,在main方法中,先后执行以下操作:
(1)调用BankBusiness类的welcome()方法。
(2)接收键盘输入的用户名、密码信息作为参数,调用BankBusiness类带参数的构造方法,从而创建一个BankBusiness类的对象account。
(3)调用account的存款方法,输入正确的密码,存入若干元。密码及存款金额从键盘输入。
(4)调用account的取款方法,输入错误的密码,试图取款若干元。密码及取款金额从键盘输入。
(5)调用account的取款方法,输入正确的密码,试图取款若干元(取款金额大于余额)。密码及取款金额从键盘输入。
(6)调用account的取款方法,输入正确的密码,试图取款若干元(取款金额小于余额)。密码及取款金额从键盘输入。
(7)调用BankBusiness类的welcomeNext()方法。
输入格式:
输入开户需要的姓名、密码
输入正确密码、存款金额
输入错误密码、取款金额
输入正确密码、大于余额的取款金额
输入正确密码、小于余额的取款金额
输出格式:
中国银行(银行名称)欢迎您的到来!
您的余额有多少元。
您的密码错误!
您的余额不足!
请取走钞票,您的余额还有多少元。
请收好您的证件和物品,欢迎您下次光临!
输入样例:
在这里给出一组输入。请注意,输入与输出是交替的,具体顺序请看测试类中的说明。例如:
张三 123456
123456 1000
654321 2000
123456 2000
123456 500输出样例:
在这里给出相应的输出。请注意,输入与输出是交替的,具体顺序请看测试类中的说明。例如:
中国银行欢迎您的到来!
您的余额有1000.0元。
您的密码错误!
您的余额不足!
请取走钞票,您的余额还有500.0元。
请收好您的证件和物品,欢迎您下次光临!一道非常简单的题,直接按题意模拟即可。T1、本题和T2相比真是小巫见大巫。
上代码喽!
import java.util.*; import java.text.DecimalFormat; import java.io.*; import java.lang.*; import java.math.*; import java.net.*; import java.text.*; import java.text.NumberFormat; class User{//用户类 String name; String password; float balance; } class Bankbusiness{//银行业务类 String bname; User user=new User(); void welcome1(){ System.out.println("中国银行欢迎您的到来!"); } void welcome2(String a,String b){ user.name=a; user.password=b; user.balance=0; } void in(String t,float num){ boolean flag=true; int n=t.length(),m=user.password.length(); if(n!=m){ flag=false; } else{ for(int i=0;i<n;i++){ if(t.charAt(i)!=user.password.charAt(i)){ flag=false; } } } if(flag){ user.balance+=num; System.out.printf("您的余额有%.1f元。\n",user.balance); } else{ System.out.println("您的密码错误!"); } } void out(String t,float num){ boolean flag=true; int n=t.length(),m=user.password.length(); if(n!=m){ flag=false; } else{ for(int i=0;i<n;i++){ if(t.charAt(i)!=user.password.charAt(i)){ flag=false; } } } if(flag){ if(num>user.balance){ System.out.println("您的余额不足!"); } else{ user.balance-=num; System.out.printf("请取走钞票,您的余额还有%.1f元。\n",user.balance); } } else{ System.out.println("您的密码错误!"); } } void welcomeNext(){ System.out.println("请收好您的证件和物品,欢迎您下次光临!"); } } public class Main{ public static void main(String[] args){ Scanner bjsn=new Scanner(System.in); Bankbusiness account=new Bankbusiness(); account.welcome1(); String wec=bjsn.nextLine(); String namee="",pass=""; int pos=0,n=wec.length(); for(int i=0;i<n;i++){ if(wec.charAt(i)==' '){ pos=i; break; } } for(int i=0;i<pos;i++){ namee+=wec.charAt(i); } for(int i=pos+1;i<n;i++){ pass+=wec.charAt(i); } account.welcome2(namee,pass); for(int t=0;t<4;t++){ namee=""; pass=""; String s=bjsn.nextLine(); n=s.length(); for(int i=0;i<n;i++){ if(s.charAt(i)==' '){ pos=i; break; } } for(int i=0;i<pos;i++){ namee+=s.charAt(i); } for(int i=pos+1;i<n;i++){ pass+=s.charAt(i); } float cnt=Float.parseFloat(pass); switch(t){ case 0:account.in(namee,cnt); break; case 1: case 2: case 3:account.out(namee,cnt); break; } } account.welcomeNext(); } }
和T1差不多的难度,这里就不做sourcemonitor分析啦!
同时,本题为历次大作业中第一道用类写的题。
第五次大作业T1
题面:
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
以上3选项中,若输入的点无法构成多边形,则输出"not a polygon"。输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例1:
选项1,点重合。例如:
1:-1,-1 1,2 -1,1 1,0输出样例:
在这里给出相应的输出。例如:
wrong number of points
第五次大作业,传说中最难的一次大作业,果然题目看上去就让人头大啊!
首先整理一下思路:
case1、case2当然没什么好说的,主要分析T3。
仔细一想,可能是三角形,四边形,也可能是五边形。
情况太多了吧!还要判断重点!
这时候,LinkedHashList派上用场了。LinkedHashList可以在不打乱原有顺序的情况下对整个序列进行去重。
然后再分类讨论:
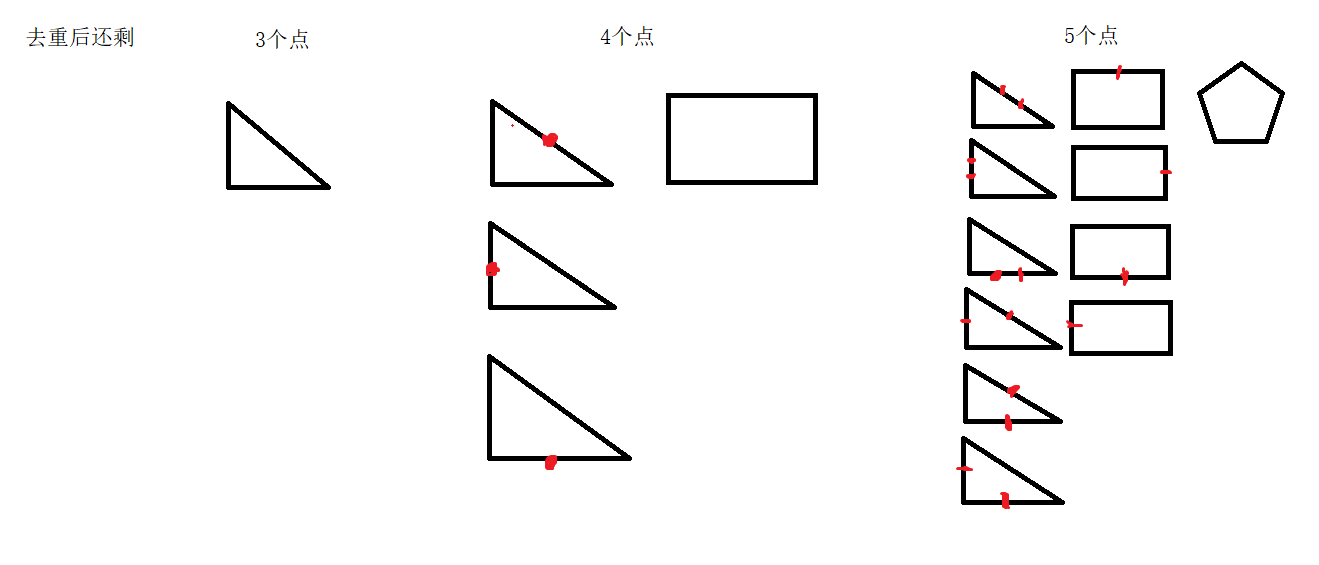
至于求面积,思路和第四次大作业T2差不多。

我滴代码
import java.util.*; import java.io.*; import java.lang.*; import java.math.*; import java.net.*; import java.text.*; public class Main{ static double x1=0,y1=0,x2=0,y2=0,x3=0,y3=0,x4=0,y4=0,x5=0,y5=0,x6=0,y6=0,x7=0,y7=0; static Point t; public static void main(String[] args){ Scanner bjsn=new Scanner(System.in); String s=bjsn.nextLine(); int len=s.length(); int cnt=0; //基本格式判断 if(len==10){ System.out.println("Wrong Format"); return; } for(int i=0;i<len;i++){ if(s.charAt(i)==','){ cnt++; } } for(int i=1;i<len;i++){ if(s.charAt(i)==','&&s.charAt(i-1)==','){ System.out.println("Wrong Format"); return; } } if(cnt==0){ System.out.println("Wrong Format"); return; } if(s.charAt(0)<'1'||s.charAt(0)>'3'||s.charAt(1)!=':'||(s.charAt(len-1)<'0'||s.charAt(len-1)>'9')){ System.out.println("Wrong Format"); return; } int pos=2; if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){ System.out.println("Wrong Format"); return; } if(s.charAt(2)=='-'&&s.charAt(15)=='-'){ System.out.println("Wrong Format"); return; } String sss=s.substring(2,len); String ss[]=sss.split(" "); String str[]=null; for(String Str:ss){//正则输入法判断格式并提取数字 str=Str.split(","); for(String tt:str){ if(!tt.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){ System.out.println("Wrong Format"); return; } } } Line line = new Line(); Trangle trangle = new Trangle(); Quadrilateral quadrilateral = new Quadrilateral(); Pentagon pentagon = new Pentagon(); switch (s.charAt(0)){ case '1': if(ss.length!=5) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str=ss[0].split(",");x1=Double.parseDouble(str[0]);y1=Double.parseDouble(str[1]); str=ss[1].split(",");x2=Double.parseDouble(str[0]);y2=Double.parseDouble(str[1]); str=ss[2].split(",");x3=Double.parseDouble(str[0]);y3=Double.parseDouble(str[1]); str=ss[3].split(",");x4=Double.parseDouble(str[0]);y4=Double.parseDouble(str[1]); str=ss[4].split(",");x5=Double.parseDouble(str[0]);y5=Double.parseDouble(str[1]); if(line.cross(x1,y1,x2,y2,x3,y3,x4,y4)||line.cross(x1,y1,x2,y2,x4,y4,x5,y5)||line.cross(x2,y2,x3,y3,x4,y4,x5,y5)||line.cross(x2,y2,x3,y3,x1,y1,x5,y5)||line.cross(x3,y3,x4,y4,x1,y1,x5,y5)||line.cross(x3,y3,x4,y4,x1,y1,x2,y2)||line.cross(x4,y4,x5,y5,x1,y1,x2,y2)||line.cross(x4,y4,x5,y5,x2,y2,x3,y3)||line.cross(x5,y5,x1,y1,x2,y2,x3,y3)||line.cross(x5,y5,x1,y1,x3,y3,x4,y4)){ System.out.println("false");//只要有相交就不算 return; } if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)||line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)||line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)||line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)||line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ System.out.println("false");//只要有平行就不算 return; } System.out.println("true"); break; case '2': if(ss.length!=5) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str=ss[0].split(",");x1=Double.parseDouble(str[0]);y1=Double.parseDouble(str[1]); str=ss[1].split(",");x2=Double.parseDouble(str[0]);y2=Double.parseDouble(str[1]); str=ss[2].split(",");x3=Double.parseDouble(str[0]);y3=Double.parseDouble(str[1]); str=ss[3].split(",");x4=Double.parseDouble(str[0]);y4=Double.parseDouble(str[1]); str=ss[4].split(",");x5=Double.parseDouble(str[0]);y5=Double.parseDouble(str[1]); if(line.cross(x1,y1,x2,y2,x3,y3,x4,y4)||line.cross(x1,y1,x2,y2,x4,y4,x5,y5)||line.cross(x2,y2,x3,y3,x4,y4,x5,y5)||line.cross(x2,y2,x3,y3,x1,y1,x5,y5)||line.cross(x3,y3,x4,y4,x1,y1,x5,y5)){ System.out.println("not a pentagon"); return; } if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)&&line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ System.out.println("not a pentagon"); return; } if((line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&!line.check(x1,y1,x2,y2,x3,y3))||(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&!line.check(x2,y2,x3,y3,x4,y4))||(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)&&!line.check(x3,y3,x4,y4,x5,y5))||(line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)&&!line.check(x4,y4,x5,y5,x1,y1))||(line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)&&!line.check(x5,y5,x1,y1,x2,y2))){ System.out.println("not a pentagon"); return; } if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)||line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)||line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)||line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)||line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ System.out.println("not a pentagon"); return; } if(line.isPointCoincide(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)>0){ System.out.println("not a pentagon"); return; }//枚举第五个点,看它是否在由前四个点组成的四边形中,如在则为凹四边形 if(pentagon.isTPentagon(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)&& pentagon.isTPentagon(x1,y1,x3,y3,x4,y4,x5,y5,x2,y2)&& pentagon.isTPentagon(x1,y1,x2,y2,x4,y4,x5,y5,x3,y3)&& pentagon.isTPentagon(x1,y1,x2,y2,x3,y3,x5,y5,x4,y4)&& pentagon.isTPentagon(x2,y2,x3,y3,x4,y4,x5,y5,x1,y1)){ double C=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))+Math.sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3))+Math.sqrt((x3-x4)*(x3-x4)+(y3-y4)*(y3-y4))+Math.sqrt((x4-x5)*(x4-x5)+(y4-y5)*(y4-y5))+Math.sqrt((x1-x5)*(x1-x5)+(y1-y5)*(y1-y5)); double S= trangle.qinjiushao(x1,y1,x2,y2,x3,y3)+ trangle.qinjiushao(x1,y1,x3,y3,x4,y4)+ trangle.qinjiushao(x1,y1,x4,y4,x5,y5); BigDecimal Cc= new BigDecimal(C); BigDecimal Ss= new BigDecimal(S); C=Cc.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); S=Ss.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("true "+C+" "+S); } else{ System.out.println("false"); } break; case '3': if(ss.length!=7) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str=ss[0].split(",");x6=Double.parseDouble(str[0]);y6=Double.parseDouble(str[1]); str=ss[1].split(",");x7=Double.parseDouble(str[0]);y7=Double.parseDouble(str[1]); str=ss[2].split(",");x1=Double.parseDouble(str[0]);y1=Double.parseDouble(str[1]); str=ss[3].split(",");x2=Double.parseDouble(str[0]);y2=Double.parseDouble(str[1]); str=ss[4].split(",");x3=Double.parseDouble(str[0]);y3=Double.parseDouble(str[1]); str=ss[5].split(",");x4=Double.parseDouble(str[0]);y4=Double.parseDouble(str[1]); str=ss[6].split(",");x5=Double.parseDouble(str[0]);y5=Double.parseDouble(str[1]); if(line.cross(x1,y1,x2,y2,x3,y3,x4,y4)||line.cross(x1,y1,x2,y2,x4,y4,x5,y5)||line.cross(x2,y2,x3,y3,x4,y4,x5,y5)||line.cross(x2,y2,x3,y3,x1,y1,x5,y5)||line.cross(x3,y3,x4,y4,x1,y1,x5,y5)||line.cross(x3,y3,x4,y4,x1,y1,x2,y2)||line.cross(x4,y4,x5,y5,x1,y1,x2,y2)||line.cross(x4,y4,x5,y5,x2,y2,x3,y3)||line.cross(x5,y5,x1,y1,x2,y2,x3,y3)||line.cross(x5,y5,x1,y1,x3,y3,x4,y4)){ System.out.println("not a pentagon"); return; } if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)&&line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ System.out.println("not a pentagon"); return; } if(line.isPointCoincide(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)>3){ System.out.println("not a pentagon"); return; } if(line.pointCoincide(x6,y6,x7,y7)){ System.out.println("points coincide"); return; } if(line.lineCoincide(x1,y1,x2,y2,x6,y6,x7,y7)||line.lineCoincide(x2,y2,x3,y3,x6,y6,x7,y7)||line.lineCoincide(x3,y3,x4,y4,x6,y6,x7,y7)||line.lineCoincide(x4,y4,x5,y5,x6,y6,x7,y7)||line.lineCoincide(x1,y1,x5,y5,x6,y6,x7,y7)){ System.out.println("The line is coincide with one of the lines"); return; } if((line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0&&line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x5,y5)<=0)||(line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0&&line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x5,y5)>=0)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x3,y3)<0&&line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x5,y5)<0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x3,y3)>0&&line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x5,y5)>0)) { System.out.println("0"); } else{ System.out.println("1"); } return; } if(line.isPointCoincide(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)==2||line.isPointCoincide(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)==3){ LinkedHashSet<Point>set = new LinkedHashSet<>(); set.add(new Point(x1,y1)); set.add(new Point(x2,y2)); set.add(new Point(x3,y3)); set.add(new Point(x4,y4)); set.add(new Point(x5,y5)); Point zb[] = new Point[3]; int posIndex=0; for(Point k:set){ zb[posIndex++]=k; } x1=zb[0].x;y1=zb[0].y; x2=zb[1].x;y2=zb[1].y; x3=zb[2].x;y3=zb[2].y; if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x1,y1,x2,y2,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x2,y2,x1,y1,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x2,y2,x1,y1,x6,y6,x7,y7); } } else if(line.isPointCoincide(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)==1){ LinkedHashSet<Point>set = new LinkedHashSet<>(); set.add(new Point(x1,y1)); set.add(new Point(x2,y2)); set.add(new Point(x3,y3)); set.add(new Point(x4,y4)); set.add(new Point(x5,y5)); Point zb[] = new Point[4]; int posIndex=0; for(Point k:set){ zb[posIndex++]=k; } x1=zb[0].x;y1=zb[0].y; x2=zb[1].x;y2=zb[1].y; x3=zb[2].x;y3=zb[2].y; x4=zb[3].x;y4=zb[3].y; if(line.numParad(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)==3){ if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0&&line.loc(x6,y6,x7,y7,x4,y4)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0&&line.loc(x6,y6,x7,y7,x4,y4)<=0)){ trangle.sTrangle(x1,y1,x3,y3,x4,y4,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x3,y3)<0&&line.loc(x6,y6,x7,y7,x4,y4)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x3,y3)>0&&line.loc(x6,y6,x7,y7,x4,y4)<=0)){ trangle.sTrangle(x3,y3,x1,y1,x4,y4,x6,y6,x7,y7); } else{ trangle.sTrangle(x4,y4,x3,y3,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x4,y4)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x4,y4)<=0)){ trangle.sTrangle(x1,y1,x2,y2,x4,y4,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x4,y4)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x4,y4)<=0)){ trangle.sTrangle(x2,y2,x1,y1,x4,y4,x6,y6,x7,y7); } else{ trangle.sTrangle(x4,y4,x2,y2,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x3,y3,x4,y4,x4,y4,x1,y1)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x1,y1,x2,y2,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x2,y2,x1,y1,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x2,y2,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x4,y4,x1,y1,x1,y1,x2,y2)){ if((line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x4,y4,x2,y2,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x2,y2,x4,y4,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x2,y2,x4,y4,x6,y6,x7,y7); } } } else { quadrilateral.getQua(x1,y1,x2,y2,x3,y3,x4,y4,x6,y6,x7,y7); } } else{ if(line.numParad(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)==2){ if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x5,y5)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x5,y5)<=0)){ trangle.sTrangle(x1,y1,x4,y4,x5,y5,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x5,y5)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x5,y5)<=0)){ trangle.sTrangle(x4,y4,x1,y1,x5,y5,x6,y6,x7,y7); } else{ trangle.sTrangle(x5,y5,x4,y4,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x5,y5)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x5,y5)<=0)){ trangle.sTrangle(x1,y1,x2,y2,x5,y5,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x5,y5)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x5,y5)<=0)){ trangle.sTrangle(x2,y2,x1,y1,x5,y5,x6,y6,x7,y7); } else{ trangle.sTrangle(x5,y5,x2,y2,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x1,y1,x2,y2,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x2,y2,x1,y1,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x2,y2,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)&&line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ if((line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x4,y4,x2,y2,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x2,y2)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x2,y2)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x2,y2,x4,y4,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x2,y2,x4,y4,x6,y6,x7,y7); } } else if(line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)&&line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ if((line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x5,y5)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x5,y5)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x4,y4,x5,y5,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x5,y5)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x5,y5)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x5,y5,x4,y4,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x5,y5,x4,y4,x6,y6,x7,y7); } } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x5,y5)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x5,y5)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x1,y1,x5,y5,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x5,y5)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x5,y5)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x5,y5,x1,y1,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x5,y5,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x1,y1,x5,y5,x5,y5,x4,y4)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x1,y1,x4,y4,x3,y3,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x3,y3)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x3,y3)<=0)){ trangle.sTrangle(x4,y4,x1,y1,x3,y3,x6,y6,x7,y7); } else{ trangle.sTrangle(x3,y3,x4,y4,x1,y1,x6,y6,x7,y7); } } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x1,y1,x5,y5,x5,y5,x4,y4)){ if((line.loc(x6,y6,x7,y7,x1,y1)<0&&line.loc(x6,y6,x7,y7,x4,y4)>=0&&line.loc(x6,y6,x7,y7,x2,y2)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)>0&&line.loc(x6,y6,x7,y7,x4,y4)<=0&&line.loc(x6,y6,x7,y7,x2,y2)<=0)){ trangle.sTrangle(x1,y1,x4,y4,x2,y2,x6,y6,x7,y7); } else if((line.loc(x6,y6,x7,y7,x1,y1)>=0&&line.loc(x6,y6,x7,y7,x4,y4)<0&&line.loc(x6,y6,x7,y7,x2,y2)>=0)||(line.loc(x6,y6,x7,y7,x1,y1)<=0&&line.loc(x6,y6,x7,y7,x4,y4)>0&&line.loc(x6,y6,x7,y7,x2,y2)<=0)){ trangle.sTrangle(x4,y4,x1,y1,x2,y2,x6,y6,x7,y7); } else{ trangle.sTrangle(x2,y2,x4,y4,x1,y1,x6,y6,x7,y7); } } } else if(line.numParad(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)==1){ if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ quadrilateral.getQua(x1,y1,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7); } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ quadrilateral.getQua(x1,y1,x2,y2,x4,y4,x5,y5,x6,y6,x7,y7); } else if(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ quadrilateral.getQua(x1,y1,x2,y2,x3,y3,x5,y5,x6,y6,x7,y7); } else if(line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)){ quadrilateral.getQua(x1,y1,x2,y2,x3,y3,x4,y4,x6,y6,x7,y7); } else if(line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ quadrilateral.getQua(x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7); } } else{ pentagon.getPen(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7); } } } } } class Point{//点类 double x,y; public Point(double x,double y){ this.x=x; this.y=y; } @Override public boolean equals(Object t){//判重 if(this == t){ return true; } if(t == null || getClass() != t.getClass()){ return false; } Point point = (Point) t; return x == point.x && y == point.y &&Objects.equals(x,point.x) && Objects.equals(y,point.y); } @Override public int hashCode(){//重写hash函数 return Objects.hash(x,y); } } class Line{//线类 boolean check(double x1,double y1,double x2,double y2,double x3,double y3){//点是否在线段上 if(isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ if((x2>x1&&x3<x2)||(x2<x1&&x3>x2)){ return false; } } return true; } boolean cross(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//判断是否相交 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A34=y3-y4; double B34=x4-x3; double C34=x3*y4-x4*y3; double D=A12*B34-A34*B12; if(Math.abs(D)>=0.0000001){ double x=(B12*C34-B34*C12)/D; double y=(A34*C12-A12*C34)/D; if(x<Math.max(x1,x2)&&x>Math.min(x1,x2)&&y<Math.max(y1,y2)&&y>Math.min(y1,y2)){ return true; } } return false; } boolean isParad(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//是否平行 if((y2-y1)*(x4-x3)==(y4-y3)*(x2-x1)){ return true; } return false; } int numParad(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//平行边的组数 int cnt=0; if(isParad(x1,y1,x2,y2,x2,y2,x3,y3))cnt++; if(isParad(x2,y2,x3,y3,x3,y3,x4,y4))cnt++; if(isParad(x3,y3,x4,y4,x4,y4,x5,y5))cnt++; if(isParad(x4,y4,x5,y5,x5,y5,x1,y1))cnt++; if(isParad(x5,y5,x1,y1,x1,y1,x2,y2))cnt++; return cnt; } boolean pointCoincide(double x1,double y1,double x2,double y2){//两点是否重合 if(x1-x2==0&&y1-y2==0){ return true; } return false; } int isPointCoincide(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//重点组数 int cnt=0; if(pointCoincide(x1,y1,x2,y2))cnt++; if(pointCoincide(x1,y1,x3,y3))cnt++; if(pointCoincide(x1,y1,x4,y4))cnt++; if(pointCoincide(x1,y1,x5,y5))cnt++; if(pointCoincide(x2,y2,x3,y3))cnt++; if(pointCoincide(x2,y2,x4,y4))cnt++; if(pointCoincide(x2,y2,x5,y5))cnt++; if(pointCoincide(x3,y3,x4,y4))cnt++; if(pointCoincide(x3,y3,x5,y5))cnt++; if(pointCoincide(x4,y4,x5,y5))cnt++; return cnt; } int loc(double x1,double y1,double x2,double y2,double x3,double y3){//点与线的位置关系 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; if(Math.abs(A12*x3+B12*y3+C12)<0.0000001){ return 0; } else if(A12*x3+B12*y3+C12<0){ return -1; } else{ return 1; } } boolean lineCoincide(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//两线是否重合 if(isParad(x1, y1, x2, y2, x3, y3, x4, y4)){ if(loc(x1, y1, x2, y2, x3, y3)==0&&loc(x1, y1, x2, y2, x4, y4)==0&&!pointCoincide(x3,y3,x4,y4)&&!pointCoincide(x1,y1,x2,y2)){ return true; } } return false; } double pointDis(double x1,double y1,double x2,double y2,double x3,double y3){//点线距离 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double D=Math.sqrt(A12*A12+B12*B12); double res=(A12*x3+B12*y3+C12)/D; return res; } } class Trangle{//三角形类 void sTrangle(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//求并输出面积 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A13=y1-y3; double B13=x3-x1; double C13=x1*y3-x3*y1; double A45=y4-y5; double B45=x5-x4; double C45=x4*y5-x5*y4; double D12_45=A12*B45-A45*B12; double D13_45=A13*B45-A45*B12; double X12_45=(B12*C45-B45*C12)/D12_45; double Y12_45=(A45*C12-A12*C45)/D12_45; double X13_45=(B13*C45-B45*C13)/D13_45; double Y13_45=(A45*C13-A13*C45)/D13_45; double L14=Math.sqrt((X12_45-x1)*(X12_45-x1)+(Y12_45-y1)*(Y12_45-y1)); double L15=Math.sqrt((X13_45-x1)*(X13_45-x1)+(Y13_45-y1)*(Y13_45-y1)); double L12=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); double L13=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); double f=L14*L15/(L12*L13); double S=qinjiushao(x1, y1, x2, y2, x3, y3); double rmin=Math.min(S*f,S-S*f); double rmax=Math.max(S*f,S-S*f); BigDecimal smn=new BigDecimal(rmin); BigDecimal smx=new BigDecimal(rmax); rmin=smn.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); rmax=smx.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 "+rmin+" "+rmax); } double qinjiushao(double x1,double y1,double x2,double y2,double x3,double y3){//求面积 double a=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); double b=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); double c=Math.sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3)); double p=(a+b+c)/2; double s=Math.sqrt(p*(p-a)*(p-b)*(p-c)); return s; } } class Quadrilateral{//四边形类 void getQua(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x6,double y6,double x7,double y7){//得到距离 Line line = new Line(); double[] X = new double[4]; double[] Y = new double[4]; double[] dis = new double[4]; double[] Dis = new double[4]; int[] loc = new int[4]; int[] pre = new int[4]; boolean[] used = new boolean[4]; dis[0] = line.pointDis(x6, y6, x7, y7, x1, y1); Dis[0] = line.pointDis(x6, y6, x7, y7, x1, y1); X[0] = x1; Y[0] = y1; dis[1] = line.pointDis(x6, y6, x7, y7, x2, y2); Dis[1] = line.pointDis(x6, y6, x7, y7, x2, y2); X[1] = x2; Y[1] = y2; dis[2] = line.pointDis(x6, y6, x7, y7, x3, y3); Dis[2] = line.pointDis(x6, y6, x7, y7, x3, y3); X[2] = x3; Y[2] = y3; dis[3] = line.pointDis(x6, y6, x7, y7, x4, y4); Dis[3] = line.pointDis(x6, y6, x7, y7, x4, y4); X[3] = x4; Y[3] = y4; Arrays.sort(dis); for (int i = 0; i < 4; i++) { loc[i] = 0; used[i]=false; } for (int i = 0; i < 4; i++) { for (int j = 0; j < 4; j++) { if(Dis[i] == dis[j] && !used[j]){ used[j]=true; loc[i]=j; pre[j]=i; break; } } } if(line.pointCoincide(X[pre[0]],Y[pre[0]],x1,y1)){ if(line.loc(x6,y6,x7,y7,x1,y1)*line.loc(x6,y6,x7,y7,x2,y2)>0){ getS(x1,y1,x4,y4,x3,y3,x2,y2,x6,y6,x7,y7); } else{ getS(x1,y1,x2,y2,x3,y3,x4,y4,x6,y6,x7,y7); } } else if(line.pointCoincide(X[pre[0]],Y[pre[0]],x2,y2)){ if(line.loc(x6,y6,x7,y7,x2,y2)*line.loc(x6,y6,x7,y7,x3,y3)>0) { getS(x2, y2, x1, y1, x4, y4,x3, y3, x6, y6, x7, y7); } else{ getS(x2, y2, x3, y3, x4, y4, x1, y1, x6, y6, x7, y7); } } else if(line.pointCoincide(X[pre[0]],Y[pre[0]],x3,y3)){ if(line.loc(x6,y6,x7,y7,x3,y3)*line.loc(x6,y6,x7,y7,x4,y4)>0) { getS(x3, y3, x2, y2, x1, y1, x4, y4, x6, y6, x7, y7); } else{ getS(x3, y3, x4, y4, x1, y1, x2, y2, x6, y6, x7, y7); } } else{ if(line.loc(x6,y6,x7,y7,x3,y3)*line.loc(x6,y6,x7,y7,x4,y4)>0) { getS(x4, y4, x1, y1, x2, y2, x3, y3, x6, y6, x7, y7); } else{ getS(x4, y4, x3, y3, x2, y2, x1, y1, x6, y6, x7, y7); } } } void getS(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5,double x6,double y6){//求面积并输出 Trangle trangle=new Trangle(); double S=trangle.qinjiushao(x1, y1, x2, y2, x4, y4)+trangle.qinjiushao(x2, y2, x3, y3, x4, y4); Line line=new Line(); int loc1=line.loc(x5, y5, x6, y6, x1, y1); int loc2=line.loc(x5, y5, x6, y6, x2, y2); int loc3=line.loc(x5, y5, x6, y6, x3, y3); int loc4=line.loc(x5, y5, x6, y6, x4, y4); double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A14=y1-y4; double B14=x4-x1; double C14=x1*y4-x4*y1; double A23=y2-y3; double B23=x3-x2; double C23=x2*y3-x3*y2; double A34=y3-y4; double B34=x4-x3; double C34=x3*y4-x4*y3; double A56=y5-y6; double B56=x6-x5; double C56=x5*y6-x6*y5; double D56_12=A56*B12-A12*B56; double D56_14=A56*B14-A14*B56; double D56_23=A56*B23-A23*B56; double D56_34=A56*B34-A34*B56; double sl=0,sr=0; if((loc2<=0&&loc3>0&&loc4<=0)||(loc2>=0&&loc3<0&&loc4>=0)){ double X56_23=(B56*C23-B23*C56)/D56_23; double Y56_23=(A23*C56-A56*C23)/D56_23; double X56_34=(B56*C34-B34*C56)/D56_34; double Y56_34=(A34*C56-A56*C34)/D56_34; sl=trangle.qinjiushao(x3,y3,X56_23,Y56_23,X56_34,Y56_34); sr=S-sl; } else if((loc2<0&&loc3>=0)||(loc2>0&&loc3<=0)){ double X56_12=(B56*C12-B12*C56)/D56_12; double Y56_12=(A12*C56-A56*C12)/D56_12; double X56_23=(B56*C23-B23*C56)/D56_23; double Y56_23=(A23*C56-A56*C23)/D56_23; sl= trangle.qinjiushao(x2,y2,X56_12,Y56_12,X56_23,Y56_23); sr=S-sl; } else if((loc1<0&&loc2>0&&loc4<0&&loc3>0)||(loc1>0&&loc2<0&&loc3<0&&loc4>0)){ double X56_12=(B56*C12-B12*C56)/D56_12; double Y56_12=(A12*C56-A56*C12)/D56_12; double X56_34=(B56*C34-B34*C56)/D56_34; double Y56_34=(A34*C56-A56*C34)/D56_34; sl= trangle.qinjiushao(x2,y2,X56_12,Y56_12,X56_34,Y56_34)+ trangle.qinjiushao(x2,y2,x3,y3,X56_34,Y56_34); sr=S-sl; } else{ double X56_14=(B56*C14-B14*C56)/D56_14; double Y56_14=(A14*C56-A56*C14)/D56_14; double X56_12=(B56*C12-B12*C56)/D56_12; double Y56_12=(A12*C56-A56*C12)/D56_12; sl= trangle.qinjiushao(x1,y1,X56_12,Y56_12,X56_14,Y56_14); sr=S-sl; } double rmin=Math.min(sl,sr); double rmax=Math.max(sl,sr); BigDecimal smn = new BigDecimal(rmin); BigDecimal smx = new BigDecimal(rmax); rmin = smn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = smx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } } class Pentagon {//五边形类 void getPen(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5,double x6,double y6,double x7,double y7){//求点距,同四边形 Line line = new Line(); double[] X = new double[5]; double[] Y = new double[5]; double[] dis = new double[5]; double[] Dis = new double[5]; int[] loc = new int[5]; int[] pre = new int[5]; boolean[] used = new boolean[5]; dis[0] = line.pointDis(x6, y6, x7, y7, x1, y1); Dis[0] = line.pointDis(x6, y6, x7, y7, x1, y1); X[0] = x1; Y[0] = y1; dis[1] = line.pointDis(x6, y6, x7, y7, x2, y2); Dis[1] = line.pointDis(x6, y6, x7, y7, x2, y2); X[1] = x2; Y[1] = y2; dis[2] = line.pointDis(x6, y6, x7, y7, x3, y3); Dis[2] = line.pointDis(x6, y6, x7, y7, x3, y3); X[2] = x3; Y[2] = y3; dis[3] = line.pointDis(x6, y6, x7, y7, x4, y4); Dis[3] = line.pointDis(x6, y6, x7, y7, x4, y4); X[3] = x4; Y[3] = y4; dis[4] = line.pointDis(x6, y6, x7, y7, x5, y5); Dis[4] = line.pointDis(x6, y6, x7, y7, x5, y5); X[4] = x5; Y[4] = y5; Arrays.sort(dis); for (int i = 0; i < 5; i++) { loc[i] = 0; used[i]=false; } for (int i = 0; i < 5; i++) { for (int j = 0; j < 5; j++) { if(Dis[i] == dis[j] && !used[j]){ used[j] = true; loc[i] = j; pre[j] = i; break; } } } if(line.pointCoincide(X[pre[0]],Y[pre[0]],x1,y1)){ getS(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7); } else if(line.pointCoincide(X[pre[0]],Y[pre[0]],x2,y2)){ getS(x2,y2,x3,y3,x4,y4,x5,y5,x1,y1,x6,y6,x7,y7); } else if(line.pointCoincide(X[pre[0]],Y[pre[0]],x3,y3)){ getS(x3,y3,x4,y4,x5,y5,x1,y1,x2,y2,x6,y6,x7,y7); } else if(line.pointCoincide(X[pre[0]],Y[pre[0]],x3,y3)){ getS(x4,y4,x5,y5,x1,y1,x2,y2,x3,y3,x6,y6,x7,y7); } else{ getS(x5,y5,x1,y1,x2,y2,x3,y3,x4,y4,x6,y6,x7,y7); } } void getS(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4, double x5, double y5, double x6, double y6,double x7,double y7) {//求面积并输出 Line line = new Line(); Trangle trangle = new Trangle(); double S=trangle.qinjiushao(x1, y1, x2, y2, x3, y3) + trangle.qinjiushao(x1, y1, x3, y3, x4, y4) + trangle.qinjiushao(x1,y1,x4,y4,x5,y5); int loc1=line.loc(x6,y6,x7,y7,x1,y1); int loc2=line.loc(x6,y6,x7,y7,x2,y2); int loc3=line.loc(x6,y6,x7,y7,x3,y3); int loc4=line.loc(x6,y6,x7,y7,x4,y4); int loc5=line.loc(x6,y6,x7,y7,x5,y5); double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A45=y4-y5; double B45=x5-x4; double C45=x4*y5-x5*y4; double A23=y2-y3; double B23=x3-x2; double C23=x2*y3-x3*y2; double A34=y3-y4; double B34=x4-x3; double C34=x3*y4-x4*y3; double A15=y1-y5; double B15=x5-x1; double C15=x1*y5-x5*y1; double A67=y6-y7; double B67=x7-x6; double C67=x6*y7-x7*y6; double D67_12=A67*B12-A12*B67; double D67_23=A67*B23-A23*B67; double D67_34=A67*B34-A34*B67; double D67_45=A67*B45-A45*B67; double D67_15=A67*B15-A15*B67; double sl=0,sr=0; if((loc3<0&&loc4>=0&&loc2>=0)||(loc3>0&&loc4<=0&&loc2<=0)){ double X67_23=(B67*C23-B23*C67)/D67_23; double Y67_23=(A23*C67-A67*C23)/D67_23; double X67_34=(B67*C34-B34*C67)/D67_34; double Y67_34=(A34*B67-A67*B34)/D67_34; sl= trangle.qinjiushao(x3,y3,X67_23,Y67_23,X67_34,Y67_34); sr=S-sl; } else if((loc4<0&&loc3>=0&&loc5>=0)||(loc4>0&&loc3<=0&&loc5<=0)){ double X67_34=(B67*C34-B34*C67)/D67_34; double Y67_34=(A34*B67-A67*B34)/D67_34; double X67_45=(B67*C45-B45*C67)/D67_45; double Y67_45=(A45*C67-A67*C45)/D67_45; sl= trangle.qinjiushao(x4,y4,X67_34,Y67_34,X67_45,Y67_45); sr=S-sl; } else if((loc3<0&&loc4<0&&loc2>=0&&loc5>=0)||(loc3>0&&loc4>0&&loc5<=0&&loc2<=0)){ double X67_23=(B67*C23-B23*C67)/D67_23; double Y67_23=(A23*C67-A67*C23)/D67_23; double X67_45=(B67*C45-B45*C67)/D67_45; double Y67_45=(A45*C67-A67*C45)/D67_45; sl= trangle.qinjiushao(x3,y3,x4,y4,X67_23,Y67_23)+ trangle.qinjiushao(x4,y4,X67_23,Y67_23,X67_45,Y67_45); sr=S-sl; } else if((loc2<0&&loc4<0&&loc5>=0)||(loc2>0&&loc4>0&&loc5<=0)){ double X67_45=(B67*C45-B45*C67)/D67_45; double Y67_45=(A45*C67-A67*C45)/D67_45; double X67_12=(B67*C12-B12*C67)/D67_12; double Y67_12=(A12*C67-A67*C12)/D67_12; sl= trangle.qinjiushao(x1,y1,x5,y5,X67_12,Y67_12)+ trangle.qinjiushao(x5,y5,X67_12,Y67_12,X67_45,Y67_45); sr=S-sl; } else if((loc5<=0&&loc2>0)||(loc5>=0&&loc2<0)){ double X67_23=(B67*C23-B23*C67)/D67_23; double Y67_23=(A23*C67-A67*C23)/D67_23; double X67_15=(B67*C15-B15*C67)/D67_15; double Y67_15=(A15*C67-A67*C15)/D67_15; sl= trangle.qinjiushao(x1,y1,x2,y2,X67_15,Y67_15)+ trangle.qinjiushao(x2,y2,X67_15,Y67_15,X67_23,Y67_23); sr=S-sl; } else{ double X67_12=(B67*C12-B12*C67)/D67_12; double Y67_12=(A12*C67-A67*C12)/D67_12; double X67_15=(B67*C15-B15*C67)/D67_15; double Y67_15=(A15*C67-A67*C15)/D67_15; sl= trangle.qinjiushao(X67_12,Y67_12,X67_15,Y67_15,x1,y1); sr=S-sl; } double rmin=Math.min(sl,sr); double rmax=Math.max(sl,sr); BigDecimal smn = new BigDecimal(rmin); BigDecimal smx = new BigDecimal(rmax); rmin = smn.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); rmax = smx.setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println("2 " + rmin + " " + rmax); } boolean isTPentagon(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4, double x5, double y5) {//判断是否为凹五边形 Trangle trangle = new Trangle(); double S = trangle.qinjiushao(x1, y1, x2, y2, x3, y3) + trangle.qinjiushao(x1, y1, x4, y4, x3, y3); double SS = trangle.qinjiushao(x1, y1, x2, y2, x5, y5) + trangle.qinjiushao(x5, y5, x2, y2, x3, y3) + trangle.qinjiushao(x4, y4, x5, y5, x3, y3) + trangle.qinjiushao(x1, y1, x4, y4, x5, y5); if (Math.abs(S - SS) < 0.0000001 || S - SS > 0) { return false; } return true; } }
上sourcemonitor分析!
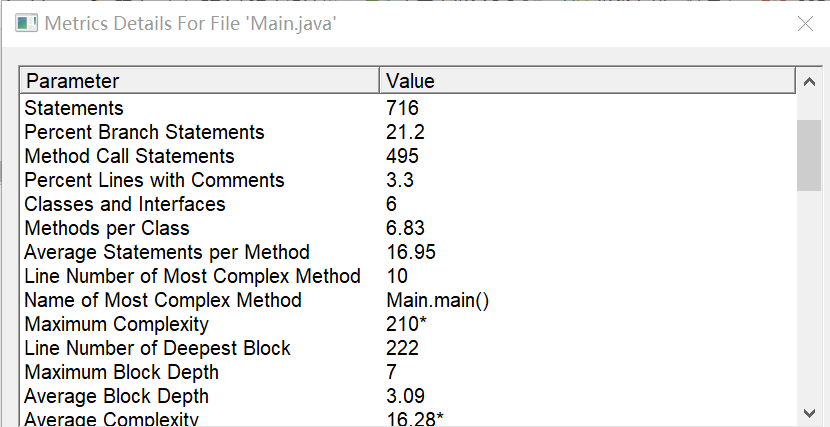

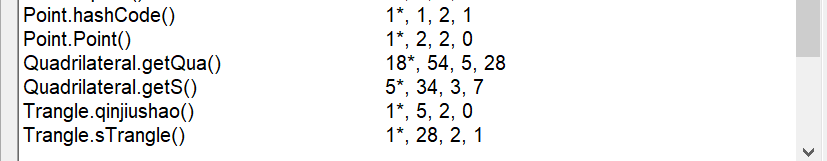
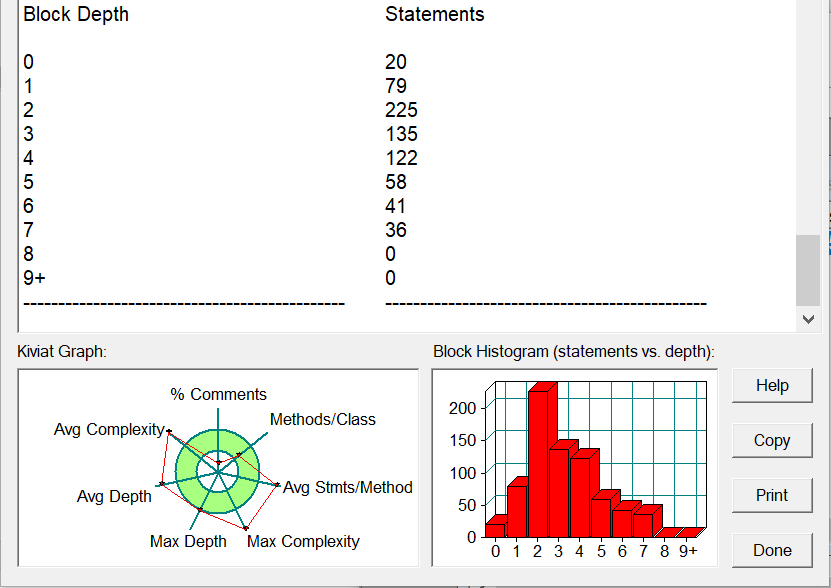
由sourcemonitor分析得,相比没有用类,代码平均深度、最大深度显著降低,同时代码可读性提高。代码的平均复杂度仍处于高位,代码结构可进一步优化。
总结:一道非常考验人劝退的题,但用上类的方法以后,思路清晰了不少,也避免了功能相似的代码的冗余,成功压缩代码行数。
第五次大作业T2
题面:
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例:
在这里给出一组输入。例如:
4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6输出样例:
在这里给出相应的输出。例如:
the previous pentagon coincides with the following pentagon本次作业最难的题来了!来看看最难的case5吧!
case5:
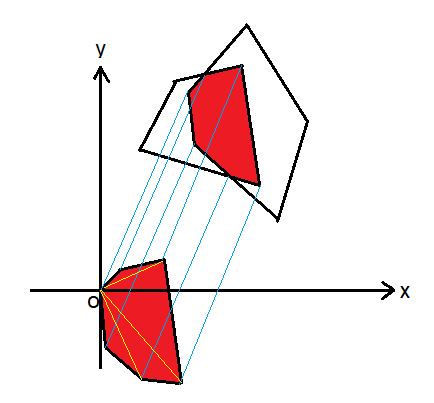
依次找出两多边形的交点、一个多边形在另一个多边形内或边上的顶点,任选一点移至坐标原点((x0,y0)->(0,0)),其它点同时做相应改变((x,y)->(x-x0,y-y0))。用atan2(y,x)函数可得每个点的弧度值,再排序,最后依次求构成三角形的面积并相加得到答案。
我滴代码
import java.math.BigDecimal; import java.util.*; import java.lang.*; public class Main{ Point t; public static void main(String[] args){ double x1=0,y1=0,x2=0,y2=0,x3=0,y3=0,x4=0,y4=0,x5=0,y5=0,x6=0,y6=0,x7=0,y7=0,x8=0,y8=0,x9=0,y9=0,x10=0,y10=0; Scanner bjsn=new Scanner(System.in); String s=bjsn.nextLine(); int len=s.length(); int cnt=0; //基本格式判断 for(int i=0;i<len;i++){ if(s.charAt(i)==','){ cnt++; } } if(cnt==0){ System.out.println("Wrong Format"); return; } if(s.charAt(0)<'4'||s.charAt(0)>'6'||s.charAt(1)!=':'||(s.charAt(len-1)<'0'||s.charAt(len-1)>'9')){ System.out.println("Wrong Format"); return; } int pos=2; if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){ System.out.println("Wrong Format"); return; } String sss=s.substring(2,len); String ss[]=sss.split(" "); String str[]=null; for(String Str:ss){//正则输入法判断格式并提取数字 str=Str.split(","); for(String tt:str){ if(!tt.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){ System.out.println("Wrong Format"); return; } } } Line line = new Line(); Triangle triangle = new Triangle(); Quadrilateral quadrilateral = new Quadrilateral(); Pentagon pentagon = new Pentagon(); switch (s.charAt(0)){ case '4'://位置关系判断 if(ss.length!=10) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str=ss[0].split(",");x1=Double.parseDouble(str[0]);y1=Double.parseDouble(str[1]); str=ss[1].split(",");x2=Double.parseDouble(str[0]);y2=Double.parseDouble(str[1]); str=ss[2].split(",");x3=Double.parseDouble(str[0]);y3=Double.parseDouble(str[1]); str=ss[3].split(",");x4=Double.parseDouble(str[0]);y4=Double.parseDouble(str[1]); str=ss[4].split(",");x5=Double.parseDouble(str[0]);y5=Double.parseDouble(str[1]); str=ss[5].split(",");x6=Double.parseDouble(str[0]);y6=Double.parseDouble(str[1]); str=ss[6].split(",");x7=Double.parseDouble(str[0]);y7=Double.parseDouble(str[1]); str=ss[7].split(",");x8=Double.parseDouble(str[0]);y8=Double.parseDouble(str[1]); str=ss[8].split(",");x9=Double.parseDouble(str[0]);y9=Double.parseDouble(str[1]); str=ss[9].split(",");x10=Double.parseDouble(str[0]);y10=Double.parseDouble(str[1]); Point[] res1 = xingzhuang(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5); Point[] res2 = xingzhuang(x6,y6,x7,y7,x8,y8,x9,y9,x10,y10); int ans1=0,tot1=0,ans2=0,tot2=0,lco=0,cco=0,pco=0; for(int i=0;i< res1.length;i++){ for(int j=0;j< res2.length;j++){ if(line.lineCoincide(res1[i].x,res1[i].y,res1[(i+1)% res1.length].x,res1[(i+1)% res1.length].y,res2[j].x,res2[j].y,res2[(j+1)% res2.length].x,res2[(j+1)% res2.length].y)){ lco++; } if(line.cross1(res1[i].x,res1[i].y,res1[(i+1)% res1.length].x,res1[(i+1)% res1.length].y,res2[j].x,res2[j].y,res2[(j+1)% res2.length].x,res2[(j+1)% res2.length].y)){ cco++; } if(line.pointCoincide(res1[i].x,res1[i].y,res2[j].x,res2[j].y)){ pco++; } } } if(res1.length==3&&res2.length==3){//(3,3),(3,4),(3,5),(4,3),(4,4),(4,5),(5,3),(5,4),(5,5)9种情况遍历 for(int i = 0; i <= 2; i++){ if(triangle.inTriangle(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res1[i].x,res1[i].y)>0)ans1++; else if(triangle.inTriangle(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 2; i++){ if(triangle.inTriangle(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res2[i].x,res2[i].y)>0)ans2++; else if(triangle.inTriangle(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==3&&tot2==3)System.out.println("the previous triangle coincides with the following triangle"); else if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco>0)System.out.println("the previous triangle is connected to the following triangle");else if(cco>0)System.out.println("the previous triangle is interlaced with the following triangle");else System.out.println("no overlapping area between the previous triangle and the following triangle");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==3&&tot2==0)System.out.println("the previous triangle is inside the following triangle");else if(tot1==0&&tot2==3)System.out.println("the previous triangle contains the following triangle");else if(cco>0)System.out.println("the previous triangle is interlaced with the following triangle");else System.out.println("the previous triangle is connected to the following triangle");} else if(ans1+tot1==3){System.out.println("the previous triangle is inside the following triangle");} else if(ans2+tot2==3){System.out.println("the previous triangle contains the following triangle");} else {System.out.println("the previous triangle is interlaced with the following triangle");} } else if(res1.length==3&&res2.length==4){ for(int i = 0; i <= 2; i++){ if(quadrilateral.inQuarilateral(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res1[i].x,res1[i].y)>0)ans1++; else if(quadrilateral.inQuarilateral(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 3; i++){ if(triangle.inTriangle(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res2[i].x,res2[i].y)>0)ans2++; else if(triangle.inTriangle(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res2[i].x,res2[i].y)==0)tot2++; } if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco==0)System.out.println("the previous triangle is connected to the following quadrilateral");else if(cco>0){System.out.println("the previous triangle is interlaced with the following quadrilateral");}else System.out.println("no overlapping area between the previous triangle and the following quadrilateral");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==3&&tot2==0)System.out.println("the previous triangle is inside the following quadrilateral");else if(tot1==0&&tot2==4)System.out.println("the previous triangle contains the following quadrilateral");else if(cco>0)System.out.println("the previous triangle is interlaced with the following quadrilateral");else if(pco==3)System.out.println("the previous triangle is inside the following quadrilateral");else System.out.println("the previous triangle is connected to the following quadrilateral");} else if(ans1+tot1==3){System.out.println("the previous triangle is inside the following quadrilateral");} else if(ans2+tot2==4){System.out.println("the previous triangle contains the following quadrilateral");} else {System.out.println("the previous triangle is interlaced with the following quadrilateral");} } else if(res1.length==3&&res2.length==5){ for(int i = 0; i <= 2; i++){ if(pentagon.inPentagon(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res2[4].x,res2[4].y,res1[i].x,res1[i].y)>0)ans1++; else if(pentagon.inPentagon(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res2[4].x,res2[4].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 4; i++){ if(triangle.inTriangle(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res2[i].x,res2[i].y)>0)ans2++; else if(triangle.inTriangle(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res2[i].x,res2[i].y)==0)tot2++; } if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco==0)System.out.println("the previous triangle is connected to the following pentagon");else if(cco>0){System.out.println("the previous triangle is interlaced with the following pentagon");}else System.out.println("no overlapping area between the previous triangle and the following pentagon");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==3&&tot2==0)System.out.println("the previous triangle is inside the following pentagon");else if(tot1==0&&tot2==5)System.out.println("the previous triangle contains the following pentagon");else if(cco>0)System.out.println("the previous triangle is interlaced with the following pentagon");else if(pco==3)System.out.println("the previous triangle is inside the following pentagon");else System.out.println("the previous triangle is connected to the following pentagon");} else if(ans1+tot1==3){System.out.println("the previous triangle is inside the following pentagon");} else if(ans2+tot2==5){System.out.println("the previous triangle contains the following pentagon");} else {System.out.println("the previous triangle is interlaced with the following pentagon");} } else if(res1.length==4&&res2.length==3){ for(int i = 0; i <= 3; i++){ if(triangle.inTriangle(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res1[i].x,res1[i].y)>0)ans1++; else if(triangle.inTriangle(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 2; i++){ if(quadrilateral.inQuarilateral(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res2[i].x,res2[i].y)>0)ans2++; else if(quadrilateral.inQuarilateral(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==4&&tot2==3)System.out.println("the previous quadrilateral coincides with the following triangle"); else if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco>0)System.out.println("the previous quadrilateral is connected to the following triangle");else if(cco>0)System.out.println("the previous quadrilateral is interlaced with the following triangle");else System.out.println("no overlapping area between the previous quadrilateral and the following triangle");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==4&&tot2==0)System.out.println("the previous quadrilateral is inside the following triangle");else if(tot1==0&&tot2==3)System.out.println("the previous quadrilateral contains the following triangle");else if(cco>0)System.out.println("the previous quadrilateral is interlaced with the following triangle");else if(pco==3)System.out.println("the previous quadrilateral contains the following triangle");else System.out.println("the previous quadrilateral is connected to the following triangle");} else if(ans1+tot1==4){System.out.println("the previous quadrilateral is inside the following triangle");} else if(ans2+tot2==3){System.out.println("the previous quadrilateral contains the following triangle");} else {System.out.println("the previous quadrilateral is interlaced with the following triangle");} } else if(res1.length==4&&res2.length==4){ for(int i = 0; i <= 3; i++){ if(quadrilateral.inQuarilateral(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res1[i].x,res1[i].y)>0)ans1++; else if(quadrilateral.inQuarilateral(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 3; i++){ if(quadrilateral.inQuarilateral(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res2[i].x,res2[i].y)>0)ans2++; else if(quadrilateral.inQuarilateral(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==4&&tot2==4)System.out.println("the previous quadrilateral coincides with the following quadrilateral"); else if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco>0)System.out.println("the previous quadrilateral is connected to the following quadrilateral");else if(cco>0)System.out.println("the previous quadrilateral is interlaced with the following quadrilateral");else System.out.println("no overlapping area between the previous quadrilateral and the following quadrilateral");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==4&&tot2==0)System.out.println("the previous quadrilateral is inside the following quadrilateral");else if(tot1==0&&tot2==4)System.out.println("the previous quadrilateral contains the following quadrilateral");else if(cco>0)System.out.println("the previous quadrilateral is interlaced with the following quadrilateral");else System.out.println("the previous quadrilateral is connected to the following quadrilateral");} else if(ans1+tot1==4){System.out.println("the previous quadrilateral is inside the following quadrilateral");} else if(ans2+tot2==4){System.out.println("the previous quadrilateral contains the following quadrilateral");} else {System.out.println("the previous quadrilateral is interlaced with the following quadrilateral");} } else if(res1.length==4&&res2.length==5){ for(int i = 0; i <= 3; i++){ if(pentagon.inPentagon(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res2[4].x,res2[4].y,res1[i].x,res1[i].y)>0)ans1++; else if(pentagon.inPentagon(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res2[4].x,res2[4].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 4; i++){ if(quadrilateral.inQuarilateral(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res2[i].x,res2[i].y)>0)ans2++; else if(quadrilateral.inQuarilateral(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==4&&tot2==5)System.out.println("the previous quadrilateral is interlaced with the following pentagon"); else if((tot1==4&&tot2==4&&ans1==0&&ans2==0)||(tot1+ans1==4&&ans2==0)){System.out.println("the previous quadrilateral is inside the following pentagon");} else if(ans2+tot2==5&&ans1==0){System.out.println("the previous quadrilateral contains the following pentagon");} else if((pco==1&&ans1==0&&ans2==0&&tot1==1&&tot2==1)||(lco==1&&ans1==0&&ans2==0)){System.out.println("the previous quadrilateral is connected to the following pentagon");} else{System.out.println("the previous quadrilateral is interlaced with the following pentagon");} } else if(res1.length==5&&res2.length==3){ for(int i = 0; i <= 4; i++){ if(triangle.inTriangle(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res1[i].x,res1[i].y)>0)ans1++; else if(triangle.inTriangle(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 2; i++){ if(pentagon.inPentagon(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res1[4].x,res1[4].y,res2[i].x,res2[i].y)>0)ans2++; else if(pentagon.inPentagon(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res1[4].x,res1[4].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==5&&tot2==3)System.out.println("the previous pentagon coincides with the following triangle"); else if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco>0)System.out.println("the previous pentagon is connected to the following triangle");else if(cco>0)System.out.println("the previous pentagon is interlaced with the following triangle");else System.out.println("no overlapping area between the previous pentagon and the following triangle");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==5&&tot2==0)System.out.println("the previous pentagon is inside the following triangle");else if(tot1==0&&tot2==3)System.out.println("the previous pentagon contains the following triangle");else if(cco>0)System.out.println("the previous pentagon is interlaced with the following triangle");else if(pco==3)System.out.println("the previous pentagon contains the following triangle");else System.out.println("the previous pentagon is connected to the following triangle");} else if(ans1+tot1==5){System.out.println("the previous pentagon is inside the following triangle");} else if(ans2+tot2==3){System.out.println("the previous pentagon contains the following triangle");} else {System.out.println("the previous pentagon is interlaced with the following triangle");} } else if(res1.length==5&&res2.length==4){ for(int i = 0; i <= 4; i++){ if(quadrilateral.inQuarilateral(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res1[i].x,res1[i].y)>0)ans1++; else if(quadrilateral.inQuarilateral(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 3; i++){ if(pentagon.inPentagon(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res1[4].x,res1[4].y,res2[i].x,res2[i].y)>0)ans2++; else if(pentagon.inPentagon(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res1[4].x,res1[4].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==5&&tot2==4)System.out.println("the previous pentagon coincides with the following quadrilateral"); else if(ans1==0&&ans2==0&&tot1==0&&tot2==0){if(lco>0&&cco>0)System.out.println("the previous pentagon is connected to the following quadrilateral");else if(cco>0)System.out.println("the previous pentagon is interlaced with the following quadrilateral");else System.out.println("no overlapping area between the previous pentagon and the following quadrilateral");} else if((tot1>0||tot2>0)&&ans1==0&&ans2==0){if(tot1==5&&tot2==0)System.out.println("the previous pentagon is inside the following quadrilateral");else if(tot1==0&&tot2==4)System.out.println("the previous pentagon contains the following quadrilateral");else if(cco>0)System.out.println("the previous pentagon is interlaced with the following quadrilateral");else if(pco==4)System.out.println("the previous pentagon contains the following quadrilateral");else System.out.println("the previous pentagon is connected to the following quadrilateral");} else if(ans1+tot1==5){System.out.println("the previous pentagon is inside the following quadrilateral");} else if(ans2+tot2==4){System.out.println("the previous pentagon contains the following quadrilateral");} else {System.out.println("the previous pentagon is interlaced with the following quadrilateral");} } else{ for(int i = 0; i <= 4; i++){ if(pentagon.inPentagon(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res2[4].x,res2[4].y,res1[i].x,res1[i].y)>0)ans1++; else if(pentagon.inPentagon(res2[0].x,res2[0].y,res2[1].x,res2[1].y,res2[2].x,res2[2].y,res2[3].x,res2[3].y,res2[4].x,res2[4].y,res1[i].x,res1[i].y)==0)tot1++; } for(int i = 0; i <= 4; i++){ if(pentagon.inPentagon(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res1[4].x,res1[4].y,res2[i].x,res2[i].y)>0)ans2++; else if(pentagon.inPentagon(res1[0].x,res1[0].y,res1[1].x,res1[1].y,res1[2].x,res1[2].y,res1[3].x,res1[3].y,res1[4].x,res1[4].y,res2[i].x,res2[i].y)==0)tot2++; } if(tot1==5&&tot2==5)System.out.println("the previous pentagon coincides with the following pentagon"); else System.out.println("the previous pentagon is connected to the following pentagon"); } break; case '5': if(ss.length!=10) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str=ss[0].split(",");x1=Double.parseDouble(str[0]);y1=Double.parseDouble(str[1]); str=ss[1].split(",");x2=Double.parseDouble(str[0]);y2=Double.parseDouble(str[1]); str=ss[2].split(",");x3=Double.parseDouble(str[0]);y3=Double.parseDouble(str[1]); str=ss[3].split(",");x4=Double.parseDouble(str[0]);y4=Double.parseDouble(str[1]); str=ss[4].split(",");x5=Double.parseDouble(str[0]);y5=Double.parseDouble(str[1]); str=ss[5].split(",");x6=Double.parseDouble(str[0]);y6=Double.parseDouble(str[1]); str=ss[6].split(",");x7=Double.parseDouble(str[0]);y7=Double.parseDouble(str[1]); str=ss[7].split(",");x8=Double.parseDouble(str[0]);y8=Double.parseDouble(str[1]); str=ss[8].split(",");x9=Double.parseDouble(str[0]);y9=Double.parseDouble(str[1]); str=ss[9].split(",");x10=Double.parseDouble(str[0]);y10=Double.parseDouble(str[1]); int kk=0; Point[] pol1 = xingzhuang(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5); Point[] pol2 = xingzhuang(x6,y6,x7,y7,x8,y8,x9,y9,x10,y10); LinkedHashSet<Point>cover = new LinkedHashSet<>(); for(int i = 0; i < pol1.length ;i++){ for(int j = 0; j < pol2.length ;j++){ if(line.cross(pol1[i].x,pol1[i].y,pol1[(i+1)%pol1.length].x,pol1[(i+1)% pol1.length].y,pol2[j].x,pol2[j].y,pol2[(j+1)%pol2.length].x,pol2[(j+1)% pol2.length].y)){ cover.add(line.tlpoint(pol1[i].x,pol1[i].y,pol1[(i+1)%pol1.length].x,pol1[(i+1)% pol1.length].y,pol2[j].x,pol2[j].y,pol2[(j+1)%pol2.length].x,pol2[(j+1)% pol2.length].y)); } if(line.pointCoincide(pol1[i].x,pol1[i].y,pol2[j].x,pol2[j].y)){ cover.add(new Point(pol1[i].x,pol1[i].y)); } if(pol1.length==3){ if(triangle.inTriangle(pol1[0].x,pol1[0].y,pol1[1].x,pol1[1].y,pol1[2].x,pol1[2].y,pol2[j].x,pol2[j].y)==1){ cover.add(new Point(pol2[j].x,pol2[j].y)); } } else if(pol1.length==4){ if(quadrilateral.inQuarilateral(pol1[0].x,pol1[0].y,pol1[1].x,pol1[1].y,pol1[2].x,pol1[2].y,pol1[3].x,pol1[3].y,pol2[j].x,pol2[j].y)==1){ cover.add(new Point(pol2[j].x,pol2[j].y)); } } else if(pol1.length==5){ if(pentagon.inPentagon(pol1[0].x,pol1[0].y,pol1[1].x,pol1[1].y,pol1[2].x,pol1[2].y,pol1[3].x,pol1[3].y,pol1[4].x,pol1[4].y,pol2[j].x,pol2[j].y)==1){ cover.add(new Point(pol2[j].x,pol2[j].y)); } } if(pol2.length==3){ if(triangle.inTriangle(pol2[0].x,pol2[0].y,pol2[1].x,pol2[1].y,pol2[2].x,pol2[2].y,pol1[i].x,pol1[i].y)==1){ cover.add(new Point(pol1[i].x,pol1[i].y)); } } else if(pol2.length==4){ if(quadrilateral.inQuarilateral(pol2[0].x,pol2[0].y,pol2[1].x,pol2[1].y,pol2[2].x,pol2[2].y,pol2[3].x,pol2[3].y,pol1[i].x,pol1[i].y)==1){ cover.add(new Point(pol1[i].x,pol1[i].y)); } } else if(pol2.length==5){ if(pentagon.inPentagon(pol2[0].x,pol2[0].y,pol2[1].x,pol2[1].y,pol2[2].x,pol2[2].y,pol2[3].x,pol2[3].y,pol2[4].x,pol2[4].y,pol1[i].x,pol1[i].y)==1){ cover.add(new Point(pol1[i].x,pol1[i].y)); } } } } for(int i=0;i< pol1.length;i++){//遍历得到交点 for(int j=0;j<pol2.length;j++){ if(line.loc(pol2[j].x,pol2[j].y,pol2[(j+1)% pol2.length].x,pol2[(j+1)% pol2.length].y,pol1[i].x,pol1[i].y)==0){ if(line.isOnLine(pol2[j].x,pol2[j].y,pol2[(j+1)% pol2.length].x,pol2[(j+1)% pol2.length].y,pol1[i].x,pol1[i].y)) { cover.add(new Point(pol1[i].x, pol1[i].y)); } } } } for(int i=0;i< pol2.length;i++){ for(int j=0;j<pol1.length;j++){ if(line.loc(pol1[j].x,pol1[j].y,pol1[(j+1)% pol1.length].x,pol1[(j+1)% pol1.length].y,pol2[i].x,pol2[i].y)==0){ if(line.isOnLine(pol1[j].x,pol1[j].y,pol1[(j+1)% pol1.length].x,pol1[(j+1)% pol1.length].y,pol2[i].x,pol2[i].y)) { cover.add(new Point(pol2[i].x, pol2[i].y)); } } } } Point[] coverPol = new Point[cover.size()]; kk=0; for(Point t:cover){ coverPol[kk++] = t; } double[] theta = new double[coverPol.length]; double[] theTa = new double[coverPol.length]; double[] X = new double[coverPol.length]; double[] Y = new double[coverPol.length]; double x=coverPol[0].x; double y=coverPol[0].y; coverPol[0].x=0; coverPol[0].y=0; for(int i=1;i<coverPol.length;i++){ coverPol[i].x -= x; coverPol[i].y -= y; X[i] = coverPol[i].x; Y[i] = coverPol[i].y; theta[i] = Math.atan2(coverPol[i].y,coverPol[i].x); theTa[i] = Math.atan2(coverPol[i].y,coverPol[i].x); } Arrays.sort(theta); boolean[] used = new boolean[coverPol.length]; int[] loc = new int[coverPol.length]; int[] pre = new int[coverPol.length]; for(int i=0;i<coverPol.length;i++){ for(int j=0;j<coverPol.length;j++){ if(theTa[i] == theta[j] && !used[j]){ used[j] = true; loc[i] = j; pre[j] = i; break; } } } double[] xx = new double[coverPol.length-1]; double[] yy = new double[coverPol.length-1]; int k = 0; for(int i=0;i<coverPol.length;i++){ if(!line.pointCoincide(X[pre[i]],Y[pre[i]],0.0,0.0)){ xx[k] = X[pre[i]]; yy[k] = Y[pre[i]]; k++; } } double S=0; for(int i=0;i<coverPol.length-2;i++){//求面积 S += triangle.qinjiushao(0, 0, xx[i], yy[i], xx[(i+1)%(coverPol.length-1)], yy[(i+1)%(coverPol.length-1)]); } BigDecimal Ss = new BigDecimal(S); S = Ss.setScale(3,BigDecimal.ROUND_HALF_UP).doubleValue(); System.out.println(S); break; case '6': if(ss.length!=6) { if (cnt != ss.length) System.out.println("Wrong Format"); else System.out.println("wrong number of points"); return; } str=ss[0].split(",");x6=Double.parseDouble(str[0]);y6=Double.parseDouble(str[1]); str=ss[1].split(",");x1=Double.parseDouble(str[0]);y1=Double.parseDouble(str[1]); str=ss[2].split(",");x2=Double.parseDouble(str[0]);y2=Double.parseDouble(str[1]); str=ss[3].split(",");x3=Double.parseDouble(str[0]);y3=Double.parseDouble(str[1]); str=ss[4].split(",");x4=Double.parseDouble(str[0]);y4=Double.parseDouble(str[1]); str=ss[5].split(",");x5=Double.parseDouble(str[0]);y5=Double.parseDouble(str[1]); LinkedHashSet<Point>set6 = new LinkedHashSet<>(); set6.add(new Point(x1,y1)); set6.add(new Point(x2,y2)); set6.add(new Point(x3,y3)); set6.add(new Point(x4,y4)); set6.add(new Point(x5,y5)); if(set6.size()==3){ Point[] case6 = new Point[3]; int q=0; for(Point r:set6){ case6[q++]=r; } x1=case6[0].x;y1=case6[0].y; x2=case6[1].x;y2=case6[1].y; x3=case6[2].x;y3=case6[2].y; triangle.Case6(x1,y1,x2,y2,x3,y3,x6,y6); } else if(set6.size()==4){ Point[] case6 = new Point[4]; int q=0; for(Point r:set6){ case6[q++]=r; } x1=case6[0].x;y1=case6[0].y; x2=case6[1].x;y2=case6[1].y; x3=case6[2].x;y3=case6[2].y; x4=case6[3].x;y4=case6[3].y; if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ triangle.Case6(x1,y1,x3,y3,x4,y4,x6,y6); } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ triangle.Case6(x1,y1,x2,y2,x4,y4,x6,y6); } else if(line.isParad(x3,y3,x4,y4,x4,y4,x1,y1)){ triangle.Case6(x1,y1,x2,y2,x3,y3,x6,y6); } else if(line.isParad(x4,y4,x1,y1,x1,y1,x2,y2)){ triangle.Case6(x2,y2,x3,y3,x4,y4,x6,y6); } else{ quadrilateral.Case6(x1,y1,x2,y2,x3,y3,x4,y4,x6,y6); } } else{ if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x1,y1,x5,y5,x5,y5,x4,y4)){ triangle.Case6(x1,y1,x3,y3,x4,y4,x6,y6); } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ triangle.Case6(x1,y1,x3,y3,x5,y5,x6,y6); } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)){ triangle.Case6(x1,y1,x2,y2,x4,y4,x6,y6); } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ triangle.Case6(x1,y1,x4,y4,x5,y5,x6,y6); } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ triangle.Case6(x1,y1,x2,y2,x5,y5,x6,y6); } else if(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)){ triangle.Case6(x1,y1,x3,y3,x4,y4,x6,y6); } else if(line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)&&line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ triangle.Case6(x2,y2,x3,y3,x4,y4,x6,y6); } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ quadrilateral.Case6(x1,y1,x3,y3,x4,y4,x5,y5,x6,y6); } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ quadrilateral.Case6(x1,y1,x2,y2,x4,y4,x5,y5,x6,y6); } else if(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ quadrilateral.Case6(x1,y1,x2,y2,x3,y3,x5,y5,x6,y6); } else if(line.isParad(x1,y1,x5,y5,x5,y5,x4,y4)){ quadrilateral.Case6(x1,y1,x2,y2,x3,y3,x4,y4,x6,y6); } else{ pentagon.Case6(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6); } } } } static Point[] getPoint(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//得到去重、去平行后的点集 Line line = new Line(); Triangle triangle = new Triangle(); Quadrilateral quadrilateral = new Quadrilateral(); Pentagon pentagon = new Pentagon(); LinkedHashSet<Point>set = new LinkedHashSet<>(); set.add(new Point(x1,y1)); set.add(new Point(x2,y2)); set.add(new Point(x3,y3)); set.add(new Point(x4,y4)); set.add(new Point(x5,y5)); if(set.size()==3){ Point[] res = new Point[3]; int k=0; for(Point r:set){ res[k++]=r; } return res; } else if(set.size()==4){ Point[] res = new Point[4]; int k=0; for(Point r:set){ res[k++]=r; } return res; } else{ Point[] res = new Point[5]; int k=0; for(Point r:set){ res[k++]=r; } return res; } } static Point[] xingzhuang(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//得到有效点集 Line line = new Line(); Triangle triangle = new Triangle(); Quadrilateral quadrilateral = new Quadrilateral(); Pentagon pentagon = new Pentagon(); Point[] res = new Point[5]; res = getPoint(x1, y1, x2, y2, x3, y3, x4, y4, x5, y5); if(res.length==3){ return res; } else if(res.length==4){ x1=res[0].x;y1=res[0].y; x2=res[1].x;y2=res[1].y; x3=res[2].x;y3=res[2].y; x4=res[3].x;y4=res[3].y; if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x3,y3); res3[2]=new Point(x4,y4); return res3; } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x2,y2); res3[2]=new Point(x4,y4); return res3; } else if(line.isParad(x3,y3,x4,y4,x4,y4,x1,y1)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x2,y2); res3[2]=new Point(x3,y3); return res3; } else if(line.isParad(x4,y4,x1,y1,x1,y1,x2,y2)){ Point[] res3 = new Point[3]; res3[0]=new Point(x2,y2); res3[1]=new Point(x3,y3); res3[4]=new Point(x4,y4); return res3; } else{ Point[] res4 = new Point[4]; res4[0]=new Point(x1,y1); res4[1]=new Point(x2,y2); res4[2]=new Point(x3,y3); res4[3]=new Point(x4,y4); return res4; } } else{ if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x1,y1,x5,y5,x5,y5,x4,y4)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x3,y3); res3[2]=new Point(x4,y4); return res3; } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x3,y3); res3[2]=new Point(x5,y5); return res3; } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x2,y2); res3[2]=new Point(x4,y4); return res3; } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)&&line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x4,y4); res3[2]=new Point(x5,y5); return res3; } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)&&line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x2,y2); res3[2]=new Point(x5,y5); return res3; } else if(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)&&line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)){ Point[] res3 = new Point[3]; res3[0]=new Point(x1,y1); res3[1]=new Point(x2,y2); res3[2]=new Point(x3,y3); return res3; } else if(line.isParad(x4,y4,x5,y5,x5,y5,x1,y1)&&line.isParad(x5,y5,x1,y1,x1,y1,x2,y2)){ Point[] res3 = new Point[3]; res3[0]=new Point(x2,y2); res3[1]=new Point(x3,y3); res3[2]=new Point(x4,y4); return res3; } else if(line.isParad(x1,y1,x2,y2,x2,y2,x3,y3)){ Point[] res4 = new Point[4]; res4[0]=new Point(x1,y1); res4[1]=new Point(x3,y3); res4[2]=new Point(x4,y4); res4[3]=new Point(x5,y5); return res4; } else if(line.isParad(x2,y2,x3,y3,x3,y3,x4,y4)){ Point[] res4 = new Point[4]; res4[0]=new Point(x1,y1); res4[1]=new Point(x2,y2); res4[2]=new Point(x4,y4); res4[3]=new Point(x5,y5); return res4; } else if(line.isParad(x3,y3,x4,y4,x4,y4,x5,y5)){ Point[] res4 = new Point[4]; res4[0]=new Point(x1,y1); res4[1]=new Point(x2,y2); res4[2]=new Point(x3,y3); res4[3]=new Point(x5,y5); return res4; } else if(line.isParad(x1,y1,x5,y5,x5,y5,x4,y4)){ Point[] res4 = new Point[4]; res4[0]=new Point(x1,y1); res4[1]=new Point(x2,y2); res4[2]=new Point(x3,y3); res4[3]=new Point(x4,y4); return res4; } else{ Point[] res5 = new Point[5]; res5[0]=new Point(x1,y1); res5[1]=new Point(x2,y2); res5[2]=new Point(x3,y3); res5[3]=new Point(x4,y4); res5[4]=new Point(x5,y5); return res5; } } } } class Point{//点类 double x,y; public Point(double x,double y){ this.x=x; this.y=y; } @Override public boolean equals(Object t){ if(this == t){ return true; } if(t == null || getClass() != t.getClass()){ return false; } Point point = (Point) t; return x == point.x && y == point.y &&Objects.equals(x,point.x) && Objects.equals(y,point.y); } @Override public int hashCode(){ return Objects.hash(x,y); } } class Line{//线类 boolean cross(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//判断线段是否相交 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A34=y3-y4; double B34=x4-x3; double C34=x3*y4-x4*y3; double D=A12*B34-A34*B12; if(Math.abs(D)>=0.0000001){ double x=(B12*C34-B34*C12)/D; double y=(A34*C12-A12*C34)/D; if(((x<=Math.max(x1,x2)&&x>=Math.min(x1,x2)&&y<Math.max(y1,y2)&&y>Math.min(y1,y2))||(x<Math.max(x1,x2)&&x>Math.min(x1,x2)&&y<=Math.max(y1,y2)&&y>=Math.min(y1,y2)))&&((x<=Math.max(x3,x4)&&x>=Math.min(x3,x4)&&y<Math.max(y3,y4)&&y>Math.min(y3,y4))||(x<Math.max(x3,x4)&&x>Math.min(x3,x4)&&y<=Math.max(y3,y4)&&y>=Math.min(y3,y4)))){ return true; } } return false; } boolean cross1(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){ double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A34=y3-y4; double B34=x4-x3; double C34=x3*y4-x4*y3; double D=A12*B34-A34*B12; if(Math.abs(D)>=0.0000001){ double x=(B12*C34-B34*C12)/D; double y=(A34*C12-A12*C34)/D; if((x<=Math.max(x1,x2)&&x>=Math.min(x1,x2)&&y<Math.max(y1,y2)&&y>Math.min(y1,y2))||(x<Math.max(x1,x2)&&x>Math.min(x1,x2)&&y<=Math.max(y1,y2)&&y>=Math.min(y1,y2))){ return true; } } return false; } boolean isParad(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//是否平行 if((y2-y1)*(x4-x3)==(y4-y3)*(x2-x1)){ return true; } return false; } boolean pointCoincide(double x1,double y1,double x2,double y2){//点重 if(x1-x2==0&&y1-y2==0){ return true; } return false; } int loc(double x1,double y1,double x2,double y2,double x3,double y3){//位置关系 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; if(Math.abs(A12*x3+B12*y3+C12)<0.0000001){ return 0; } else if(A12*x3+B12*y3+C12<0){ return -1; } else{ return 1; } } boolean isOnLine(double x1,double y1,double x2,double y2,double x3,double y3){//是否在线段上 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; if(Math.abs(A12*x3+B12*y3+C12)<0.0000001){ if(x3>=Math.min(x1,x2)&&x3<=Math.max(x1,x2)&&y3>=Math.min(y1,y2)&&y3<=Math.max(y1,y2)){ return true; } } return false; } boolean lineCoincide(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//线重合 if(isParad(x1, y1, x2, y2, x3, y3, x4, y4)){ if(loc(x1, y1, x2, y2, x3, y3)==0&&loc(x1, y1, x2, y2, x4, y4)==0&&!pointCoincide(x3,y3,x4,y4)&&!pointCoincide(x1,y1,x2,y2)){ return true; } } return false; } Point tlpoint(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//得到交点 double A12=y1-y2; double B12=x2-x1; double C12=x1*y2-x2*y1; double A34=y3-y4; double B34=x4-x3; double C34=x3*y4-x4*y3; double D=A12*B34-A34*B12; double x=(B12*C34-B34*C12)/D; double y=(A34*C12-A12*C34)/D; return new Point(x,y); } } class Triangle{//三角形类 double qinjiushao(double x1,double y1,double x2,double y2,double x3,double y3){//求三角形面积 double a=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); double b=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); double c=Math.sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3)); double p=(a+b+c)/2; double s=Math.sqrt(p*(p-a)*(p-b)*(p-c)); return s; } int inTriangle(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//是否在三角形内 double s1=qinjiushao(x1,y1,x2,y2,x4,y4); double s2=qinjiushao(x1,y1,x3,y3,x4,y4); double s3=qinjiushao(x2,y2,x3,y3,x4,y4); double s=qinjiushao(x1,y1,x2,y2,x3,y3); if(Math.abs(s1+s2+s3-s)<0.0001){ if(Math.abs(s1)<0.0001||Math.abs(s2)<0.0001||Math.abs(s3)<0.0001){ return 0; } else{ return 1; } } else{ return -1; } } void Case6(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//是否在三角形内(case6) if(inTriangle(x1,y1,x2,y2,x3,y3,x4,y4)==1){ System.out.println("in the triangle"); } else if(inTriangle(x1, y1, x2, y2, x3, y3, x4, y4)==0){ System.out.println("on the triangle"); } else{ System.out.println("outof the triangle"); } } } class Quadrilateral{//四边形类 int inQuarilateral(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//是否在四边形内 Triangle triangle = new Triangle(); double s1=triangle.qinjiushao(x1,y1,x2,y2,x5,y5); double s2=triangle.qinjiushao(x2,y2,x3,y3,x5,y5); double s3=triangle.qinjiushao(x3,y3,x4,y4,x5,y5); double s4=triangle.qinjiushao(x1,y1,x4,y4,x5,y5); double s=triangle.qinjiushao(x1,y1,x2,y2,x3,y3)+ triangle.qinjiushao(x1,y1,x3,y3,x4,y4); if(Math.abs(s1+s2+s3+s4-s)<0.0001){ if(Math.abs(s1)<0.0001||Math.abs(s2)<0.0001||Math.abs(s3)<0.0001||Math.abs(s4)<0.0001){ return 0; } return 1; } else{ return -1; } } void Case6(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5){//是否在四边形内/边上/外(case6) if(inQuarilateral(x1, y1, x2, y2, x3, y3, x4, y4, x5, y5)==1){ System.out.println("in the quadrilateral"); } else if(inQuarilateral(x1, y1, x2, y2, x3, y3, x4, y4, x5, y5)==0){ System.out.println("on the quadrilateral"); } else{ System.out.println("outof the quadrilateral"); } } } class Pentagon {//五边形类 int inPentagon(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5,double x6,double y6){ Triangle triangle = new Triangle(); double s1=triangle.qinjiushao(x1,y1,x2,y2,x6,y6); double s2=triangle.qinjiushao(x2,y2,x3,y3,x6,y6); double s3=triangle.qinjiushao(x3,y3,x4,y4,x6,y6); double s4=triangle.qinjiushao(x4,y4,x5,y5,x6,y6); double s5=triangle.qinjiushao(x1,y1,x5,y5,x6,y6); double s=triangle.qinjiushao(x1,y1,x2,y2,x3,y3)+ triangle.qinjiushao(x1,y1,x3,y3,x4,y4)+ triangle.qinjiushao(x1,y1,x4,y4,x5,y5); if(Math.abs(s1+s2+s3+s4+s5-s)<0.0000001){ if(Math.abs(s1)<0.0000001||Math.abs(s2)<0.0000001||Math.abs(s3)<0.0000001||Math.abs(s4)<0.0000001||Math.abs(s5)<0.0000001){ return 0; } return 1; } else{ return -1; } } void Case6(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5,double x6,double y6){ if(inPentagon(x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6)==1){ System.out.println("in the pentagon"); } else if(inPentagon(x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6)==0){ System.out.println("on the pentagon"); } else{ System.out.println("outof the pentagon"); } } }
上sourcemonitor分析!
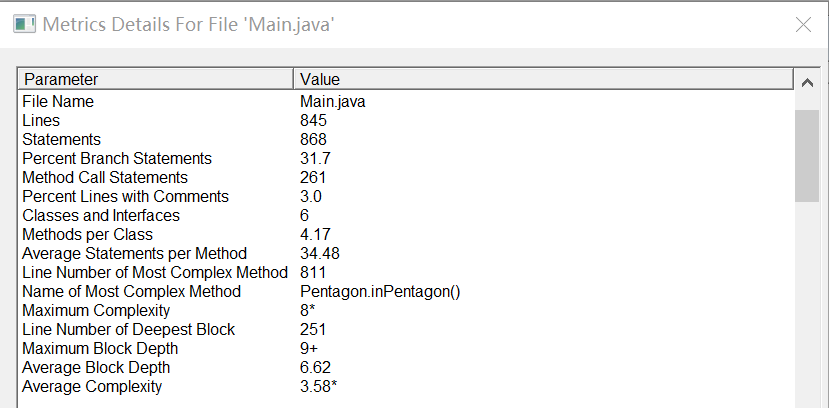

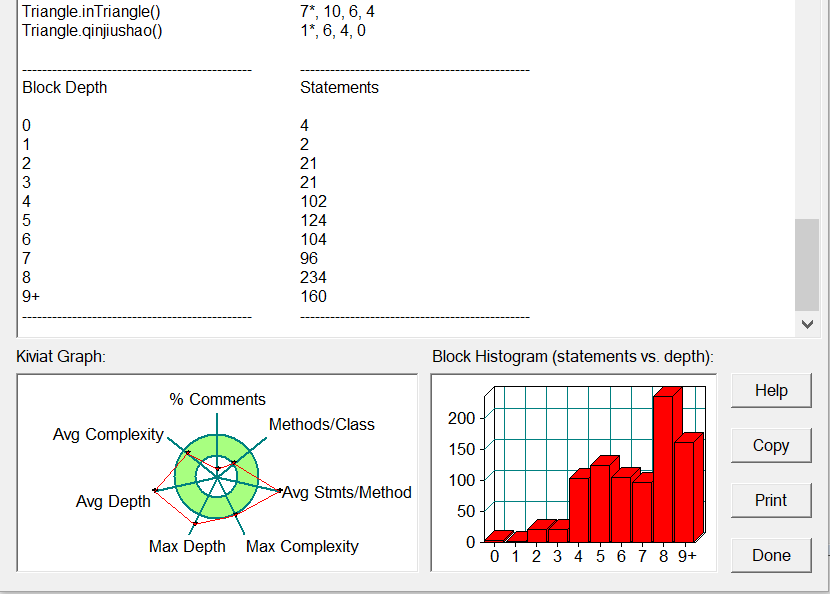
复杂度降了不少啊!庆祝一下行数也控制得不错。。
同时我们还能看到,该题代码对于类与方法的使用有所增加,深度有所增加。
总结:点线形系列最难的题,除了case4有点搞心态,其它都还好。当然case5的方法正确性有待商榷,因为存在重合部分多边形为凹多边形的情况,这里就不讨论了。
期中考试T1
题面:
-
设计一个类表示平面直角坐标系上的点Point,私有属性分别为横坐标x与纵坐标y,数据类型均为实型数,除构造方法以及属性的getter与setter方法外,定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息,格式如下:
(x,y),数值保留两位小数。为简化题目,其中,坐标点的取值范围设定为(0,200]。若输入有误,系统则直接输出Wrong Format -
设计一个类表示平面直角坐标系上的线Line,私有属性除了标识线段两端的点point1、point2外,还有一个字符串类型的color,用于表示该线段的颜色,同样,除构造方法以及属性的getter与setter方法外,定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息,输出格式如下:
``` The line's color is:颜色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:长度值 ```其中,所有数值均保留两位小数,建议可用
String.format("%.2f", data)方法。设计类图如下图所示。
** 题目要求:在主方法中定义一条线段对象,从键盘输入该线段的起点坐标与终点坐标以及颜色,然后调用该线段的display()方法进行输出。**
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red输出样例1:
在这里给出相应的输出。例如:
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96果不其然,期中考试仍然和点线形紧密联系。只用照着类图写就行了。
我滴代码
import java.util.*; import java.lang.*; public class Main { public static void main(String[] args){ Scanner bjsn = new Scanner(System.in); double x1,y1,x2,y2; String s; x1 = bjsn.nextDouble(); y1 = bjsn.nextDouble(); x2 = bjsn.nextDouble(); y2 = bjsn.nextDouble(); s = bjsn.next(); if(x1 <= 0 || x1 > 200 || x2 <= 0 || x2 > 200 || y1 <= 0 || y1 > 200 || y2 <= 0 || y2 > 200 ){ System.out.println("Wrong Format"); return; } Point p1 = new Point(x1,y1); Point p2 = new Point(x2,y2); Line line = new Line(p1,p2,s); line.setColor(s); line.display(); } } class Point{ double x; double y; public Point(double x,double y){ this.x = x; this.y = y; } public double getX(){ return this.x; } public double getY(){ return this.y; } public void setX(double x){ this.x = x; } public void setY(double y){ this.y = y; } public void display(){ System.out.println("("+String.format("%.2f",this.x)+","+String.format("%.2f",this.y)+")"); } } class Line{ Point p1,p2; String color; public Line(Point p1,Point p2,String color){ this.p1 = p1; this.p2 = p2; this.color = color; } public Point getPoint1(){ return this.p1; } public Point getPoint2(){ return this.p2; } public void setPoint1(Point p){ this.p1 = p; } public void setPoint2(Point p){ this.p2 = p; } public void setColor(String color){ this.color = color; } public String getColor(){ return this.color; } public double getDistance(Point p1,Point p2){ return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); } public void display(){ System.out.println("The line's color is:"+color); System.out.println("The line's begin point's Coordinate is:"); p1.display(); System.out.println("The line's end point's Coordinate is:"); p2.display(); System.out.println("The line's length is:"+String.format("%.2f",getDistance(p1,p2))); } }
一道非常直球的题,直接上sourcemonitor分析:
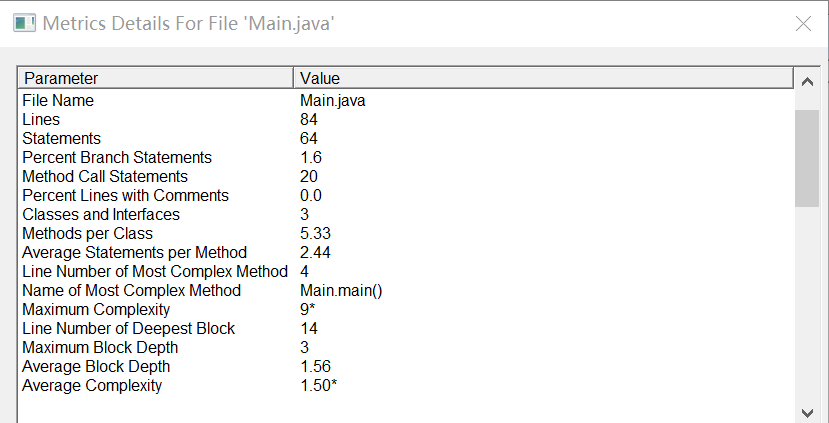

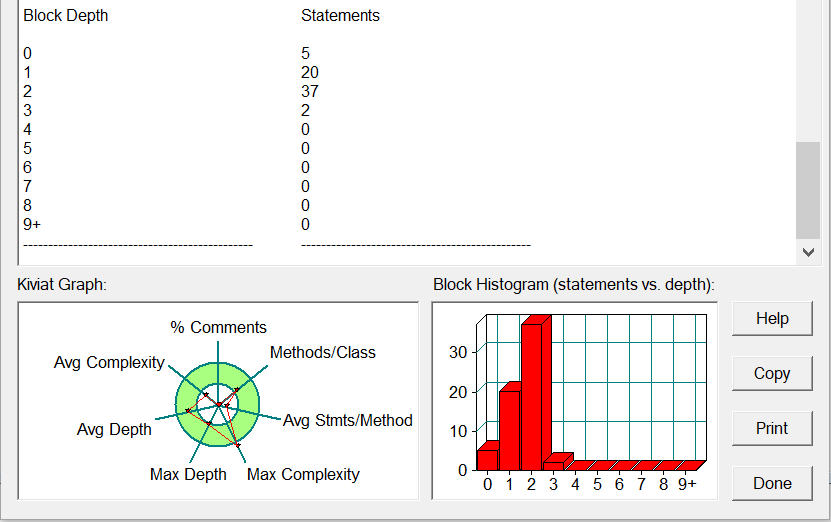
照类图写代码质量低不了
期中考试T2
题面:
在“点与线(类设计)”题目基础上,对题目的类设计进行重构,以实现继承与多态的技术性需求。
- 对题目中的点Point类和线Line类进行进一步抽象,定义一个两个类的共同父类Element(抽象类),将display()方法在该方法中进行声明(抽象方法),将Point类和Line类作为该类的子类。
- 再定义一个Element类的子类面Plane,该类只有一个私有属性颜色color,除了构造方法和属性的getter、setter方法外,display()方法用于输出面的颜色,输出格式如下:
The Plane's color is:颜色 - 在主方法内,定义两个Point(线段的起点和终点)对象、一个Line对象和一个Plane对象,依次从键盘输入两个Point对象的起点、终点坐标和颜色值(Line对象和Plane对象颜色相同),然后定义一个Element类的引用,分别使用该引用调用以上四个对象的display()方法,从而实现多态特性。示例代码如下:
element = p1;//起点Point element.display(); element = p2;//终点Point element.display(); element = line;//线段 element.display(); element = plane;//面 element.display();类结构如下图所示。
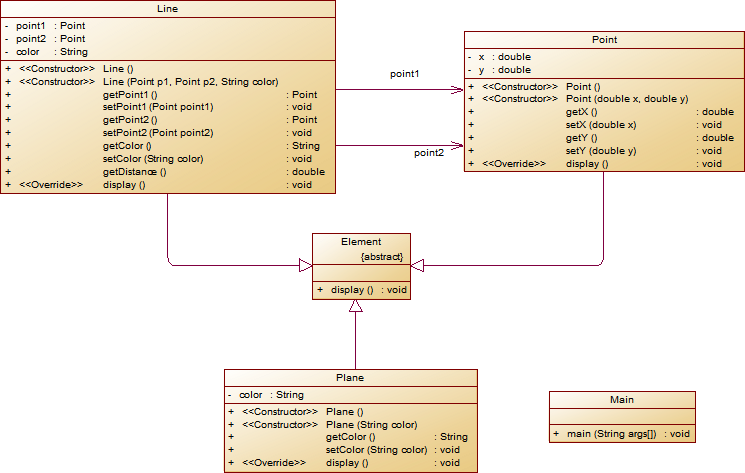
其中,所有数值均保留两位小数,建议可用String.format("%.2f", data)方法。
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值
输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red
输出样例1:
在这里给出相应的输出。例如:
(5.00,9.40)
(12.30,84.00)
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
The Plane's color is:Red我滴代码
import java.util.*; import java.lang.*; public class Main { public static void main(String[] args){ Scanner bjsn = new Scanner(System.in); double x1,y1,x2,y2; String s; x1 = bjsn.nextDouble(); y1 = bjsn.nextDouble(); x2 = bjsn.nextDouble(); y2 = bjsn.nextDouble(); s = bjsn.next(); if(x1 <= 0 || x1 > 200 || x2 <= 0 || x2 > 200 || y1 <= 0 || y1 > 200 || y2 <= 0 || y2 > 200 ){ System.out.println("Wrong Format"); return; } Point p1 = new Point(x1,y1); Point p2 = new Point(x2,y2); Line line = new Line(p1,p2,s); Plane plane = new Plane(s); p1.display(); p2.display(); line.display(); plane.display(); } } abstract class Element{ public abstract void display(); } class Point extends Element{ double x; double y; public Point(double x,double y){ this.x = x; this.y = y; } public double getX(){ return this.x; } public double getY(){ return this.y; } public void setX(double x){ this.x = x; } public void setY(double y){ this.y = y; } @Override public void display(){ System.out.println("("+String.format("%.2f",this.x)+","+String.format("%.2f",this.y)+")"); } } class Line extends Element{ Point p1,p2; String color; public Line(Point p1,Point p2,String color){ this.p1 = p1; this.p2 = p2; this.color = color; } public Point getPoint1(){ return this.p1; } public Point getPoint2(){ return this.p2; } public void setPoint1(Point p){ this.p1 = p; } public void setPoint2(Point p){ this.p2 = p; } public void setColor(String color){ this.color = color; } public String getColor(){ return this.color; } public double getDistance(Point p1,Point p2){ return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); } @Override public void display(){ System.out.println("The line's color is:"+color); System.out.println("The line's begin point's Coordinate is:"); p1.display(); System.out.println("The line's end point's Coordinate is:"); p2.display(); System.out.println("The line's length is:"+String.format("%.2f",getDistance(p1,p2))); } } class Plane extends Element{ String color; public Plane(String color){ this.color = color; } public String getColor(){ return this.color; } public void setColor(String s){ this.color = s; } @Override public void display(){ System.out.println("The Plane's color is:"+color); } }
同样直球的一道题,sourcemonitor分析:
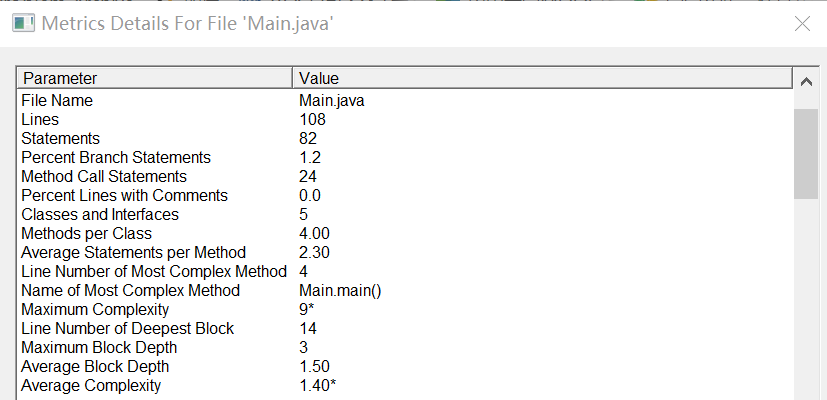

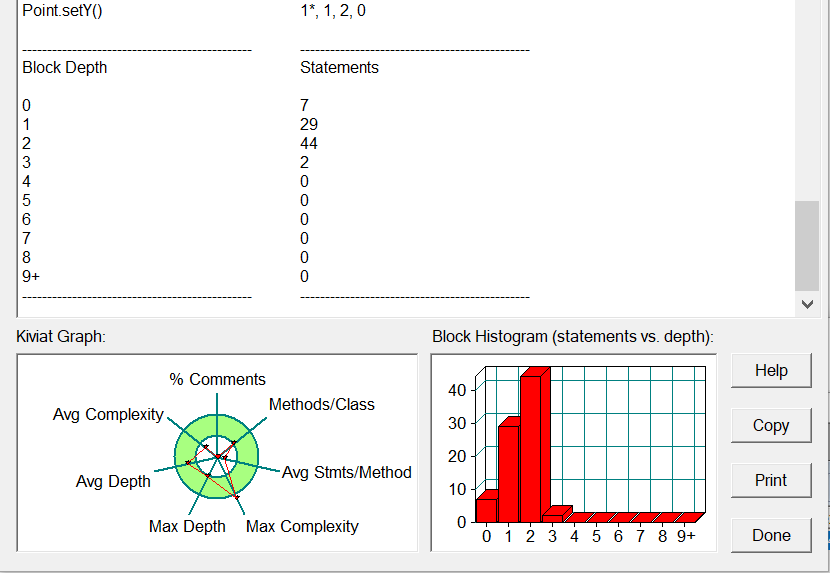
期中考试T3
题面:
在“点与线(继承与多态)”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
- 在原有类设计的基础上,增加一个GeometryObject容器类,其属性为
ArrayList<Element>类型的对象(若不了解泛型,可以不使用<Element>) - 增加该类的
add()方法及remove(int index)方法,其功能分别为向容器中增加对象及删除第index - 1(ArrayList中index>=0)个对象 - 在主方法中,用户循环输入要进行的操作(choice∈[0,4]),其含义如下:
- 1:向容器中增加Point对象
- 2:向容器中增加Line对象
- 3:向容器中增加Plane对象
- 4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
- 0:输入结束
choice = input.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list ... break; case 2://insert Line object into list ... break; case 3://insert Plane object into list ... break; case 4://delete index - 1 object from list int index = input.nextInt(); ... } choice = input.nextInt(); }输入结束后,按容器中的对象顺序分别调用每个对象的display()方法进行输出。
类图如下所示:
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
switch(choice) {
case 1://insert Point object into list
输入“点”对象的x,y值
break;
case 2://insert Line object into list
输入“线”对象两个端点的x,y值
break;
case 3://insert Plane object into list
输入“面”对象的颜色值
break;
case 4://delete index - 1 object from list
输入要删除的对象位置(从1开始)
...
}
输出格式:
- Point、Line、Plane的输出参考题目2
- 删除对象时,若输入的index超出合法范围,程序自动忽略该操作
输入样例:
在这里给出一组输入。例如:
1
3.4
5.6
2
4.4
8.0
0.98
23.888
Red
3
Black
1
9.8
7.5
3
Green
4
3
0输出样例:
在这里给出相应的输出。例如:
(3.40,5.60)
The line's color is:Red
The line's begin point's Coordinate is:
(4.40,8.00)
The line's end point's Coordinate is:
(0.98,23.89)
The line's length is:16.25
(9.80,7.50)
The Plane's color is:Green我滴代码:
import java.util.*; import java.lang.*; public class Main { public static void main(String[] args){ Scanner bjsn = new Scanner(System.in); double x1,y1,x2,y2; String s; GeometryObject geometryObject = new GeometryObject(); while(true) { int op = bjsn.nextInt(); if(op == 0){ break; } switch (op) { case 1: x1 = bjsn.nextDouble(); y1 = bjsn.nextDouble(); if (x1 <= 0 || x1 > 200 || y1 <= 0 || y1 > 200) { System.out.println("Wrong Format"); return; } Point p1 = new Point(x1, y1); geometryObject.add(p1); break; case 2: x1 = bjsn.nextDouble(); y1 = bjsn.nextDouble(); x2 = bjsn.nextDouble(); y2 = bjsn.nextDouble(); String t = bjsn.next(); if (x1 <= 0 || x1 > 200 || x2 <= 0 || x2 > 200 || y1 <= 0 || y1 > 200 || y2 <= 0 || y2 > 200) { System.out.println("Wrong Format"); return; } Line line = new Line(new Point(x1,y1),new Point(x2,y2),t); geometryObject.add(line); break; case 3: String tt = bjsn.next(); geometryObject.add(new Plane(tt)); break; case 4: int index = bjsn.nextInt(); if(index >= geometryObject.getList().size() || index < 1){ break; } geometryObject.remove(index - 1); break; } } ArrayList<Element>arr = geometryObject.getList(); for(int i = 0; i < arr.size() ;i++){ arr.get(i).display(); } } } abstract class Element{ public abstract void display(); } class Point extends Element{ double x; double y; public Point(double x,double y){ this.x = x; this.y = y; } public double getX(){ return this.x; } public double getY(){ return this.y; } public void setX(double x){ this.x = x; } public void setY(double y){ this.y = y; } @Override public void display(){ System.out.println("("+String.format("%.2f",this.x)+","+String.format("%.2f",this.y)+")"); } } class Line extends Element{ Point p1,p2; String color; public Line(Point p1,Point p2,String color){ this.p1 = p1; this.p2 = p2; this.color = color; } public Point getPoint1(){ return this.p1; } public Point getPoint2(){ return this.p2; } public void setPoint1(Point p){ this.p1 = p; } public void setPoint2(Point p){ this.p2 = p; } public void setColor(String color){ this.color = color; } public String getColor(){ return this.color; } public double getDistance(Point p1,Point p2){ return Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); } @Override public void display(){ System.out.println("The line's color is:"+color); System.out.println("The line's begin point's Coordinate is:"); p1.display(); System.out.println("The line's end point's Coordinate is:"); p2.display(); System.out.println("The line's length is:"+String.format("%.2f",getDistance(p1,p2))); } } class Plane extends Element{ String color; public Plane(String color){ this.color = color; } public String getColor(){ return this.color; } public void setColor(String s){ this.color = s; } @Override public void display(){ System.out.println("The Plane's color is:"+color); } } class GeometryObject{ ArrayList<Element>arr = new ArrayList<>(); public void add(Element element){ arr.add(element); } public void remove(int index){ arr.remove(index); } public ArrayList<Element>getList(){ return arr; } }
话不多说,上sourcemonitor分析:

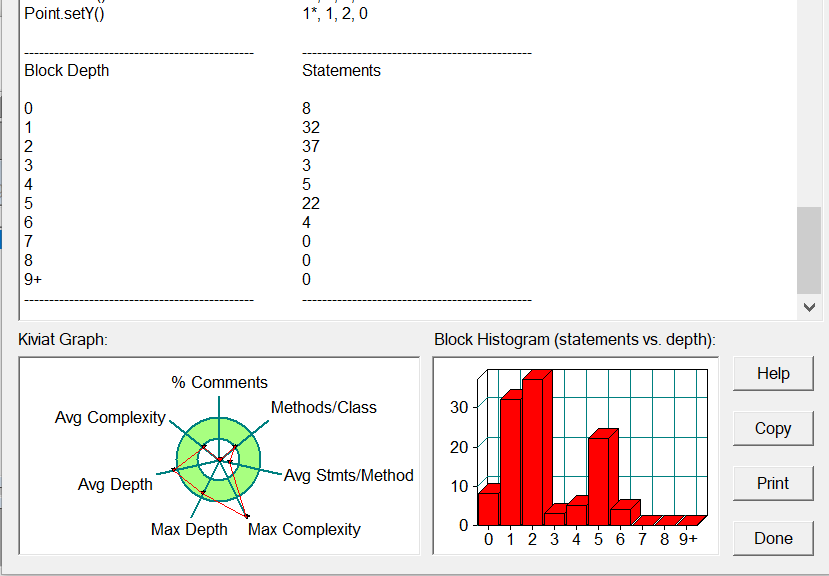
三、踩坑心得
纵观本博客所分析的两次作业和一次考试,踩过的坑数不胜数。下面来罗列一遍吧——
(1)第四次大作业T2
1.计算四边形分割面积时,按顺序传入四个点,忘记存在分割线与四边形某条边平行的情况,导致一直过不了题给样例
2.case41,43什么都考虑到了,除了本应相邻线段相交,本应相邻两点构成直线与x/y轴平行这一情况,导致大WA特WA,为此代码重构了十次甚至九次吧。。
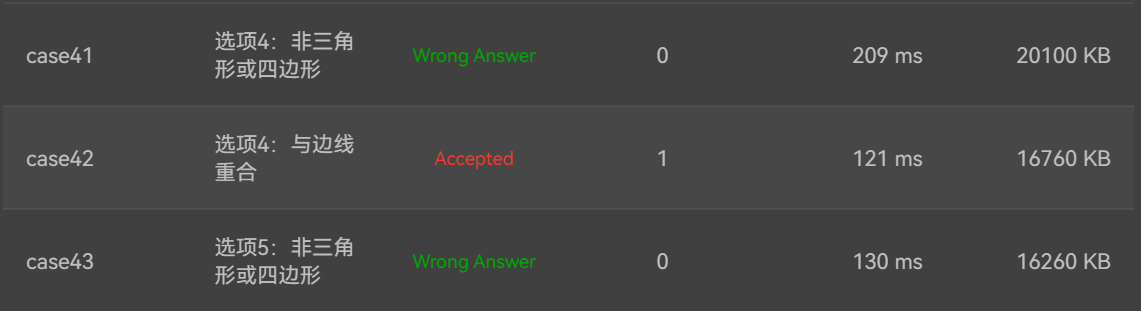
case41、43:
即本应相邻线段相交,本应相邻两点构成直线与x/y轴平行。
WA了好多发才发现。。
![]()
![]()
第二张图截不下了,就放这么多吧。。具体看代码
(2)第五次大作业T1
1.因为没有判重函数/容器,(自己瞎判断的)导致一直WA。由于分类讨论的情况非常多,自己在写各种判重、数点时写了很多冗余代码,同时也让自己云里雾里。多学点容器和其它的java库的功能吧,再怎样也比自己写的可靠。
(3)第五次大作业T2
1.上来就写的case6,结果开头几发就出师不利啊,各种漏情况。。。
2.case5遗漏一个多边形顶点在另一个的边上这种情况。
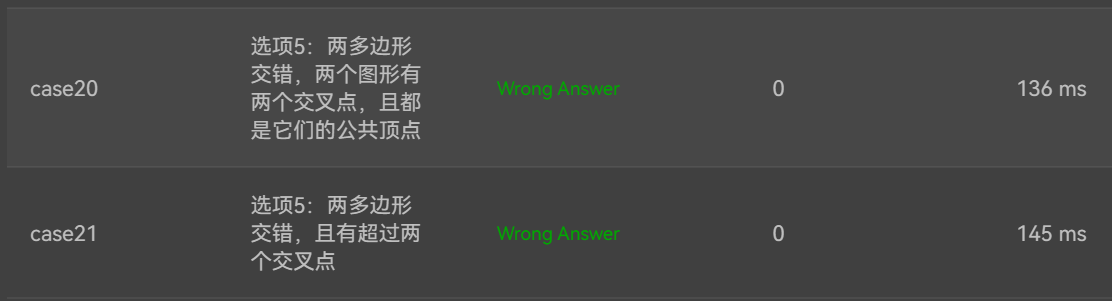
(4)期中考试
读取字符串(排除空格)一定要用next()!!!考试时没意识到这点,用的nextLine(),导致表示颜色的字符串一直无法读入,The color of ... is:后一直没有输出。最后只好写了一个排除空格的输入处理模块,但还是WA了。。。还耽误了大量时间。
![]()
![]()
四、改进建议
从代码的可读性、sourcemonitor分析结果来看,作业代码仍存在复杂度较高的情况,可读性不强,可从如下方面改进:
1.写代码前画好类图。画出类图能给你一个清晰的编程思路,知道哪些地方改写哪些东西。
2.善于使用继承和抽象。对于多个具有相似属性的类,类似功能可以添加到抽象类里,既可缩短代码方便代码阅读,又可简化编程。
五、总结
这两次大作业,以及随后的期中考试,让我深深地体会到了类、继承、抽象等面向对象程序设计方法的好处。山重水复疑无路,柳暗花明又一村,调试代码的过程无疑是漫长而痛苦的,但在AC瞬间的喜悦感是无法形容的。同时,这几次作业还让我意识到,想要学好java(其它专业课也一样),必须系统、广泛地学习,接受新的思维和方法,不能揪着一个不符合时宜的习惯(如用面向过程的方法写java程序)不放;同时还要多思考,多上手操作。学而不思则罔,思而不学则殆。最后在此感谢老师同学对我java学习所提供的帮助!



