nchu-software-oop-2022前三次大作业总结
一、前言
目前已完成的3次java大作业均以基本java语法的考查为主。第一次大作业由9道入门语法题组成,题量虽大但题目非常简单,只需if、else或其它一些操作即可实现,很快就能写完。唯一要注意的便是double类型的数输出时要转化为float类型,可能是精度问题吧。。第二次作业以字符串处理为主,难度偏易,只需按照题意模拟即可。从第三次作业开始,题目难度陡然提升。首先是正则输入法判断输入是否符合格式(光这一点我就被卡了很久hh),多敲了很多冤枉代码。第三次大作业思维难度不高,主要难点在于实现。那些纷繁复杂的样例测试点,更像是在考查我们思路的严谨性,以及我们的耐心。(写多了C/C++,代码主要还是面向过程方法,下次一定用类写)
本篇博客将对三次作业中最具代表性的四道题(第二次作业T2,第三次作业的全部题目)进行分析与总结。
二、设计分析
第二次大作业T2
题面
RS232是串口常用的通信协议,在异步通信模式下,串口可以一次发送5~8位数据,收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位),发送方有数据发送时,会在有效数据(5~8位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序,模拟串口接收处理程序,注:假定有效数据是8位,奇偶校验位采用奇校验。
输入格式:
由0、1组成的二进制数据流。例如:11110111010111111001001101111111011111111101111
输出格式:
过滤掉空闲、起始、结束以及奇偶校验位之后的数据,数据之前加上序号和英文冒号。
如有多个数据,每个数据单独一行显示。
若数据不足11位或者输入数据全1没有起始位,则输出"null data",
若某个数据的结束符不为1,则输出“validate error”。
若某个数据奇偶校验错误,则输出“parity check error”。
若数据结束符和奇偶校验均不合格,输出“validate error”。
如:11011或11111111111111111。
例如:
1:11101011
2:01001101
3:validate error
输入样例:
在这里给出一组输入。例如:
1111011101011111111111
输出样例:
在这里给出相应的输出。例如:
1:11101011
输入样例1:
在这里给出一组输入。例如:
11110111010111111001001101111111011111111101111
输出样例1:
在这里给出相应的输出。例如:
1:11101011
2:01001101
3:validate error
代码
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner bjsn=new Scanner(System.in);
String s=bjsn.nextLine();
int len=s.length();
int pos=0,cnt=1,ans=0;
for(int i=0;i<len;i++){
if(s.charAt(i)=='0'){
ans++;
}
}
if(ans==0){//整个字串里没有出现数据
System.out.println("null data");
return;
}
if(len<11){//长度不够
System.out.println("null data");
return;
}
while(pos<len){//遍历字串
if(s.substring(pos,pos+1).equals("0")&&pos+10<len){
int res=0;
boolean flag=true;
for(int i=pos+1;i<=pos+9;i++){//截取8位字串进行分析
if(s.substring(i,i+1).equals("1")){
res++;
}
}
if(!s.substring(pos+10,pos+11).equals("1")){
flag=false;
}
if((res&1)==1&&flag){
System.out.println(cnt+":"+s.substring(pos+1,pos+9));
}
else{
if(flag){//奇偶校验未通过且校验位错误
System.out.println(cnt+":parity check error");
}
else{//奇偶校验未通过
System.out.println(cnt+":validate error");
}
}
pos+=11;
cnt++;
}
else{
pos++;
}
}
}
}
sourcemonitor分析
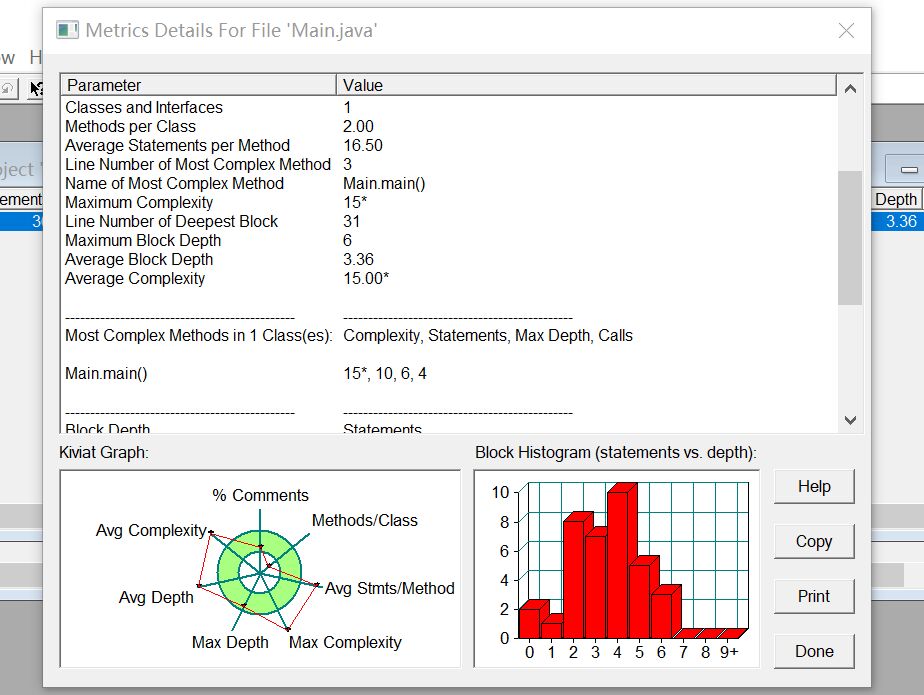
从sourcemonitor的源码分析来看,该代码类的使用极少,每一个函数包含的语句多,最大圈复杂度高,平均圈复杂度高,代码质量欠佳。代码实现过程中使用大量if-else,while等高复杂度语句。
总结:本题难度不大,细心分析即可。
第三次大作业T1
题面
输入连个点的坐标,计算两点之间的距离
输入格式:
4个double类型的实数,两个点的x,y坐标,依次是x1、y1、x2、y2,两个点的坐标之间以空格分隔,每个点的x,y坐标以英文“,”分隔。例如:0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法,输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个,输出“wrong number of points”。
输出格式:
计算所得的两点之间的距离。例如:1.4142135623730951
输入样例:
整数输入。例如:
0,0 1,1输出样例:
在这里给出相应的输出。例如:
1.4142135623730951输入样例1:
带符号double类型实数输入。例如:
+2,-2.3 0.9,-3.2输出样例1:
在这里给出相应的输出。例如:
1.42126704035519输入样例2:
格式非法。例如:
++2,-2.3 0.9,-3.2输出样例2:
在这里给出相应的输出。例如:
Wrong Format输入样例3:
点的数量超过两个。例如:
+2,-2.3 0.9,-3.2 +2,-2.3输出样例3:
在这里给出相应的输出。例如:
wrong number of points
代码
import java.util.*;
public class Main{
static Double P1=0.0,P2=0.0,Q1=0.0,Q2=0.0;
public static void main(String[] args){
Scanner bjsn=new Scanner(System.in);
String s=bjsn.nextLine();
int len=s.length();
int pos=0,t=0;
//输入格式判断
if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
String p1="",p2="",q1="",q2="";
String ss[]=s.split(" ");
String str[]=null;
for(String Str:ss){//提取逗号两端的字符串转为数字
str=Str.split(",");
for(String tt:str){
if(!tt.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){//正则表达式判断输入是否合法
System.out.println("Wrong Format");
return;
}
}
}
//本行起为不会正则表达式判断时写下的格式判断
if(s.charAt(pos)!='+'&&s.charAt(pos)!='-'&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'||(s.charAt(pos)>='0'&&s.charAt(pos)<='9')){
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'){
pos++;
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
p1+=s.charAt(pos);
pos++;
}
if(pos==len){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='.'){
p1+=".";
}
else if(s.charAt(pos)!=','){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)!=','){
pos++;
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
p1+=s.charAt(pos);
pos++;
}
if(pos==len){
System.out.println("Wrong Format");
return;
}
if(s.charAt(t)=='-'){
P1=-Double.parseDouble(p1);
}
else{
P1=Double.parseDouble(p1);
}
}
if(s.charAt(pos)!=','){
System.out.println("Wrong Format");
return;
}
pos++;
if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'||(s.charAt(pos)>='0'&&s.charAt(pos)<='9')){
t=pos;
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'){
pos++;
}
if(s.charAt(pos)<'0'||s.charAt(pos)>'9'){
System.out.println("Wrong Format");
return;
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
p2+=s.charAt(pos);
pos++;
}
if(pos==len){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='.'){
p2+=".";
}
else if(s.charAt(pos)!=' '){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='.'){
pos++;
if(s.charAt(pos)<'0'||s.charAt(pos)>'9'){
System.out.println("Wrong Format");
return;
}
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
p2+=s.charAt(pos);
pos++;
}
if(pos==len){
System.out.println("Wrong Format");
return;
}
if(s.charAt(t)=='-'){//提取数字
P2=-Double.parseDouble(p2);
}
else{
P2=Double.parseDouble(p2);
}
}
pos++;//后移
if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
t=pos;
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'||(s.charAt(pos)>='0'&&s.charAt(pos)<='9')){//判断是否数字
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'){
pos++;
}
if(s.charAt(pos)<'0'||s.charAt(pos)>'9'){
System.out.println("Wrong Format");
return;
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
q1+=s.charAt(pos);
pos++;
}
if(pos==len){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='.'){//判断小数
q1+=".";
}
else if(s.charAt(pos)!=','){
System.out.println("Wrong Format");//判断分隔符是否为逗号
return;
}
if(s.charAt(pos)=='.'){
pos++;
if(s.charAt(pos)<'0'||s.charAt(pos)>'9'){
System.out.println("Wrong Format");
return;
}
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
q1+=s.charAt(pos);
pos++;
}
if(pos==len){//超出长度且坐标信息尚未集齐
System.out.println("Wrong Format");
return;
}
if(s.charAt(t)=='-'){
Q1=-Double.parseDouble(q1);
}
else{
Q1=Double.parseDouble(q1);
}
}
if(s.charAt(pos)!=','){
System.out.println("Wrong Format");
return;
}
pos++;
if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'||(s.charAt(pos)>='0'&&s.charAt(pos)<='9')){
t=pos;
if(s.charAt(pos)=='+'||s.charAt(pos)=='-'){
pos++;
}
if(s.charAt(pos)<'0'||s.charAt(pos)>'9'){
System.out.println("Wrong Format");
return;
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
q2+=s.charAt(pos);
pos++;
}
if(pos<len){
if(s.charAt(pos)=='.'){
q2+=".";
}
else if(s.charAt(pos)!=' '){
System.out.println("Wrong Format");
return;
}
if(s.charAt(pos)=='.'&&pos<len-1){
pos++;
if(s.charAt(pos)<'0'||s.charAt(pos)>'9'){
System.out.println("Wrong Format");
return;
}
}
while(pos<len&&s.charAt(pos)>='0'&&s.charAt(pos)<='9'){
q2+=s.charAt(pos);
pos++;
}
if(s.charAt(t)=='-'){
Q2=-Double.parseDouble(q2);
}
else{
Q2=Double.parseDouble(q2);
}
}
else{
if(s.charAt(t)=='-'){
Q2=-Double.parseDouble(q2);
}
else{
Q2=Double.parseDouble(q2);
}
}
}
if(len>pos){
System.out.print("wrong number of points");
return;
}
double res=Math.sqrt((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2));//计算两点距离
System.out.println(res);
}
}
sourcemonitor分析
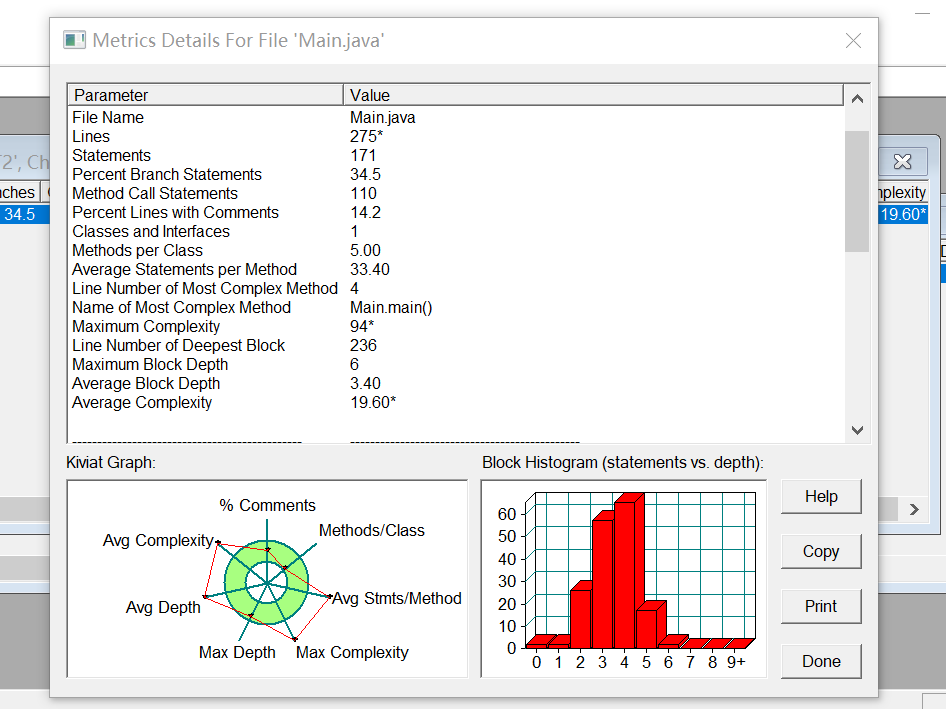
从sourcemonitor的源码分析来看,本题代码类的使用极少,每一个函数包含的语句多,最大圈复杂度高,平均圈复杂度高,代码质量欠佳。由于写这题时尚未掌握正则表达式的用法,代码实现过程中使用大量if-else,while等高复杂度语句对输入格式进行判断。
总结:在未掌握正则输入法的情况下写的本题。虽然答案正确,但代码冗余度极高,代码质量极低,且不便于他人理解。使用正则表达式后可将代码缩短至40~50行甚至更短,同时使代码更加清晰易懂。
第三次大作业T2
题面
用户输入一组选项和数据,进行与直线有关的计算。选项包括:
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
例如:1:0,0 1,1
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
不论哪个选项,如果格式、点数量都符合要求,但构成任一条线的两个点坐标重合,输出"points coincide",
输出格式:
见题目描述。
输入样例1:
选项1,两点重合。例如:
1:-2,+5 -2,+5
输出样例:
在这里给出相应的输出。例如:
points coincide
选项1,斜率无穷大的线。例如:
1:-2,3 -2,+5
在这里给出相应的输出。例如:
Slope does not exist
代码
import java.util.*;
public class Main{
static Double P1=0.0,P2=0.0,Q1=0.0,Q2=0.0,R1=0.0,R2=0.0,T1=0.0,T2=0.0;
public static void main(String[] args){
Scanner bjsn=new Scanner(System.in);
String s=bjsn.nextLine();
int len=s.length();
int cnt=0;
//基本格式判断
for(int i=0;i<len;i++){
if(s.charAt(i)==','){
cnt++;
}
}
if(cnt==0){
System.out.println("Wrong Format");
return;
}
if(s.charAt(0)<'1'||s.charAt(0)>'5'||s.charAt(1)!=':'){
System.out.println("Wrong Format");
return;
}
int pos=2,t=0;
if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
String p1="",p2="",q1="",q2="";
String sss=s.substring(2,len);
String ss[]=sss.split(" ");
String str[]=null;
for(String Str:ss){//正则输入法判断格式并提取数字
str=Str.split(",");
for(String tt:str){
if(!tt.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
System.out.println("Wrong Format");
return;
}
}
}
switch(s.charAt(0)){
case '1':if(ss.length!=2){//点数判断
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");//提取坐标
P1=Double.valueOf(str[0]);
P2=Double.valueOf(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
if(P1-Q1==0&&P2-Q2==0){//判断两点是否重合
System.out.println("points coincide");
}
else if(P1-Q1==0){//判断斜率是否存在
System.out.println("Slope does not exist");
}
else{//计算斜率
double res=(Q2-P2)/(Q1-P1);
System.out.println(res);
}
break;
case '2':if(ss.length!=3){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
if((P1-Q1==0&&P2-Q2==0)||(P1-R1==0&&P2-R2==0)||(R1-Q1==0&&R2-Q2==0)){//判断重点
System.out.println("points coincide");
return;
}
double res=0.0;
if(Q1-R1==0){//直线与x轴垂直
res=Math.abs(P1-Q1);
}
else{//公式计算
double k=(Q2-R2)/(Q1-R1);
double b=Q2-k*Q1;
res=Math.abs(k*P1-P2+b)/Math.sqrt(k*k+1);
}
System.out.println(res);
break;
case '3':if(ss.length!=3){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
if((P1-Q1==0&&P2-Q2==0)||(P1-R1==0&&P2-R2==0)||(R1-Q1==0&&R2-Q2==0)){
System.out.println("points coincide");
return;
}
if((P2-Q2)*(Q1-R1)==(P1-Q1)*(Q2-R2)){
System.out.println("true");
}
else{
System.out.println("false");
}
break;
case '4':if(ss.length!=4){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
str=ss[3].split(",");
T1=Double.parseDouble(str[0]);
T2=Double.parseDouble(str[1]);
if((P1-Q1==0&&P2-Q2==0)||(T1-R1==0&&T2-R2==0)){
System.out.println("points coincide");
return;
}
if(P1-Q1==0&&R1-T1==0){//两边均垂直于x轴
System.out.println("true");
}
else if(P1-Q1==0||R1-T1==0){
System.out.println("false");
}
else{//判断两边是否平行
if((P2-Q2)*(T1-R1)==(P1-Q1)*(T2-R2)){
System.out.println("true");
}
else{
System.out.println("false");
}
}
break;
case '5':if(ss.length!=4){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
str=ss[3].split(",");
T1=Double.parseDouble(str[0]);
T2=Double.parseDouble(str[1]);
boolean flag=true;
if((P1-Q1==0&&P2-Q2==0)||(T1-R1==0&&T2-R2==0)){
System.out.println("points coincide");
return;
}
if(P1-Q1==0&&R1-T1==0){
System.out.println("is parallel lines,have no intersection point");
flag=false;
}
else if(P1-Q1==0||R1-T1==0){//任意一边垂直于x轴
if(P1-Q1==0){
double k=(R2-T2)/(R1-T1);//求直线解析式
double b=T2-k*T1;
double y=k*P1+b;
double minx=Math.min(T1,R1);//求出交点坐标在线段上时应该满足的条件
double maxx=Math.max(T1,R1);
double miny=Math.min(P2,Q2);
double maxy=Math.max(P2,Q2);
if((P1<maxx&&P1>minx)||(y<maxy&&y>miny)){
System.out.println(P1+","+y+" true");
}
else{
System.out.println(P1+","+y+" false");
}
}
else{
double k=(P2-Q2)/(P1-Q1);
double b=Q2-k*Q1;
double y=k*R1+b;
double minx=Math.min(P1,Q1);
double maxx=Math.max(P1,Q1);
double miny=Math.min(R2,T2);
double maxy=Math.max(R2,T2);
if((R1<maxx&&R1>minx)||(y<maxy&&y>miny)){
System.out.println(R1+","+y+" true");
}
else{
System.out.println(R1+","+y+" false");
}
}
}
else{//公式求解
if((P2-Q2)*(T1-R1)==(P1-Q1)*(T2-R2)){//两直线平行
System.out.println("is parallel lines,have no intersection point");
}
else{
double minx1=Math.min(T1,R1);
double maxx1=Math.max(T1,R1);
double minx2=Math.min(P1,Q1);
double maxx2=Math.max(P1,Q1);
double a1=P2-Q2;
double b1=Q1-P1;
double c1=P1*Q2-P2*Q1;
double a2=R2-T2;
double b2=T1-R1;
double c2=R1*T2-R2*T1;
double d=a1*b2-a2*b1;
double x=(b1*c2-b2*c1)/d;
double y=(a2*c1-a1*c2)/d;
if((x<maxx1&&x>minx1)||(x<maxx2&&x>minx2)){
System.out.println(x+","+y+" true");
}
else{
System.out.println(x+","+y+" false");
}
}
}
break;
}
}
}
sourcemonitor分析

从sourcemonitor源码分析来看,方法的调用数量相比前两题略有提升,由于缺少类的使用,代码最大圈复杂度、平均圈复杂度依然居高不下。
总结:本题为第三次作业T1(即上一题)的升级版。在写本题时,曾用上一题的输入格式判断方法,结果使得代码长度超限。换用正则表达式判断后,代码简洁不少,且提取点的出错率下降很多。上一题判断边是否平行、计算两条直线交点的思路及公式可在本题使用。
第三次大作业T3
题面
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
如果输入的三个点无法构成三角形,输出"data error"。
注意:输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合,输出"points coincide",
输入样例1:
选项4,定义线的两点重合。例如:
4:1,0 1,0 0,0 2,0 4,0
输出样例:
在这里给出相应的输出。例如:
points coincide
输入样例2:
选项4,构成三角形的三个点在一条线上,无法构成三角形。例如:
4:1,0 0,2 0,0 0,0 4,0
输出样例:
在这里给出相应的输出。例如:
data error
代码
import java.util.*;
import java.text.DecimalFormat;
import java.io.*;
import java.lang.*;
import java.math.*;
import java.net.*;
import java.text.*;
import java.text.NumberFormat;
public class Main{
static double P1=0,P2=0,Q1=0,Q2=0,R1=0,R2=0,T1=0,T2=0,S1=0,S2=0;
public static void main(String[] args){
Scanner bjsn=new Scanner(System.in);
String s=bjsn.nextLine();
int len=s.length();
//基本格式判断
if(s.charAt(0)<'1'||s.charAt(0)>'5'||s.charAt(1)!=':'){
System.out.println("Wrong Format");
return;
}
int cnt=0;
for(int i=0;i<len;i++){
if(s.charAt(i)==','){
cnt++;
}
}
if(cnt==0){
System.out.println("Wrong Format");
return;
}
int pos=2,t=0;
if((s.charAt(pos)!='+'&&s.charAt(pos)!='-')&&(s.charAt(pos)<'0'||s.charAt(pos)>'9')){
System.out.println("Wrong Format");
return;
}
String sss=s.substring(2,len);
String ss[]=sss.split(" ");
String str[]=null;
for(String Str:ss){//正则表达式判断输入格式并提取数字
str=Str.split(",");
for(String tt:str){
if(!tt.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
System.out.println("Wrong Format");
return;
}
}
}
switch(s.charAt(0)){
case '1':if(ss.length!=3){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
if((P2-Q2)*(Q1-R1)==(P1-Q1)*(Q2-R2)){
System.out.println("data error");
return;
}
if((P1-Q1==0&&P2-Q2==0)||(P1-R1==0&&P2-R2==0)||(R1-Q1==0&&R2-Q2==0)){
System.out.println("points coincide");
return;
}
double a=Math.sqrt((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2));
double b=Math.sqrt((P1-R1)*(P1-R1)+(P2-R2)*(P2-R2));
double c=Math.sqrt((R1-Q1)*(R1-Q1)+(R2-Q2)*(R2-Q2));
boolean flag1=false,flag2=false;
if(a==b||b==c||a==c){//等腰三角形的判断
flag1=true;
}
if(a==b&&b==c){//等边三角形的判断
flag2=true;
}
if(flag1&&flag2){
System.out.println("true true");
}
else if(flag1){
System.out.println("true false");
}
else{
System.out.println("false false");
}
break;
case '2':if(ss.length!=3){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
double p1=Double.parseDouble(str[0]);
double p2=Double.parseDouble(str[1]);
str=ss[1].split(",");
double q1=Double.parseDouble(str[0]);
double q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
double r1=Double.parseDouble(str[0]);
double r2=Double.parseDouble(str[1]);
if((p2-q2)*(q1-r1)==(p1-q1)*(q2-r2)){
System.out.println("data error");
return;
}
if((p1-q1==0&&p2-q2==0)||(p1-r1==0&&p2-r2==0)||(r1-q1==0&&r2-q2==0)){
System.out.println("points coincide");
return;
}
a=Math.sqrt((p1-q1)*(p1-q1)+(p2-q2)*(p2-q2));
b=Math.sqrt((p1-r1)*(p1-r1)+(p2-r2)*(p2-r2));
c=Math.sqrt((r1-q1)*(r1-q1)+(r2-q2)*(r2-q2));
double C=a+b+c;//计算周长
BigDecimal Cc=new BigDecimal(C);
double c0=Cc.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
double cosa=(b*b+c*c-a*a)/(2*b*c);
double sina=Math.sqrt(1-cosa*cosa);
double S=(b*c*sina/2);//计算面积
BigDecimal Ss=new BigDecimal(S);
double s0=Ss.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
double x=((p1+q1+r1)/3);//计算重心横坐标
BigDecimal Xx=new BigDecimal(x);
double x0=Xx.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
double y=((p2+q2+r2)/3);//计算重心纵坐标
BigDecimal Yy=new BigDecimal(y);
double y0=Yy.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println(c0+" "+s0+" "+x0+","+y0);//格式输出
break;
case '3':if(ss.length!=3){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
if((P2-Q2)*(Q1-R1)==(P1-Q1)*(Q2-R2)){
System.out.println("data error");
return;
}
if((P1-Q1==0&&P2-Q2==0)||(P1-R1==0&&P2-R2==0)||(R1-Q1==0&&R2-Q2==0)){
System.out.println("points coincide");
return;
}
a=Math.sqrt((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2));
b=Math.sqrt((P1-R1)*(P1-R1)+(P2-R2)*(P2-R2));
c=Math.sqrt((R1-Q1)*(R1-Q1)+(R2-Q2)*(R2-Q2));
boolean f1=false,f2=false,f3=false;
if(((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2)==(P1-R1)*(P1-R1)+(P2-R2)*(P2-R2)+(R1-Q1)*(R1-Q1)+(R2-Q2)*(R2-Q2))||((P1-R1)*(P1-R1)+(P2-R2)*(P2-R2)==(P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2)+(R1-Q1)*(R1-Q1)+(R2-Q2)*(R2-Q2))||((R1-Q1)*(R1-Q1)+(R2-Q2)*(R2-Q2)==(P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2)+(P1-R1)*(P1-R1)+(P2-R2)*(P2-R2))){
f2=true;//直角三角形的判断
}
else{
cosa=(b*b+c*c-a*a)/(2*b*c);
double cosb=(a*a+c*c-b*b)/(2*a*c);
double cosc=(a*a+b*b-c*c)/(2*a*b);
if(cosa<0||cosb<0||cosc<0){//任意一角余弦值小于0,为钝角
f3=true;
}
else{
f1=true;
}
}
if(f1){
System.out.println("false false true");
}
else if(f2){
System.out.println("false true false");
}
else{
System.out.println("true false false");
}
break;
case '4':if(ss.length!=5){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
str=ss[3].split(",");
T1=Double.parseDouble(str[0]);
T2=Double.parseDouble(str[1]);
str=ss[4].split(",");
S1=Double.parseDouble(str[0]);
S2=Double.parseDouble(str[1]);
if((P1-Q1==0&&P2-Q2==0)){
System.out.println("points coincide");
return;
}
if((R2-S2)*(S1-T1)==(R1-S1)*(S2-T2)){
System.out.println("data error");
return;
}
a=Math.sqrt((S1-T1)*(S1-T1)+(S2-T2)*(S2-T2));
b=Math.sqrt((T1-R1)*(T1-R1)+(T2-R2)*(T2-R2));
c=Math.sqrt((R1-S1)*(R1-S1)+(R2-S2)*(R2-S2));
double p0=(a+b+c)/2;
S=Math.sqrt(p0*(p0-a)*(p0-b)*(p0-c));
double minx=Math.min(R1,Math.min(S1,T1));
double maxx=Math.max(R1,Math.max(S1,T1));
if(P1-Q1==0){
if(P1==minx||P1==maxx){
if((R1==T1&&R1==P1)||(R1==S1&&P1==R1)||(S1==T1&&T1==R1)){
System.out.println("The point is on the edge of the triangle");
}
else{
System.out.println("1");
}
return;
}
else if(P1<minx||P1>maxx){//无交点
System.out.println("0");
return;
}
else{
if(R1==S1){//与x轴垂直
double fz=Math.abs(T1-P1);
double fm=Math.abs(T1-R1);
double frac=(fz/fm)*(fz/fm);//求比例
double sl=S*frac;
double sr=S-sl;
if(sl>sr){
double temp=sl;
sl=sr;
sr=temp;
}
BigDecimal Sl=new BigDecimal(sl);
sl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(sr);
sr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+sl+" "+sr);
}
else if(R1==T1){
double fz=Math.abs(S1-P1);
double fm=Math.abs(S1-R1);
double frac=(fz/fm)*(fz/fm);
double sl=S*frac;
double sr=S-sl;
if(sl>sr){
double temp=sl;
sl=sr;
sr=temp;
}
BigDecimal Sl=new BigDecimal(sl);
sl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(sr);
sr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+sl+" "+sr);
}
else if(T1==S1){
double fz=Math.abs(R1-P1);
double fm=Math.abs(T1-R1);
double frac=(fz/fm)*(fz/fm);
double sl=S*frac;
double sr=S-sl;
if(sl>sr){
double temp=sl;
sl=sr;
sr=temp;
}
BigDecimal Sl=new BigDecimal(sl);
sl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(sr);
sr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+sl+" "+sr);
}
}
}
else{//直线不与x轴垂直
double ssl,ssr;
double Apq=Q2-P2;
double Bpq=P1-Q1;
double Cpq=Q1*P2-Q2*P1;
double Ars=R2-S2;
double Brs=S1-R1;
double Crs=R1*S2-R2*S1;
double Art=R2-T2;
double Brt=T1-R1;
double Crt=R1*T2-R2*T1;
double Ast=T2-S2;
double Bst=S1-T1;
double Cst=T1*S2-T2*S1;
double d1=Apq*Brs-Ars*Bpq;
double d2=Apq*Brt-Art*Bpq;
double d3=Apq*Bst-Ast*Bpq;
if(d1==0||d2==0||d3==0){//直线与三角形任意边平行
if(d1==0){
if(Apq*R1+Bpq*R2+Cpq==0){
System.out.println("The point is on the edge of the triangle");
return;
}
if((Apq*R1+Bpq*R2+Cpq<0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*T1+Bpq*T2+Cpq>0)){
System.out.println("0");
return;
}
if(Apq*T1+Bpq*T2+Cpq==0){
System.out.println("1");
return;
}
double xt=(Bpq*Cst-Bst*Cpq)/d3;
double yt=(Ast*Cpq-Apq*Cst)/d3;
double dis1=Math.sqrt((xt-T1)*(xt-T1)+(yt-T2)*(yt-T2));
double ff1=(dis1/a)*(dis1/a);//求分割出的小三角形比例
ssl=S*ff1;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else if(d2==0){
if(Apq*R1+Bpq*R2+Cpq==0){
System.out.println("The point is on the edge of the triangle");
return;
}
if((Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq>0)){
System.out.println("0");
return;
}
if(Apq*S1+Bpq*S2+Cpq==0){
System.out.println("1");
return;
}
double xt=(Bpq*Cst-Bst*Cpq)/d3;
double yt=(Ast*Cpq-Apq*Cst)/d3;
double dis1=Math.sqrt((xt-S1)*(xt-S1)+(yt-S2)*(yt-S2));
double ff1=(dis1/a)*(dis1/a);
ssl=S*ff1;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else{
if(Apq*S1+Bpq*S2+Cpq==0){
System.out.println("The point is on the edge of the triangle");
return;
}
if((Apq*R1+Bpq*R2+Cpq<0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*T1+Bpq*T2+Cpq>0)){
System.out.println("0");
return;
}
if(Apq*R1+Bpq*R2+Cpq==0){
System.out.println("1");
return;
}
double xt=(Bpq*Crt-Brt*Cpq)/d2;
double yt=(Art*Cpq-Apq*Crt)/d2;
double dis1=Math.sqrt((xt-R1)*(xt-R1)+(yt-R2)*(yt-R2));
double ff1=(dis1/b)*(dis1/b);
ssl=S*ff1;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
}
else{//直线与三角形任意一边均不平行
if((Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq<0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq>0&&Apq*T1+Bpq*T2+Cpq>0)){
System.out.println("0");
return;
}
if((Apq*R1+Bpq*R2+Cpq==0&&Apq*S1+Bpq*S2+Cpq<0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq==0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq<0&&Apq*T1+Bpq*T2+Cpq==0)||(Apq*R1+Bpq*R2+Cpq==0&&Apq*S1+Bpq*S2+Cpq>0&&Apq*T1+Bpq*T2+Cpq>0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq==0&&Apq*T1+Bpq*T2+Cpq>0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq>0&&Apq*T1+Bpq*T2+Cpq==0)){
System.out.println("1");
return;
}
if(Apq*R1+Bpq*R2+Cpq==0){//与三角形顶点R相交
double xt=(Bpq*Cst-Bst*Cpq)/d3;
double yt=(Ast*Cpq-Apq*Cst)/d3;
double dis1=Math.sqrt((xt-T1)*(xt-T1)+(yt-T2)*(yt-T2));
double ff1=dis1/a;
ssl=ff1*S;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else if(Apq*T1+Bpq*T2+Cpq==0){//与三角形顶点T相交
double xt=(Bpq*Crs-Brs*Cpq)/d1;
double yt=(Ars*Cpq-Apq*Crs)/d1;
double dis1=Math.sqrt((xt-R1)*(xt-R1)+(yt-R2)*(yt-R2));
double ff1=dis1/c;
ssl=ff1*S;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else if(Apq*S1+Bpq*S2+Cpq==0){//与三角形顶点S相交
double xt=(Bpq*Crt-Brt*Cpq)/d2;
double yt=(Art*Cpq-Apq*Crt)/d2;
double dis1=Math.sqrt((xt-T1)*(xt-T1)+(yt-T2)*(yt-T2));
double ff1=dis1/b;
ssl=ff1*S;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else{//与三角形任意两边相交,找出切分出来的小三角形
if((Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq<0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq>0&&Apq*T1+Bpq*T2+Cpq>0)){
double xt=(Bpq*Crs-Brs*Cpq)/d1;
double yt=(Ars*Cpq-Apq*Crs)/d1;
double dis1=Math.sqrt((xt-R1)*(xt-R1)+(yt-R2)*(yt-R2));
double xm=(Bpq*Crt-Brt*Cpq)/d2;
double ym=(Art*Cpq-Apq*Crt)/d2;
double dis2=Math.sqrt((xm-R1)*(xm-R1)+(ym-R2)*(ym-R2));
double ff=dis1*dis2/(b*c);
ssl=ff*S;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else if((Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq>0&&Apq*T1+Bpq*T2+Cpq<0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq<0&&Apq*T1+Bpq*T2+Cpq>0)){//剩余情况均为直线一边有一点,另一边有两点,找出一个点那一端,求小三角形的面积
double xt=(Bpq*Crs-Brs*Cpq)/d1;
double yt=(Ars*Cpq-Apq*Crs)/d1;
double dis1=Math.sqrt((xt-S1)*(xt-S1)+(yt-S2)*(yt-S2));
double xm=(Bpq*Cst-Bst*Cpq)/d2;
double ym=(Ast*Cpq-Apq*Cst)/d2;
double dis2=Math.sqrt((xm-S1)*(xm-S1)+(ym-S2)*(ym-S2));
double ff=dis1*dis2/(a*c);
ssl=ff*S;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
else if((Apq*R1+Bpq*R2+Cpq<0&&Apq*S1+Bpq*S2+Cpq<0&&Apq*T1+Bpq*T2+Cpq>0)||(Apq*R1+Bpq*R2+Cpq>0&&Apq*S1+Bpq*S2+Cpq>0&&Apq*T1+Bpq*T2+Cpq<0)){
double xt=(Bpq*Crt-Brt*Cpq)/d2;
double yt=(Art*Cpq-Apq*Crt)/d2;
double dis1=Math.sqrt((xt-T1)*(xt-T1)+(yt-T2)*(yt-T2));
double xm=(Bpq*Cst-Bst*Cpq)/d3;
double ym=(Ast*Cpq-Apq*Cst)/d3;
double dis2=Math.sqrt((xm-T1)*(xm-T1)+(ym-T2)*(ym-T2));
double ff=dis1*dis2/(a*b);
ssl=ff*S;
ssr=S-ssl;
double SL=Math.min(ssl,ssr);
double SR=Math.max(ssl,ssr);
BigDecimal Sl=new BigDecimal(SL);
ssl=Sl.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
BigDecimal Sr=new BigDecimal(SR);
ssr=Sr.setScale(6,BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("2"+" "+ssl+" "+ssr);
}
}
}
}
break;
case '5':if(ss.length!=4){
if(cnt!=ss.length)
System.out.println("Wrong Format");
else
System.out.println("wrong number of points");
return;
}
str=ss[0].split(",");
P1=Double.parseDouble(str[0]);
P2=Double.parseDouble(str[1]);
str=ss[1].split(",");
Q1=Double.parseDouble(str[0]);
Q2=Double.parseDouble(str[1]);
str=ss[2].split(",");
R1=Double.parseDouble(str[0]);
R2=Double.parseDouble(str[1]);
str=ss[3].split(",");
T1=Double.parseDouble(str[0]);
T2=Double.parseDouble(str[1]);
if((T2-Q2)*(Q1-R1)==(T1-Q1)*(Q2-R2)){
System.out.println("data error");
return;
}
if((R1-T1==0&&R2-T2==0)||(R1-Q1==0&&R2-Q2==0)||(Q1-T1==0&&Q2-T2==0)){
System.out.println("points coincide");
return;
}
//用海伦-秦九韶法计算三角形面积
a=Math.sqrt((T1-R1)*(T1-R1)+(T2-R2)*(T2-R2));
b=Math.sqrt((T1-Q1)*(T1-Q1)+(T2-Q2)*(T2-Q2));
c=Math.sqrt((R1-Q1)*(R1-Q1)+(R2-Q2)*(R2-Q2));
double p=(a+b+c)/2;
S=Math.sqrt(p*(p-a)*(p-b)*(p-c));
double Pq=Math.sqrt((P1-Q1)*(P1-Q1)+(P2-Q2)*(P2-Q2));
double Pr=Math.sqrt((P1-R1)*(P1-R1)+(P2-R2)*(P2-R2));
double Ps=Math.sqrt((P1-T1)*(P1-T1)+(P2-T2)*(P2-T2));
double pq=(a+Pr+Ps)/2;
double pr=(b+Pq+Ps)/2;
double ps=(c+Pq+Pr)/2;
double Sa=Math.sqrt(Math.abs(pq*(pq-a)*(pq-Pr)*(pq-Ps)));
double Sb=Math.sqrt(Math.abs(pr*(pr-Pq)*(pr-b)*(pr-Ps)));
double Sc=Math.sqrt(Math.abs(ps*(ps-Pq)*(ps-Pr)*(ps-c)));
if(Sa==0||Sb==0||Sc==0){
System.out.println("on the triangle");
}
else if(Math.abs(Sa+Sb+Sc-S)<0.0000001){
System.out.println("in the triangle");
}
else{
System.out.println("outof the triangle");
}
break;
}
}
}
sourcemonitor分析
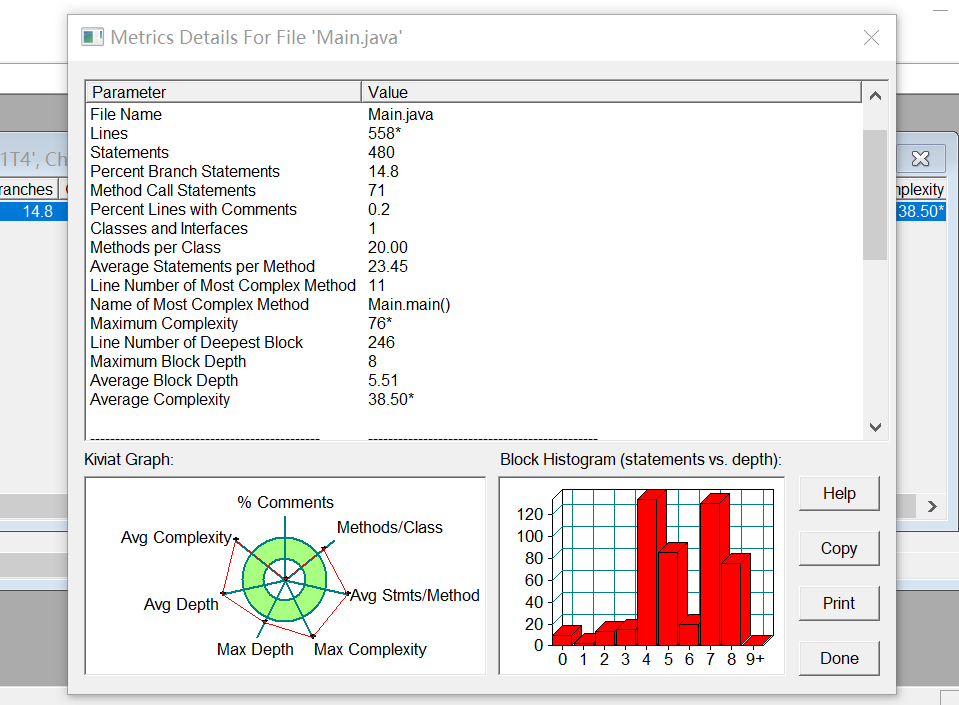
从sourcemonitor的源码分析来看,方法、平均深度比前三道题更大,代码的圈复杂度依然较高,代码质量欠佳。
总结:本题为本篇博客所分析的四道题中最复杂的一题,同时也是第三次作业前两道题的升级版,实现难度、细节考查相比前两道题有了较大提升。但是把这道题计算所需要的量都列出来,再逐个使用,能使思路清晰不少。
三、踩坑心得
1.作为严谨性高的编程语言,java编程过程中有许多限制。不同类型的变量在转换时需要用到强制类型转换等手段使得类型统一。表示字符串s中第i个字符时,不同于C/C++的s[i],java编程时要写成s.charAt(i)等形式。给初学java的程序设计者最直观的感受就是复杂、不便理解、看到报错却怎么都找不出哪里错了搞心态。编写java程序时需理清楚要做什么。
2.精度问题。double和float类型变量在计算过程中可能出现炸精度的现象,计算出的结果与理论结果存在偏差,这点在计算斜率、交点,以及线长时尤为常见。判断两直线是否平行时时可将斜率表达式改为两边相乘的形式,尽量避免除法的使用;同时也可将x==0改为Math.abs(x)<0.0000001来避免此类情况的出现。
3.正则表达式判断输入是否正确并提取数字。在第三次作业T1中,我为了判断并提取数字,写了大量代码实现,造成了极大的时间浪费,还使得代码过度冗余,不便阅读以及理解。
4.注意java自带函数的使用。提取字符串s中第i位字符时,需要写成s.charAt(i)的形式。如在输出最多几位数时,需用到java自带的BigDecimal、setScale函数。
四、改进建议
1.写java代码时多用类。与其辛辛苦苦多写几百行代码,不如先写好类和函数然后调用。
2.重视正则表达式的学习使用。为了判断一个输入格式,一个正则表达式判断就解决的问题,写那么多代码作甚。
五、总结
通过这三次作业的练习,我java基本语法算是入门了。然而,我目前对java最重要的思想——面向对象,还处于一知半解的状态,对于类的使用依然不太习惯。仅仅只追求所有题目拿到满分,只会让自己的java学习浅尝辄止。以后还需多学习java的更多不同语法语句的用法,能掌握就尽量掌握;多看看编程大佬的代码,学习怎样让自己的代码更简洁、思路更清晰。锲而舍之,朽木不折;锲而不舍,金石可镂。最后感谢老师和同学对我学习java过程中提供的帮助!


