信息安全(一)-编码算法【base64编码、base58编码】、哈希算法【MD、sha、RipeMD-XX、hamc】
代码地址:https://github.com/bjlhx15/algorithm-sign.git
一、java版本概述
主要实现源
a、jdk原生实现
b、bouncycastle:一个提供了很多哈希算法和加密算法的第三方库。它提供了Java标准库没有的一些算法,例如,RipeMD160哈希算法
<dependency>
<groupId>org.bouncycastle</groupId>
<artifactId>bcprov-jdk15on</artifactId>
<version>1.58</version>
</dependency>
使用如下即可

public class Main { public static void main(String[] args) throws Exception { // 注册BouncyCastle: Security.addProvider(new BouncyCastleProvider()); // 按名称正常调用: MessageDigest md = MessageDigest.getInstance("RipeMD160"); md.update("HelloWorld".getBytes("UTF-8")); byte[] result = md.digest(); System.out.println(new BigInteger(1, result).toString(16)); } }
二、算法实现
- MD5(Message Digest algorithm 5,信息摘要算法)
- SHA(Secure Hash Algorithm,安全散列算法)
- HMAC(Hash Message Authentication Code,散列消息鉴别码)
- RIPEMD(RACE Integrity Primitives Evaluation Message Digest,RACE原始完整性校验消息摘要)
注意点一、哈希算法(Hash)
又称摘要算法(Digest),它的作用是:对任意一组输入数据进行计算,得到一个固定长度的输出摘要。其实就是一个哈希函数。
哈希函数,又称散列算法,是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。该函数将数据打乱混合,重新创建一个叫做散列值(或哈希值)的指纹。散列值通常用一个短的随机字母和数字组成的字符串来代表。
哈希算法最重要的特点就是:
-
- 相同的输入一定得到相同的输出;
- 不同的输入大概率得到不同的输出。
哈希算法的目的就是为了验证原始数据是否被篡改。
Java字符串的hashCode()就是一个哈希算法,它的输入是任意字符串,输出是固定的4字节int整数:
"hello".hashCode(); // 0x5e918d2 "hello, java".hashCode(); // 0x7a9d88e8
两个相同的字符串永远会计算出相同的hashCode,否则基于hashCode定位的HashMap就无法正常工作。这也是为什么当我们自定义一个class时,覆写equals()方法时我们必须正确覆写hashCode()方法。
注意点二、哈希碰撞
哈希碰撞是指,两个不同的输入得到了相同的输出:
System.out.println("AaAaAa".hashCode());//1952508096
System.out.println("BBAaBB".hashCode());//1952508096
碰撞是一定会出现的,因为输出的字节长度是固定的,String的hashCode()输出是4字节整数,最多只有4294967296种输出,但输入的数据长度是不固定的,有无数种输入。所以,哈希算法是把一个无限的输入集合映射到一个有限的输出集合,必然会产生碰撞。
碰撞不避免,但是降低碰撞的概率,因为碰撞概率的高低关系到哈希算法的安全性。一个安全的哈希算法必须满足:
-
- 碰撞概率低;
- 不能猜测输出。
根据碰撞概率,哈希算法的输出长度越长,就越难产生碰撞,也就越安全。
2.1、编码算法-Base64编码
按照RFC2045的定义,Base64被定义为:Base64内容传送编码被设计用来把任意序列的8位字节描述为一种不易被人直接识别的形式。(The Base64 Content-Transfer-Encoding is designed to represent arbitrary sequences of octets in a form that need not be humanly readable.) 传输8Bit字节代码的编码方式之一。
Base64是一种任意二进制到文本字符串的编码方法,常用于在URL、Cookie、网页中传输少量二进制数据。不是加密算法,只是无法直接看到明文。可以通过打乱Base64编码来进行加密。
等号“=”作用:Base64编码的长度永远是4的倍数,因此,需要加上=把Base64字符串的长度变为4的倍数
规则:①.把3个字节变成4个字节。②每76个字符加一个换行符。③.最后的结束符也要处理。
中文有多种编码(比如:utf-8、gb2312、gbk等),不同编码对应Base64编码结果都不一样。
2.1.1、实现方式
1、jdk1.8以前【不推荐】
性能低
2、jdk1.8【推荐】
3、使用:commons.codec
<dependency>
<groupId>commons-codec</groupId>
<artifactId>commons-codec</artifactId>
<version>1.11</version>
</dependency>
2.1.2、原理
1、标准的Base64协议规定索引表
['A', 'B', 'C', ... 'a', 'b', 'c', ... '0', '1', ... '+', '/']
Base64的索引表,字符选用了"A-Z、a-z、0-9、+、/" 64个可打印字符
2、转换步骤
第一步,将待转换的字符串每三个字节分为一组,每个字节占8bit,那么共有24个二进制位。
第二步,将上面的24个二进制位每6个一组,共分为4组。
第三步,在每组前面添加两个0,每组由6个变为8个二进制位,总共32个二进制位,即四个字节。
第四步,根据Base64编码对照表(见下图)获得对应的值。
0 A 17 R 34 i 51 z 1 B 18 S 35 j 52 0 2 C 19 T 36 k 53 1 3 D 20 U 37 l 54 2 4 E 21 V 38 m 55 3 5 F 22 W 39 n 56 4 6 G 23 X 40 o 57 5 7 H 24 Y 41 p 58 6 8 I 25 Z 42 q 59 7 9 J 26 a 43 r 60 8 10 K 27 b 44 s 61 9 11 L 28 c 45 t 62 + 12 M 29 d 46 u 63 / 13 N 30 e 47 v 14 O 31 f 48 w 15 P 32 g 49 x 16 Q 33 h 50 y
从上面的步骤我们发现:
Base64字符表中的字符原本用6个bit就可以表示,现在前面添加2个0,变为8个bit,会造成一定的浪费。因此,Base64编码之后的文本,要比原文大约三分之一。
为什么使用3个字节一组呢?因为6和8的最小公倍数为24,三个字节正好24个二进制位,每6个bit位一组,恰好能够分为4组。
2.1.3、示例:man编码

第一步:“M”、“a”、"n"对应的ASCII码值分别为77,97,110,对应的二进制值是01001101、01100001、01101110。如图第二三行所示,由此组成一个24位的二进制字符串。
第二步:如图红色框,将24位每6位二进制位一组分成四组。
第三步:在上面每一组前面补两个0,扩展成32个二进制位,此时变为四个字节:00010011、00010110、00000101、00101110。分别对应的值(Base64编码索引)为:19、22、5、46。
第四步:用上面的值在Base64编码表中进行查找,分别对应:T、W、F、u。因此“Man”Base64编码之后就变为:TWFu。
2.1.4、补位【位数不是4的倍数】
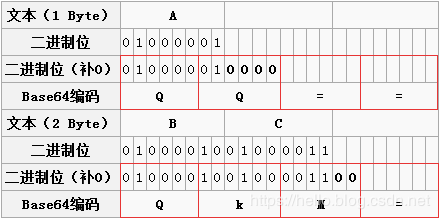
一个字节【A】:一个字节共8个二进制位,依旧按照规则进行分组。此时共8个二进制位,每6个一组,则第二组缺少4位,用0补齐,得到两个Base64编码,而后面两组没有对应数据,都用“=”补上。因此,上图中“A”转换之后为“QQ==”;
两个字节【BC】:两个字节共16个二进制位,依旧按照规则进行分组。此时总共16个二进制位,每6个一组,则第三组缺少2位,用0补齐,得到三个Base64编码,第四组完全没有数据则用“=”补上。因此,上图中“BC”转换之后为“QKM=”;
2.1.5、扩展
Base64就是用6位(2的6次幂就是64)表示字符,因此成为Base64,即每6个一组,有64个字符表示。同理,Base32就是用5位,Base16就是用4位。
1、为什么只能支持64个字符呢,多了不是更好吗?可打印字符又是什么意思?
ASCII码的范围是0-127,其中0-31和127这33个字符属于控制字符(Controlcharacters)。剩下32-126这95个字符属于可打印字符(Printable characters),包含数字、大小写字母、常用符号。
从这95个中又选择了26个大写,26个小写,10个数字,2个特殊符号【+ /】共64个。
早先的一些传输协议,例如传输邮件的SMTP协议,只能传输可打印的ASCII字符。导致原本8Bit的字节码(范围0-255)超过了可用的范围。比如当邮件传输图片资源的时候,某一个Byte值是10111011B,对应十进制187不属于ASCII码范围,因此无法被传输。这个时候,Base64编码应用而生了,它利用6bit字符表达了原本的8bit字符。Base64可以把原本ASCII码的控制字符甚至ASCII码之外的字符都转换成可打印的6big字符。
2.1.6、解码
6bit X 4的字符串可以每8bit分成一组,共3组。每一组转换成一个8位的Byte字节。
2.2、编码算法-Base58编码
Base58是用于Bitcoin中使用的一种独特的编码方式,主要用于产生Bitcoin的钱包地址。但是这个base58的计算量比base64的计算量多了很多。因为58不是2的整数倍,需要不断用除法去计算。
基于ALPHABET = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz"共计58个
通常base64编码一样,base58编码的作用也是将非可视字符可视化(ASCII化)。base58编码去掉了几个看起来会产生歧义的字符,如 0 (零), O (大写字母O), I (大写的字母i) and l (小写的字母L) ,和几个影响双击选择的字符,如/, +。
结果字符集正好58个字符(包括9个数字,24个大写字母,25个小写字母)。而且因为58 不是2的整次幂,所以没有使用类似base64编码中使用直接截取3个字符转4个字符(3*8=4*6 , 2的6次方刚好64)的方法进行转换,而是采用我们数学上经常使用的进制转换方法——辗转相除法(本质上,base64编码是64进制,base58是58进制)。看下base58的编码表:
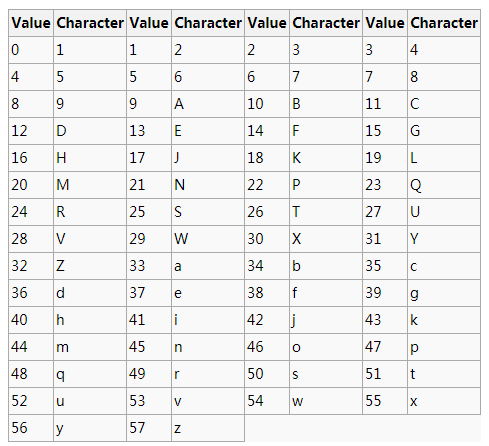
也就是字符1代表0,字符2代表1,字符3代表2...字符z代表57。然后回一下辗转相除法。
如要将1234转换为58进制;
第一步:1234除于58,商21,余数为16,查表得H
第二步:21除于58,商0,余数为21,查表得N
所以得到base58编码为:NH
如果待转换的数前面有0怎么办?直接附加编码1来代表,有多少个就附加多少个(编码表中1代表0)。
暂时没有找到开源公共类,代码中有java实现
2.2.1、base 58 与 base 64 异同
相同:
1. 一般都用于URL, 邮件文本, 可见字符显示.
2. 都会造成信息冗余, 数据量增大, 因此不会用于大数据传输编码.
区别:
1. 编码集不同, base 58 的编码集在 base 64 的字符集的基础上去掉了比较容易混淆的字符.
2. base 64 采用直接切割 bit 的方法(8->6), 而 base 58 采用大数进制转换, 效率更低, 使用场景更少.
Note: base 58 解码时需要将长度传入, 这点与 base 64 有区别, 在代码实现时应注意.
2.3、哈希算法-MD【消息摘要】
Message Digest Algorithm MD5(中文名为消息摘要算法第五版)为计算机安全领域广泛使用的一种散列函数,用以提供消息的完整性保护。
MD5即Message-Digest Algorithm 5(信息-摘要算法5),用于确保信息传输完整一致。是计算机广泛使用的杂凑算法之一(又译摘要算法、哈希算法),主流编程语言普遍已有MD5实现。将数据(如汉字)运算为另一固定长度值,是杂凑算法的基础原理,MD5的前身有MD2、MD3和MD4。推荐使用MD5
| 算法 | 摘要长度 | 实现方 | |
| MD2 | 128 | jdk/bc | |
| MD4 | 128 | bc | |
| MD5 | 128 | jdk/bc |
2.3.1、原理
MD5以512位分组来处理输入的信息 ,且每一分组又被划分为16个 32位子分组,经过了一系列的处理后 ,算法的输出由四个32位分组组成,将这四个32位分组级联后将生成一个128位散列值。
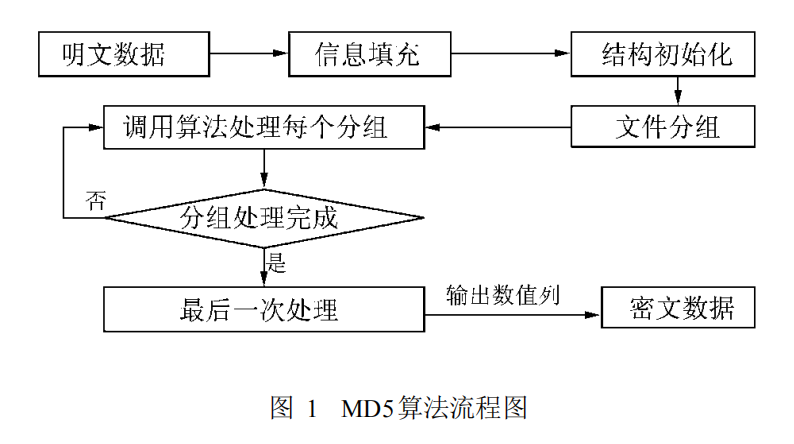
1、数据填充
计算出原文长度(bit)对 512 求余的结果,如果不等于 448,就需要填充原文使得原文对 512 求余的结果等于 448;
填充的方法是第一位填充 1,其余位填充 0。填充完后,信息的长度就是 512*N+448。之后,用剩余的位置(512-448=64 位)记录原文的真正长度,把长度的二进制值补在最后。这样处理后的信息长度就是 512*(N+1)。
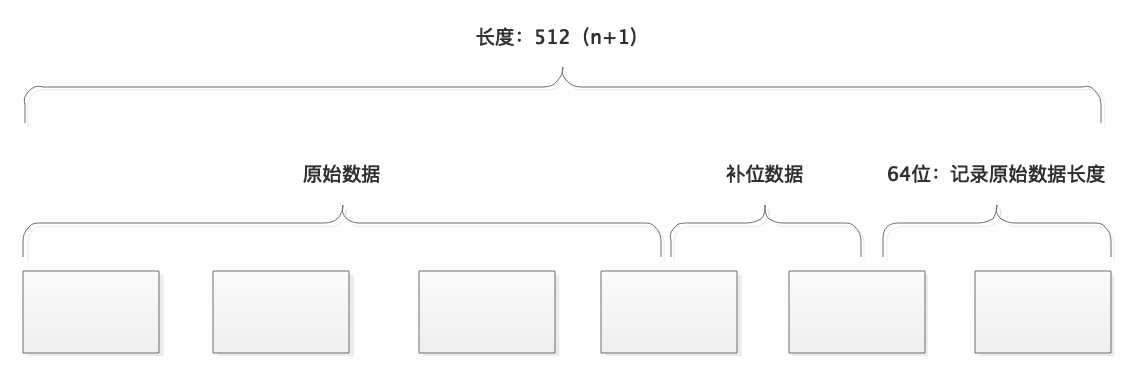
2、数据处理
1.首先将数据按每个512位为一组进行分组,每组里面分成16个32位,也就是16个long
四个常量:A = 0x01234567,B = 0x89abcdef, C = 0xfedcba98,D =0x76543210
四个基础线性函数
F(X,Y,Z) = (X & Y) | ((~X) & Z); G(X,Y,Z) = (X & Z) | (Y & (~Z)); H(X,Y,Z) = X ^ Y ^ Z; I(X,Y,Z) = Y ^ (X | (~Z)); (&是与,|是或,~是非,^是异或)
四个数据处理函数,Mj表示第M组第j个long数
FF(a,b,c,d,Mj,s,ti)表示a=b+((a+F(b,c,d)+Mj+ti)<<<s) GG(a,b,c,d,Mj,s,ti)表示a=b+((a+G(b,c,d)+Mj+ti)<<<s) HH(a,b,c,d,Mj,s,ti)表示a=b+((a+H(b,c,d)+Mj+ti)<<<s) II(a,b,c,d,Mj,s,ti)表示a=b+((a+I(b,c,d)+Mj+ti)<<<s)
2.对分组进行计算

第一轮 a=FF(a,b,c,d,M0,7,0xd76aa478) b=FF(d,a,b,c,M1,12,0xe8c7b756) c=FF(c,d,a,b,M2,17,0x242070db) d=FF(b,c,d,a,M3,22,0xc1bdceee) a=FF(a,b,c,d,M4,7,0xf57c0faf) b=FF(d,a,b,c,M5,12,0x4787c62a) c=FF(c,d,a,b,M6,17,0xa8304613) d=FF(b,c,d,a,M7,22,0xfd469501) a=FF(a,b,c,d,M8,7,0x698098d8) b=FF(d,a,b,c,M9,12,0x8b44f7af) c=FF(c,d,a,b,M10,17,0xffff5bb1) d=FF(b,c,d,a,M11,22,0x895cd7be) a=FF(a,b,c,d,M12,7,0x6b901122) b=FF(d,a,b,c,M13,12,0xfd987193) c=FF(c,d,a,b,M14,17,0xa679438e) d=FF(b,c,d,a,M15,22,0x49b40821) 第二轮 a=GG(a,b,c,d,M1,5,0xf61e2562) b=GG(d,a,b,c,M6,9,0xc040b340) c=GG(c,d,a,b,M11,14,0x265e5a51) d=GG(b,c,d,a,M0,20,0xe9b6c7aa) a=GG(a,b,c,d,M5,5,0xd62f105d) b=GG(d,a,b,c,M10,9,0x02441453) c=GG(c,d,a,b,M15,14,0xd8a1e681) d=GG(b,c,d,a,M4,20,0xe7d3fbc8) a=GG(a,b,c,d,M9,5,0x21e1cde6) b=GG(d,a,b,c,M14,9,0xc33707d6) c=GG(c,d,a,b,M3,14,0xf4d50d87) d=GG(b,c,d,a,M8,20,0x455a14ed) a=GG(a,b,c,d,M13,5,0xa9e3e905) b=GG(d,a,b,c,M2,9,0xfcefa3f8) c=GG(c,d,a,b,M7,14,0x676f02d9) d=GG(b,c,d,a,M12,20,0x8d2a4c8a) 第三轮 a=HH(a,b,c,d,M5,4,0xfffa3942) b=HH(d,a,b,c,M8,11,0x8771f681) c=HH(c,d,a,b,M11,16,0x6d9d6122) d=HH(b,c,d,a,M14,23,0xfde5380c) a=HH(a,b,c,d,M1,4,0xa4beea44) b=HH(d,a,b,c,M4,11,0x4bdecfa9) c=HH(c,d,a,b,M7,16,0xf6bb4b60) d=HH(b,c,d,a,M10,23,0xbebfbc70) a=HH(a,b,c,d,M13,4,0x289b7ec6) b=HH(d,a,b,c,M0,11,0xeaa127fa) c=HH(c,d,a,b,M3,16,0xd4ef3085) d=HH(b,c,d,a,M6,23,0x04881d05) a=HH(a,b,c,d,M9,4,0xd9d4d039) b=HH(d,a,b,c,M12,11,0xe6db99e5) c=HH(c,d,a,b,M15,16,0x1fa27cf8) d=HH(b,c,d,a,M2,23,0xc4ac5665) 第四轮 a=II(a,b,c,d,M0,6,0xf4292244) b=II(d,a,b,c,M7,10,0x432aff97) c=II(c,d,a,b,M14,15,0xab9423a7) d=II(b,c,d,a,M5,21,0xfc93a039) a=II(a,b,c,d,M12,6,0x655b59c3) b=II(d,a,b,c,M3,10,0x8f0ccc92) c=II(c,d,a,b,M10,15,0xffeff47d) d=II(b,c,d,a,M1,21,0x85845dd1) a=II(a,b,c,d,M8,6,0x6fa87e4f) b=II(d,a,b,c,M15,10,0xfe2ce6e0) c=II(c,d,a,b,M6,15,0xa3014314) d=II(b,c,d,a,M13,21,0x4e0811a1) a=II(a,b,c,d,M4,6,0xf7537e82) b=II(d,a,b,c,M11,10,0xbd3af235) c=II(c,d,a,b,M2,15,0x2ad7d2bb) d=II(b,c,d,a,M9,21,0xeb86d391)
每轮循环后,将A,B,C,D分别加上a,b,c,d,然后进入下一循环
主循环有四轮,每轮循环都很相似。第一轮进行16次操作。每次操作对 a、b、c和 d中的其中三个作一次非线性函数运算 ,然后将所得结果加上第四个变量,一个子分组和一个常数。再将所得结果向右环移一个不定的数,并加上 a、b、c或 d中之一,最后用该结果取代 a、b、c或 d中之一。
3、结果
当全部信息处理完成后 ,将分组处理的结果进行处理,输出计算结果。
所有这些完成之后 ,将 A、B、C、D分别加上 a、b、c、d。然后用下一分组数据继续运行算法 ,最后的输出是 A、B、C和 D的级联。当全部分组处理完成后,将结果级联 ,即得到了 MD5处理的结果。
注意:
MD5使用4个32位的数据,和数据中的每个32位的数据进行计算,最终输出这4个32位数
2.4、SHA
安全哈希算法(Secure Hash Algorithm)主要适用于数字签名标准(Digital Signature Standard DSS)里面定义的数字签名算法(Digital Signature Algorithm DSA)。对于长度小于2^64位的消息,SHA1会产生一个160位的消息摘要。该算法经过加密专家多年来的发展和改进已日益完善,并被广泛使用。该算法的思想是接收一段明文,然后以一种不可逆的方式将它转换成一段(通常更小)密文,也可以简单的理解为取一串输入码(称为预映射或信息),并把它们转化为长度较短、位数固定的输出序列即散列值(也称为信息摘要或信息认证代码)的过程。散列函数值可以说是对明文的一种“指纹”或是“摘要”所以对散列值的数字签名就可以视为对此明文的数字签名。
SHA256是SHA-2下细分出的一种算法,SHA-2下又可再分为六个不同的算法标准,包括了:SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。
这些变体除了生成摘要的长度 、循环运行的次数等一些微小差异外,算法的基本结构是一致的。
| 算法 | 摘要长度 | 实现方 | |
| SHA-1 | 160 | jdk/bc | |
| SHA-224 | 224 | jdk/bc | |
| SHA-256 | 256 | jdk/bc | |
| SHA-384 | 384 | jdk/bc | |
| SHA-512 | 512 | jdk/bc |
2.4.2、原理【以sha256为例】
常量的初始化、信息预处理、使用到的逻辑运算
1、常量初始化
SHA256算法中用到了8个哈希初值以及64个哈希常量
h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19
这些初值是对自然数中前8个质数(2,3,5,7,11,13,17,19)的平方根的小数部分取前32bit而来
举个例子来说,$ \sqrt{2} $小数部分约为0.414213562373095048,而
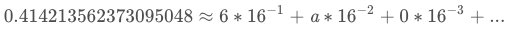
于是,质数2的平方根的小数部分取前32bit就对应出了0x6a09e667
在SHA256算法中,用到的64个常量如下:

428a2f98 71374491 b5c0fbcf e9b5dba5 3956c25b 59f111f1 923f82a4 ab1c5ed5 d807aa98 12835b01 243185be 550c7dc3 72be5d74 80deb1fe 9bdc06a7 c19bf174 e49b69c1 efbe4786 0fc19dc6 240ca1cc 2de92c6f 4a7484aa 5cb0a9dc 76f988da 983e5152 a831c66d b00327c8 bf597fc7 c6e00bf3 d5a79147 06ca6351 14292967 27b70a85 2e1b2138 4d2c6dfc 53380d13 650a7354 766a0abb 81c2c92e 92722c85 a2bfe8a1 a81a664b c24b8b70 c76c51a3 d192e819 d6990624 f40e3585 106aa070 19a4c116 1e376c08 2748774c 34b0bcb5 391c0cb3 4ed8aa4a 5b9cca4f 682e6ff3 748f82ee 78a5636f 84c87814 8cc70208 90befffa a4506ceb bef9a3f7 c67178f2
和8个哈希初值类似,这些常量是对自然数中前64个质数(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97…)的立方根的小数部分取前32bit而来。
2、信息预处理(pre-processing)
SHA256算法中的预处理就是在想要Hash的消息后面补充需要的信息,使整个消息满足指定的结构。信息的预处理分为两个步骤:附加填充比特和附加长度。
STEP1:附加填充比特
在报文末尾进行填充,使报文长度在对512取模以后的余数是448
填充是这样进行的:先补第一个比特为1,然后都补0,直到长度满足对512取模后余数是448。
需要注意的是,信息必须进行填充,也就是说,即使长度已经满足对512取模后余数是448,补位也必须要进行,这时要填充512个比特。
因此,填充是至少补一位,最多补512位。
例:以信息“abc”为例显示补位的过程。
a,b,c对应的ASCII码分别是97,98,99
于是原始信息的二进制编码为:01100001 01100010 01100011
补位第一步,首先补一个“1” : 01100001 01100010 01100011 1
补位第二步,补423个“0”: 01100001 01100010 01100011 10000000 00000000 … 00000000
补位完成后的数据如下(为了简介用16进制表示):
61626380 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
为什么是448?【可以参看MD5也是448位】
因为在第一步的预处理后,第二步会再附加上一个64bit的数据,用来表示原始报文的长度信息。而448+64=512,正好拼成了一个完整的结构。
STEP2:附加长度值
附加长度值就是将原始数据(第一步填充前的消息)的长度信息补到已经进行了填充操作的消息后面。
wiki百科中给出的原文是:append length of message (before pre-processing), in bits, as 64-bit big-endian integer
SHA256用一个64位的数据来表示原始消息的长度。
因此,通过SHA256计算的消息长度必须要小于$ 2^64 $,当然绝大多数情况这足够大了。
长度信息的编码方式为64-bit big-endian integer
关于Big endian的含义,文末给出了补充
回到刚刚的例子,消息“abc”,3个字符,占用24个bit
因此,在进行了补长度的操作以后,整个消息就变成下面这样了(16进制格式)
61626380 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000018
3、逻辑运算
SHA256散列函数中涉及的操作全部是逻辑的位运算:

符号含义:
| 逻辑运算 | 含义 |
|---|---|
| ∧∧ \land ∧ | 按位“与” |
| ¬¬ \neg ¬ | 按位“补” |
| ⊕⊕ \oplus ⊕ | 按位“异或” |
| SnSn S^{n} Sn | 循环右移n个bit |
| RnRn R^{n} Rn | 右移n个bit |
4、计算消息摘要
SHA256算法的主体部分,即消息摘要是如何计算的。
首先:将消息分解成512-bit大小的块(break message into 512-bit chunks)
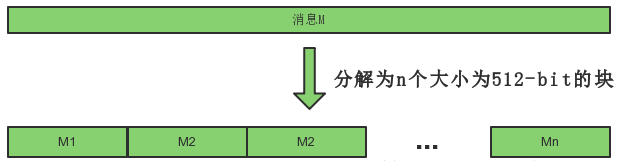
假设消息M可以被分解为n个块,于是整个算法需要做的就是完成n次迭代,n次迭代的结果就是最终的哈希值,即256bit的数字摘要。
一个256-bit的摘要的初始值H0,经过第一个数据块进行运算,得到H1,即完成了第一次迭代
H1经过第二个数据块得到H2,……,依次处理,最后得到Hn,Hn即为最终的256-bit消息摘要
将每次迭代进行的映射用$ Map(H_{i-1}) = H_{i} $表示,于是迭代可以更形象的展示为:
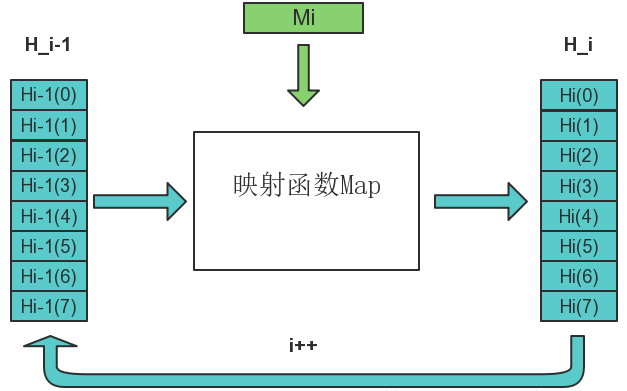
图中256-bit的Hi被描述8个小块,这是因为SHA256算法中的最小运算单元称为“字”(Word),一个字是32位。
此外,第一次迭代中,映射的初值设置为前面介绍的8个哈希初值,如下图所示:
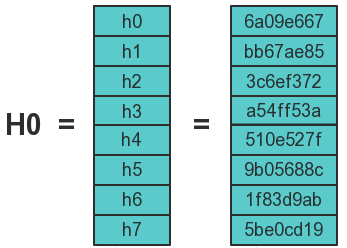
每一次迭代的内容,即映射$ Map(H_{i-1}) = H_{i} $的具体算法
STEP1:构造64个字(word)break chunk into sixteen 32-bit big-endian words w[0], …, w[15]
对于每一块,将块分解为16个32-bit的big-endian的字,记为w[0], …, w[15]
也就是说,前16个字直接由消息的第i个块分解得到
其余的字由如下迭代公式得到:
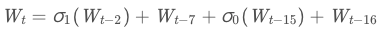
STEP2:进行64次循环
映射 $ Map(H_{i-1}) = H_{i} $ 包含了64次加密循环
即进行64次加密循环即可完成一次迭代
每次加密循环可以由下图描述:
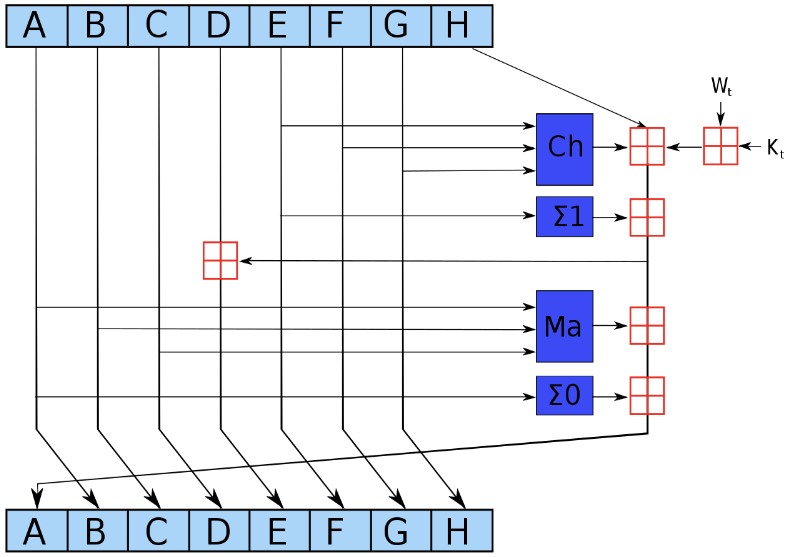
图中,ABCDEFGH这8个字(word)在按照一定的规则进行更新,其中
深蓝色方块是事先定义好的非线性逻辑函数,上文已经做过铺垫
红色田字方块代表 mod $ 2^{32} $ addition,即将两个数字加在一起,如果结果大于$ 2^{32} ,你必须除以,你必须除以,你必须除以 2^{32} $并找到余数。
ABCDEFGH一开始的初始值分别为$ H_{i-1}(0),H_{i-1}(1),…,H_{i-1}(7) $
Kt是第t个密钥,对应我们上文提到的64个常量
Wt是本区块产生第t个word。原消息被切成固定长度512-bit的区块,对每一个区块,产生64个word,通过重复运行循环n次对ABCDEFGH这八个字循环加密。
最后一次循环所产生的八个字合起来即是第i个块对应到的散列字符串$ H_{i} $
伪代码

Note: All variables are unsigned 32 bits and wrap modulo 232 when calculating Initialize variables (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Initialize table of round constants (first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311): k[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Pre-processing: append the bit '1' to the message append k bits '0', where k is the minimum number >= 0 such that the resulting message length (in bits) is congruent to 448(mod 512) append length of message (before pre-processing), in bits, as 64-bit big-endian integer Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk break chunk into sixteen 32-bit big-endian words w[0..15] Extend the sixteen 32-bit words into sixty-four 32-bit words: for i from 16 to 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor(w[i-15] rightshift 3) s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor(w[i-2] rightshift 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Initialize hash value for this chunk: a := h0 b := h1 c := h2 d := h3 e := h4 f := h5 g := h6 h := h7 Main loop: for i from 0 to 63 s0 := (a rightrotate 2) xor (a rightrotate 13) xor(a rightrotate 22) maj := (a and b) xor (a and c) xor(b and c) t2 := s0 + maj s1 := (e rightrotate 6) xor (e rightrotate 11) xor(e rightrotate 25) ch := (e and f) xor ((not e) and g) t1 := h + s1 + ch + k[i] + w[i] h := g g := f f := e e := d + t1 d := c c := b b := a a := t1 + t2 Add this chunk's hash to result so far: h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Produce the final hash value (big-endian): digest = hash = h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
参看地址:https://blog.csdn.net/u011583927/article/details/80905740
2.5、HMAC【盐+hash算法】
在哈希算法时,如果存储用户的哈希口令时,推荐要加盐存储,目的就在于抵御彩虹表攻击。如,
digest = hash(input) //加盐 digest = hash(salt + input)
salt可以看作是一个额外的“认证码”,同样的输入,不同的认证码,会产生不同的输出。因此,要验证输出的哈希,必须同时提供“认证码”。
Hmac算法就是一种基于密钥的消息认证码算法,它的全称是Hash-based Message Authentication Code,是一种更安全的消息摘要算法。
Hmac算法总是和某种哈希算法配合起来用的。例如,我们使用MD5算法,对应的就是HmacMD5算法,它相当于“加盐”的MD5:
HmacMD5 ≈ md5(secure_random_key, input)
因此,HmacMD5可以看作带有一个安全的key的MD5。使用HmacMD5而不是用MD5加salt,有如下好处:
- HmacMD5使用的key长度是64字节,更安全;
- Hmac是标准算法,同样适用于SHA-1等其他哈希算法;
- Hmac输出和原有的哈希算法长度一致。
可见,Hmac本质上就是把key混入摘要的算法。验证此哈希时,除了原始的输入数据,还要提供key。
HMAC是密钥相关的哈希运算消息认证码,HMAC运算利用哈希算法,以一个密钥和一个消息为输入,生成一个消息摘要作为输出。
运算作用
| 算法 | 摘要长度 | 实现方 | |
| HmacMD2 | 128 | bc | |
| HmacMD4 | 128 | bc | |
| HmacMD5 | 128 | jdk/bc | |
| HmacSHA1 | 160 | jdk/bc | |
| HmacSHA224 | 224 | jdk/bc | |
| HmacSHA256 | 256 | jdk/bc | |
| HmacSHA384 | 384 | jdk/bc | |
| HmacSHA512 | 512 | jdk/bc | |
| HmacRipeMD128 | 128 | bc | |
| HmacRipeMD160 | 160 | bc |
BC加密包:The Bouncy Castle Crypto package is a Java implementation of cryptographic algorithms. This jar contains JCE provider and lightweight API for the Bouncy Castle Cryptography APIs for JDK 1.5 to JDK 1.8.
为了保证安全,一般不会自己指定key,而是通过Java标准库的KeyGenerator生成一个安全的随机的key。下面是使用HmacMD5的代码:
public static void main(String[] args) throws Exception { KeyGenerator keyGen = KeyGenerator.getInstance("HmacMD5"); SecretKey key = keyGen.generateKey(); // 打印随机生成的key: byte[] skey = key.getEncoded(); System.out.println(new BigInteger(1, skey).toString(16)); Mac mac = Mac.getInstance("HmacMD5"); mac.init(key); mac.update("HelloWorld".getBytes("UTF-8")); byte[] result = mac.doFinal(); System.out.println(new BigInteger(1, result).toString(16)); }
使用HmacMD5的步骤是:
- 通过名称
HmacMD5获取KeyGenerator实例; - 通过
KeyGenerator创建一个SecretKey实例; - 通过名称
HmacMD5获取Mac实例; - 用
SecretKey初始化Mac实例; - 对
Mac实例反复调用update(byte[])输入数据; - 调用
Mac实例的doFinal()获取最终的哈希值。
我们可以用Hmac算法取代原有的自定义的加盐算法,因此,存储用户名和口令的数据库结构如下:
| username | secret_key (64 bytes) | password |
|---|---|---|
| bob | a8c06e05f92e...5e16 | 7e0387872a57c85ef6dddbaa12f376de |
| alice | e6a343693985...f4be | c1f929ac2552642b302e739bc0cdbaac |
| tim | f27a973dfdc0...6003 | af57651c3a8a73303515804d4af43790 |
验证计算
有了Hmac计算的哈希和SecretKey,我们想要验证怎么办?这时,SecretKey不能从KeyGenerator生成,而是从一个byte[]数组恢复:

public class Main { public static void main(String[] args) throws Exception { byte[] hkey = new byte[] { 106, 70, -110, 125, 39, -20, 52, 56, 85, 9, -19, -72, 52, -53, 52, -45, -6, 119, -63, 30, 20, -83, -28, 77, 98, 109, -32, -76, 121, -106, 0, -74, -107, -114, -45, 104, -104, -8, 2, 121, 6, 97, -18, -13, -63, -30, -125, -103, -80, -46, 113, -14, 68, 32, -46, 101, -116, -104, -81, -108, 122, 89, -106, -109 }; SecretKey key = new SecretKeySpec(hkey, "HmacMD5"); Mac mac = Mac.getInstance("HmacMD5"); mac.init(key); mac.update("HelloWorld".getBytes("UTF-8")); byte[] result = mac.doFinal(); System.out.println(Arrays.toString(result)); // [126, 59, 37, 63, 73, 90, 111, -96, -77, 15, 82, -74, 122, -55, -67, 54] } }
2.6、RIPEMD算法
原始完整性校验消息摘要
RIPEMD(RACE Integrity Primitives Evaluation Message Digest,RACE原始完整性校验消息摘要),是Hans Dobbertin等3人在md4,md5的基础上,于1996年提出来的。算法共有4个标准128、160、256和320,其对应输出长度分别为16字节、20字节、32字节和40字节。不过,让人难以致信的是RIPEMD的设计者们根本就没有真正设计256和320位这2种标准,他们只是在128位和160位的基础上,修改了初始参数和s-box来达到输出为256和320位的目的。所以,256位的强度和128相当,而320位的强度和160位相当。RIPEMD建立在md的基础之上,所以,其添加数据的方式和md5完全一样。
| 算法 | 摘要长度 | 备注 |
| RipeMD128 | 128 | BouncyCastle实现 |
| RipeMD160 | 160 | BouncyCastle实现 |
| RipeMD256 | 256 | BouncyCastle实现 |
| RipeMD320 | 320 | BouncyCastle实现 |
也支持hmac方式使用,HmacRipeMD消息摘要的长度与相应的摘要算法的摘要长度相同:HmacRipeMD128与RipeMD128相对应,消息摘要长度都是32个字符的16进制串。HmacRipeMD160与RipeMD160相对应,消息摘要长度都是40个字符的16进制串。
2.7、其他算法
BouncyCastle不仅仅提供了HmacRipeMD算法的实现,还提供了HmacTiger算法的实现。实现方式与上边的代码清单相似
除了MD、SHA和MAC三大主流信息摘要算法之外,还有一些不常见的消息摘要算法。包括RipeMD系列、Tiger、Whirlpool和Gost3411算法。同时,RipeMD算法和MAC算法系列相结合,有产生了HmacRipeMD128和HmacRipeMD160两种算法。
针对这些算法进行简单介绍
1、RipeMD算法:针对MD4和MD5算法缺陷分析提出的算法。这些算法主要是针对摘要值得长度进行了区分
2、Tiger算法:号称最快的Hash算法,专门针对64为机器做优化了。其消息长度为192位
3、Whirlpool:被列入iso标准。与AES加密标准使用了相同的转化技术,极大提高了安全性,被称为最安全的摘要算法,长度为512位
4、Gost3411:信息摘要长度为256位
这些算法的实现java6都没提供。这里BouncyCastle进行了支持。其实这些算法的调用都一个样,就是换一个调用的名字而已。
详见代码库:algorithm-sign/algorithm-sign-impl/src/main/java/com/github/bjlhx15/security/base006others 实现
http://www.bouncycastle.org/java.html
http://mvnrepository.com/artifact/org.bouncycastle/bcprov-jdk15on
三、nodejs版本
nodejs 提供的基本模块crypto,涵盖了大部分的算法实现。
rypto 模块提供了加密功能,包括一组用于包装 OpenSSL 的哈希,HMAC,加密,解密,签名和验证函数。
使用 require('crypto') 来访问这个模块。
参看地址:https://www.bookstack.cn/read/nodejs-api-doc-cn/crypto-README.md
3.1、编码算法
Buffers 通常用于代表编码的字符序列,比如 UTF8 、 UCS2 、 Base64 甚至 Hex-encoded 的数据。有可能通过使用一个明确的编码方法在 Buffers 和普通的 JavaScript 字符串对象之间进行相互转换。
示例:
const buf = Buffer.from('hello world', 'ascii');
console.log(buf.toString('hex'));
// prints: 68656c6c6f20776f726c64
console.log(buf.toString('base64'));
// prints: aGVsbG8gd29ybGQ=
Node.js 目前支持的字符编码包括:
-
'ascii'- 仅支持 7位 ASCII 数据。如果设置去掉高位的话,这种编码方法是非常快的。 -
'utf8'- 多字节编码的Unicode字符。许多网页和其他文档格式使用 UTF-8 。 -
'utf16le'- 2或4个字节,小端编码的Unicode字符。支持代理对(U+10000 to U+10FFFF)。 -
'ucs2'-'utf16le'的别名。 -
'base64'- Base64 字符串编码。当从一个字符串创建一个 buffer 时,按照 RFC 4648, Section 5 里的规定,这种编码也将接受正确的“URL和文件名安全字母”。 -
'binary'- 一种把 buffer 编码成一字节(latin-1)编码字符串的方式。目前不支持'latin-1'字符串。通过'binary'来代替'latin-1'使用'latin-1'编码。 -
'hex'- 将每个字节编码为两个十六进制字符。
更多示例参看:https://github.com/bjlhx15/algorithm-sign-nodejs.git
3.2、散列算法
- hash.update(data[, input_encoding])
- hash.digest([encoding])
示例:
function mdAndSha(algorithmName, srcData) { const crypto = require('crypto'); const hash = crypto.createHash(algorithmName); // 可任意多次调用update(): hash.update(srcData); // hash.update('Hello, nodejs!'); const value=hash.digest('hex') console.log(value); return value; } var baseAlgorithmName= { md5 : "md5", sha1 : "sha1", sha224 : "sha224", sha256 : "sha256", sha384 : "sha384", sha512 : "sha512" } module.exports = { mdAndSha,baseAlgorithmName }
测试
function main(){ var base001mdAndSha=require("../main/base001hash") base001mdAndSha.mdAndSha(base001mdAndSha.baseAlgorithmName.md5,"hello world"); base001mdAndSha.mdAndSha(base001mdAndSha.baseAlgorithmName.sha1,"hello world"); base001mdAndSha.mdAndSha(base001mdAndSha.baseAlgorithmName.sha224,"hello world"); base001mdAndSha.mdAndSha(base001mdAndSha.baseAlgorithmName.sha256,"hello world"); base001mdAndSha.mdAndSha(base001mdAndSha.baseAlgorithmName.sha384,"hello world"); base001mdAndSha.mdAndSha(base001mdAndSha.baseAlgorithmName.sha512,"hello world"); } main();
更多参看:https://github.com/bjlhx15/algorithm-sign-nodejs.git
更多:https://www.bookstack.cn/read/nodejs-api-doc-cn/crypto-class_Hash.md
3.3、hmac
更多参看:https://github.com/bjlhx15/algorithm-sign-nodejs.git
更多:https://www.bookstack.cn/read/nodejs-api-doc-cn/crypto-class_Hmac.md



