005-排序算法-归并排序

一、概述

　　基本思想：采用分治法，将已有的有序子序列合并，得到一个完整的有序序列

排序方法	时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定

分治算法

　　分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。

　　分治算法的一般步骤：

　　（1）分解，将要解决的问题划分成若干规模较小的同类问题；

　　（2）求解，当子问题划分得足够小时，用较简单的方法解决；

　　（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

1.1、算法说明

　　

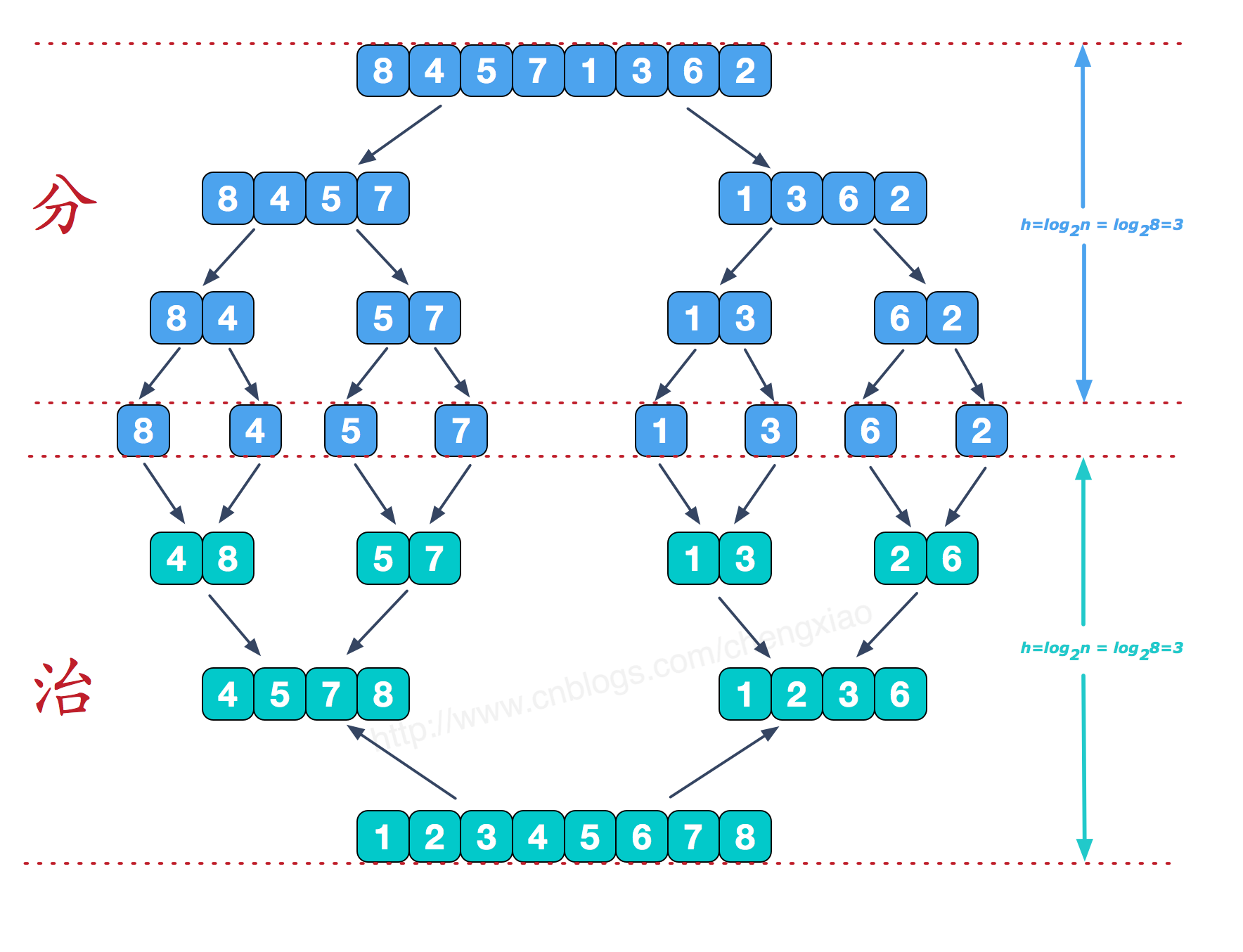
　　下图更加能够说明分治法

　　　　

1.2、算法实现

　　将长度为 n 的序列分成两个长度为 2/n 的子序列，然后对着两个子序列进行归并排序，子序列又被分成子序列再进行归并排序，最终对有序子序列进行归并，得到最终的有序序列。 

　　根据具体的实现，归并排序包括"从上往下"和"从下往上"2种方式。

    public static int[] mergeSort(int[] nums, int l, int h) {
        if (l == h)
            return new int[] { nums[l] };

        int mid = l + (h - l) / 2;//从中间拆分
        int[] leftArr = mergeSort(nums, l, mid); //左有序数组 拆分
        int[] rightArr = mergeSort(nums, mid + 1, h); //右有序数组 拆分
        int[] newNum = new int[leftArr.length + rightArr.length]; //新有序数组

        int m = 0, i = 0, j = 0;
        while (i < leftArr.length && j < rightArr.length) {
            newNum[m++] = leftArr[i] < rightArr[j] ? leftArr[i++] : rightArr[j++];
        }
        while (i < leftArr.length)
            newNum[m++] = leftArr[i++];
        while (j < rightArr.length)
            newNum[m++] = rightArr[j++];
        return newNum;
    }

 

 

代码地址：地址 中的algorithm-001-sort中 MergeSort