002-排序算法-快速排序

一、概述

　　快速排序(Quick Sort)使用分治法策略。

　　快速排序的基本思想：通过一趟排序以基准元素[一般选择序列的第一个元素]为界限将待排序列分割成两个独立的部分，然后再对两个独立的部分进行快排，依次类推直到序列整体有序。

排序方法	时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
快速排序	O(nlogn)	O(n^2)	O(nlogn)	O(logn)	不稳定

稳定性

　　快速排序算法的稳定性取决于和基准值交换的那个数的大小，如果它们相等的话，那么稳定性就被破坏了，所以快速排序是一种不稳定的排序方法。

时间复杂度

　　最坏的情况就是每次划分之后，一边只有一个元素，另一边有n-1个元素，这样就得划n-1次，这时候时间复杂度为O(n²)；

　　快速排序的快慢取决于区域划分的次数，理想情况下是每次都等分，所以划分次数为logn（即log₂n)，时间复杂度为T[n] = 2T[n/2] + O(n)其中O(n)为PARTITION()的时间复杂度，对比主定理，T[n]= aT[n/b]+f (n)，我们的快速排序中：a = 2, b = 2, f(n) = O(n)

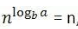
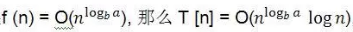　　如果,既时间复杂度：O(nlogn)

 1.1、算法说明

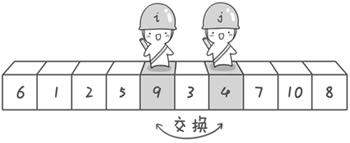
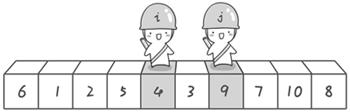
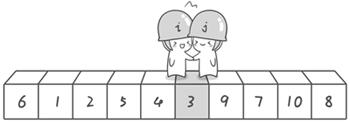
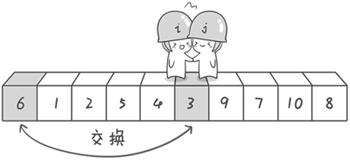
　　排序：6 1 2 7 9 3 4 5 10 8

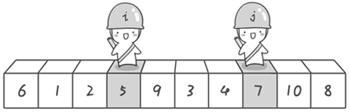
　　过程：以第一个数6为基准值，从右侧开始，找到一个比6小的a[j]，然后从左侧开始找一个比6大的a[j],进行交换，一直循环即可，直到 i 和 j 相遇a[i]=a[j]；

　　　　

　　　　　　 → 

　　　　　　→

　　　　→→

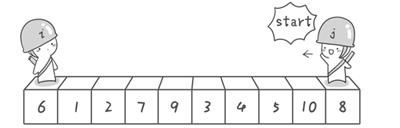
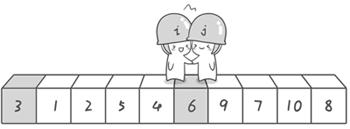
　　后续的话，分为两部分递归调用上述过程即可

1.2、算法实现

    public static void quickSort2(int a[], int low, int high) {
        if (low < high) {
            int i = low, j = high, key = a[i];
            while (i < j) {
                //先看右边，依次往左递减 找到比基准值 key 小的 退出循环，准备和下面的大于的换
                while (i < j && key <= a[j]) {
                    j--;
                }
                //在看做边，依次往右递增 找到比基准值key 大的的 退出循环，准备和上面面的小于的换
                while (i < j && a[i] <= key) {
                    i++;
                }
                //如果i<j，交换它们
                if (i < j) {
                    int tmp = a[j];
                    a[j] = a[i];
                    a[i] = tmp;
                }
            }
            //最后将基准为与i和j相等位置的数字交换
            a[low] = a[i];
            a[i] = key;//把基准值放到合适的位置
            //递归调用左半数组
            quickSort2(a, low, j - 1);
            //递归调用右半数组
            quickSort2(a, j + 1, high);
        }
    }

 

代码地址：地址 中的rithm-001-sort中 QuickSort 

参看地址：https://blog.csdn.net/shujuelin/article/details/82423852

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

大树