北大poj-1021

2D-Nim

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4066		Accepted: 1851

Description

The 2D-Nim board game is played on a grid, with pieces on the grid points. On each move, a player may remove any positive number of contiguous pieces in any row or column. The player who removes the last piece wins. For example, consider the left grid in the following figure.

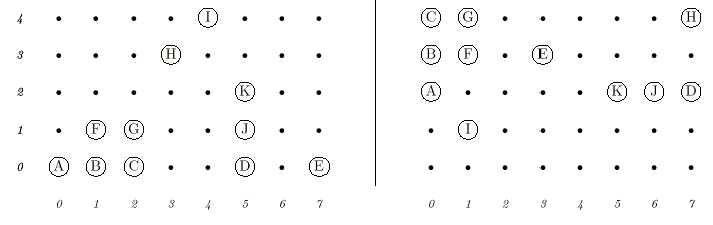
The player on move may remove (A), (B), (A, B), (A, B, C), or (B,F), etc., but may not remove (A, C), (D, E), (H, I) or (B, G).
For purposes of writing 2D-Nim-playing software, a certain programmer wants to be able to tell whether or not a certain position has ever been analyzed previously. Because of the rules of 2D-Nim, it should be clear that the two boards above are essentially equivalent. That is, if there is a winning strategy for the left board, the same one must apply to the right board. The fact that the contiguous groups of pieces appear in different places and orientations is clearly irrelevant. All that matters is that the same clusters of pieces (a cluster being a set of contiguous pieces that can be reached from each other by a sequence of one-square vertical or horizontal moves) appear in each. For example, the cluster of pieces (A, B, C, F, G) appears on both boards, but it has been reflected (swapping left and right), rotated, and moved. Your task is to determine whether two given board states are equivalent in this sense or not.

Input

The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by the input data for each test case. The first line of each test case consists of three integers W, H, and n (1 ≤ W, H ≤ 100). W is the width, and H is the height of the grid in terms of the number of grid points. n is the number of pieces on each board. The second line of each test case contains a sequence of n pairs of integers xi , yi, giving the coordinates of the pieces on the first board (0 ≤ xi < W and 0 ≤ yi < H). The third line of the test case describes the coordinates of the pieces on the second board in the same format.

Output

Your program should produce a single line for each test case containing a word YES or NO indicating whether the two boards are equivalent or not.

Sample Input

2
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 5 2 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 6 1 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4

Sample Output

YES
NO

Source

Tehran 2002, First Iran Nationwide Internet Programming Contest

 

分析：

需要依据题目，提取图像特征，特征一致则为YES，特征不一致则为NO。

解题：

提取了2个特征：

1）每一个点的邻接关系：统计四个方向上邻接点数量分布，即有0、1、2、3、4个点相邻的数量。

2）点的连通量：在纵向和横向两个方向上，统计连线点的分布，即有1、2、...、99、100个点连成一线的数量。

 

PS：这两个条件为必要不充分条件。discus中有用例我没跑过，但是poj AC了，poj的数据弱了。至于充分条件，目前我还没想出如何证明。

 

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct
{
    int width;
    int height;
    int num;
    int map[2][100][100];
}Picture;

typedef struct
{
    int x;
    int y;
    int factor;
}Piont;

Picture pic;
Piont points[2][10000];
int factorCnt[2][5];
int connectCnt[2][101];
int connectMax[2];

void Input()
{
    int i, j, x, y = 0;
    memset(&pic, 0, sizeof(pic));
    scanf("%d %d %d", &pic.width, &pic.height, &pic.num);

    for(j = 0; j < 2; j++)
    {
        for(i = 0; i < pic.num; i++)
        {
            scanf("%d %d", &x, &y);
            pic.map[j][y][x] = 1;
            points[j][i].x = x;
            points[j][i].y = y;
        }
    }
/*
    for(j = 0; j < 2; j++)
    {
        for(y = pic.height-1; y >= 0; y--)
        {
            for(x = 0; x < pic.width; x++)
            {
                printf("%d ", pic.map[j][y][x]);
            }
            printf("\n");
        }
        printf("------------------------\n");
    }
*/
}

void CalcFactor()
{
    int i, j, x, y, factor;
    memset(factorCnt, 0, sizeof(factorCnt));
    for(j = 0; j < 2; j++)
    {
        for(i = 0; i < pic.num; i++)
        {
            x = points[j][i].x;
            y = points[j][i].y;
            factor = (x > 0) ? pic.map[j][y][x-1] : 0;
            factor += (x < pic.width-1) ? pic.map[j][y][x+1] : 0;
            factor += (y > 0) ? pic.map[j][y-1][x] : 0;
            factor += (y < pic.height-1) ? pic.map[j][y+1][x] : 0;
            points[j][i].factor = factor;
            factorCnt[j][factor]++;
        }
    }
/*
    for(j = 0; j < 2; j++)
    {
        for(i = 0; i < pic.num; i++)
        {
            printf("%d   ", points[j][i].factor);
        }
        printf("\n");
    }
    printf("------------------------\n");
*/
}

void CheckResult()
{
    int i, j = 0;
    for(i = 0; i < 5; i++)
    {
        if(factorCnt[0][i] != factorCnt[1][i]) break;
    }

    if(connectMax[0] != connectMax[1])
    {
        printf("NO\n");
        return;
    }

    for(j = 0; j < connectMax[0]; j++)
    {
        if(connectCnt[0][j] != connectCnt[1][j]) break;
    }

    if(i != 5 || j != connectMax[0])
    {
        printf("NO\n");
    }
    else
    {
        printf("YES\n");
    }
}

void CalcConnect()
{
    int j, x, y, connect;
    memset(connectMax, 0, sizeof(connectMax));
    memset(connectCnt, 0, sizeof(connectCnt));
    for(j = 0; j < 2; j++)
    {
        for(y = 0; y < pic.height; y++)
        {
            for(x = 0; x < pic.width; x++)
            {
                if(pic.map[j][y][x] != 1) continue;
                connect = 1;
                while(++x < pic.width && pic.map[j][y][x] == 1)
                {
                    connect++;
                }
                connectCnt[j][connect]++;
                if(connect > connectMax[j]) connectMax[j] = connect;
            }
        }

        for(x = 0; x < pic.width; x++)
        {
            for(y = 0; y < pic.height; y++)
            {
                if(pic.map[j][y][x] != 1) continue;
                connect = 1;
                while(++y < pic.height && pic.map[j][y][x] == 1)
                {
                    connect++;
                }
                connectCnt[j][connect]++;
                if(connect > connectMax[j]) connectMax[j] = connect;
            }
        }
    }
}

void Proc()
{
    CalcFactor();
    CalcConnect();
    CheckResult();
}

int main()
{
    int num = 0;
    scanf("%d", &num);
    while(num--)
    {
        Input();
        Proc();
    }
    return 0;
}