CPA教材财管2024-第六章期权价值评估

第六章期权价值评估

第一节衍生工具概述

衍生工具是从原生工具中派生的一种合同，其价值随原生工具价格的波动而波动该原生工具也叫基础资产或标的资产，可以是金融资产或实物资产。

一、衍生工具种类

点击查看代码

常见的衍生工具包括远期合约、期货合约、互换合约、期权合约等，

(一)远期合约

远期合约(forwardcontract)是一种最简单的衍生工具，是合约双方同意在未来日期按照事先约定的价格交换资产的合约，该合约会指明买卖的商品或金融工具的种类、价格及交割结算的日期。远期合约的条款是为买卖双方量身定制的，因合约双方的需要不同而不同。远期合约通常不在交易所内交易，而是场外交易(0TC)。如同即期交易样，远期合约对交易双方都有约束，是必须履行的协议。

(二)期货合约

期货合约(futurescontract)是指在约定的将来某个日期按约定的条件(包括价格交割地点、交割方式)买人或卖出一定标准数量、质量某种资产的合约。期货合约是由期货交易所统一制定的标准化合约，是买卖双方同意在约定时间按约定价格接收、交付一定标准数量、质量的某种资产的协议。期货交易通常集中在期货交易所进行，但亦有部分期货合约可通过柜台交易进行。与远期合约一样，期货合约对交易双方都有约束是必须履行的协议。

(三)互换合约

互换合约(swapcontract)，是指交易双方约定在未来某一期限相互交换各自持有的资产或现金流的交易形式。互换能满足交易者对非标准化交易的需求，运用面广，期限灵活，长短随意。互换的种类通常包括÷利率互换、货币互换、商品互换、股权互换信用互换、气候互换(碳互换)和期权互换等。其中，利率互换是指双方同意在未来的一定期限内根据同种货币的同样名义本金交换现金流，其中一方的现金流量根据浮动利率计算，而另一方的现金流量根据固定利率计算。货币互换是指将一种货币的本金和固定利息与另一货币的等价本金和固定利息进行交换。商品互换是指交易双方为了管理商品价格风险，同意交换与商品价格有关的现金流，包括固定价格及浮动价格的商品价格互换和商品价格与利率的互换。

(四)期权合约

期权合约(optioncontract)是在期货合约的基础上产生的一种衍生工具，它是在某一特定日期或该日期之前的任何时间以固定价格购买或者出售某种资产(包括股票、债券、货币、股票指数、商品期货等)的权利。与其他衍生工具不同，期权从其本质上讲，是将权利和义务分开进行定价，使得权利的受让人(即期权的买方)可在规定时间内对于是否进行交易行使其权利，而义务方(即期权的卖方)必须行义务。期权的买方只有权利而无义务，风险是有限的(最大亏损值为权利金)，而获利在理论上是无限的；期权的卖方则只有义务而无权利，收益是有限的(最大收益值为权利金)，而风险在理论上是无限的。此外，期权的买方无须付出保证金，卖方则必须支付保证金以作为履行义务的财务担保。

二、衍生工具交易特点

点击查看代码

与基础资产相比，衍生工具在交易方面具有很多特点。
第一，未来性。衍生工具是在现时对基础资产未来可能产生的结果进行交易，交易结果要在未来时刻才能确定。这就要求交易双方对利率、汇率、股价等各类基础资产价格的未来变动趋势作出判断，而判断准确与否直接决定了交易者的盈亏。第二，灵活性。衍生工具的种类繁多，其设计和创造具有较高的灵活性，与基础资产相比更能适应各类市场参与者的需要。第三，杠杆性。衍生工具可以使交易者用较少成本获取现货市场上用较多资金才能完成的结果，因此具有高杠杆性。第四，风险性。衍生工具是在市场动荡不安的环境下，为实现交易保值和风险防范而进行的工具创新，但其内在的杠杆作用和交易复杂性也决定了衍生工具交易的高风险性。如果利用衍生工具交易进行投机，则有可能造成巨大损失。第五，虚拟性。衍生工具的交易对象是对基础资产在未来特定条件下进行处置的权利和义务。衍生工具本身没有价值，它只是一种收益获取权的凭证，其交易独立于现实资本运动之外，具有虚拟性。

三、衍生工具交易目的

点击查看代码

衍生工具可用于多种用途，包括套期保值、投机获利等。套期保值是指为冲抵风险而买卖相应的衍生工具的行为，与套期保值相反的便是投机行为。套期保值的目的是降低风险，投机的目的是承担额外的风险以盈利；套期保值的结果是降低了风险，投机的结果是增加了风险。

下面以期货为例，说明如何利用期货进行套期保值和投机获利。

(一)套期保值

点击查看代码

期货的套期保值亦称为期货对冲，是指为配合现货市场上的交易，而在期货市场上做与现货市场商品相同或相近但交易部位相反的买卖行为，以便将现货市场价格波动的风险在期货市场上抵消。
期货的套期保值交易之所以有利于回避价格风险，其基本原理就在于某一特定商品的期货价格和现货价格受相同的经济因素影响和制约。
利用期货套期保值有两种方式：
第一，空头套期保值÷如果某公司要在未来某时出售某种资产，可以通过持有该资产期货合约的空头来对冲风险。如果到期日资产价格下降，现货出售资产亏损，则期货的空头获利；如果到期日资产价格上升，现货出售资产获利，则期货的空头亏损。第二，多头套期保值÷如果要在未来某时买人某种资产，则可采用持有该资产期货合约的多头来对冲风险。如果到期日资产价格上升，现货购买资产亏损，则期货的多头获利÷如果到期日资产价格下降，现货购买资产获利，则期货的多头亏损。利用期货套期保值一般涉及两个时间的四个交易。表6-1至表6-4分别显示了商品期货、外汇期货两种期货空头套期保值和多头套期保值的例子，从中可以看到期货套期保值是怎样降低风险的。
表6-1
商品期货空头套期保值实例
表6-2
商品期货多头套期保值实例
表6-4
外汇期货多头套期保值实例

(二)投机获利

点击查看代码

期货投机是指基于对市场价格走势的预期，为了盈利在期货市场上进行的买卖行为。由于远期市场价格的波动性，与套期保值相反，期货的投机会增加风险。例如，假设原油市场现价每桶75美元，而公司判断原油市场在半年后会大跌至每桶50美元，因此公司卖出100万桶半年后交割的原油期货，卖出价格为每桶80美元。如果市场变化如公司预期，则公司将盈利3000万美元。但是，半年后，原油价格涨为每100美元，公司因此亏损2000万美元。假设半年后，原油价格涨为每桶200美元，则公司亏损将为1.2亿美元。

第二节期权的概念、类型和投资策略

一、期权的概念

点击查看代码

期权是一种合约，该合约赋予持有人在某一特定日期或该日之前的任何时间以固定价格购进或售出约定数量某种资产的权利。
例如，王先生20x0年以100万元的价格购入一处房产，同时与房地产商A签订了一项期权合约。合约赋予王先生在20x2年8月16日或者此前的任何时间，以120万元的价格将该房产出售给A的权利。如果在到期日之前该房产的市场价格高于120万元则王先生不会执行期权，而选择在市场上出售或者继续持有。如果该房产的市价在到期日之前低于120万元，则王先生可以选择执行期权，将房产出售给A并获得120万元现金。

期权定义的要点如下：

点击查看代码

(一)期权是一种权利

期权合约至少涉及购买人和出售人两方。获得期权的一方称为期权购买人，出售期权的一方称为期权出售人。交易完成后，购买人成为期权持有人。期权赋予持有人做某件事的权利，但他不承担必须履行的义务，可以选择执行或者不执行该权利。持有人仅在执行期权有利时才会利用它，否则该期权将被放弃。在这种意义上说期权是一种“特权”，因为持有人只享有权利而不承担相应的义务。期权合约不同于远期合约和期货合约。在远期和期货合约中，双方的权利和义务是对等的，双方互相承担责任，各自具有要求对方履约的权利。当然，与此相适应，投资者签订远期或期货合约时不需要向对方支付任何费用，而投资者购买期权合约必须支付期权费，作为不承担义务的代价。

(二)期权的标的资产

期权的标的资产是指选择购买或出售的资产。它包括股票、政府债券、货币、股票指数、商品期货、房地产等。期权是这些标的物“衍生”的，因此，称为衍生工具。值得注意的是，期权出售人不一定拥有标的资产。例如出售IBM公司股票期权的人不一定是IBM公司本身，他也未必持有IBM的股票，期权是可以“卖空”的。期权购买人也不一定真的想购买标的资产。因此，期权到期时双方不一定进行标的物的实物交割而只需按价差补足价款即可。一个公司的股票期权在市场上被交易，该期权的源生股票发行公司并不能影响期权市场，该公司并不从期权市场上筹集资金。期权持有人没有选举公司董事、决定公司重大事项的投票权，也不能获得该公司的股利。

(三)到期日

双方约定的期权到期的那一天称为到期日。在那一天之后，期权失效。按照期权执行时间分为欧式期权和美式期权。如果该期权只能在到期日执行，称为欧式期权。如果该期权可以在到期日或到期日之前的任何时间执行，称为美式期权。

(四)期权的执行

依据期权合约购进或售出标的资产的行为称为执行。在期权合约中约定的、期权持有人据以购进或售出标的资产的固定价格，称为执行价格。

二、期权的类型

点击查看代码

按照合约授予期权持有人权利的类别，期权分为看涨期权和看跌期权两大类
首先是看涨期权。看涨期权是指期权赋予持有人在到期日或到期日之前，以固定价格购买标的资产的权利。其授予权利的特征是购买。因此，也可以称为择购期权、买入期权或买权。
例如，一股每股执行价格为80元的ABC公司股票的3个月后到期的看涨期权，允许其持有人在到期日之前的任意一天，包括到期日当天，以80元的价格购人ABC公司的股票。当ABC公司的股票超过80元时，期权持有人有可能会以执行价格购买标的资产。如果标的股票的价格一直低于80元，持有人则不会执行期权。他并不被要求必须执行该期权。期权未被执行，过期后不再具有价值。
看涨期权的执行净收入，被称为看涨期权到期日价值，它等于股票价格减去执行价格的价差。如果在到期日股票价格高于执行价格，看涨期权的到期日价值随标的资产价值上升而上升；如果在到期日股票价格低于执行价格，则看涨期权没有价值。期权到期日价值没有考虑当初购买期权的成本。期权的购买成本称为期权费(或权利金)，是指看涨期权购买人为获得在对自己有利时执行期权的权利所必须支付的补偿费用。期权到期日价值减去期权费后的剩余，称为期权购买人的“损益”。
其次是看跌期权。看跌期权是指期权赋予持有人在到期日或到期日前，以固定价格出售标的资产的权利。其授予权利的特征是出售。因此，也可以称为售期权、卖出期权或卖权。
例如，一股每股执行价格为80元的ABC公司股票的7个月后到期的看跌期权，允许其持有人在到期日之前的任意一天，包括到期日当天，以80元的价格出售ABC公司的股票。当ABC公司的股票低于80元时，看跌期权持有人会要求以执行价格出售标的资产看跌期权的出售方必须接受。如果标的股票的价格一直高于80元，持有人则不会执行期权。他并不被要求必须执行该期权。期权未被执行，过期后不再具有价值。
看跌期权的执行净收入，被称为看跌期权到期日价值，它等于执行价格减去股票价格的价差。如果在到期日股票价格低于执行价格，看跌期权的到期日价值随标的资产价值下降而上升；如果在到期日股票价格高于执行价格，则看跌期权没有价值。看跌期权到期日价值没有考虑当初购买期权的成本。看跌期权的到期日价值减去期权费后的剩余称为期权购买人的“损益”。
为了评估期权的价值，需要先知道期权的到期日价值。期权的到期日价值，是指到期时执行期权可以取得的净收入，它依赖于标的股票的到期日价格和执行价格。执行价格是已知的，而股票到期日的市场价格此前是未知的。但是，期权的到期日价值与股票的市场价格之间存在函数关系。这种函数关系，因期权的类别而异。
对于看涨期权和看跌期权，到期日价值的计算又分为买人和卖出两种。下面我们分别说明这四种情景下期权到期日价值和股价的关系。为简便起见，我们假设各种期权均持有至到期日，不提前执行，并且忽略交易成本。

(一)买入看涨期权

点击查看代码

买入看涨期权形成的金融头寸，被称为“多头看涨头寸”
【例6-1】投资者购买一项ABC公司的股票看涨期权，标的股票的当前市价为100元，执行价格为100元，到期日为1年后的今天，期权价格为5元。买入后，投资者就持有了看涨头寸，期待未来股价上涨以获取净收益。
多头看涨期权的净损益有以下四种可能：
(1)股票市价小于或等于100元，看涨期权买方不会执行期权，没有净收入，即期权到期日价值为0，其净损益为-5元(期权价值0元-期权成本5元)。
(2)股票市价大于100元并小于105元，例如股票市价为103元，投资者会执行期权。以100元购买该公司的1股股票，在市场上将其出售得到103元，净收入为3元(股票市价103元-执行价格100元)，即期权到期日价值为3元，买方期权净损益为-2元(期权价值3元-期权成本5元)。
(3)股票市价等于105元，投资者会执行期权，取得净收入5元(股票市价105元-执行价格100元)，即期权到期日价值为5元。多头看涨期权的净损益为0元(期权价值5元-期权成本5元)。
(4)股票市价大于105元，假设为110元，投资者会执行期权，净收入为10元(股票市价110元-执行价格100元)，即期权的到期日价值为10元。投资者的净损益为5元(期权价值10元-期权成本5元)。
综合上述四种情况，可以概括为以下表达式：
多头看涨期权到期日价值=max(股票市价-执行价格，0)
该式表明÷如果股票市价＞执行价格，会执行期权，看涨期权价值等于“股票市价-执行价格”；如果股票市价＜执行价格，不会执行期权，看涨期权价值为0。因此看涨期权到期日价值为“股票市价-执行价格”和“0”之间较大的一个。
多头看涨期权净损益=多头看涨期权到期日价值-期权价格
多头看涨期权的损益状况，如图6-1所示。
图6-1多头看涨期权
看涨期权损益的特点是÷净损失有限(最大值为期权价格)，而净收益却潜力巨大。那么，是不是投资期权一定比投资股票更好呢?不一定。例如，投资者有资金100元。投资方案一÷以5元的价格购人前述ABC公司的20股看涨期权。投资方案二÷购入ABC公司的股票1股。如果到期日股价为120元，购买期权的净损益=20x(120-100)-20x5=300(元)，报酬率=300÷100x100%=300%÷购买股票的净损益=120-100=20(元)，报酬率=20÷100x100%=20%。投资期权有巨大杠杆作用，因此对投机者有巨大的吸引力。如果股票的价格在此期间没有变化，购买期权的净收入为0，其净损失为100元；股票的净收入为100元，其净损失为0。股价无论下降得多么厉害，只要不降至0，股票投资者手里至少还有一股可以换一点钱的股票。期权投资者的风险要大得多，只要股价低于执行价格，无论低得多么微小，他们就什么也没有了，投入的期权成本全部损失了。

(二)卖出看涨期权

点击查看代码

看涨期权的出售者收取期权费，成为或有负债的持有人，负债的金额不确定。他处于空头状态，持有看涨期权空头头寸。
【例6-2】卖方售出1股看涨期权，其他数据与前例相同。标的股票的当前市价为100元，执行价格为100元，到期日为1年后的今天，期权价格为5元。其到期日的损益有以下四种可能：
(1)股票市价小于或等于100元，买方不会执行期权。由于期权价格为5元，空头看涨期权的净收益为5元(期权价格5元+期权到期日价值0元)。
(2)股票市价大于100元并小于105元，例如，股票市价为103元，买方会执行期权。卖方有义务以100元执行价格出售股票，需要以103元补进ABC公司的股票，他的净收入(即空头看涨期权到期日价值)为-3元(执行价格100元-股票市价103元)。空头看涨期权净收益为2元(期权价格5元+期权到期日价值-3元)。
(3)股票市价等于105元，期权买方会执行期权，空头净收入-5元(执行价格100元-股票市价105元)，空头看涨期权的净损益为0元(期权价格5元+期权到期日价值-5元)。
(4)股票市价大于105元，假设为110元，多头会执行期权，空头净收入-10元(执行价格100元-股票市价110元)。空头看涨期权净损益为-5元(期权价格5元+期权到期日价值-10元)
空头看涨期权到期日价值=-max(股票市价-执行价格，0)
空头看涨期权净损益=空头看涨期权到期日价值+期权价格
空头看涨期权的损益状况，如图6-2所示。对于看涨期权来说，空头和多头的到期日价值不同。如果标的股票价格高于执行价格，多头的到期日价值为正值，空头的到期日价值为负值，金额的绝对值相同。如果标的股票价格低于执行价格，期权被放弃，双方的到期日价值均为0。无论怎样，空头得到了期权费，而多头支付了期权费。

(三)买入看跌期权

点击查看代码

看跌期权买方拥有以执行价格出售股票的权利。
【例6-3】投资者持有执行价格为100元的看跌期权，到期日股票市价为80元，他可以执行期权，以80元的价格购入股票，同时以100元的价格售出，获得20元净收入。如果股票价格高于100元，他放弃期权，什么也不做，期权到期失效，他的净收入为0。
因此，到期日看跌期权买方损益可以表示为：
多头看跌期权到期日价值=max(执行价格-股票市价，0)
多头看跌期权净损益=多头看跌期权到期日价值-期权价格
图6-2空头看涨期权
看跌期权买方的损益状况，如图6-3所示。
图6-3多头看跌期权

(四)卖出看跌期权

点击查看代码

看跌期权的出售者收取期权费，成为或有负债的持有人，负债的金额不确定。
【例6-4】看跌期权出售者收取期权费5元，售出1股执行价格100元、1年后到期的ABC公司股票的看跌期权。如果1年后股价高于100元，期权持有人不会去执行期权，期权出售者的负债变为0。该头寸的最大利润是期权价格。如果情况相反，1年后股价低于100元，期权持有人就会执行期权，期权出售者必须依约按执行价格收购股票。该头寸的最大损失是执行价格减去期权价格。
因此，到期日看跌期权卖方损益可以表示为：
空头看跌期权到期日价值=-max(执行价格-股票市价，0)
空头看跌期权净损益=空头看跌期权到期日价值+期权价格
看跌期权卖方的损益状况如图6-4所示。
总之，如果标的股票的价格上涨，对于买入看涨期权和卖出看跌期权的投资者有利；如果标的股票的价格下降，对于卖出看涨期权和买人看跌期权的投资者有利。
图6-4空头看跌期权

三、期权的投资策略

前面我们讨论了单一股票期权的损益状态。买入期权的特点是最小的净收入为0，不会发生进一步的损失。因此，具有构造不同损益的功能。从理论上讲，期权可以帮助我们建立任意形式的损益状态，用于控制投资风险。这里只介绍三种投资策略。

(一)保护性看跌期权

点击查看代码

股票加多头看跌期权组合，是指购买1股股票，同时购入该股票的1股看跌期权。这种组合被称为保护性看跌期权。单独投资于股票风险很大，同时增加一股看跌期权，情况就会有变化，可以降低投资的风险。
【例6-5】购入1股ABC公司的股票，购入价格S=100元；同时购入该股票的1股看跌期权，执行价格X=100元，期权价格P=2.56元，1年后到期。在不同股票市场价格下的净收入和净损益如表6-5和图6-5所示。
表6-5保护性看跌期权的损益
微信截图_20240521080311.png
保护性看跌期权锁定了最低净收入(100元)和最低净损益(-2.56元)。但是，净损益的预期也因此降低了。上述四种情形下，投资于股票最好时能取得50元的净收益而投资于组合最好时只能取得47.44元的净收益。
图6-5保护性看跌期权

(二)抛补性看涨期权

点击查看代码

股票加空头看涨期权组合，是指购买1股股票，同时出售该股票的1股看涨期权。这种组合被称为抛补性看涨期权。抛出看涨期权所承担的到期出售股票的潜在义务，可以被组合中持有的股票抵补，不需要另外补进股票。
例6-6)依前例数据，购入1股ABC公司的股票，购入价格S=100元，同时出售该股票的1股看涨期权，期权价格C-5元，执行价格X=100元，1年后到期。在不同股票市场价格下的净收入和净损益如表6-6和图6-6所示。
表6-6
抛补性看涨期权的损益
图6-6抛补性看涨期权
抛补性看涨期权组合缩小了未来的不确定性。如果到期日股价超过执行价格，则锁定了净收入和净损益，净收入最多是执行价格(100元)，由于不需要补进股票也就锁定了净损益。相当于“出售”了超过执行价格部分的股票价值，换取了期权收入。如果到期日股价低于执行价格，净损失比单纯购买股票要小一些，减少的数额相当于期权价格。
抛补性看涨期权是机构投资者常用的投资策略。如果基金管理人计划在未来以100元的价格出售股票，以便套现分红，他现在就可以抛补看涨期权，赚取期权费。如果股价高于执行价格，他虽然失去了100元以上部分的额外收入，但是仍可以按计划取得100元现金。如果股价低于执行价格，还可以减少损失(相当于期权费收入)。因此，成为一个有吸引力的策略。

(三)对敲

对敲策略分为多头对敲和空头对敲。

1.多头对敲

点击查看代码

多头对敲是指同时买进一股股票的看涨期权和看跌期权，它们的执行价格、到期日都相同。
多头对敲策略对于预计市场价格将发生剧烈变动，但是不知道升高还是降低的投资者非常有用。例如，得知一家公司的未决诉讼将要宣判，如果该公司胜诉，预计股价将翻一番，如果败诉，预计股价将下跌一半。无论结果如何，多头对敲策略都会取得收益。
【例6-7】依前例数据，同时购入ABC公司股票的1股看涨期权和1股看跌期权。在不同股票市场价格下，多头对敲组合的净收入和净损益如表6-7和图6-7所示。
表6-7
多头对敲的损益
图6-7多头对敲
多头对敲的最坏结果是到期股价与执行价格一致，白白损失了看涨期权和看跌期权的购买成本。股价偏离执行价格的差额必须超过期权购买成本，才能给投资者带来净收益。

2.空头对敲

点击查看代码

空头对敲是指同时卖出一股股票的看涨期权和看跌期权，它们的执行价格、到期日都相同。
空头对敲策略对于预计市场价格将相对比较稳定的投资者非常有用。
【例6-8】依前例数据，同时卖出ABC公司股票的1股看涨期权和1股看跌期权。在不同股票市场价格下，空头对敲组合的净收入和净损益如表6-8和图6-8所示。
表6-8
空头对敲的损益
图6-8空头对敲
空头对敲的最好结果是到期股价与执行价格一致，投资者白白赚取出售看涨期权和看跌期权的收入。空头对敲的股价偏离执行价格的差额必须小于期权出售收入，才能给投资者带来净收益。

第三节金融期权价值评估

一、金融期权价值的影响因素

(一)期权的内在价值和时间溢价

期权价值由两部分构成÷即内在价值和时间溢价

1.期权的内在价值

点击查看代码

期权的内在价值，是指期权立即执行产生的经济价值。内在价值的大小，取决于期权标的资产的现行市价与期权执行价格的高低。内在价值不同于到期日价值，期权的到期日价值取决于到期日标的股票市价与执行价格的高低。如果现在已经到期，则内在价值与到期日价值相同。
对于看涨期权来说，现行资产价格高于执行价格时，立即执行期权能够给持有人带来净收入，其内在价值为现行价格与执行价格的差额(S-X)。如果资产的现行市价等于或低于执行价格时，立即执行不会给持有人带来净收入，持有人也不会去执行期权，此时看涨期权的内在价值为0。例如，看涨期权的执行价格为100元，现行价格为120元，其内在价值为20元(120-100)。如果现行价格变为80元，则内在价值为0。
对于看跌期权来说，现行资产价格低于执行价格时，其内在价值为执行价格减去现行价格(X-S)。如果资产的现行市价等于或高于执行价格，看跌期权的内在价值等于0。例如，看跌期权的执行价格为100元，现行价格为80元，其内在价值为20元(10080)。如果现行价格变为120元，则内在价值为0。
由于标的资产的价格是随时间变化的，所以内在价值也是变化的。当执行期权能给持有人带来正回报时，称该期权为“实值期权”，或者说它处于“实值状态”(溢价状态)；当执行期权将给持有人带来负回报时，称该期权为“虚值期权”，或者说它处于“虚值状态”(折价状态)；当资产的现行市价等于执行价格时，称期权为“平价期权”或者说它处于“平价状态”。
对于看涨期权来说，标的资产现行市价高于执行价格时，该期权处于实值状态；当资产的现行市价低于执行价格时，该期权处于虚值状态。对于看跌期权来说，资产现行市价低于执行价格时，该期权处于“实值状态”；当资产的现行市价高于执行价格时，该期权处于“虚值状态”
期权处于虚值状态或平价状态时不会被执行，只有处于实值状态才有可能被执行，但也不一定会被执行。
例如，20x2年4月3日，ABC公司股票的市场价格为79元。有1股看跌期权，执行价格为80元，20x2年6月到期，期权售价为4元，持有者可以在6月18日前的任意一天执行。如果持有人购买后立即执行，执行收入为1元(80-79)。期权发行时处于实值状态，或者说发行日是实值期权。此时，持有人并不会立即执行以获取1元收益，因为他花掉了4元钱成本，马上换回1元钱，并不划算。持有人购买看跌期权是预料将来股价会下跌，因此他会等待。只有到期日的实值期权才肯定会被执行，此时已不能再等待。

2.期权的时间溢价

点击查看代码

期权的时间溢价是指期权价值超过内在价值的部分。
时间溢价=期权价值-内在价值
例如，股票的现行价格为120元，看涨期权的执行价格为100元，期权价格为21元则时间溢价为1元(21-20)。如果现行价格等于或小于100元，则21元全部是时间溢价。
期权的时间溢价是一种等待的价值。期权买方愿意支付超出内在价值的溢价，是寄希望于标的股票价格的变化可以增加期权的价值。很显然，对于美式期权在其他条件不变的情况下，离到期时间越远，股价波动的可能性越大，期权的时间价也就越大。如果已经到期，期权的价值(价格)就只剩下内在价值(时间溢价为0)，因为已经不能再等待了。
期权处于虚值状态，仍然可以按正的价格售出，尽管其内在价值为0，但它还有时间溢价。在未来的一段时间里，如果价格上涨进入实值状态，投资者可以获得净收入；如果价格进一步下跌，也不会造成更多的损失，选择权为其提供了下跌保护。
时间溢价有时也称为期权的时间价值，但它和货币的时间价值是不同的概念。时间溢价是时间带来的波动的价值，是未来存在不确定性而产生的价值，不确定性越强，期权时间价值越大。而货币的时间价值是时间延续的价值，时间延续得越长，货币时间价值越大。

(二)影响期权价值的主要因素

点击查看代码

期权价值是指期权的现值，不同于期权的到期日价值。影响期权价值的因素主要有股票市价、执行价格、到期期限、股价波动率、无风险利率和预期红利。

1.股票市价

如果看涨期权在将来某一时间执行，其收入为股票价格与执行价格的差额。如果其他因素不变，随着股票市价的上升，看涨期权的价值也增加。看跌期权与看涨期权相反，看跌期权在未来某一时间执行，其收入是执行价格与股票价格的差额。如果其他因素不变，当股票市价上升时，看跌期权的价值下降。

2.执行价格

执行价格对期权价格的影响与股票市价相反。看涨期权的执行价格越高，其价值越小。看跌期权的执行价格越高，其价值越大。

3.到期期限

对于美式期权来说，较长的到期时间能增加看涨期权的价值。到期日离现在越远发生不可预知事件的可能性越大，股价变动的范围也越大。此外，随着时间的延长，行价格的现值会减少，从而有利于看涨期权的持有人，能够增加期权的价值。
对于欧式期权来说，较长的时间不一定能增加期权价值。虽然较长的时间可以降低执行价格的现值，但并不增加执行的机会。到期日价格的降低，有可能超过时间价值的差额。例如，两个欧式看涨期权，一个是1个月后到期，另一个是3个月后到期，预计标的公司两个月后将发放大量现金股利，股票价格会大幅下降，则有可能使时间长的期权价值低于时间短的期权价值。

4.股价波动率

股价波动率，是指股票价格变动的不确定性，通常用标准差衡量。股票价格的波动率越大，股价上升或下降的机会越大。对于股票持有者来说，两种变动趋势可以相互抵消，期望股价是其均值。对于看涨期权持有者来说，股价上升对其有利，股价下降对其不利，最大损失以期权费为限，两者不会抵消。因此，股价波动率增加会使看涨期权价值增加。对于看跌期权持有者来说，股价下降对其有利，股价上升对其不利，最大损失以期权费为限，两者不会抵消。因此，股价波动率增加会使看跌期权价值增加。在期权估值过程中，股价的波动性是最重要的因素。如果一种股票的价格波动性很小，其期权也值不了多少钱。
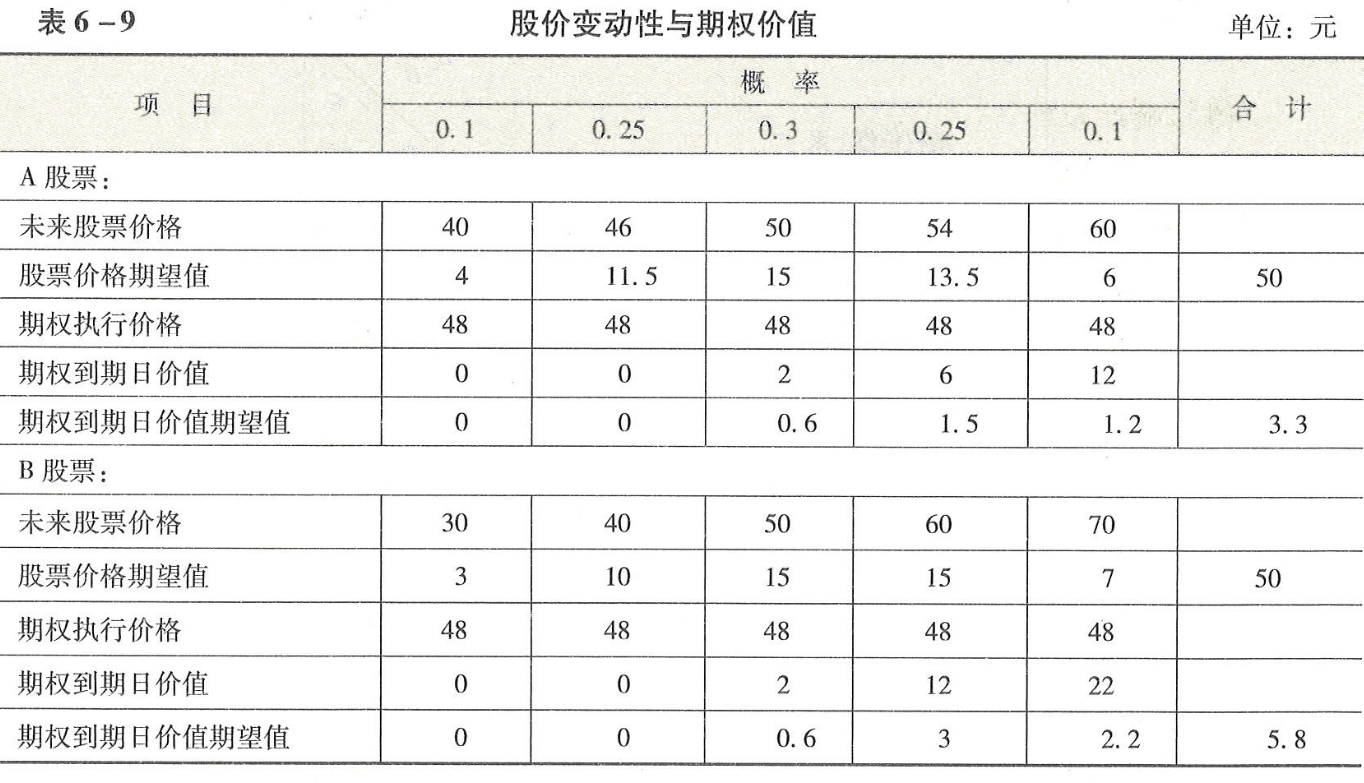
【例6-9】有A和B两种股票，其现行价格相同，未来股票价格的期望值也相同(50元)。以该股票为标的的看涨期权有相同的执行价(48元)，只要股价的变动性不同，期权价值就会有显著不同(见表6-9)。
这种情况说明，期权的价值并不依赖股票价格的期望值，而是股票价格的变动性(方差)。这是期权估值的基本原理之一。为便于理解，此处的举例说的是期权的“到期日价值”，对于期权的现值该原理仍然适用。
表6-9股价变动性与期权价值

微信截图_20240521080528.png

5.无风险利率

利率对于期权价格的影响是比较复杂的。一种简单而不全面的解释是÷假设股票价格不变，高利率会导致执行价格的现值降低，从而增加看涨期权的价值。还有一种理解的办法是÷投资于股票需要占用投资者一定的资金，投资于同样数量的该股票的看涨期权需要较少的资金。在高利率的情况下，购买股票并持有到期的成本越大，购买期权的吸引力越大。因此，无风险利率越高，看涨期权的价格越高。对于看跌期权来说，情况正好相反。

6.预期红利

在除息日后，红利的发放引起股票价格降低，看涨期权价格降低。与此相反，股票价格的下降会引起看跌期权价格上升。因此，看跌期权价值与预期红利大小呈正向变动而看涨期权价值与预期红利大小呈反向变动。
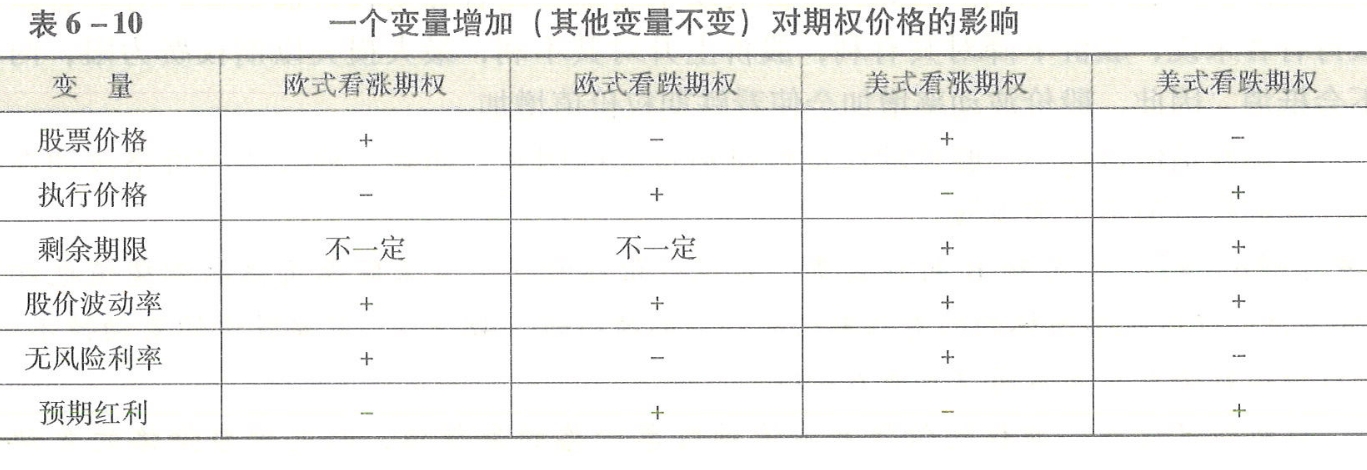
以上变量对于期权价格的影响如表6-10所示。
表6-10一个变量增加(其他变量不变)对期权价格的影响

微信截图_20240521080550.png
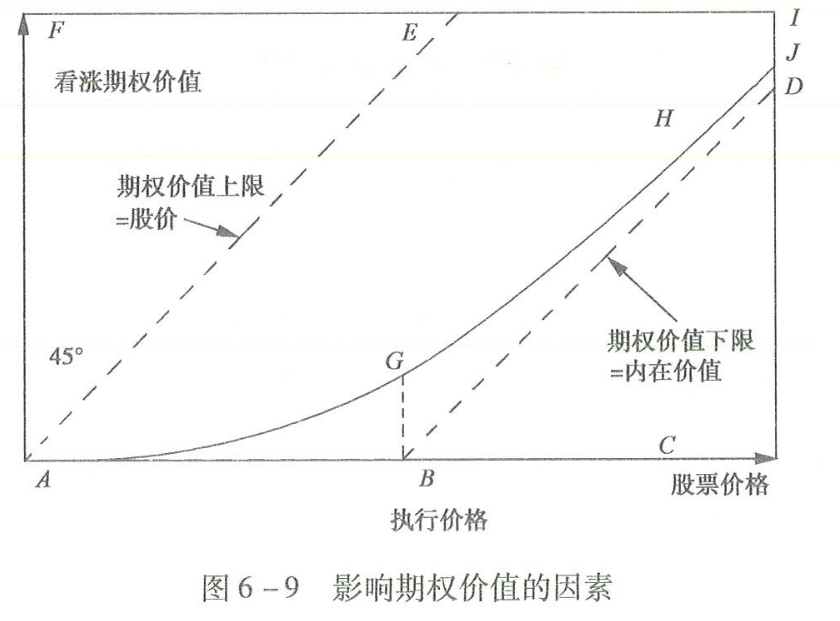
这些变量之间的关系如图6-9所示。

微信截图_20240521080608.png
图6-9影响期权价值的因素
在图6-9中，横坐标为股票价格，纵坐标为看涨期权(以下简称期权)价值；曲线AGH表示股票价格上升时期权价格也随之上升的关系，称为期权价值线；由点划线ABBD和AE围成的区域表示期权价值的可能范围，左侧点划线AE表示期权价值上限，右侧的点划线BD表示期权价值下限，下部的点划线AB表示股价低于执行价格时期权内在价值为0；左右两侧的点划线平行。
有关的含义说明如下：
(1)A点为原点，表示股票价格为0时，期权的价值也为0。为什么此时期权价值为0?股票价格为0，表明它未来没有任何现金流量，也就是将来没有任何价值。股票将来没有价值，期权到期时肯定不会被执行，即期权到期时将一文不值，所以期权的现值也为0。
(2)线段AB和BD组成期权的最低价值线。线段AB表示执行日股票价格低于执行价格(50元)，看涨期权不会执行，期权内在价值为0。线段BD表示执行日股票价格高于执行价格，看涨期权的内在价值等于股票价格与执行价格的差额。
在执行日之前，期权价值永远不会低于最低价值线。
为什么?例如，投资者有1股股票，今天的股价90元，若该股票的看涨期权价格定为39元(执行价格为50元)，小于立即执行的收入(40元)，投资者就可以卖出股票得到90元，用39元购买期权，然后执行期权花50元把股票买回来，投资者就可以净赚1元。这种套利活动，会使期权的需求上涨，回升到右侧的点划线BD的D点上方(例如J点)。
(3)左侧的点划线AE是期权价值上限。在执行日，股票的最终收入总要高于期权的最终收入。例如，假设看涨期权的价格等于股价，甲用40元购人1股股票，乙用40元购人该股票的1股看涨期权(执行价格50元)；如果到期日股票价格高于执行价格(假设股价为60元)，乙会借人50元执行期权，并将得到的股票出售，还掉借款后手里剩10元；甲出售股票，手中有60元(高于乙)。如果到期日股票价格为49元，乙会放弃期权，手中一无所有；甲出售股票，手中有49元(高于乙)。这就是说，期权价格如果等于股票价格，无论未来股价高低(只要它不为0)，购买股票总比购买期权有利。在这种情况下，投资者必定抛出期权，购入股票，迫使期权价格下降。所以，看涨期权的价值上限是股价。
(4)曲线AGJ是期权价值线。期权价值线从A点出发后，呈一弯曲线向上，逐渐与BD趋于平行。该线反映股价和期权价值的关系，期权价值随股票价格上涨而上涨。
除原点外，期权价值线(AGJ)必定会在最低价值线(ABD)的上方。只要股价大于0，期权价值必定会高于最低价值线对应的最小价值。为什么这样说呢?观察点÷今天股价等于执行价格，如果执行则收入为0。此时无法预计未来执行日的股价，可以假设有50%的可能会高于执行价格，另有50%的可能会低于执行价格。那么，有50%的可能股价上涨，执行期权则收入为股价减50元的差额÷另有50%的可能股价下降放弃期权则收入为0。因此，产生正的收入的概率大于0，最坏的结果是收入为0，期权肯定有价值。这就是说，只要尚未到期，期权的价格就会高于其价值下限。
(5)股价足够高时，期权价值线与最低价值线的上升部分逐步接近。
股价越高，期权被执行的可能性越大。股价高到一定程度，执行期权几乎是可以肯定的，或者说，股价再下降到执行价格之下的可能性已微乎其微。此时，期权持有人已经知道他的期权将被执行，可以认为他已经持有股票，唯一的差别是尚未支付执行所需的款项。该款项的支付，可以推迟到执行期权之时。在这种情况下，期权执行几乎是肯定的，而且股票价值升高，期权的价值也会等值同步增加。

二、金融期权价值的评估方法

点击查看代码

从20世纪50年代开始，现金流量折现法成为资产估值的主流方法，任何资产的价值都可以用其预期未来现金流量的现值来估值。现金流量折现法估值的基本步骤是÷首先预测资产的期望现金流量；其次，估计投资的必要报酬率；最后，用必要报酬率折现现金流量。人们曾力图使用现金流量折现法解决期权估值问题，但是一直没有成功。问题在于期权的必要报酬率非常不稳定。期权的风险依赖于标的资产的市场价格，而市场价格是随机变动的，期权投资的必要报酬率也处于不断变动之中。既然找不到一个适当的折现率，现金流量折现法也就无法使用。因此，必须开发新的模型，才能解决期权定价问题。
1973年，布莱克-斯科尔斯期权定价模型被提出，人们终于找到了实用的期权定价方法。此后，期权市场和整个衍生金融工具交易飞速发展。由于对期权定价问题研究的杰出贡献，斯科尔斯和默顿获得1997年诺贝尔经济学奖。
如果没有足够的数学背景知识，要全面了解期权定价模型是非常困难的。出于本教材的目的，不打算全面介绍期权估值模型，而主要通过举例的方法介绍期权估值的基本原理和主要模型的使用方法。

(一)期权估值原理

1.复制原理

复制原理的基本思想是

构造一个股票和借款的适当组合，使得无论股价如何变动投资组合的损益都与期权相同，那么，创建该投资组合的成本就是期权的价值。

下面我们通过一个假设的简单举例，说明复制原理。
【例6-10】假设ABC公司的股票现在的市价为50元。有1股以该股票为标的资产的看涨期权，执行价格为52.08元，到期时间是6个月。6个月以后股价有两种可能÷上升33.33%，或者下降25%，无风险利率为每年4%。拟建立一个投资组合，包括购进适量的股票以及借入必要的款项，使得该组合6个月后的价值与购进该看涨期权相等，

可以通过下列过程来确定该投资组合：

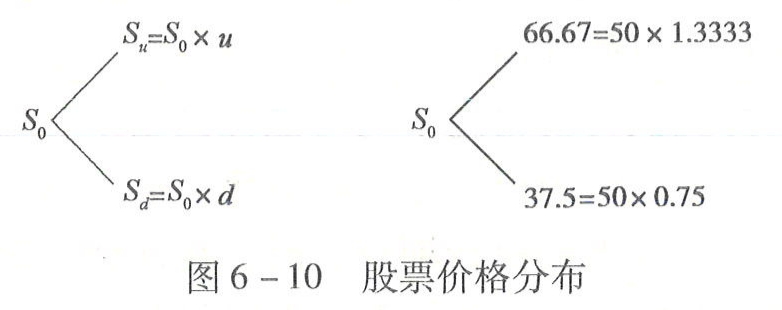
(1)确定6个月后可能的股票价格。假设股票当前价格为S，未来变化有两种可能÷上升后股价S和下降后股价S。为便于用当前价格表示未来价格，设÷S=uxSo，u称为股价上行乘数；S=dxS，d为股价下行乘数。用二叉树图形表示的股价分布如图6-10所示，图的左侧是一般表达式，右侧是将[例6-10]的数据代入的结果。其中，S=50元，u=1.3333，d=0.75。

微信截图_20240521080655.png
图6-10股票价格分布
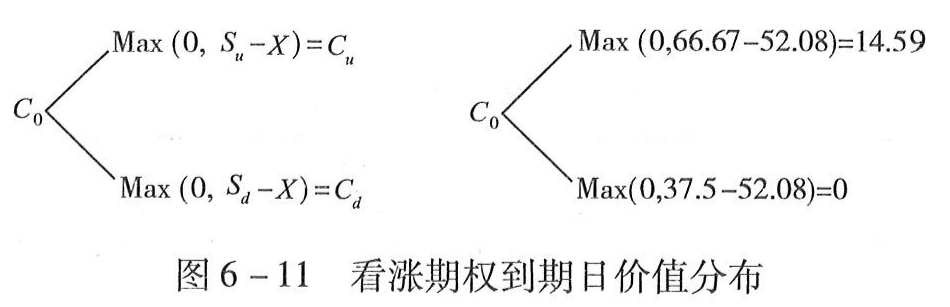
(2)确定看涨期权的到期日价值。由于执行价格X=52.08元，到期日看涨期权的价值如图6-11所示。左边是一般表达式，右边是代入本例数据后的结果。

微信截图_20240521080712.png
图6-11看涨期权到期日价值分布
(3)建立对冲组合。上面我们已经知道了期权的到期日价值有两种可能÷股价上行时为14.59元，股价下行时为0元。已知借款的利率为2%(半年)。我们要复制一个股票与借款的投资组合，使之到期日的价值与看涨期权相同。
该投资组合为÷购买0.5股的股票，同时，以2%的利率借入18.38元。这个组合的收入同样也依赖于期末股票的价格，如表6-11所示。
表6-11投资组合的收入

微信截图_20240521080730.png
该组合的到期日净收入分布与购入看涨期权一样。因此，看涨期权的价值应当与建立投资组合的成本一样。
组合投资成本=购买股票支出-借款=50x0.5-18.38=6.62(元)
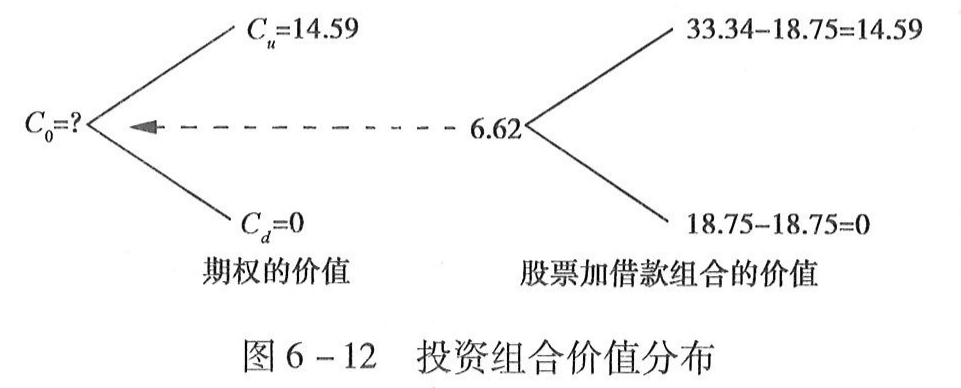
因此，该看涨期权的价格应当是6.62元(见图6-12)。

微信截图_20240521080744.png
图6-12投资组合价值分布

2.套期保值原理

点击查看代码

在看了[例6-10]之后，可能会产生一个疑问÷如何确定复制组合的股票数量和借款数量，使投资组合的到期日价值与期权相同。
这个比率称为套期保值比率(或称套头比率、对冲比率、德尔塔系数)，我们用H来表示。

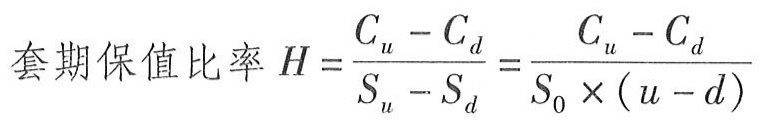
微信截图_20240521080756.png
该公式可以通过以下方法证明：
既然「例6-10]中的两个方案在经济上是等效的，那么，购入0.5股股票，同时，卖空1股看涨期权，就应该能够实现完全的套期保值。可以通过表6-12加以验证。
表6-12股票和卖出看涨期权

微信截图_20240521080810.png
无论到期日的股票价格是多少，该投资组合得到的净现金流量都是一样的。只要股票和期权的比例配置适当，就可以使风险完全对冲，锁定组合的现金流量。可见，股票和期权的比例取决于它们的风险是否可以实现完全对冲。
根据到期日股价上行时的现金净流量等于股价下行时的现金净流量可知：

微信截图_20240521080825.png
由于看涨期权在股价下跌时不会被执行，因此组合的现金流量仅为股票的收入，在归还借款后组合的最终现金流量为0。
下面再回顾「例6-10]的解题过程：
(1)确定可能的到期日股票价格。

微信截图_20240521080839.png

3.风险中性原理

点击查看代码

从上面的例子可以看出，运用财务杠杆投资股票来复制期权是很麻烦的。[例6-10]是一个再简单不过的期权，如果是复杂期权或涉及多个期间，复制就成为令人苦恼的工作。好在有一个替代办法，不需要每一步计算都复制投资组合，它被称为风险中性原理。
所谓风险中性原理，是指假设投资者对待风险的态度是中性的，所有证券的预期报酬率都应当是无风险利率。风险中性的投资者不需要额外的收益补偿其承担的风险。在风险中性的世界里，将期望值用无风险利率折现，可以获得现金流量的现值。
在这种情况下，期望报酬率应符合下列公式：

微信截图_20240521080857.png
期权定价以套利理论为基础。如果期权的价格高于6.62元，就会有人购入0.5股股票，卖出1股看涨期权，同时借入18.38元，肯定可以盈利。如果期权价格低于6.62元就会有人卖空0.5股股票，买入1股看涨期权，同时借出18.38元，也肯定可以盈利。因此，只要期权定价不是6.62元，市场上就会出现一台“造钱机器”。套利活动会促使期权只能定价为6.62元。

(二)二叉树期权定价模型

1.单期二叉树定价模型

(1)二叉树模型的假设

二叉树期权定价模型建立在以下假设基础之上

①市场投资没有交易成本；②投资者都是价格的接受者；③允许完全使用卖空所得款项；④允许以无风险利率借人或贷出款项；⑤未来股票的价格将是两种可能值中的一个。

(2)单期二叉树公式的推导。

点击查看代码

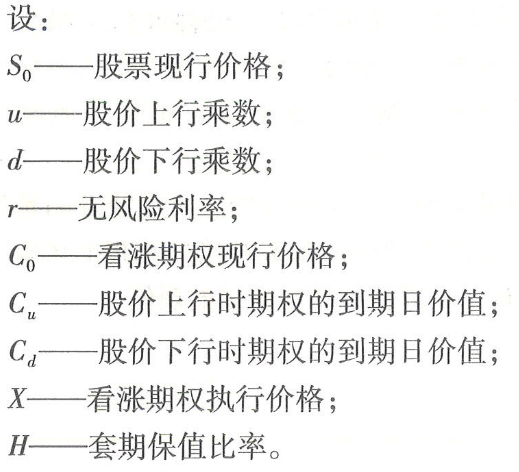
二叉树模型的推导始于建立一个投资组合÷①一定数量的股票多头头寸；②该股票的看涨期权的空头头寸。股票的数量要使头寸足以抵御资产价格在到期日的波动风险，即该组合能实现完全套期保值，产生无风险利率，即应用上文期权估值的套期保值原理。

微信截图_20240521080928.png

微信截图_20240521080946.png
根据公式直接计算「例6-10]的期权价格如下：

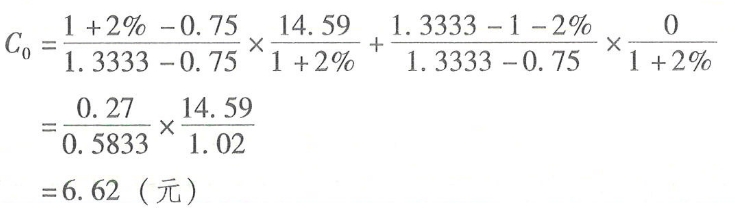
微信截图_20240521080958.png
可以利用「例6-10]的数据回顾一下公式的推导思路÷最初，投资于0.5股股票需要投资25元；收取6.62元的期权价格，尚需借入18.38元资金。半年后如果股价涨到66.67元，投资者0.5股股票收入33.33元；借款本息为18.75元(18.38x1.02)，看涨期权持有人会执行期权，期权出售人补足价差14.59元(66.67-52.08)，投资者的净损益为0。半年后如果股价跌到37.5元，投资者0.5股股票收入18.75元÷支付借款本息18.75元，看涨期权持有人不会执行期权，期权出售人没有损失，投资者的净损益为0。因此，该看涨期权的公平价值就是6.62元。

2.两期二叉树模型

点击查看代码

单期的定价模型假设未来股价只有两个可能，对于时间很短的期权来说是可以接受的。若到期时间很长，如[例6-10]的半年时间，就与事实相去甚远。改善的办法是把到期时间分割成两部分，每期3个月，这样就可以增加股价的选择。还可以进一步分割，如果每天为一期，情况就好多了。如果每个期间无限小，股价就成了连续分布，布莱克斯科尔斯模型就诞生了。
简单地说，由单期模型向两期模型的扩展，不过是单期模型的重复应用，任何一次应用均可使用上文的三种原理中的任何一个。

【例6-11】继续采用「例6-10]中的数据，把6个月的时间分为两期，每期3个月。变动以后的数据如下÷ABC公司的股票现在的市价为50元，看涨期权的执行价格为52.08元，每期股价有两种可能÷上升22.56%或下降18.4%÷无风险利率为每3个月1%

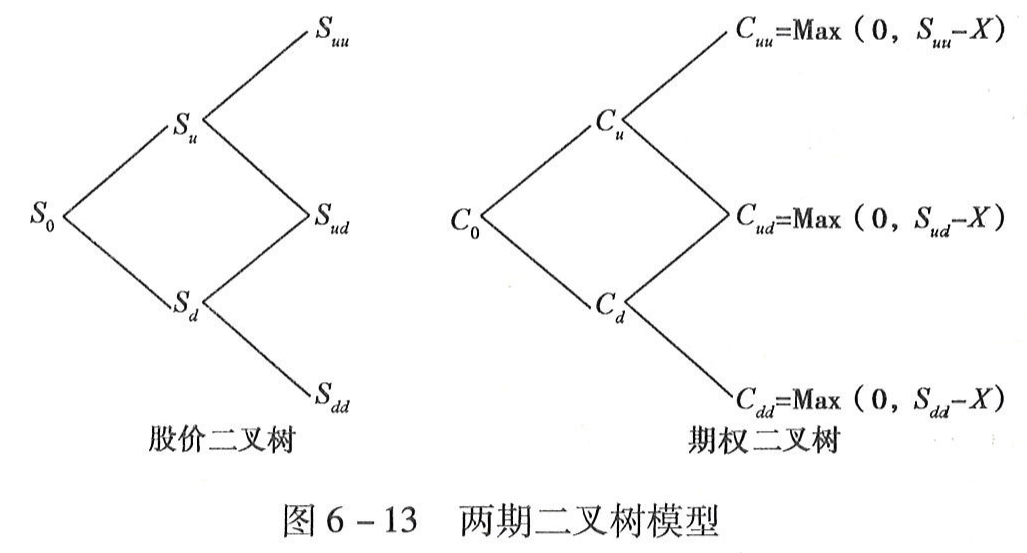
为了直观地显示有关数量的关系，仍然使用二又树图示。两期二叉树的一般形式如图6-13所示。将[例6-11]中的数据填入后如图6-14所示。

微信截图_20240521081644.png
图6-13两期二叉树模型

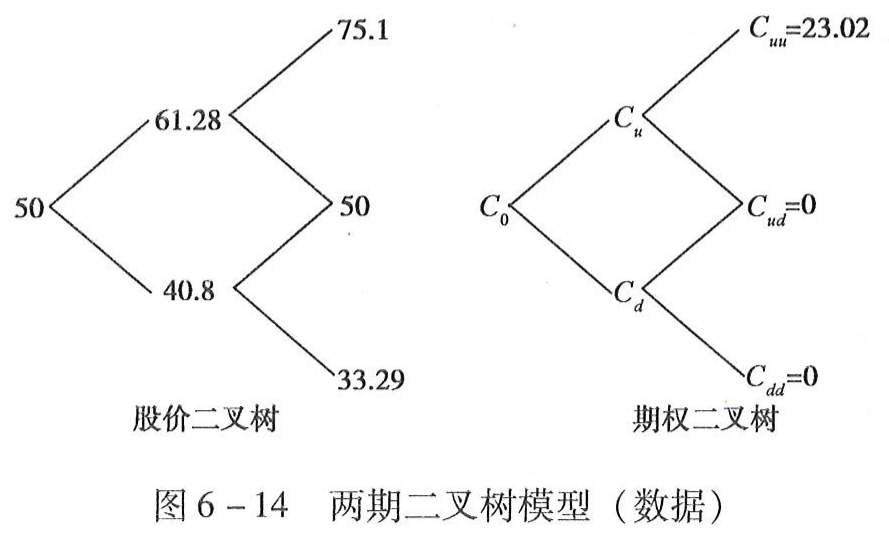
微信截图_20240521081654.png
图6-14两期二叉树模型(数据)
解决问题的办法是÷先利用单期定价模型，根据Cuu和Cud计算Cu的价值，利用Cud和Cdd计算Cd的价值；然后，再次利用单期定价模型，根据Cu和Cd计算C0的价值。从后向前推进。

下面，分别以应用期权估值的复制原理和风险中性原理为例，解决两期二叉树模型下的期权估值问题。

(1)应用复制原理：

点击查看代码

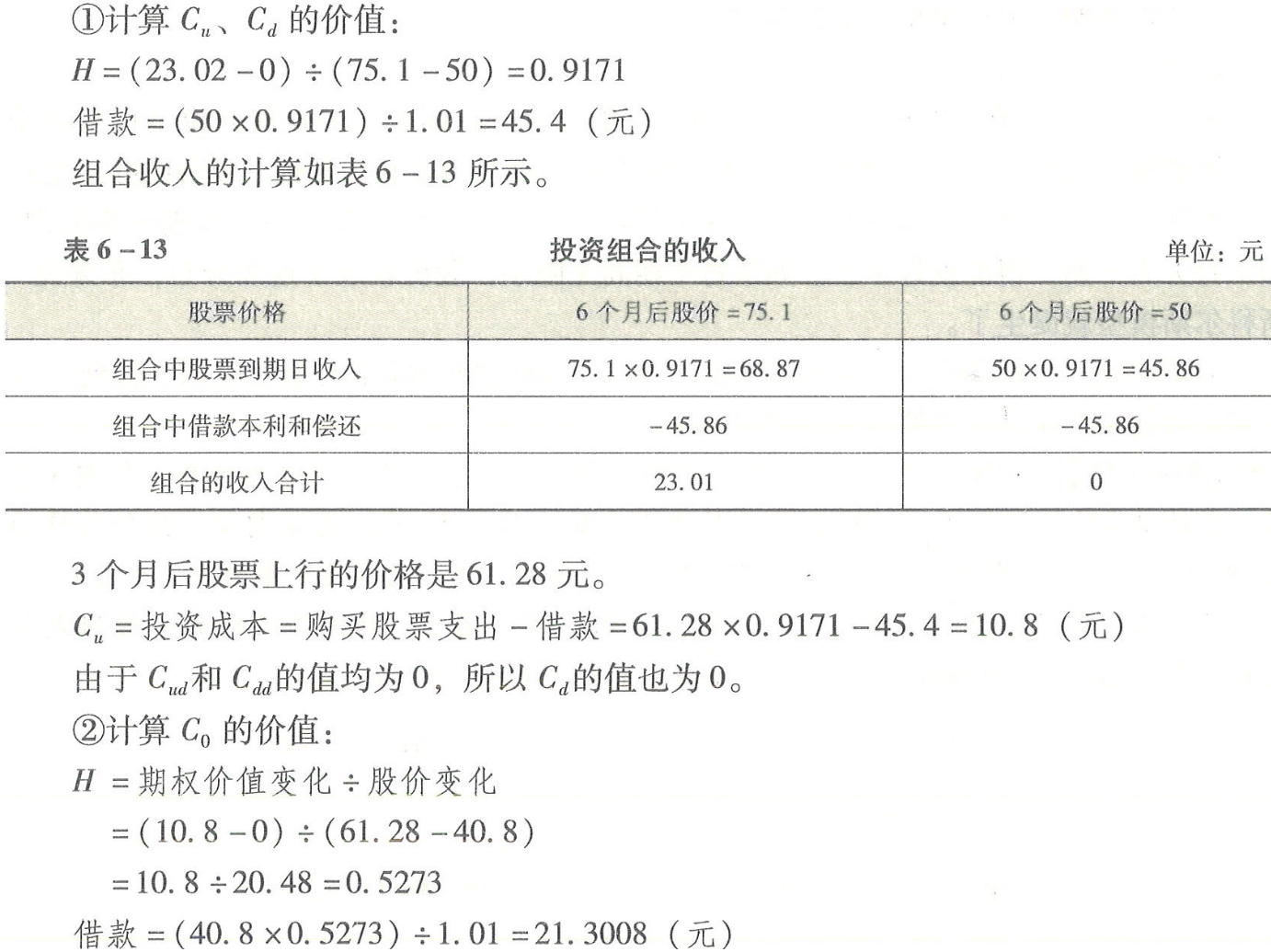
微信截图_20240521081758.png
组合收入的计算如表6-14所示。
表6-14投资组合的收入

微信截图_20240521081819.png

微信截图_20240521081828.png

(2)应用风险中性原理：

点击查看代码

微信截图_20240521081836.png

微信截图_20240521081852.png

3.多期二叉树模型

点击查看代码

如果继续增加分割的期数，就可以使期权价值更接近实际。从原理上看，与两期模型一样，从后向前逐级推进，只不过多了一个层次。期数增加以后带来的主要问题是股价上升与下降的百分比如何确定问题。期数增加以后，要调整价格变化的升降幅度，以保证年报酬率的标准差不变。把年报酬率标准差和升降百分比联系起来的公式是：

微信截图_20240521081905.png
[例6-10]采用的标准差σ=0.4068，

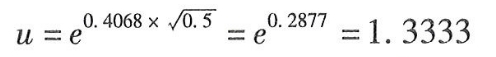
微信截图_20240521081915.png
该数值可以利用函数计算器直接求得，或者使用Excel的EXP函数功能，输入0.2877，就可以得到以e为底、指数为0.2877的值为1.3333。
d=1÷1.3333=0.75
如果间隔期为1/4年，u=1.2256即上升22.56%，d=0.816即下降18.4%，这正是我们在「例6-11]中采用的数据；如果间隔期为1/6年，u=1.1807即上升18.07%d=0.847即下降15.3%；如果间隔期为1/52年，u=1.058即上升5.8%，d=0.945即下降5.5%；如果间隔期为1/365年，u=1.0215即上升2.15%，d=0.979即下降2.1%。

【例6-12】沿用[例6-10]中的数据，将半年的时间分为6期，即每月1期。已知÷股票价格S=50元，执行价格为52.08元，年无风险利率为4%，股价波动率(标准差)为0.4068，到期时间为6个月，划分期数为6期(即每期1个月)

点击查看代码

(1)确定每期股价变动乘数。
微信截图_20240521081950.png
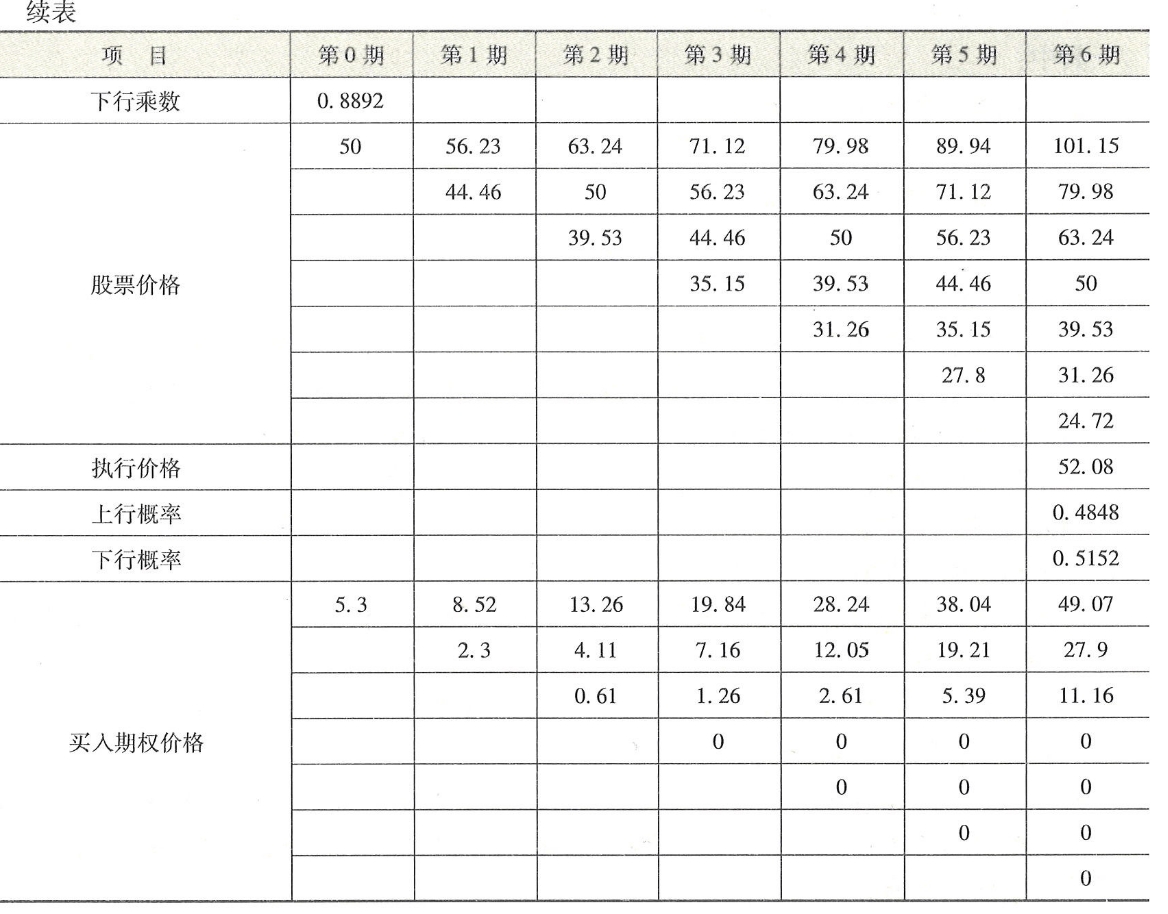
(2)建立股票价格二叉树(见表6-15中的“股票价格”部分)。
第一行从当前价格50元开始，以后是每期上升12.46%的价格路径，6期后为101.15元。第二行为第1期下降，第2~6期上升的路径。以下各行以此类推。这种二叉树与图6-14只是形式不同，目的是便于在Excel表中计算。
(3)根据股票价格二叉树和执行价格，构建期权价值的二叉树(见表6-15中的“买入期权价格”部分)。
构建顺序为由后向前，逐级推进。
①确定第6期的各种价格下的期权价值：
微信截图_20240521082010.png
以下4项的股票价格均低于或等于执行价格，所以期权价值为0。
②确定第5期的期权价值：
微信截图_20240521082027.png
③确定期权的现值：
期权现值=(8.52x0.4848+2.3x0.5152)÷(1+4%÷12)=5.3(元)
表6-15
股票期权的6期二叉树

微信截图_20240521082041.png

微信截图_20240521082051.png

二叉树方法是一种近似的方法。不同的期数划分，可以得到不同的近似值。期数越多，计算结果与布莱克-斯科尔斯定价模型的计算结果差额越小。

(三)布莱克-斯科尔斯期权定价模型

点击查看代码

布莱克-斯科尔斯期权定价模型(简称BS模型)是理财学中最复杂的公式之一，其证明和推导过程涉及复杂的数学问题，但使用起来并不困难。该公式有非常重要的意义它对理财学具有广泛的影响，是近代理财学不可缺少的内容。该模型具有实用性，被期权交易者广泛使用，实际的期权价格与模型计算得到的价格非常接近。

1.布莱克-斯科尔斯模型的假设

点击查看代码

(1)在期权寿命期内，期权标的股票不发放股利，也不做其他分配
(2)股票或期权的买卖没有交易成本；
(3)短期的无风险利率是已知的，并且在期权寿命期内保持不变；
(4)任何证券购买者都能以短期的无风险利率借得任何数量的资金；
(5)允许卖空，卖空者将立即得到所卖空股票当天价格的资金；
(6)看涨期权只能在到期日执行：
(7)所有证券交易都是连续发生的，股票价格随机游走

2.布莱克-斯科尔斯模型

布莱克-斯科尔斯模型的公式如下：

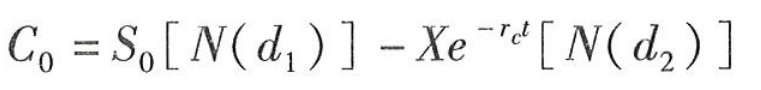
微信截图_20240521082117.png

微信截图_20240521082135.png
如果直观(不准确)地解释，它的第一项是最终股票价格的期望现值，第二项是期权执行价格的期望现值，两者之差是期权的价值。

微信截图_20240521082149.png

【例6-13】沿用[例6-10]的数据，某股票当前价格为50元，执行价格为52.08元，期权到期日前的时间为0.5年。每年复利一次的无风险利率为4%，相当连续复利的无风险利率\(r=ln(1.04)=3.9221%\)，连续复利的标准差\(σ=0.4068\)，即方差\(o’=0.1655\)。

根据以上资料计算期权价格如下：

微信截图_20240521082206.png

微信截图_20240521082218.png
根据[例6-10]的资料，采用单期二叉树模型计算的期权价值是6.62元，采用两期二叉树模型计算的期权价值是5.06元，采用6期二叉树模型计算的期权价值是5.3元采用BS模型计算的期权价值是5.26元。随着二叉树模型设置期数的增加，其计算结果不断逼近BS模型。

通过该模型可以看出，决定期权价值的因素有五个

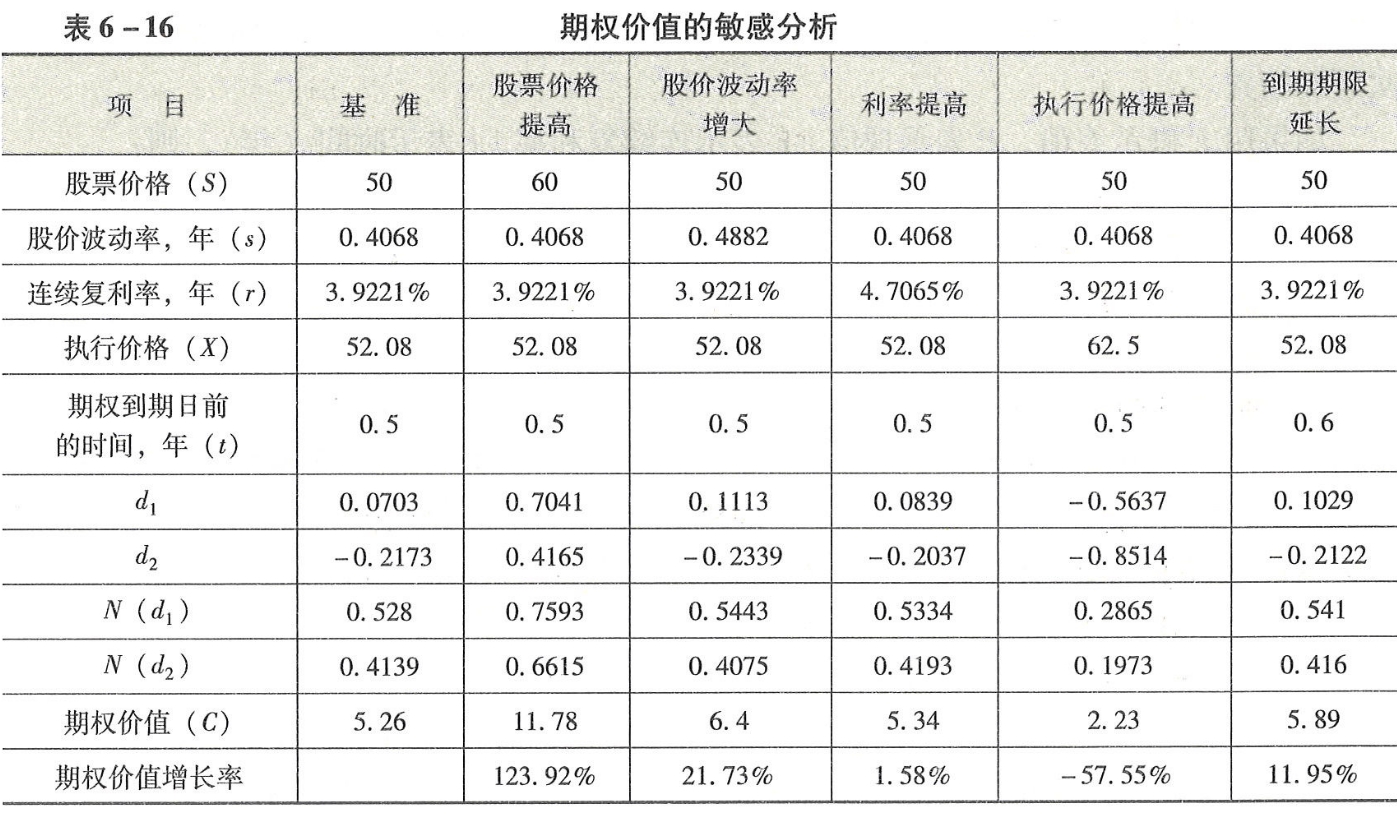
÷股票价格、股价波动率、利率执行价格和期权到期日前的时间。它们对于期权价值的影响，可以通过敏感分析表来观察(见表6-16)。
表6-16期权价值的敏感分析

微信截图_20240521082233.png
(1)股票价格÷如果当前股票价格提高20%，由50元提高到60元，则期权价值由5.26元提高到11.78元，提高123.92%。可见，期权价值的增长率大于股价增长率。
(2)股价波动率÷如果标准差提高20%，则期权价值提高21.73%。可见，标的股票的风险越大，期权的价值越大。
(3)利率÷如果利率提高20%，则期权价值提高1.58%。可见，虽然利率的提高有助于期权价值的提高，但是期权价值对于无风险利率的变动并不敏感。
(4)执行价格÷如果执行价格提高20%，则期权价值降低57.55%。可见，期权价值的变化率大于执行价格的变化率。值得注意的是，此时期权价值的下降额3.03元(5.26-2.23)小于执行价格的上升额10.42元(62.5-52.08)。
(5)期权到期日前的时间÷如果期权到期日前的时间由0.5年延长到0.6年，则期权价值由5.26元提高到5.89元。

3.模型参数的估计

点击查看代码

布莱克-斯科尔斯模型有5个参数。其中，现行股票价格和执行价格容易取得。至到期日的剩余年限计算，一般按自然日(1年365天或为简便用360天)计算，易于确定但无风险利率和股票报酬率的标准差，难以估计。

(1)无风险利率的估计。

点击查看代码

无风险利率应当用无违约风险的固定证券收益来估计，例如政府债券的利率。政府债券的到期时间不等，其利率也不同。应选择与期权到期日相同的政府债券利率，例如期权还有3个月到期，就应选择3个月到期的政府债券利率。如果没有相同时间的，应选择时间最接近的政府债券利率。
这里所说的政府债券利率是指其市场利率，而不是票面利率。政府债券的市场利率是根据市场价格计算的到期报酬率。再有，模型中的无风险利率是指按连续复利计算的利率，而不是常见的年复利。由于布莱克-斯科尔斯模型假设套期保值率是连续变化的因此，利率要使用连续复利。连续复利假定利息是连续支付的，利息支付的频率比每秒1次还要频繁。
如果用F表示终值，P表示现值，\(r_c\)表示连续复利率，t表示时间(年)，则：

微信截图_20240521082308.png
自然对数的值，很容易在具有函数功能的计算器上计算求得，或者利用“自然对数表”(见本书附表五)查找，也可以利用Excel的LN数功能求得。\(e^{r_c*t}\)为连续复利的终值系数，可利用“连续复利终值系数表”(见本书附表六)查找。

【例6-14】假设t=1年，F=104元，P=100元，则：

点击查看代码

\(r_c=In(104÷100)÷1=In(1.04)÷1=3.9221%\)
严格来说，期权估值中使用的利率都应当是连续复利，包括二叉树模型和BS模型即使在资本预算中，使用的折现率也应当是连续复利率，因为全年收入和支出总是陆续发生的，只有连续复利率才能准确完成终值和现值的折算。在使用计算机运算时，采用连续复利通常没有什么困难，但是手工计算则比较麻烦。为了简便，手工计算时往往使用分期复利作为连续复利的近似替代。由于期权价值对于利率的变化并不敏感，因此这种简化通常是可以接受的。
使用分期复利时也有两种选择÷①按有效年利率折算。例如，有效年利率为4%，则等价的半年利率为√(1+4%)-1=1.98%。②按报价利率折算。例如，报价利率为4%则半年利率为4%÷2=2%。

(2)报酬率标准差的估计。

点击查看代码

股票报酬率的标准差可以使用历史报酬率来估计。计算连续复利标准差的公式与年复利相同：

微信截图_20240521082429.png
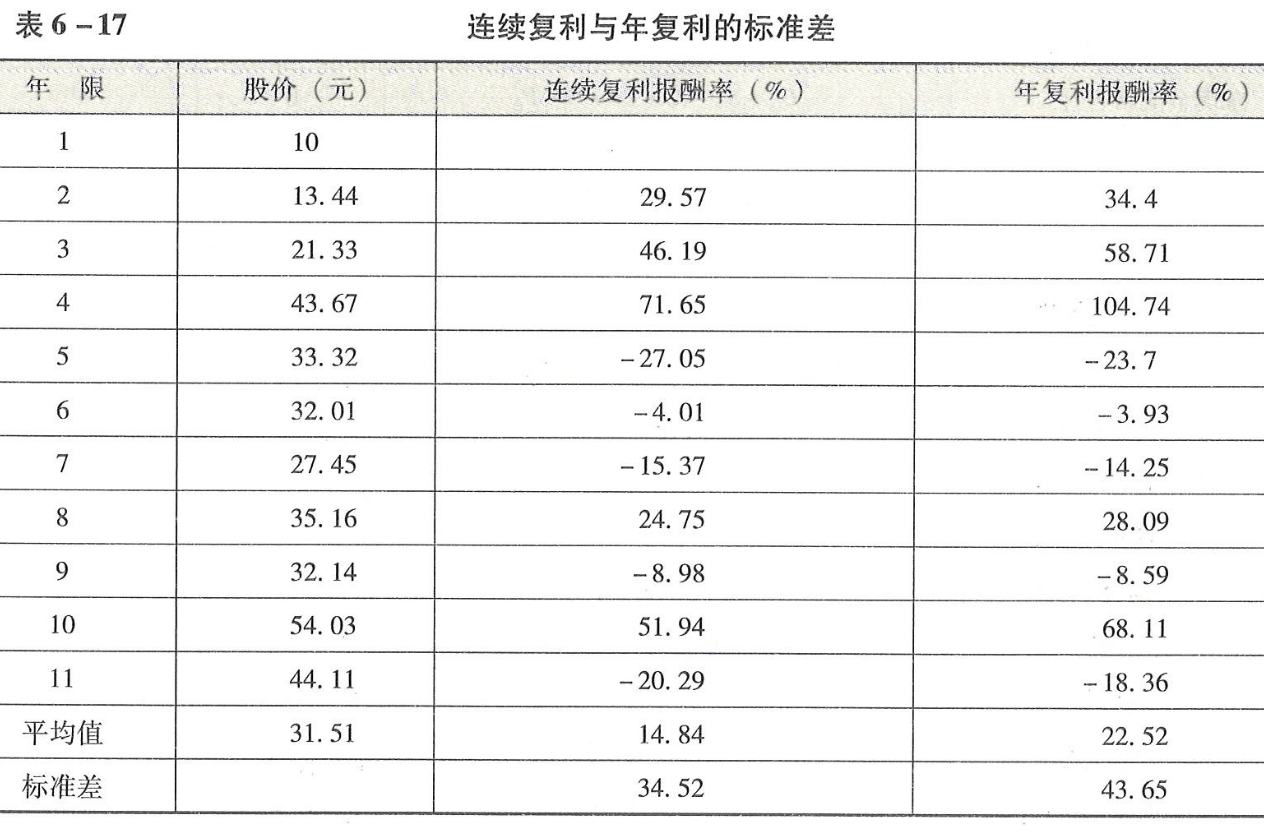
[例6-15]ABC公司过去11年的股价如表6-17第2列所示，假设各年均没有发放股利，据此计算的连续复利报酬率和年复利报酬率如第3列和第4列所示。
表6-17连续复利与年复利的标准差

微信截图_20240521082443.png
在期权估值中，严格说来应当使用连续复利报酬率的标准差。有时为了简化，也可以使用分期复利报酬率的标准差作为替代。

4.看跌期权估值

前面的讨论主要针对看涨期权，那么，如何对看跌期权估值呢?

在套利驱动的均衡状态下，看涨期权价格、看跌期权价格和股票价格之间存在一定的依存关系。对于欧式期权，假定看涨期权和看跌期权有相同的执行价格和到期日，则下述等式成立：
看涨期权价格C-看跌期权价格P=标的资产价格S-执行价格现值PV(X)
这种关系被称为看涨期权-看跌期权平价定理(关系)。利用该定理，已知等式中的4个数据中的3个，就可以求出另外1个。
C=S+P-PV(X)
P=-S+C+PV(X)
S=C-P+PV(X)
PV(X)=S-C+P
该公式的有效性，可以通过表6-18验证
表6-18
看涨和看跌期权的平价关系

【例6-16】两种期权的执行价格均为30元，6个月到期，6个月的无风险利率为4%，股票的现行价格为35元，看涨期权的价格为9.2元，则看跌期权的价格为：

点击查看代码

P=-S+C+PV(X)
=-35+9.2+30÷(1+4%)
=-35+9.2+28.8
=3(元)

5.派发股利的期权定价

点击查看代码

布莱克-斯科尔斯期权定价模型假设在期权寿命期内买方期权标的股票不发放股利那么在标的股票派发股利的情况下应如何对期权估值呢?
股利的现值是股票价值的一部分，但是只有股东可以享有该收益，期权持有人不能享有。因此，在期权估值时要从股价中扣除期权到期日前所派发的全部股利的现值。也就是说，把所有到期日前预期发放的未来股利视同已经发放，将这些股利的现值从现行股票价格中扣除。此时，模型建立在调整后的股票价格而不是实际价格基础上。
考虑派发股利的期权定价公式如下：

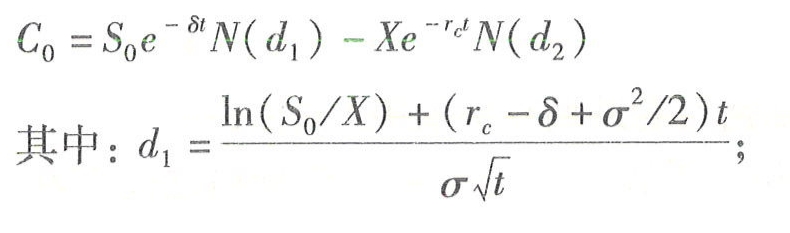
微信截图_20240521082525.png

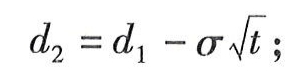
微信截图_20240521082535.png
8表示标的股票的年股利报酬率(假设股利连续支付，而不是离散分期支付)。
如果标的股票的年股利报酬率σ为0，则与前面介绍的布莱克-斯科尔斯模型相同。

6.美式期权估值

布莱克-斯科尔斯期权定价模型假设看涨期权只能在到期日执行，即模型仅适用于欧式期权，那么，美式期权如何估值呢?

美式期权在到期前的任意时间都可以执行，除享有欧式期权的全部权利之外，还有提前执行的优势。因此，美式期权的价值应当至少等于相应欧式期权的价值，在某种情况下比欧式期权的价值更大。

第四节实物期权价值评估

点击查看代码

实物资产投资与金融资产投资不同。大多数投资者一旦购买了证券，只能被动地等待而无法影响它所产生的现金流；投资于实物资产则不同，投资者可以通过管理行动影响它所产生的现金流。也就是说，实物资产投资在执行过程中可能会出现许多新变化和新机会，给投资者带来经营灵活性。这些经营灵活性嵌入在投资项目中，通常可以增加项目投资者的选择权，对于项目价值评估或资本预算具有革命性的影响。由于这些选择权是以实物资产为标的资产，是未来可以采取某种行动的权利而非义务，因此被称为实物期权(real-option)。
在应用现金流量折现法评估项目价值时，我们通常假设公司会按既定的方案执行不会在执行过程中进行重要的修改。实际上，管理者会随时关注各种变化，如果事态表明未来前景比当初设想得更好，管理者会加大投资力度，反之则会设法减少损失。只要未来是不确定的，管理者就会利用拥有的实物期权增加价值，而不是被动地接受既定方案。完全忽视项目本身的实物期权，是传统现金流量折现法的局限性。事实上，折现现金流量往往不能提供一个项目价值的全部信息，仅仅依靠现金流量折现法有时会导致错误的资本预算决策。如果考虑实物期权的价值，那么净现值为负值的项目也有可能被接受，而不是被断然拒绝。
实物期权隐含在投资项目中，一个重要的问题是将其识别出来。并不是所有项目都含有值得重视的期权，有的项目期权价值很小，有的项目期权价值很大。这要看项目不确定性的大小，不确定性越大，则期权价值越大。本节主要讨论三种常见的实物期权：扩张期权、延迟期权和放弃期权。
实物期权估价使用的模型主要是BS模型和二叉树模型。通常BS模型是首选模型它的优点是使用简单并且计算精确。它的应用条件是实物期权的情景符合BS模型的假设条件，或者说该实物期权与典型的股票期权相似。二叉树模型是一种替代模型。它虽然没有BS模型精确，但是比较灵活，在特定情景下优于BS模型。二叉树模型可以根据特定项目模拟现金流的情景，使之适用于各种复杂情况。例如，处理到期日前支付股利的期权、可以提前执行的美式期权、停业之后又重新开业的多阶段期权、事实上不存在最后到期日的期权等复杂情况。二叉树模型可以扩展为三叉树、四叉树模型等，以适应项目存在的多种选择。通常，在BS模型束手无策的复杂情况下，二叉树模型往往能解决问题。

一、扩张期权

点击查看代码

公司的扩张期权包括许多种具体类型÷例如，采矿公司投资于采矿权以获得开发或者不开发的选择权，尽管目前它还不值得开采，但是，产品价格升高后它却可以大量盈利；房屋开发商要投资于土地，经常是建立土地的储备，以后根据市场状况决定新项目的规模；医药公司要控制药品专利，不一定马上投产，而是根据市场需求推出新药。再如，制造业小规模推出新产品，抢先占领市场，以后视市场的反应再决定扩充规模。如果它们今天不投资，就会失去未来扩张的选择权。

【例6-17】A公司是一个颇具实力的智能终端设备制造商。公司管理层估计智能穿戴设备可能有巨大发展，计划引进新型生产技术。
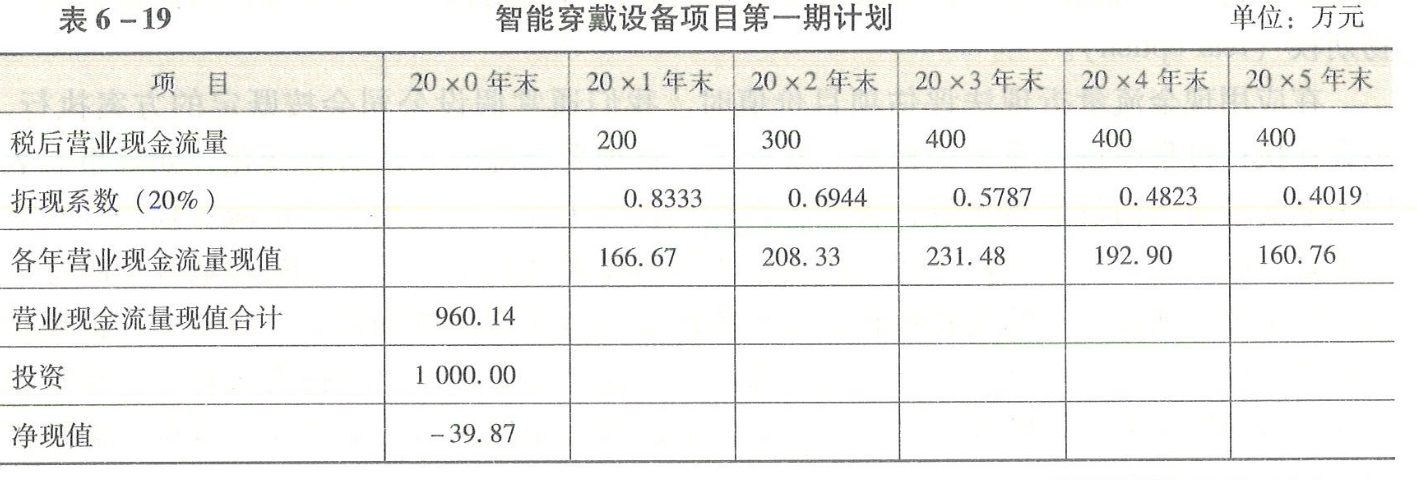
考虑到市场的成长需要一定时间，该项目分两期进行。第一期项目的规模较小，目的是迅速占领市场并减少风险，大约需要投资1000万元；20x1年建成并投产，预期税后营业现金流量如表6-19所示。第二期20x4年建成并投产，生产能力为第一期的2倍，需要投资2000万元，预期税后营业现金流量如表6-20所示。由于该项目风险较大，投资的必要报酬率按20%计算，该项目第一期的净现值为-39.87万元，第二期的净銆ẩ现值为-118.09万元。
表6-19智能穿戴设备项目第一期计划

微信截图_20240521082626.png
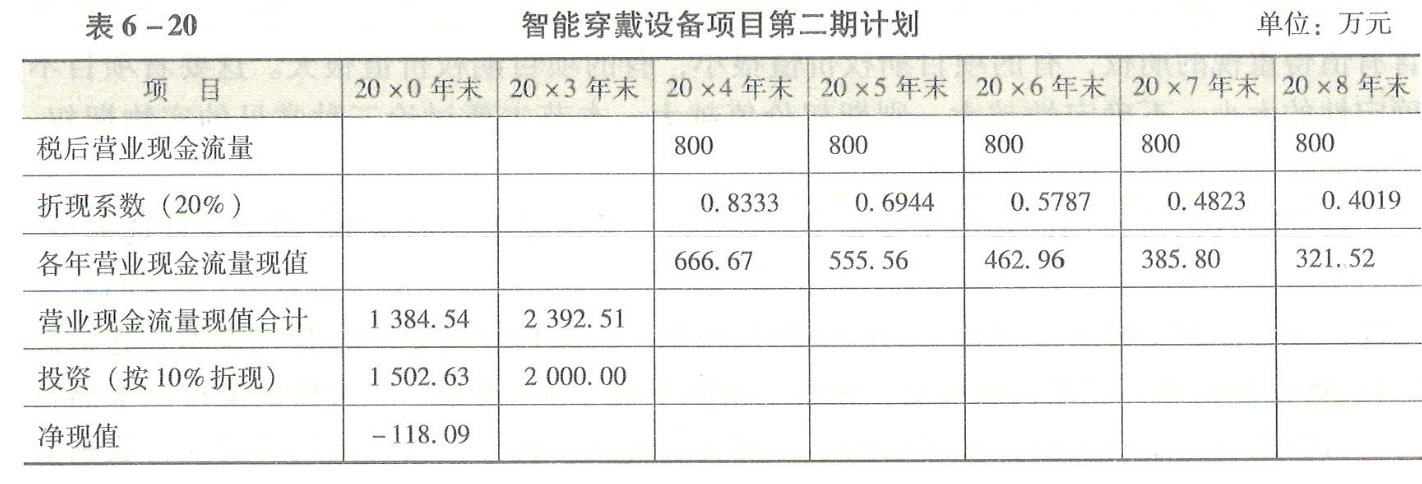
表6-20智能穿戴设备项目第二期计划

微信截图_20240521082637.png
这两个方案采用传统的现金流量折现法分析(即不考虑期权)，均没有达到公司投资必要报酬率。计算净现值时，使用的税后营业现金流量是期望值，实际现金流量可能比期望值高或者低。公司可以在第一期项目投产后，根据市场的发展状况再决定是否上马第二期项目。因此，应当考虑扩张期权的影响，

计算扩张期权价值的有关数据如下：

(1)假设第二期项目的决策必须在20x3年底前决定，即这是一项到期时间为3年的期权。
(2)第二期项目的投资额为2000万元，折算到零时点使用10%作折现率，是因为它是确定的现金流量，在20x1~20x3年中并未投入风险项目。该投资额折现到20x0年底为1502.63万元。它是期权执行价格的现值。
(3)预计未来营业现金流量折现到20x3年底为2392.49万元，折现到20x0年底为1384.54万元。这是期权标的资产的当前价格。
(4)如果营业现金流量现值合计超过投资，就选择执行(实施第二期项目计划)；如果投资超过营业现金流量现值合计，就选择放弃。因此，这是一个看涨期权问题。
(5)智能终端行业风险很大，未来现金流量不确定，可比公司的股票价格标准差头35%，可以作为项目现金流量的标准差。
(6)无风险报酬率为10%。扩张期权与典型的股票期权类似，可以使用BS模型，其计算结果如下：

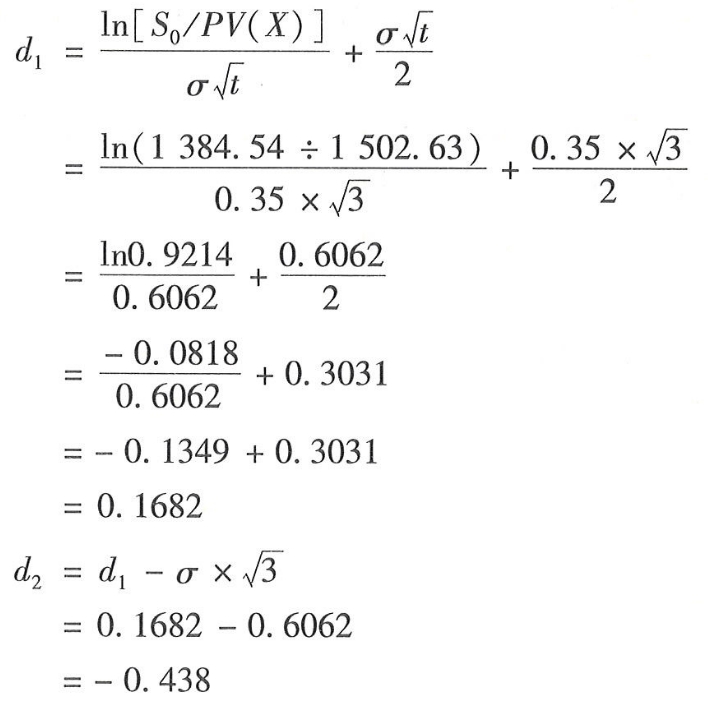
微信截图_20240521082707.png
根据内插法，求得：

微信截图_20240521082717.png
第一期项目不考虑期权的价值是-39.87万元，它可以视为取得第二期开发选择权的成本。投资第一期项目使得公司有了是否开发第二期项目的扩张期权，该扩张期权的价值是287.71万元。考虑期权的第一期项目净现值为247.84万元(287.71-39.87)，因此，投资第一期项目是有利的。

二、延迟期权

从时间选择来看，任何投资项目都具有期权的性质。

如果一个项目在时间上不能延迟，只能立即投资或者永远放弃，那么，它就是马上到期的看涨期权。项目的投资成本是期权执行价格，项目的未来营业现金流量的现值是期权标的资产的现行价格。如果该现值大于投资成本，项目的净现值就是看涨期权的收益。如果该现值小于投资成本，看涨期权不被执行，公司放弃该项投资。
如果一个项目在时间上可以延迟，那么，它就是未到期的看涨期权。项目具有正的净现值，并不意味着立即开始(执行)总是最佳的，也许等一等更好。对于前景不明朗的项目，大多值得观望，看一看未来是更好还是更差，再决定是否投资。

【例6-18】B公司拟投产一个新产品，预计投资需要1050万元，每年营业现金流量为100万元(税后、可持续)，项目的资本成本为10%(无风险报酬率为5%，风险溢价为5%)。
项目价值=永续现金流量÷折现率=100÷10%=1000(万元)
项目的预期净现值=不含期权的项目净现值=项目价值-投资成本=1000-1050=-50(万元)
每年的现金流量100万元是期望值，并不是确定的现金流量。假设一年后可以判断出市场对产品的需求÷如果新产品受顾客欢迎，预计每年营业现金流量为120万元；如果不受欢迎，预计每年营业现金流量为80万元。由于未来营业现金流量具有不确定性，应当考虑期权的影响。
延迟期权大多使用二叉树模型。虽然例题假设一年后可以判断需求情况，实际上也可能需要继续等待。具有时间选择灵活性的项目，本身并没有特定的期权执行时间，并不符合典型股票期权的特征。

利用二叉树方法进行分析的主要步骤如下：

(1)构造现金流量和项目价值二叉树。
项目价值=永续现金流量÷折现率
上行项目价值=120÷10%=1200(万元)
下行项目价值=80÷10%=800(万元)
(2)构造净现值二叉树。
上行净现值=1200-1050=150(万元)
下行净现值=800-1050=-250(万元)
(3)根据风险中性原理计算上行概率。
报酬率=(本年现金流量+期末项目价值)÷期初项目价值-1
上行报酬率=(120+1200)÷1000-1=32%
下行报酬率=(80+800)÷1000-1=-12%
无风险报酬率=上行概率x上行报酬率+下行概率x下行报酬率
5%=上行概率x32%+(1-上行概率)x(-12%)
上行概率=0.3864
下行概率=1-0.3864=0.6136
(4)计算含有期权的项目净现值。
含有期权的项目净现值(延迟投资时点)=0.3864x150+0.6136x0=57.96(万元)
含有期权的项目净现值(现在时点)=57.96÷1.05=55.2(万元)
期权的价值=55.2-(-50)=105.2(万元)
以上计算结果，用二叉树表示如表6-21所示，
表6-21投资成本为1050万元的期权价值

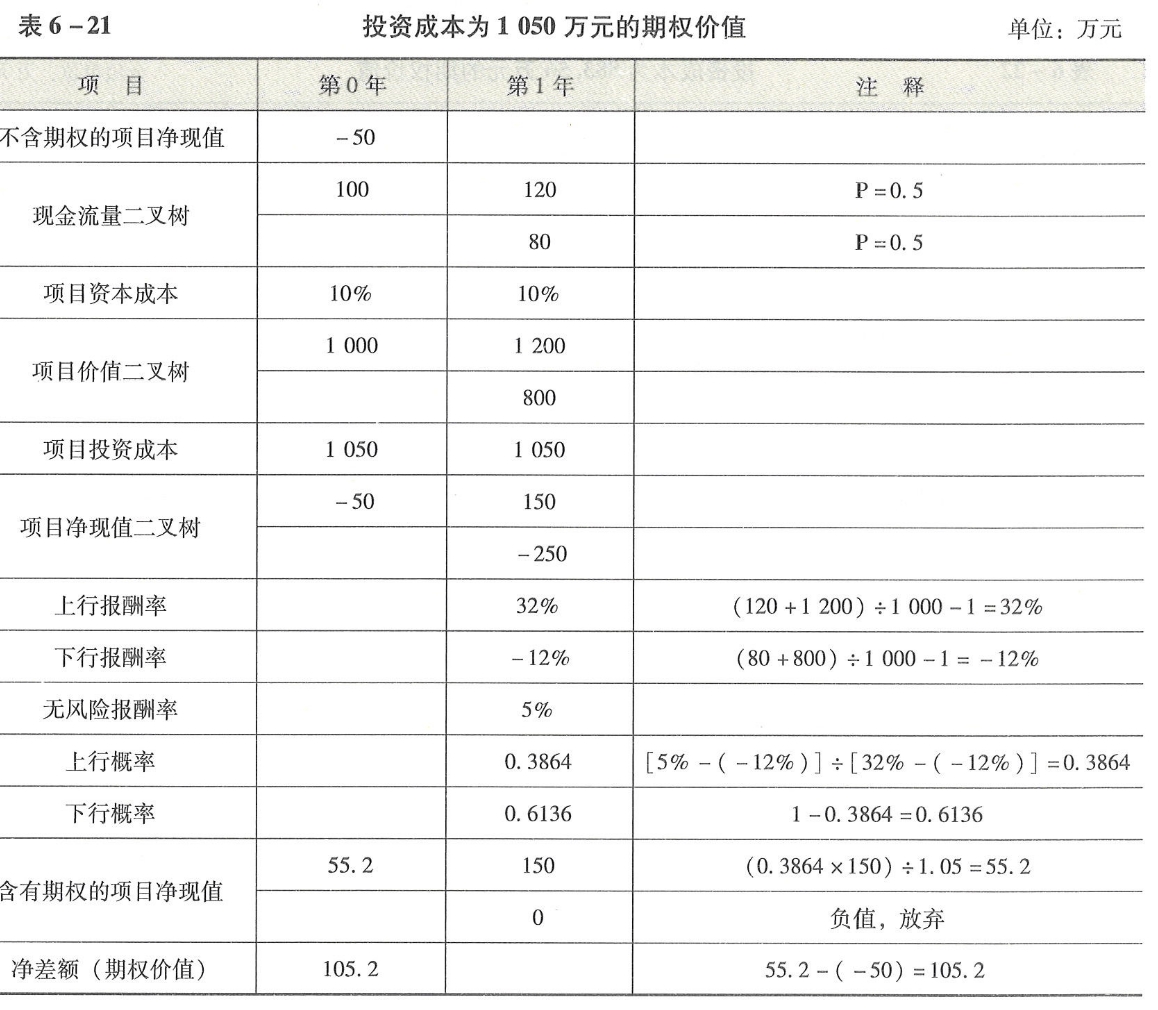
微信截图_20240521082816.png
(5)判断是否应延迟投资。
如果立即投资该项目，其净现值为负值，不是有吸引力的项目；如果等待，考虑期权后的项目净现值为正值，是个有价值的投资项目，因此应当等待。此时的净现值的增加是由于考虑期权引起的，实际上就是该期权的价值。

等待不一定总是有利，延迟期权的价值受投资成本、未来现金流量的不确定性、资本成本和无风险报酬率等多种因素的影响。
假设其他因素不变，如果投资成本降低，则项目的预期净现值增加，含有期权的项目净现值也增加，但是后者增加较慢，并使两者的净差额(期权价值)逐渐缩小。

就本例题而言，

两者的增量之比为÷上行概率÷(1+无风险报酬率)=0.3864÷1.05=0.3680。
该项目的投资成本由1050万元降低为883.56万元时，预期净现值由-50万元增加到116.44万元，增加166.44万元。
含有期权的项目净现值从55.2万元增加到116.44万元(见表6-22)，只增加61.24万元。
两者增量的差额为105.2万元，即期权价值完全消失。在这种情况下，期权价值为零，等待已经没有意义。因此，如果投资成本低于883.56万元，立即执行项目更有利，
表6-22投资成本为883.56万元的期权价值

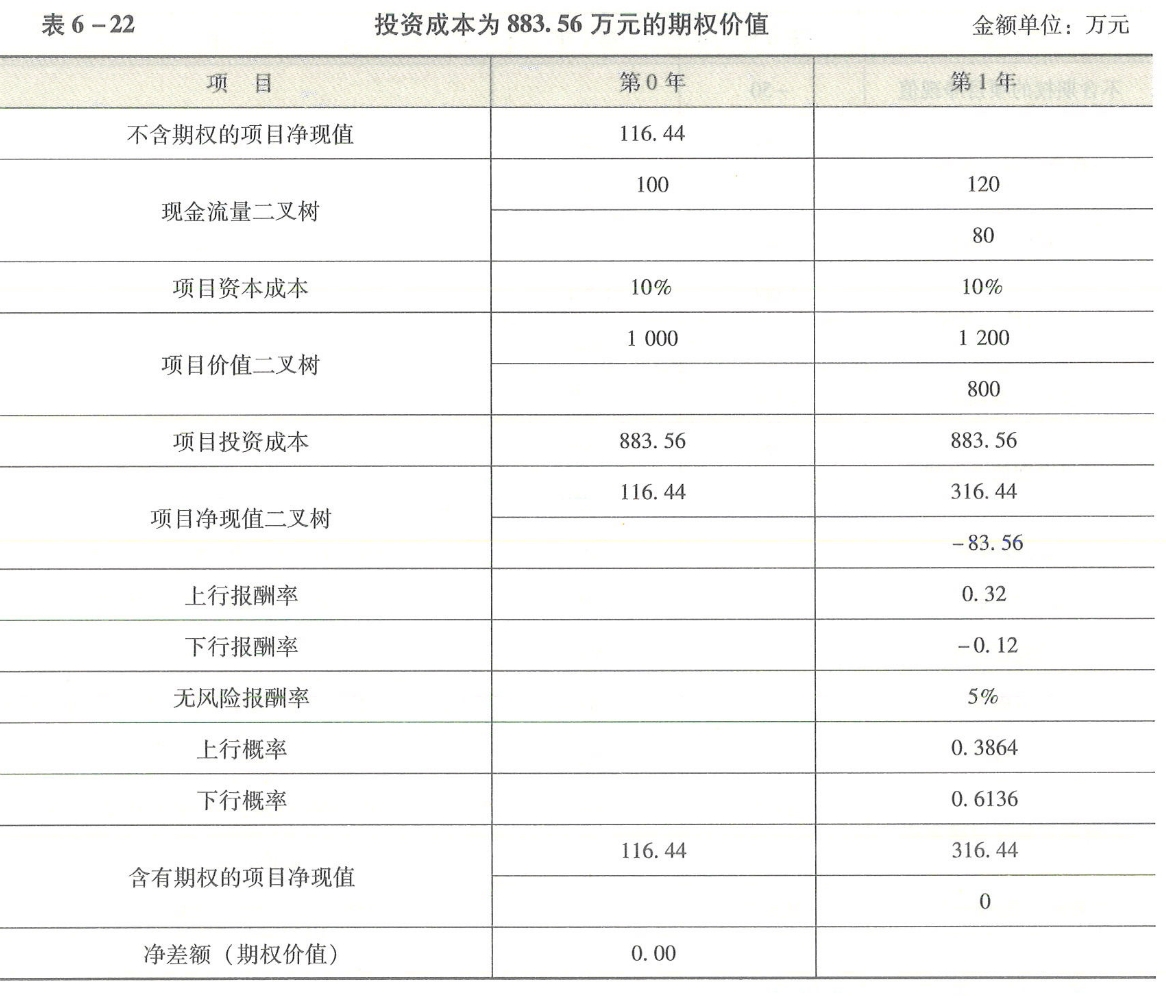
微信截图_20240521083131.png

计算投资成本临界值的方法如下：

项目的预期净现值=不含期权的项目净现值=项目价值-投资成本=1000-投资成本
含有期权的项目净现值=[上行概率x(上行项目价值-投资成本)+下行概率x(下行项目价值一投资成本)]÷(1+无风险报酬率)
投资成本大于或等于下行项目价值时放弃项目，则：
含有期权的项目净现值=上行概率x(上行项目价值-投资成本)÷(1+无风险报酬率)
=「0.3864x(1200-投资成本)]÷1.05
令项目的预期净现值与含有期权的项目净现值相等，则：
1000-投资成本=[0.3864x(1200-投资成本)]÷1.05
投资成本=883.56万元

三、放弃期权

点击查看代码

在评估项目时，我们通常选定一个项目的寿命周期，并假设项目会进行到寿命周期结束。这种假设不一定符合实际。如果项目执行一段时间后，实际产生的现金流量远低于预期，投资者就会考虑提前放弃该项目，而不会坚持到底。另外，经济寿命周期也很难预计。项目开始时，往往不知道何时结束。有的项目，一开始就不顺利，产品不受市场欢迎，一两年就被迫放弃了。有的项目，越来越受市场欢迎，产品不断升级换代，或者扩大成为一系列产品，几十年长盛不衰。
一个项目，只要继续经营价值大于资产的清算价值，它就会继续下去。反之，如果清算价值大于继续经营价值，就应当终止。这里的清算价值，不仅指残值的变现收入也包括有关资产的重组和价值的重新发掘。
在评估项目时，就应当事先考虑中间放弃的可能性和它的价值。这样，可以获得项目更全面的信息，减少决策错误。放弃期权是一项看跌期权，其标的资产价值是项目的继续经营价值，而执行价格是项目的清算价值。
一个项日何时应当放弃，在项目启动时并不明确。缺少明确到期期限的实物期权不便于使用BS模型。虽然在项目分析时可以假设一个项目有效期，但是实际上多数项目在启动时并不确知其寿命。有的项目投产后很快碰壁，只有一两年的现金流量；有的项目很成功，不断改进的产品使该项目可以持续几十年。在评估放弃期权时，需要预测很长时间的现金流量，逐一观察历年放弃或不放弃的项目价值，才能知道放弃期权的价值。

【例6-19】C公司拟开发一个玉石矿，预计需要投资1200万元；矿山的产量每年约29吨，假设该矿藏只有5年的开采量；该种玉石的价格目前为每吨10万元，预计每年上涨11%，但是很不稳定，其标准差为35%，因此，销售收入应当采用含有风险的必要报酬率10%作为折现率。
营业的固定成本每年100万元。为简便起见，忽略其他成本和税收问题。由于固定成本比较稳定，可以使用无风险报酬率5%作为折现率。
1~5年后矿山的残值分别为530万元、500万元、400万元、300万元和200万元。

放弃期权的分析程序如下：

(1)计算项目的净现值。
实物期权分析的第一步是计算标的资产的价值，也就是不含期权的项目净现值。用现金流量折现法计算的净现值为-19万元(表6-23)。
表6-23项目的净现值
微信截图_20240521083237.png
如果不考虑期权，项目净现值为负值，是个不可取的项目。
(2)构造二叉树。
微信截图_20240521083254.png
以下各年的二叉树以此类推，如表6-24所示。
表6-24放弃期权的二叉树
微信截图_20240521083306.png
微信截图_20240521083319.png
③构造营业现金流量二叉树。由于固定成本为每年100万元，销售收入二叉树各节点减去100万元，可以得出营业现金流量二叉树。
④确定上行概率和下行概率。
期望收益率=上行百分比x上行概率+(-下行百分比)x(1-上行概率)
5%=(1.419068-1)x上行概率+(0.704688-1)x(1-上行概率)
上行概率=0.483373
下行概率=1-上行概率=1-0.483373=0.516627
⑤确定未修正项目价值。首先，确定第5年各节点未修正项目价值。由于项目在第5年年末终止，无论哪一条路径，最终的清算价值均为200万元。然后，确定第4年年末的项目价值，顺序为先上后下。最上边的节点价值取决于第5年的上行现金流量和下行现金流量。它们又都包括第5年的营业现金流量和第5年年末的残值。
第4年末项目价值=[px(第5年上行营业现金流量+第5年期末价值)+(1-p)x(第5年下行营业现金流量+第5年期末价值)]÷(1+r)
=[0.483373x(1568.83+200)+0.516627x(728.72+200)]÷(1+5%)
=1271.25(万元)
其他各节点以此类推。
⑥确定修正项目价值。各个路径第5年的期末价值均为200万元，不必修正，填入“修正项目价值”二叉树相应节点。
第4年各节点由上而下进行，检查项目价值是否低于同期清算价值(300万元)。该年第4个节点数额为239.25万元，低于清算价值300万元，清算比继续经营更有利，因此该项目应放弃，将清算价值填入“修正项目价值”二叉树相应节点。此时相应的销售收入为144.01万元。需要修正的还有第4年最下方的节点166.75万元，用清算价值300万元取代；第3年最下方的节点198.43万元，用清算价值400万元取代；第2年最下方的节点332.47万元，用清算价值500万元取代。
完成以上4个节点的修正后，重新计算各节点的项目价值。计算的顺序仍然是从后向前，从上到下，依次进行，并将结果填入相应的位置。最后，得出0时点的项目价值为122嗆鲎肝宅ヴ幻万醵元。

(3)确定最佳放弃策略。

点击查看代码

由于项目考虑期权的现值为1221万元，投资为1200万元，所以：
含有期权的项目净现值=1221-1200=21(万元)
不含期权的项目净现值=-19万元
期权的价值=含有期权的项目净现值-不含期权的项目净现值=21-(-19)
=40(万元)
因此，公司应当进行该项目。但是，如果价格下行使得销售收入等于或低于144.01万元时(即清算价值大于继续经营价值)应放弃该项目，进行清算。
那么，公司是否应当立即投资该项目呢?不一定。还需进行延迟期权的分析才知道。