数据结构面试题及答案讲解+二叉树专题（下）+腾讯+字节跳动常考题

@

目录

• 本节目标
  • 1、求二叉树的镜像（腾讯2020年面试原题）
  • 2、二叉树的层序遍历（字节跳动2018年面试原题）
  • 3、二叉树的前序非递归遍历、中序非递归遍历、后序非递归遍历（字节跳动2020年面试原题）
• 1、求二叉树的镜像。
  • 解题思路：
  • 代码实现：
• 2、二叉树的层序遍历
  • 高频考察的大厂云图：
  • 解题思路：
  • 代码实现：
• 3、二叉树的前序非递归遍历、中序非递归遍历、后序非递归遍历
  • 高频考察的大厂云图：
  • 解题思路：
  • 问题分析：
  • 代码实现：
• 视频讲解

本节目标

• 1、求二叉树的镜像（腾讯2020年面试原题）

• 2、二叉树的层序遍历（字节跳动2018年面试原题）

• 3、二叉树的前序非递归遍历、中序非递归遍历、后序非递归遍历（字节跳动2020年面试原题）

1、求二叉树的镜像。

OJ链接：https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof/

解题思路：

镜像其实就是镜子中的成像，也就是跟当前树镜子中对称的树，也就是将每个树的左右孩子交换，如下图。

代码实现：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root == NULL)
            return NULL;
        
        swap(root->left, root->right);
        mirrorTree(root->left);
        mirrorTree(root->right);
        
        return root;
    }
};

2、二叉树的层序遍历

OJ链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

高频考察的大厂云图：

解题思路：

BFS(广度优先遍历)遍历，DFS(深度优先遍历)遍历，是树型结构的两种遍历方式。本题既可以使用BFS，也可以使用DFS，不过一般情况下，BFS做起来容易理解一些，所以我们这个题就直接队列BFS的方式完成就可以，下一个题我们会使用DFS的方式看来完成。

思路：本题是二叉树层序遍历的变形，因为还要要求分层打印。

1. 本题我们使用队列的FIFO(先进先出)的性质，根先进队列。
2. 根出来时代入下一层的子节点，子节点出来时再代入下一层子节点。
3. 不断重复直到队列为空。
4. 总结一下：上一层出时带入下一层进队列，那么节点在队列中是先进先出的，所以整个树是一层一层遍历的

思路：本题是二叉树层序遍历的变形，因为还要要求分层打印。

1. 要实现分层遍历，我们可以巧妙的控制每层的节点个数来完成。
2. 最开始我们将根入到队列中，那么这时队列的数据个数就是第一层的数据个数。
3. 遍历时用一个循环控制一层一层出，如果第一层出完了，第二层的节点就都被代入队列中了。
4. 以此类推，第N层出完了，队列中就是第N+1层的节点，这样我们就把数据一层层分开了。

代码实现：

/*
思路：二叉树层序遍历的变形
1. 如果是空树直接返回
2. 层序遍历需要用到队列，定义一个队列，里面放置节点的地址，将根节点如队列
3. 队列非空时，循环进行一下操作：
    a. 队列中当前元素都是在同一层的，依次取出遍历，保存到同一个vector中
        取到一个节点时候：
           >> 保存该节点
           >> 如果该节点左子树存在，将该左子树入队列
           >> 如果该节点右子树存在，将该节点右子树入队列
           >> 将当前已遍历节点从队列中拿出来
     b. 本层节点遍历结束后，保存到返回的vector中，此时下一层节点已经全部入队列
*/
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) 
    {
        // 如果是空树直接返回
        vector<vector<int>> ret;
        if(nullptr == root)
            return ret;
        
        queue<TreeNode*> q;
        q.push(root);   // 已经将第一层节点放到队列中
        
        while(!q.empty())
        {
            // 一次性将一层的所有节点全部遍历完
            vector<int> level;
            int levelSize = q.size();
            
            // 该for将本层节点变量完成后，已经将下一层节点保存到队列中
            for(size_t i = 0; i < levelSize; ++i)
            {
                TreeNode* front = q.front();
                level.push_back(front->val);
                
                // 如果该节点有左右子树，分别将左右子树入队列
                if(front->left)
                    q.push(front->left);
                
                if(front->right)
                    q.push(front->right);
                
                q.pop();
            }
            
            ret.push_back(level);
        }
        
        return ret;
    }
};

3、二叉树的前序非递归遍历、中序非递归遍历、后序非递归遍历

前序遍历OJ链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

中序遍历OJ链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

后序遍历OJ链接：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/

高频考察的大厂云图：

解题思路：

1. 本题本质就是二叉树的DFS遍历。

2. 下图分别展示了什么是前序、中序、后序遍历，我们简单复习一下。

问题分析：

1. 这里要使用递归实现前中后序遍历非常简单，但是面试时的要求基本都要求是非递归遍历。
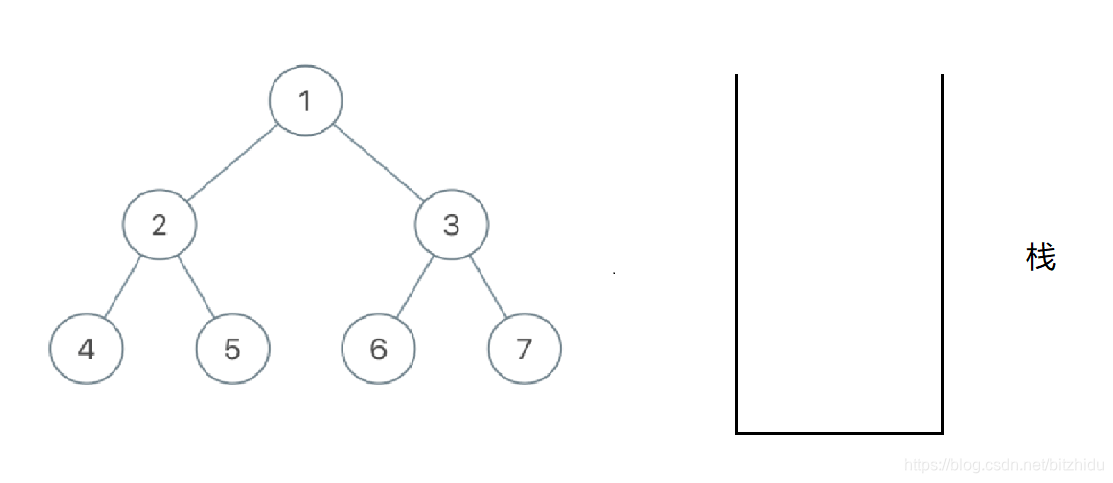
2. 这三个题本质都是类似的，我们非递归要借助栈来完成
3. 我们把一棵树分成两个部分来看待，左路节点和左路节点的右子树。
4. 右子树使用遍历子树的思想来完成。
5. 本题还是比较复杂和抽象，是个硬菜，更细节的过程我们上课时通过图结合代码讲解。

代码实现：

/*
思路：前序非递归遍历需要借助栈
  1. 如果树为空，直接返回
  2. 如果树非空：从根节点位置开始遍历，但此时根节点不能遍历，因为中序遍历规则：左子树、根节点、右子树
      a. 沿着根节点一直往左走，将所经过路径中的节点依次入栈，并访问。
      b. 取栈顶元素，该元素取到后，其左子树要么为空，要么已经遍历，可以直接遍历该节点，对于该节点，          其左子树已经遍历，该节点也已经遍历，剩余其右子树没有遍历，将其左子树当成一棵新的树开始遍            历，继续a
具体实现：参考代码，学生自己动手画图理解
*/
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(!st.empty() || cur)
        {
            // 每次循环表示要开始访问一颗树了，先将一颗数的左路节点都入栈并访问节点
            // 剩余左路节点的右子树还没访问
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }

            // 取栈中的节点依次访问左路节点的右子树
            TreeNode* top = st.top();
            st.pop();
            cur = top->right;
        }

        return v;
    }
};

/*
思路：中序非递归遍历需要借助栈
 1. 空树，直接返回
 2. 如果树非空：从根节点位置开始遍历，但此时根节点不能遍历，因为中序遍历规则：左子树、根节点、右子树
      a. 沿着根节点一直往左走，将所经过路径中的节点依次入栈
      b. 取栈顶元素，该元素取到后，其左子树要么为空，要么已经遍历，可以直接遍历该节点，对于该节点，          其左子树已经遍历，该节点也已经遍历，剩余其右子树没有遍历，将其左子树当成一棵新的树开始遍            历，继续a
具体实现：参考代码，学生自己动手画图理解
*/
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        
        // 空树，直接返回
        vector<int> vRet;
        if(nullptr == root)
            return vRet;
        
        TreeNode* pCur = root;
        stack<TreeNode*> s;
        while(pCur || !s.empty())
        {
            // 找以pCur为根的二叉树最左侧的节点，并将所经路径中的节点入栈
            while(pCur)
            {
                s.push(pCur);
                pCur = pCur->left;
            }

            pCur = s.top();
            
            // pCur左子树为空，相当于左子树已经访问过了，可以直接访问以pCur为根的二叉树的根节点
            vRet.push_back(pCur->val);
            s.pop();
            
            // 以pCur为根的二叉树的左子树已经遍历完，根节点已经遍历，
            // 将pCur的右子树当成一棵二叉树来遍历
            pCur = pCur->right;
        }

        return vRet;
    }
};

/*
思路：后序非递归遍历需要借助栈
 1. 空树，直接返回
 2. 如果树非空：从根节点位置开始遍历，但此时根节点不能遍历，因为后序遍历规则：左子树、右子树、根节点
      a. 沿着根节点一直往左走，将所经过路径中的节点依次入栈
      b. 取栈顶元素，该元素取到后，其左子树要么为空，要么已经遍历，
         但是此时该节点不能遍历，除非其右子树不存在或者其右子树已经遍历，才可以遍历该节点
         如果该节点右子树没有遍历，将其右子树作为一棵新的二叉树遍历，继续a
具体实现：参考代码，学生自己动手画图理解
*/
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        // 空树直接返回
        vector<int> vRet;
        if(nullptr == root)
            return vRet;
        
        TreeNode* pCur = root;
        TreeNode* pPrev = nullptr;
        stack<TreeNode*> s;
        while(pCur || !s.empty())
        {
            // 找以pCur为根的二叉树最左侧的节点，并将所经路径中的节点入栈
            while(pCur)
            {
                s.push(pCur);
                pCur = pCur->left;
            }

            TreeNode* pTop = s.top();
            
            // pTop左子树已经访问
            // 如果pTop的右子树是空，或者右子树已经访问过了，就可以访问pTop
            if(nullptr == pTop->right || pPrev == pTop->right)
            {
                vRet.push_back(pTop->val);
                s.pop();
                
                // 将刚刚访问过的节点标记起来
                pPrev = pTop;
            }
            else
            {
                // 如果右子树没有访问，将右子树当成一棵新的二叉树访问
                pCur = pTop->right;
            }
        }

        return vRet;
    }
};

视频讲解

如果看完文章，你还是没有太明白，请看视频讲解：
数据结构面试题及答案讲解+二叉树专题（下）+腾讯+字节跳动常考题

文章还不错，请点赞
想看什么内容，请留言
持续更新有价值的内容~~