Codeforces 1133 F2. Spanning Tree with One Fixed Degree 并查集+生成树
好久没更新博客了,一直懒得动,这次更新一下。
题意大概是:给出一个图,求它的一个一号节点的度数恰好为D的生成树的方案。
一开始随便水了个乱搞贪心,不出意外并没有过。
仔细思考之后,对于这个问题我们可以先不管有一端是1的边,然后在这样的子图中,观察节点联通块的情况。
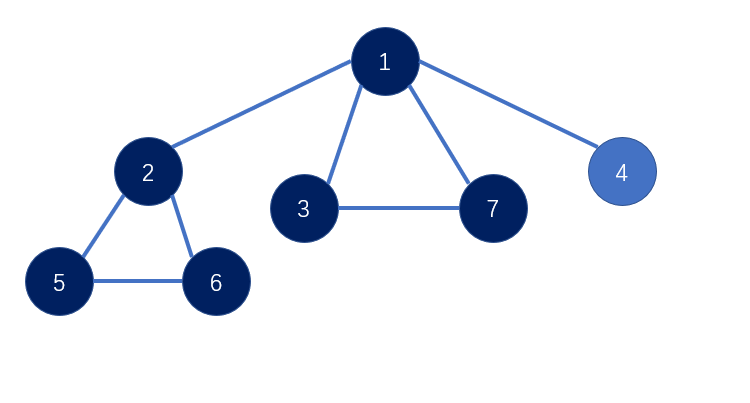
如上图,我们可以认为{2,5,6},{3,7},{4}分别是一个联通块。
为了保证最后生成树的连通性,显然每个联通块最少要连接一条对节点1的边。
这样一来我们就可以自由地连接剩下的边,当然,要符合生成树的性质,用并查集来判断是否能连接这条边。
于是我们用剩下的对1连接的边来使得1的度数符合要求。
然后接下来再用剩下的其他边补全生成树即可。
#include<bits/stdc++.h>
using namespace std;
int i,i0,n,m,D,pre[200005],pre0[200005];
bool vis[200005];
vector<int>v[200005];
vector<pair<int,int>>v0,ans;
int fin(int x){return (pre[x]==x)?x:pre[x]=fin(pre[x]);}
void uni(int x,int y){if(fin(x)!=fin(y))pre[fin(y)]=fin(x);}
int fin0(int x){return (pre0[x]==x)?x:pre0[x]=fin0(pre0[x]);}
void uni0(int x,int y){if(fin0(x)!=fin0(y))pre0[fin0(y)]=fin0(x);}
int main()
{
scanf("%d %d %d",&n,&m,&D);
for(i=1;i<=n;i++)pre[i]=pre0[i]=i;
for(i=1;i<=m;i++)
{
int x,y;
scanf("%d %d",&x,&y);
if(x>y)swap(x,y);
if(x!=1)uni(x,y),v0.push_back({x,y});
else vis[y]=1;
}
for(i=1;i<=n;i++)if(vis[i])v[fin(i)].push_back(i);
for(i=2;i<=n;i++)
{
if(fin(i)==i)
{
D--;
uni0(1,v[i][v[i].size()-1]);
ans.push_back({1,v[i][v[i].size()-1]});
v[i].pop_back();
}
}
for(i=2;i<=n;i++)
{
if(fin(i)==i)
{
while(D&&v[i].size())
{
D--;
uni0(1,v[i][v[i].size()-1]);
ans.push_back({1,v[i][v[i].size()-1]});
v[i].pop_back();
}
}
}
for(auto i:v0)if(fin0(i.first)!=fin0(i.second))uni0(i.first,i.second),ans.push_back({i.first,i.second});;
bool f=1;
for(i=2;i<=n;i++)if(fin0(i)!=fin0(1))f=0;
if(f&&!D)
{
printf("YES\n");
for(auto i:ans)printf("%d %d\n",i.first,i.second);
}
else printf("NO\n");
return 0;
}

