浮点运算与boost.multiprecision

在C++中，float占4个字节，double占8个字节，均采用 IEEE 754 浮点标准；内部都是以二进制为基础，表述实数，有些实数可以被精确表述，比如0.2，但有些不行，比如0.3。针对这一点，前不久有篇专门的文章介绍这个：浮点运算为什么不准？有人为0.30000000000000004建了个网站

IEEE 754浮点标准

IEEE标准包含一组实数的二进制表示。一个浮点数字包含三个部分：符号(+或者-)、尾数(包含一串有效数位)和一个指数，这些部分都在一个计算机字里。常用的浮点数精度有：单精度(C++内的float类型)、双精度(C++内的double类型)，分配的数位分别是32、64。这些数位被分成如下不同的部分：

精度	符号	指数	尾数
float	1	8	23
double	1	11	52

以双精度浮点数为例，每个浮点数字被分配了8字节，或者64位，来存储对应的三个部分。每个字都具有如下的形式

\[se_1e_2...e_{11}b_1b_2...b_{52} \]

其中第一位保存了符号位，后面11位用于保存指数，再后面小数点后的52位保存尾数。符号位是0表示正数，1表示负数。11位的指数表示的正二进制整数，这些正数通过往指数上叠加 \(2^{10}-1=1023\) 得到，指数范围在-1022和1023之间。e1...e11覆盖了从1到2046之间对应的指数，由于特殊目的，这里没有使用0和2047。

机器精度

机器精度对应的数字，是1和比1大的最小浮点数之间的距离，对于IEEE双精度浮点表示，该值为 \(2^{-52}\)，对应 float.h 文件内宏 DBL_EPSILON 的值。

最小的可表达双精度数字

\(2^{-52}*2^{-1022}\) 是最小的可表达双精度数字。最小可表达数字和机器精度之间的差别是在于，许多在机器精度以下的数字都是机器可表达的数字，尽管将这些数字加到1上可能没有什么影响，另一方面，在最小可表达数字以下的双精度数字完全不能被表示。

boost multiprecision

为了能够表述更高精度的浮点数，就得向库方向查找了。gmp, mpfr 可以表述无限精度，但编译只能gcc吧，boost在1.56版时开始提供 boost.multiprecision 用于支持更高精度数值表述，许可证较其他库宽松，但在计算效率等方向要逊于gmp, mpfr。

比如采用 bbp 公式(可参考The BBP Algorithm for Pi)计算 pi 的精确结果，代码如下：

// Author: bitbybit3d@163.com

#include <iostream>
#include <iomanip>
#include <boost/math/constants/constants.hpp>
#include <boost/multiprecision/cpp_bin_float.hpp>

// 通过 BBP 公式计算 PI
template <class Type>
Type calc_pi_bbp(int n)
{
    Type pi = 0;

    std::streamsize prevsize = std::cout.precision(50);
    for (int k = 0; k < n; ++k)
    {
        Type it = static_cast<Type>(1) / pow(16, k)
            * (static_cast<Type>(4) / (8 * k + 1) 
                - static_cast<Type>(2) / (8 * k + 4)
                - static_cast<Type>(1) / (8 * k + 5)
                - static_cast<Type>(1) / (8 * k + 6));
        pi += it;
        std::cout << std::left << std::setw(8) << k << pi << std::endl;
    }
    std::cout.precision(prevsize);
    return pi;
}

int main(int argc, char* argv[])
{
    std::cout << "Use double: " << std::endl;
    calc_pi_bbp<double>(20);
    std::cout << std::endl;

    std::cout << "Use boost multiprecision: " << std::endl;
    calc_pi_bbp<boost::multiprecision::cpp_bin_float_100>(30);
    return 0;
}

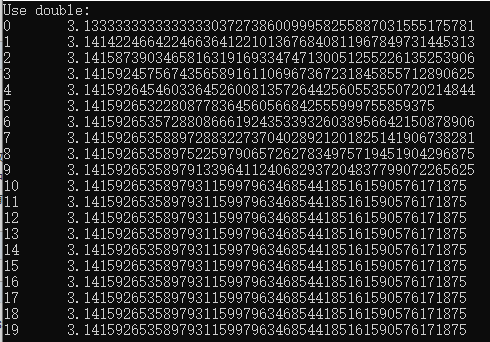
以double值计算20次结果如下：

再以boost.multiprecision计算30次结果如下：

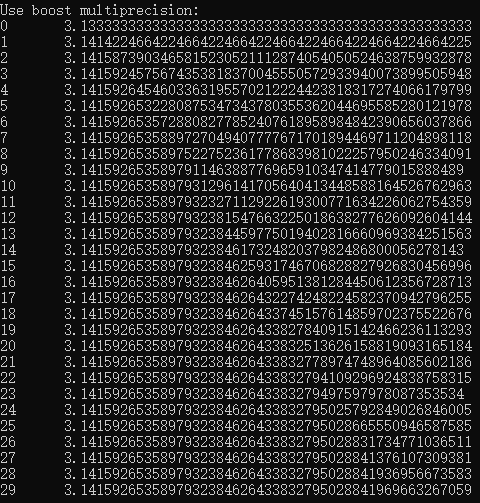
明显使用double计算时，第10次之后就每没有什么变化了(小于2.2204460492503131e-016 (即DBL_EPSILON)的值与 1.0 相加仍然为1.0)，而boost.multiprecision还一直在变化，并且结果可以与Window操作系统中计算器存储的pi值相同(但小数点之后更多数字，这些准不准确就没比较了)。