机器学习笔记11
聚类
1.1 无监督学习简介 Unsupervised learning introduction
之前学习的监督学习都是在训练集有标签的前提下，找到一个决策边界来区别正类和负类
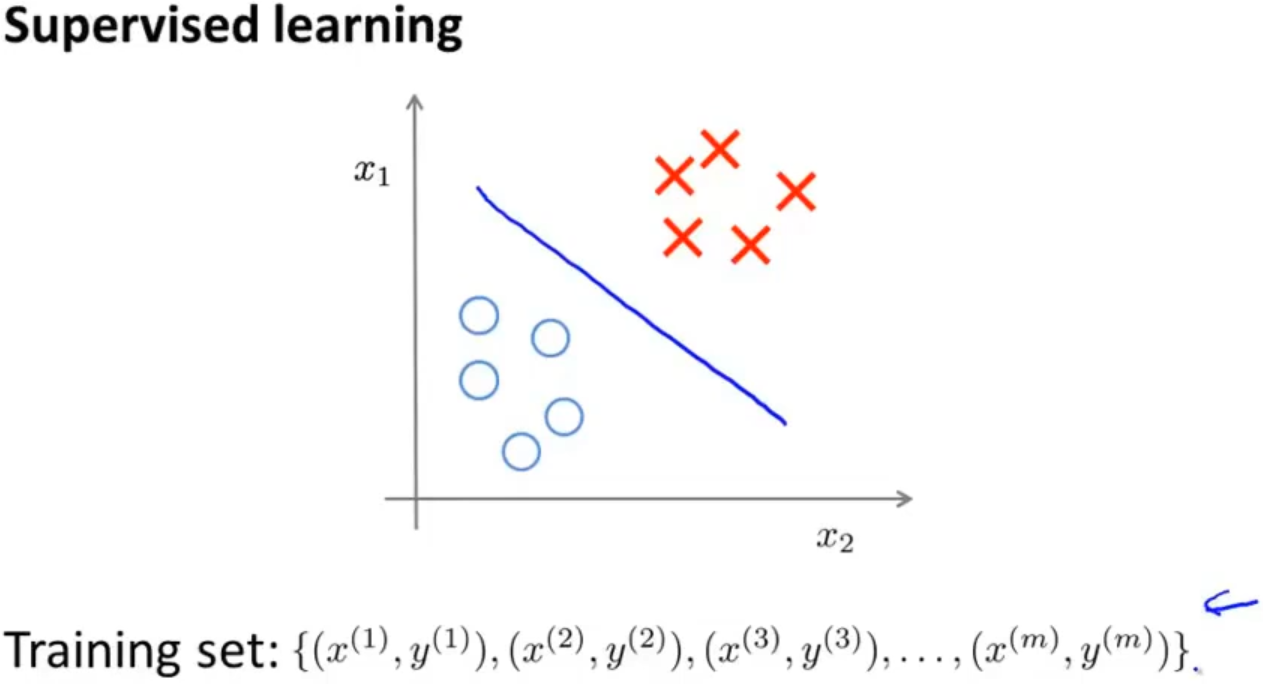
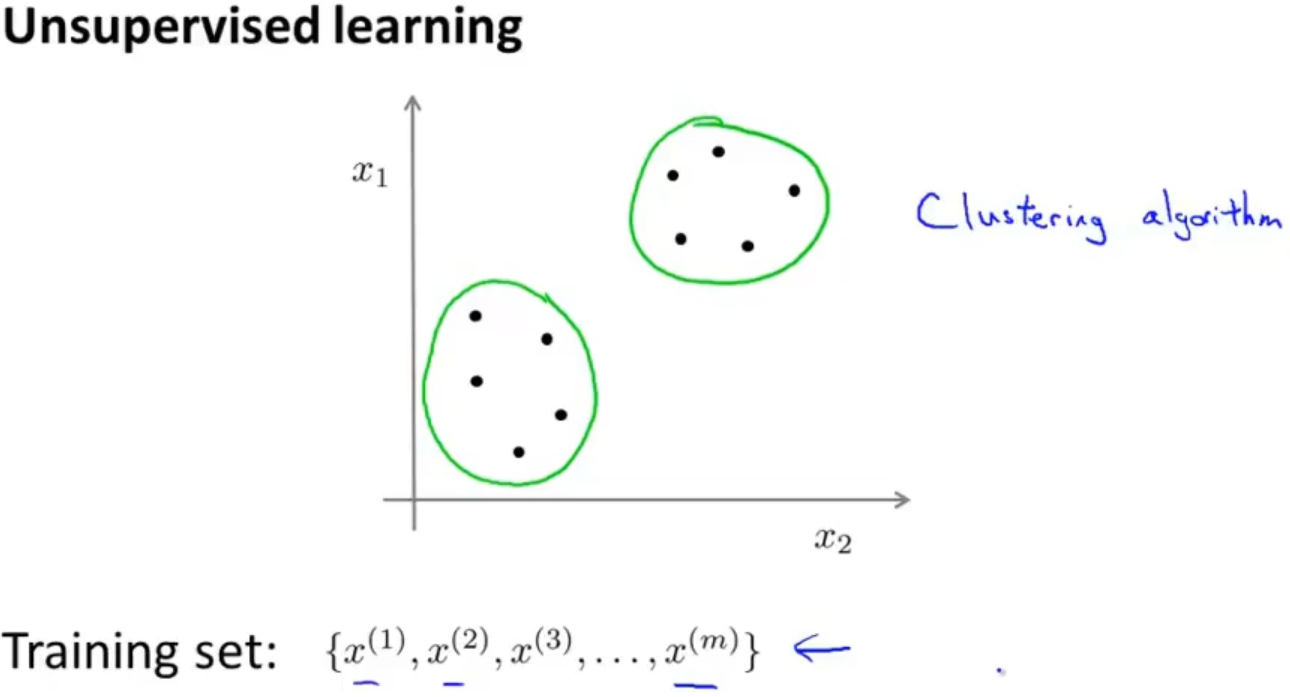
而无监督学习的训练集无标签的，通过算法对数据进行分类
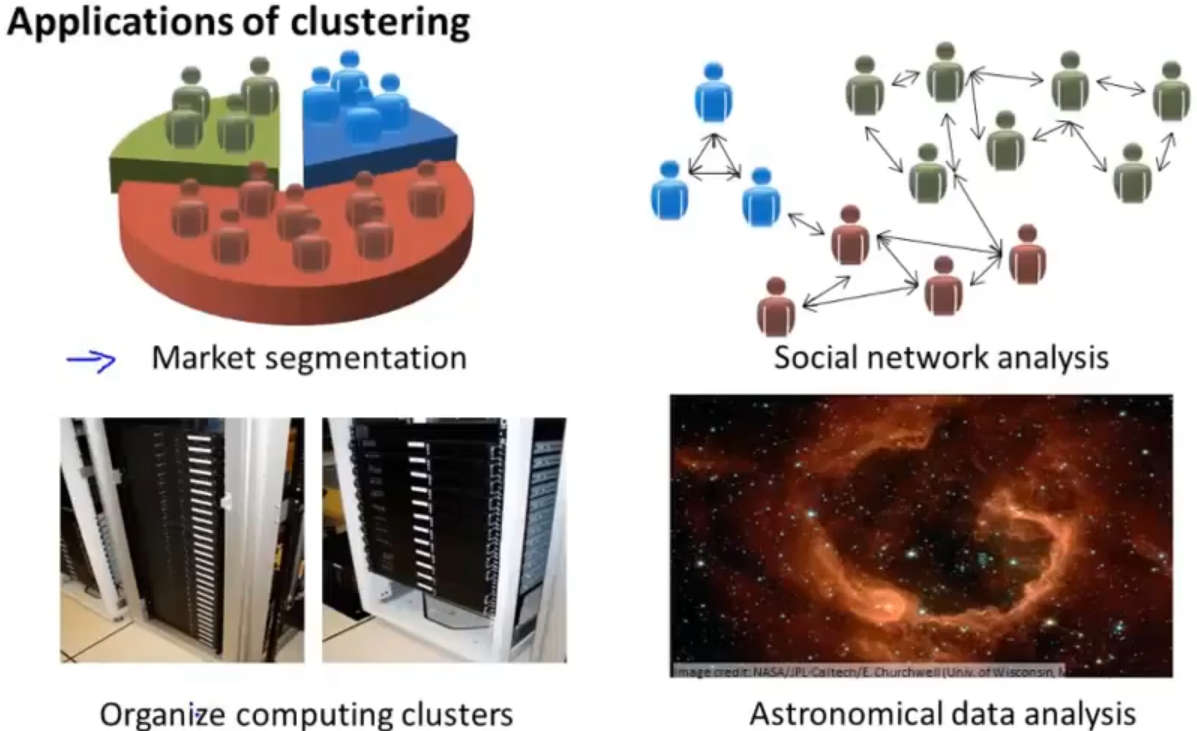
无监督学习的应用：
1.2 K均值算法 K-means algorithm
先来学习第一个无监督算法：聚类算法，在聚类算法中比较经典那肯定是K均值算法了
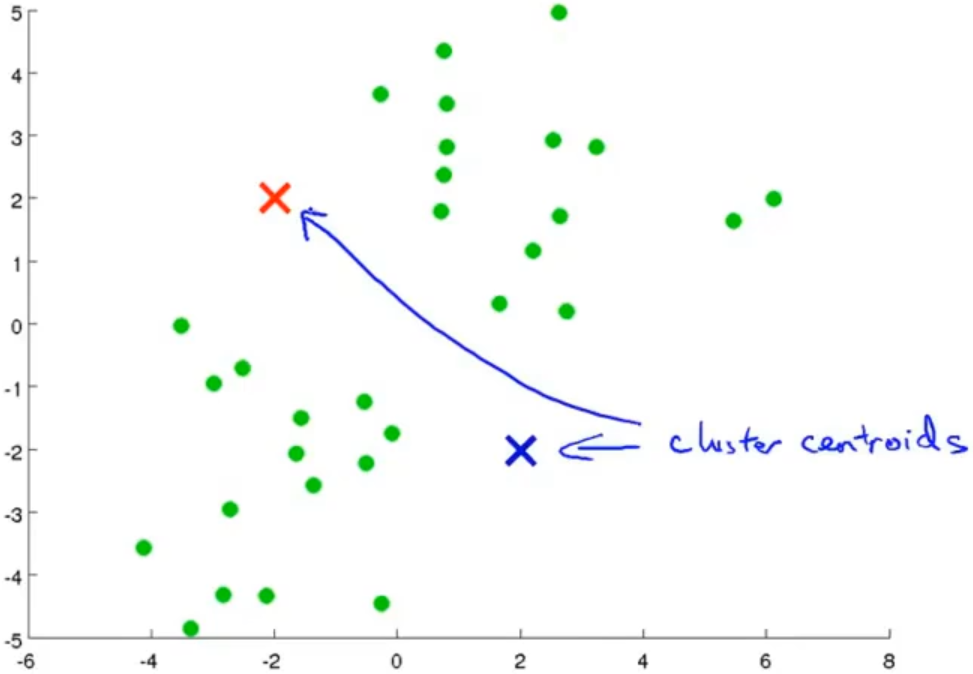
K均值算法其实就是先随机初始化K个聚类中心，通过数据点与聚类中心的距离来更新数据点的类别，最后再对距离中心进行更新，通过不断的迭代，直到所有数据点都不更新了
以下为K均值算法的更新过程：
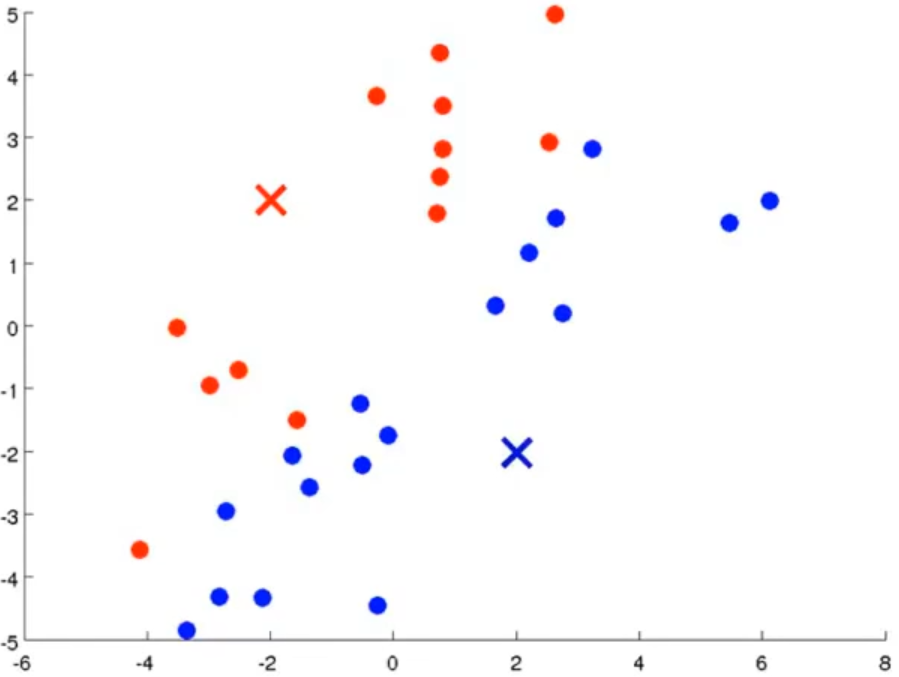
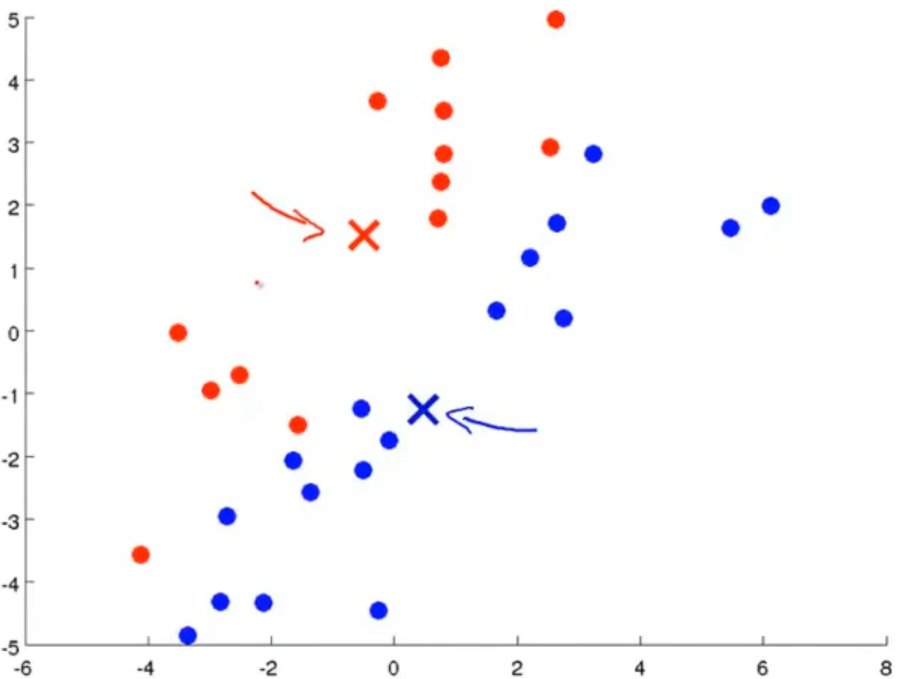
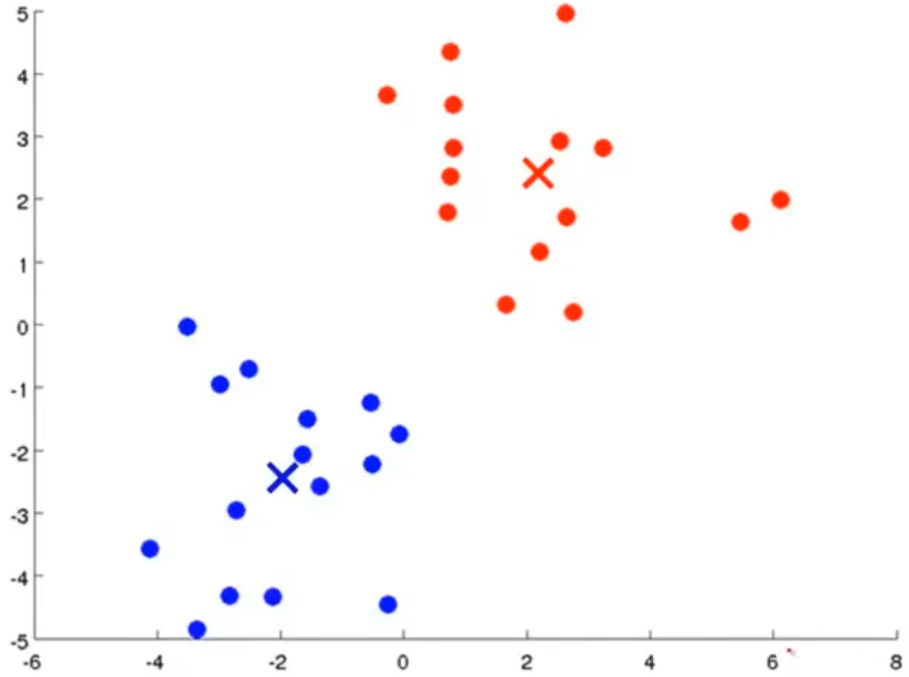
K均值算法的详细过程如下：
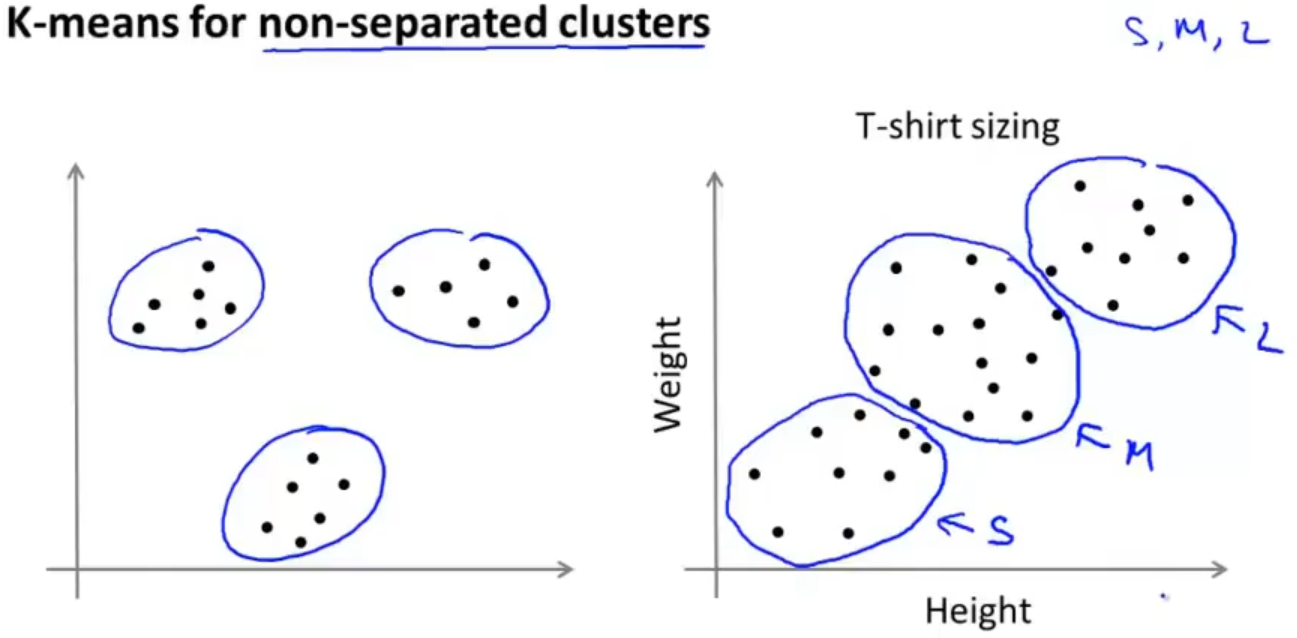
在分类情况不明确的情况，照样可以使用K均值算法
1.3 目标优化 Optimization objective
在监督学习中，线性回归和逻辑回归都有目标优化，最小化其代价函数。那其实在无监督学习中也是有的
在K均值算法中，目标优化就是要最小化所有数据点与其所关联的聚类中心点之间的距离之和，所以K均值的代价函数为：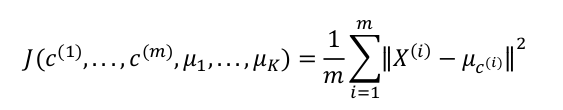
目标优化就是要使其最小化
对于K均值算法整体，也就是需要减小 c(i) 引起的代价和减小 μi 引起的代价
1.4 随机初始化 Random initialization
对于K均值聚类中心的选取，我们采用随机初始化的方式，随机初始化的方式有很多，最后认为一种方式的效率比较好一点，该方式为：
首先 K 值应该小于数据集的数量 m，然后从训练集中随机选取 K 个样本，把这个 K 个样本的数据作为这个 K 个聚类中心的数据的初始化
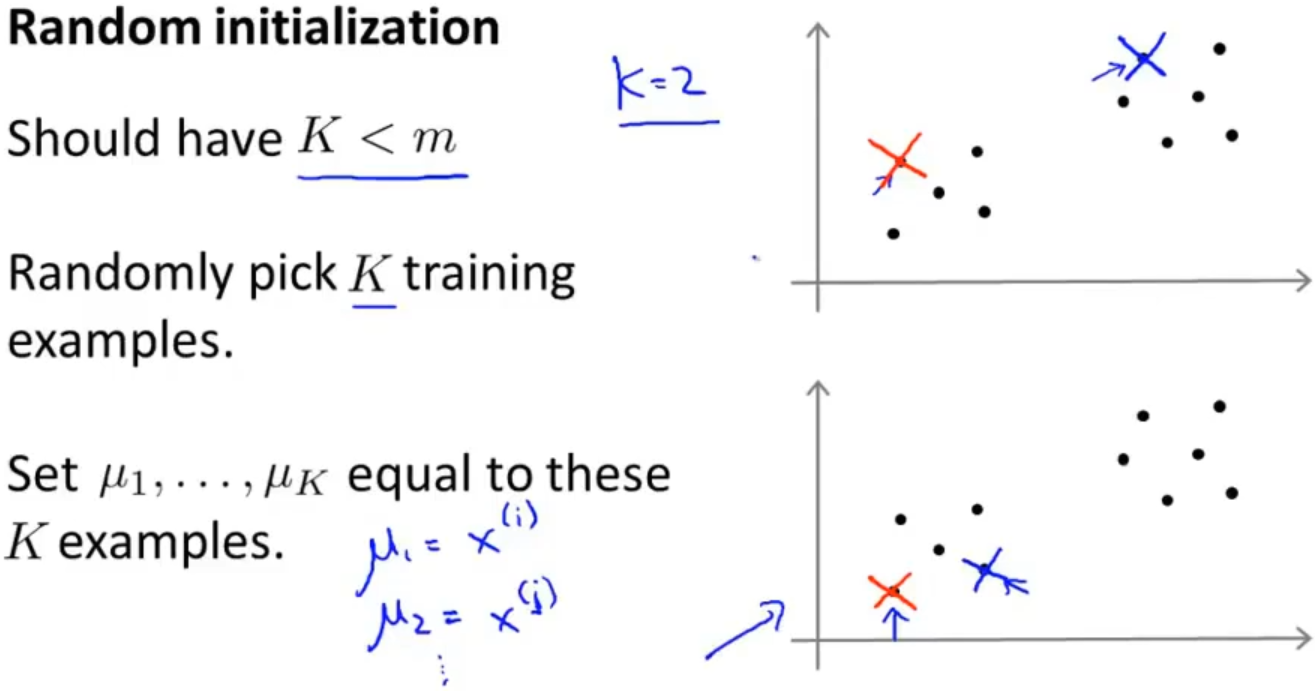
当然使用这种方式也有一点是不好的，就是初始化的时候有一些聚类中心是靠的很近的，这样就会导致分类的效果不尽如人意，如下图：
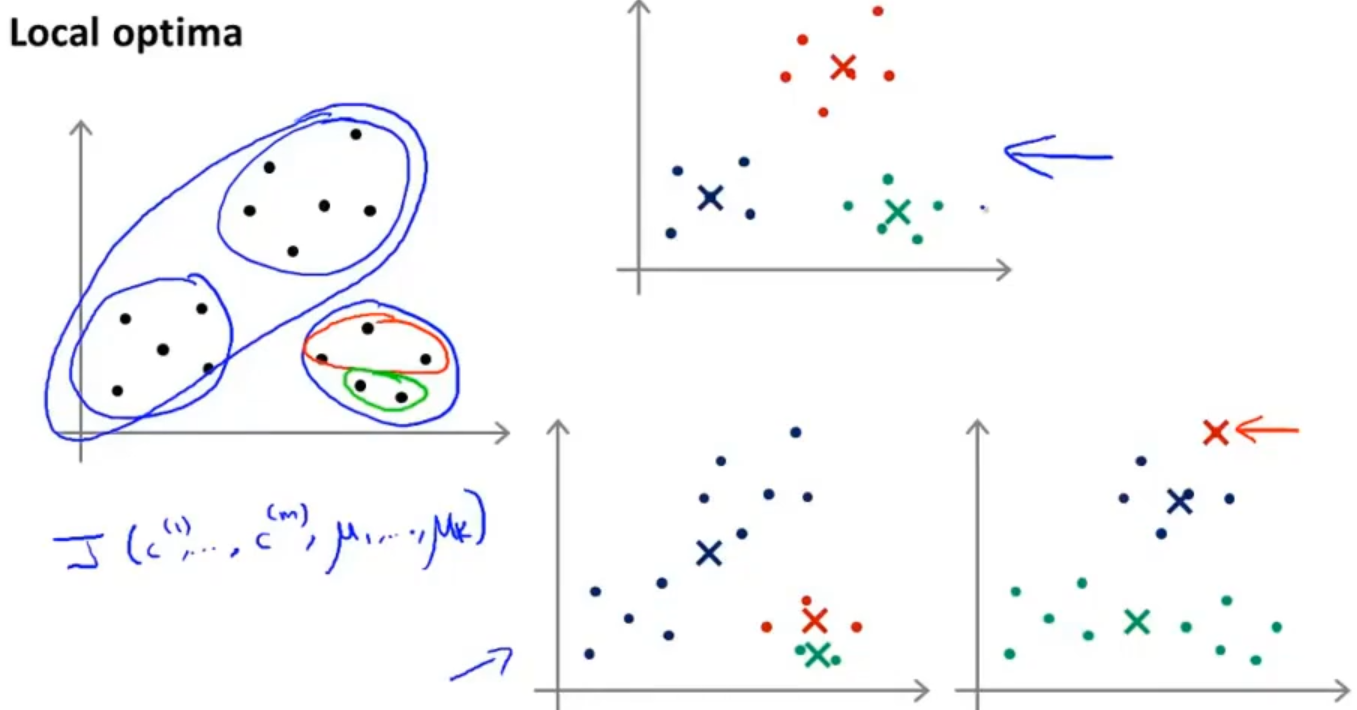
为了解决出现这种问题，我们采取多次运行K均值算法，每次都随机初始化聚类中心，最后选择代价函数最小的那一个，当然这个方式适用于 K 值较小的情况下
1.5 选择聚类数量 Choosing the number of clusters
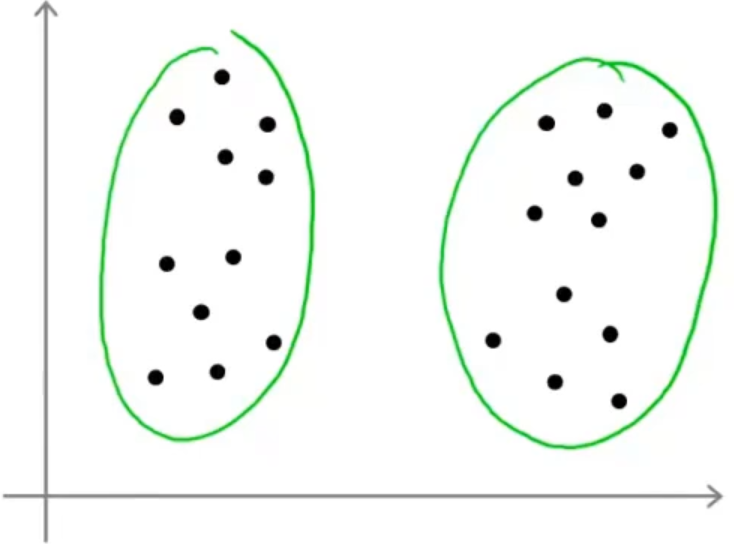
选择聚类数量也就是K均值算法中 K 值的选取，这就没有一个非常好的方式去选取了，因为具体问题还得具体分析，比如下图中的例子，我们可以选取2个聚类中心，也可以选取4个聚类中心
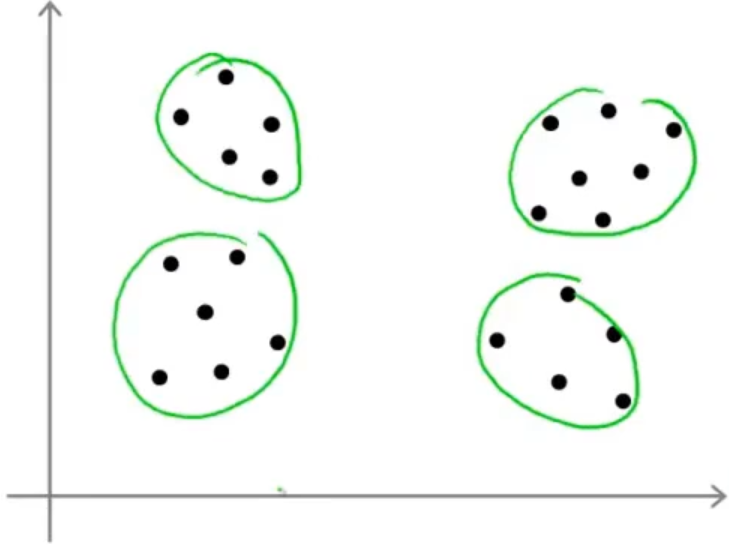
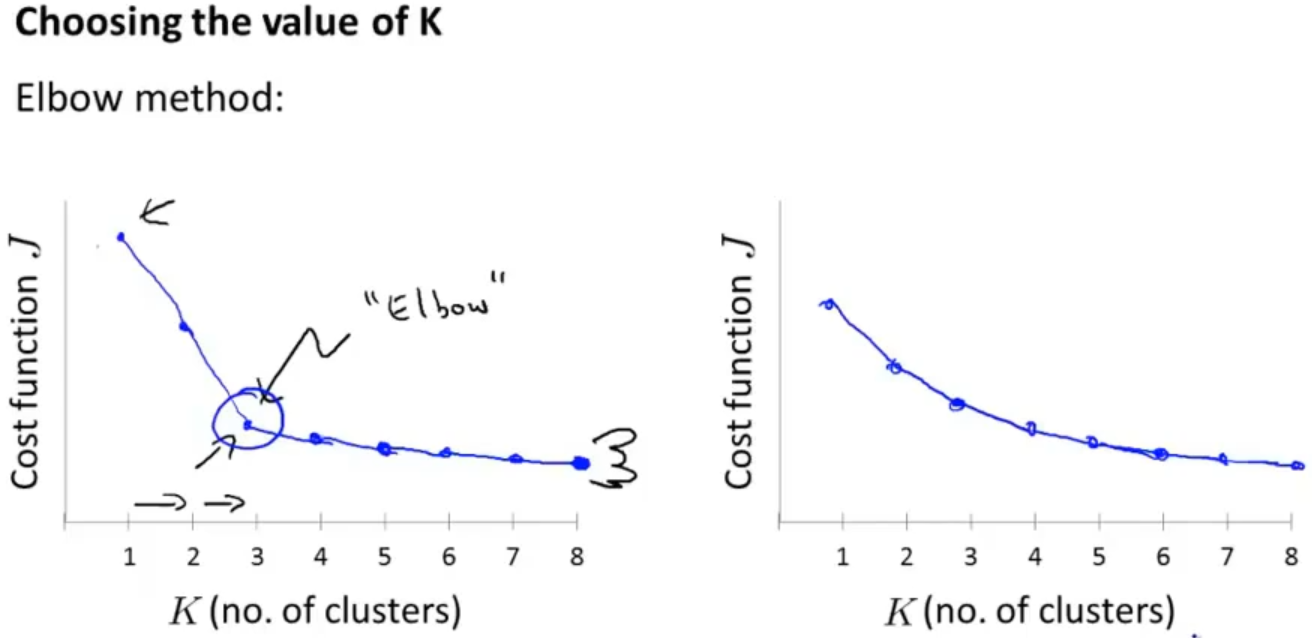
当然也存在一个方式来选择 K 值，它被称为"肘部法则"，以 K 值为横坐标，代价函数为纵坐标画出图像会得到一个类似于手臂的图像(如下左图)，那就可以认为在"肘部"(曲线的拐点)处可以取到最合适的 K 值。当然有时候会得到下右图这种结果，那么这个"肘部法则"就不太适用了
关于 K 值的选择，如果不能很好的运用"肘部法则"，那就需要具体问题具体分析了，采用人工选取，比如衣服尺码数量的选择，根据需求是需要 S,M,L 还是需要 XS,S,M,L,XL
