机器学习笔记10
支持向量机
1.1 优化目标 Optimization objective
与逻辑回归和神经网络相比,还有一种更加强大的算法是支持向量机(Support Vector Machine) ,它在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式并且广泛应用于工业界和学术界
我们通过回顾逻辑回归慢慢的引入支持向量机
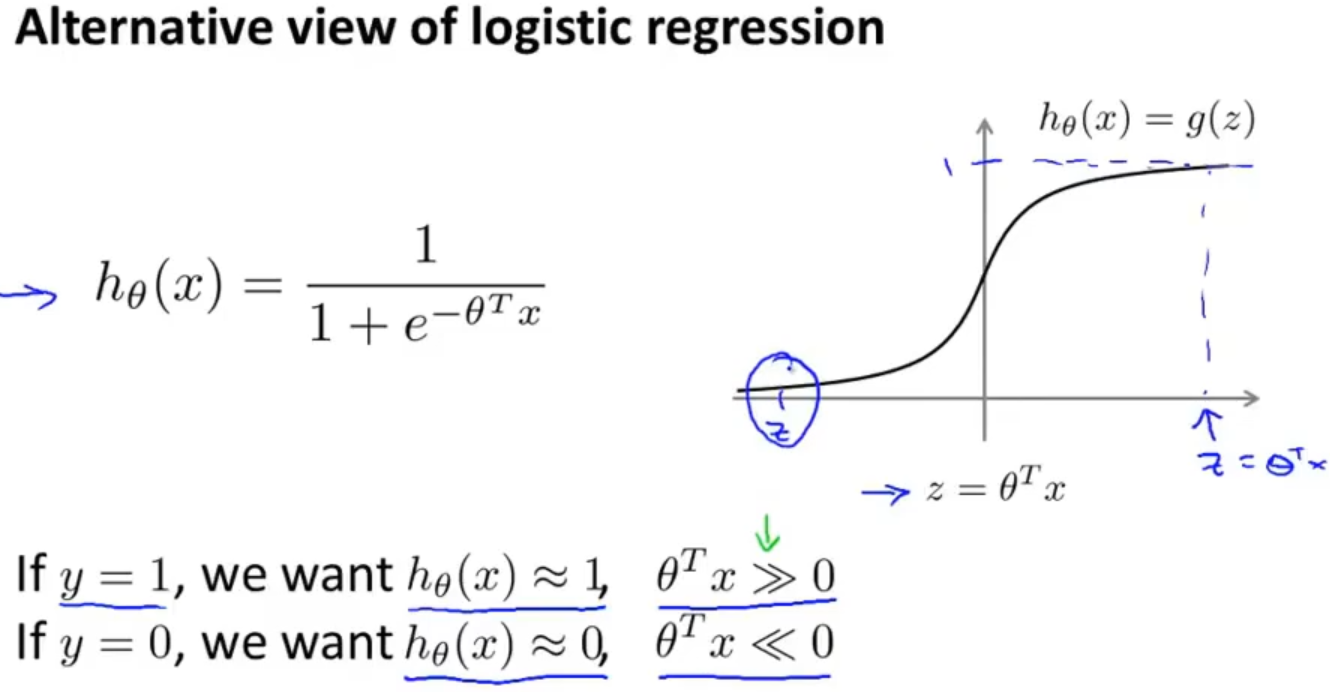
对于代价函数中的一部分来说需要做一些修改,假设只有一个数据样本,把 hθ(x)=1/(1+e-θTx) 带入公式,把 θTx看成是z,用灰色曲线作出图像
If y = 1, we want hθ(x) ≈ 1, z>>0;
If y = 0, we want hθ(x) ≈ 0, z<<0;
现在我们用玫瑰色曲线函数来代替灰色曲线函数。左边的玫瑰色曲线函数称为cost1(z),右边的玫瑰色曲线函数称为 cost0(z)
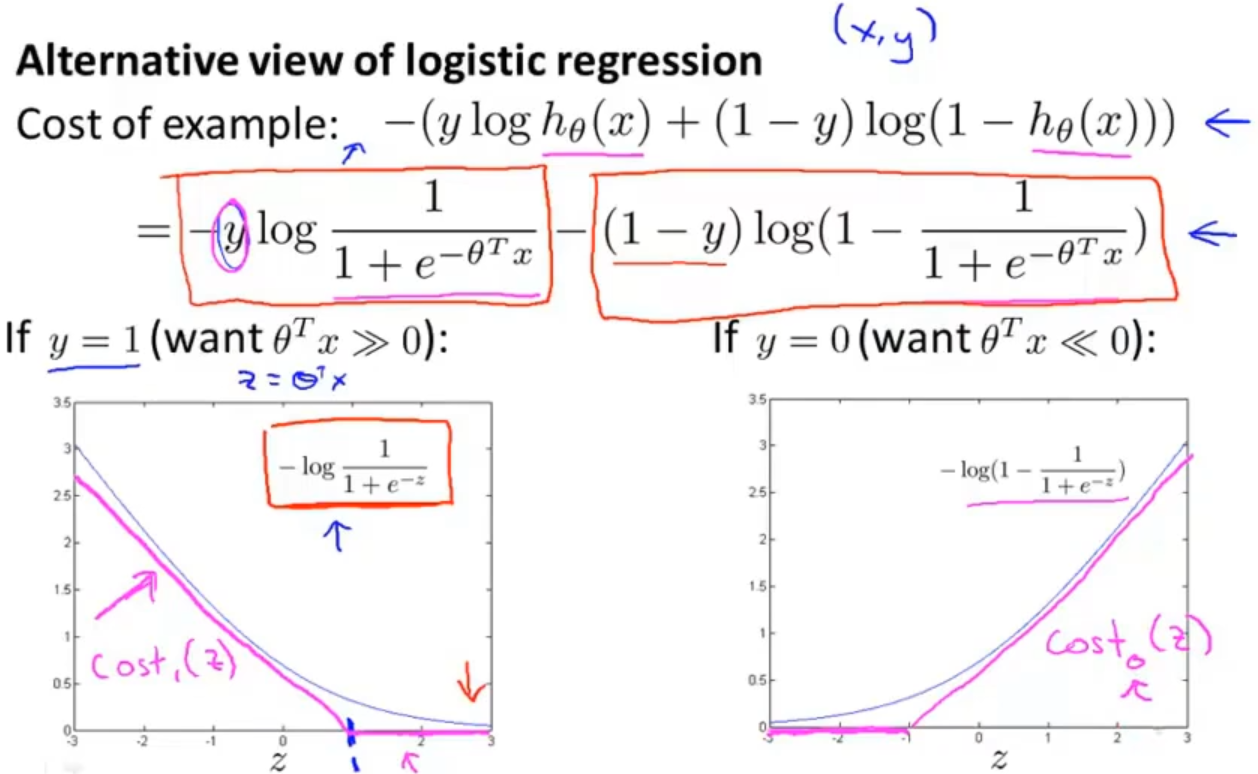
回到逻辑回归的代价函数中,对其进行修改转变为支持向量机的代价函数,把cost1(z)和cost0(z)替换掉原来的函数,同时对常数项也进行处理(处理常数项对求最优参数没有影响),先去掉 1 / m,再去掉 λ ,把代价函数整体看成 A + λB的形式,转变之后就变成 CA +B 的形式(其中 C = 1 / λ )
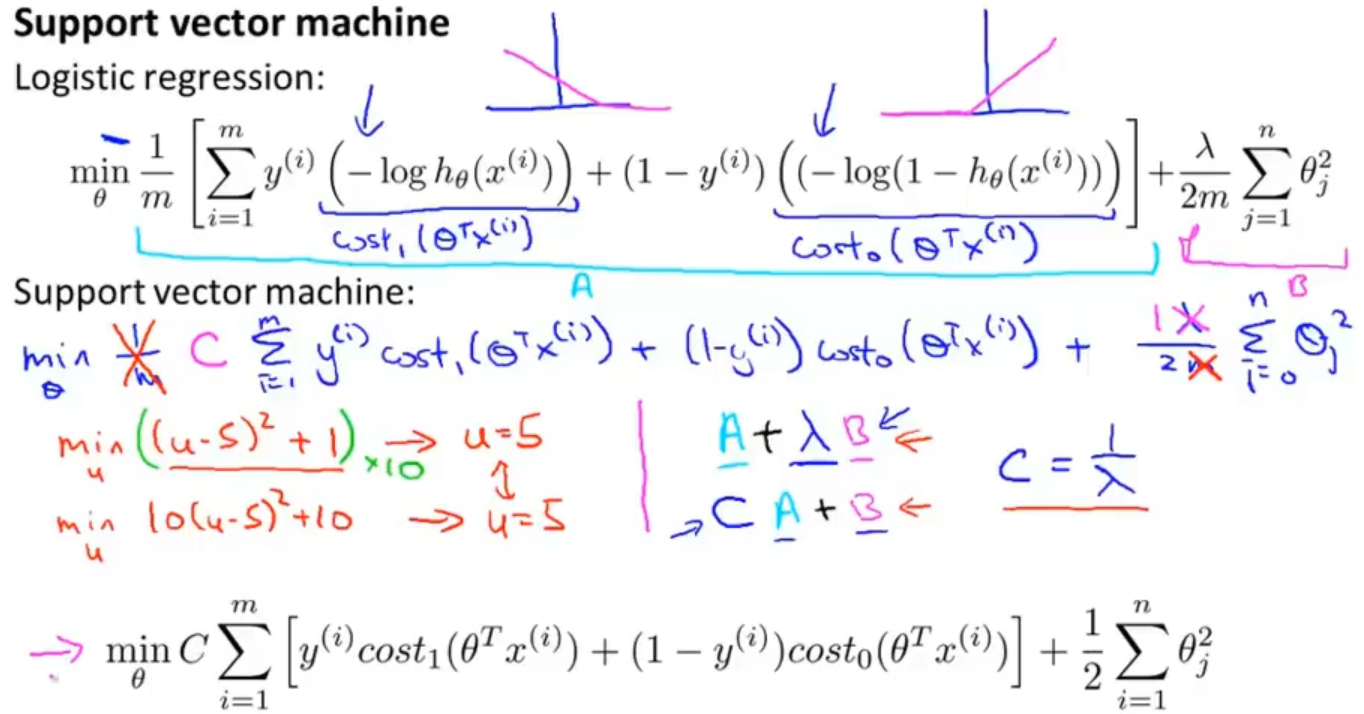
最后整理一下就可以得到支持向量机的代价函数,同时逻辑回归中假设的输出是一个概率值。 而 SVM 直接预测 y = 1,还是 y = 0
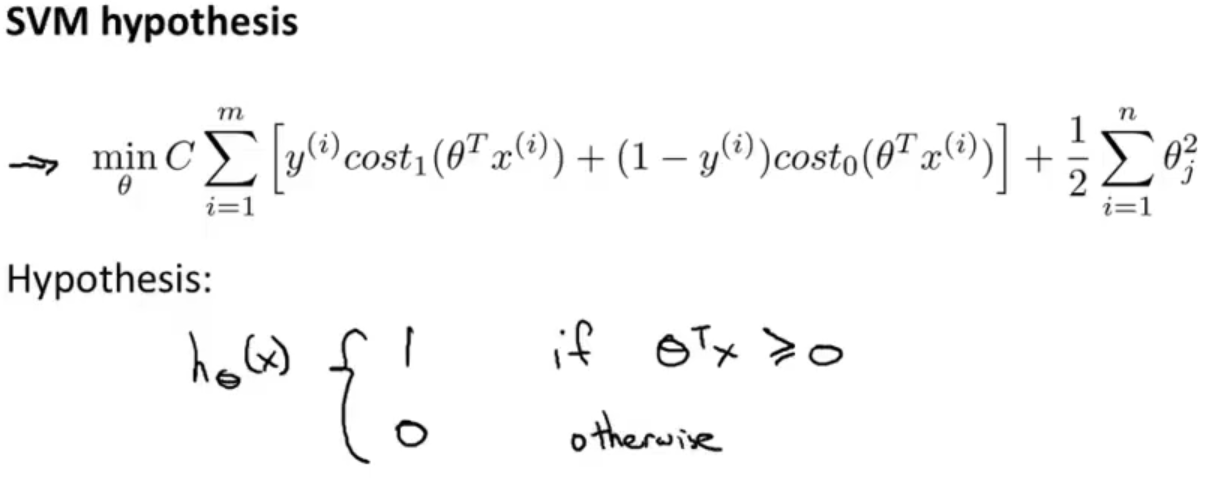
1.2 最大间隔的理解 Large Margin Intuition
如果C的数值比较大的话,想要最小化代价函数,那就需要最小化cost1(z)和cost0(z),从图像看出可以代价于当y=1时,z≥1,当y=0时,z≤-1

只有当C 特别大的时候, SVM 才是一个最大间隔分类器,那么当 C 特别大时,在优化过程中,第一项会接近于0,目标变为最小化第二项

支持向量机的最大间隔就是在两类之间有许多的决策边界,需要找到一条边界使得margin最大,如下图
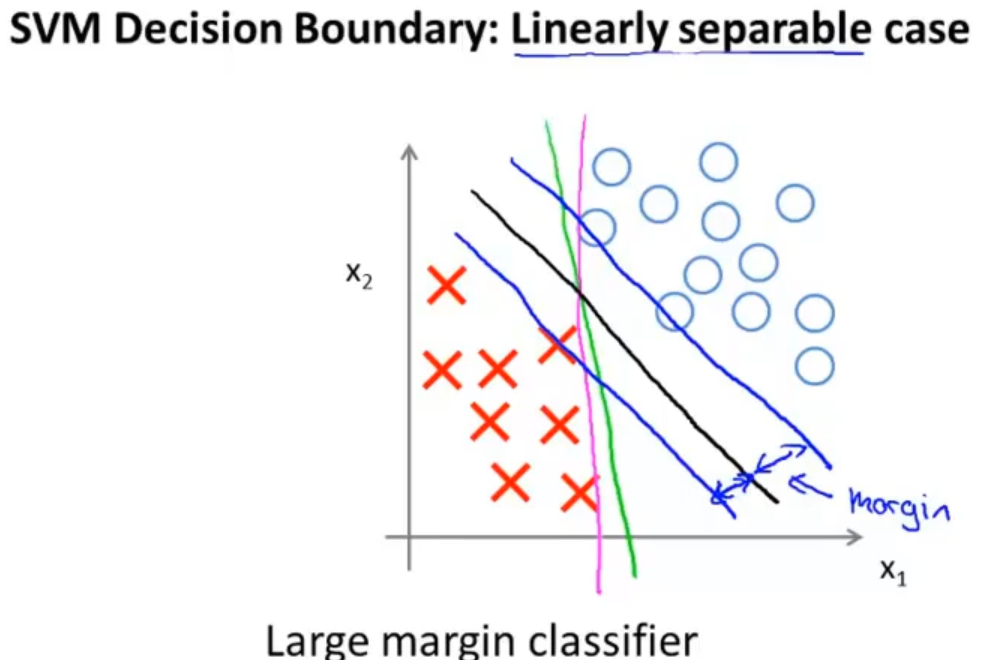
对于有异常值的支持向量机来说,如果想将样本用最大间距分开,即将 C 设置的很大。那么仅因为一个异常点,决策边界会从黑线变成那条粉线,这实在是不明智的,如果 C 设置的小一点,最终得到这条黑线。它可以忽略一些异常点的影响,而且当数据线性不可分的时候,也可以将它们恰当分开,得到更好地决策边界
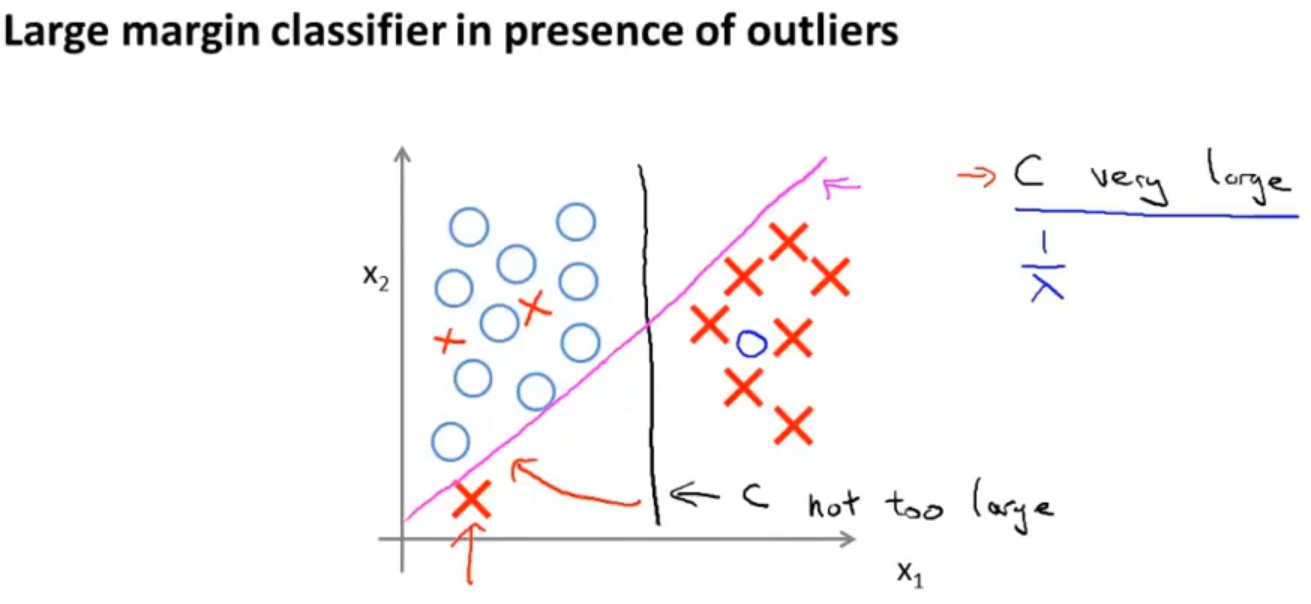
值得注意的是,因为 C = 1 / λ,因此C 较小时,相当于 λ 较大。可能会导致欠拟合,相当于高偏差 ,C 较大时,相当于 λ 较小。可能会导致过拟合,相当于高方差
1.3 大间距分类背后的数学 The mathematics behind large margin classification
1.3.1 向量内积
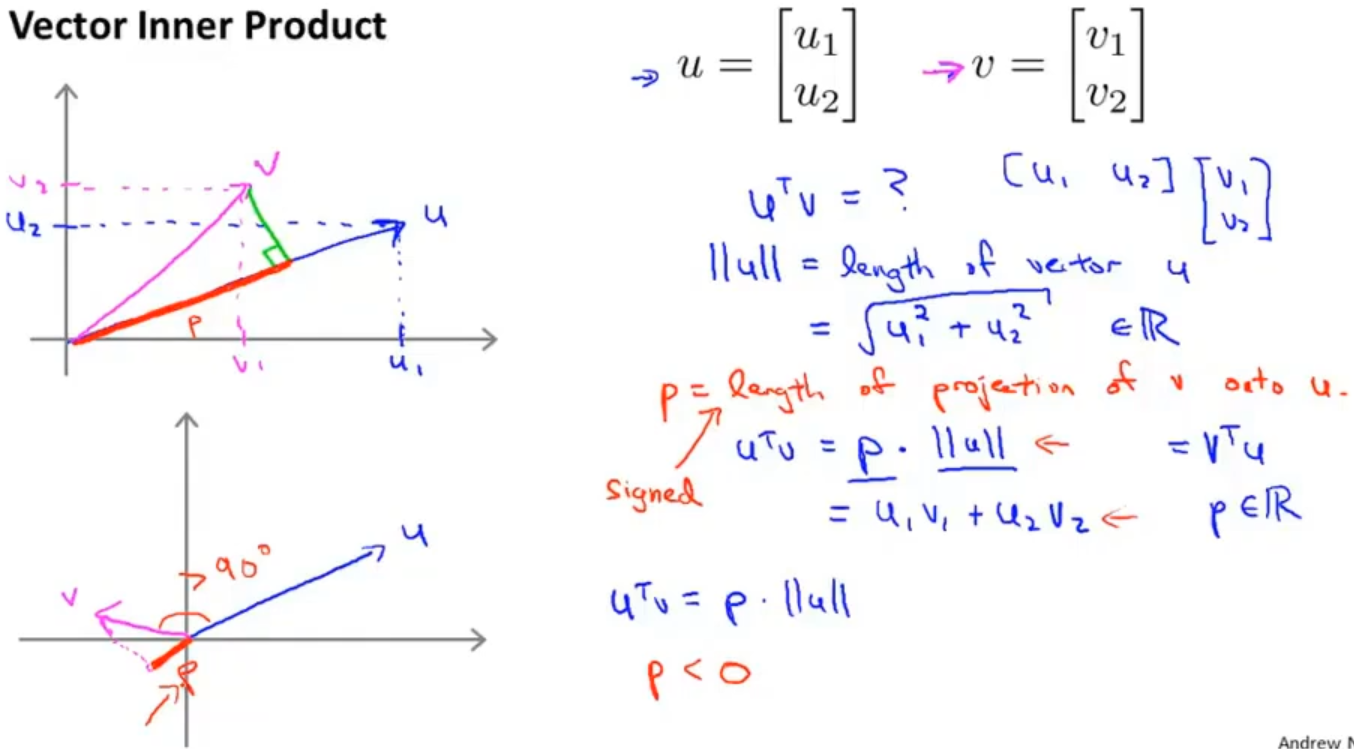
向量内积: 两个向量 u 和 v ,uTv 就叫做向量 u 和 v 之间的内积,∥u∥ 表示 u 的范数norm,也就是向量 u 的欧几里得长度( √(u12+u22) ),属于一个实数
在这里,内积可以用两种方式表示:
第一种是通过投影的方式计算,uTv = ||u|| · ||v|| · cosθ = ||u|| · p (p也是属于一个实数,如果p是向量反向上的投影则p<0)
第二种是通过矩阵乘法的方式计算,uTv = u1 × v1 + u2 × v2 = vTu
1.3.2 SVM 代价函数的另一种理解方式
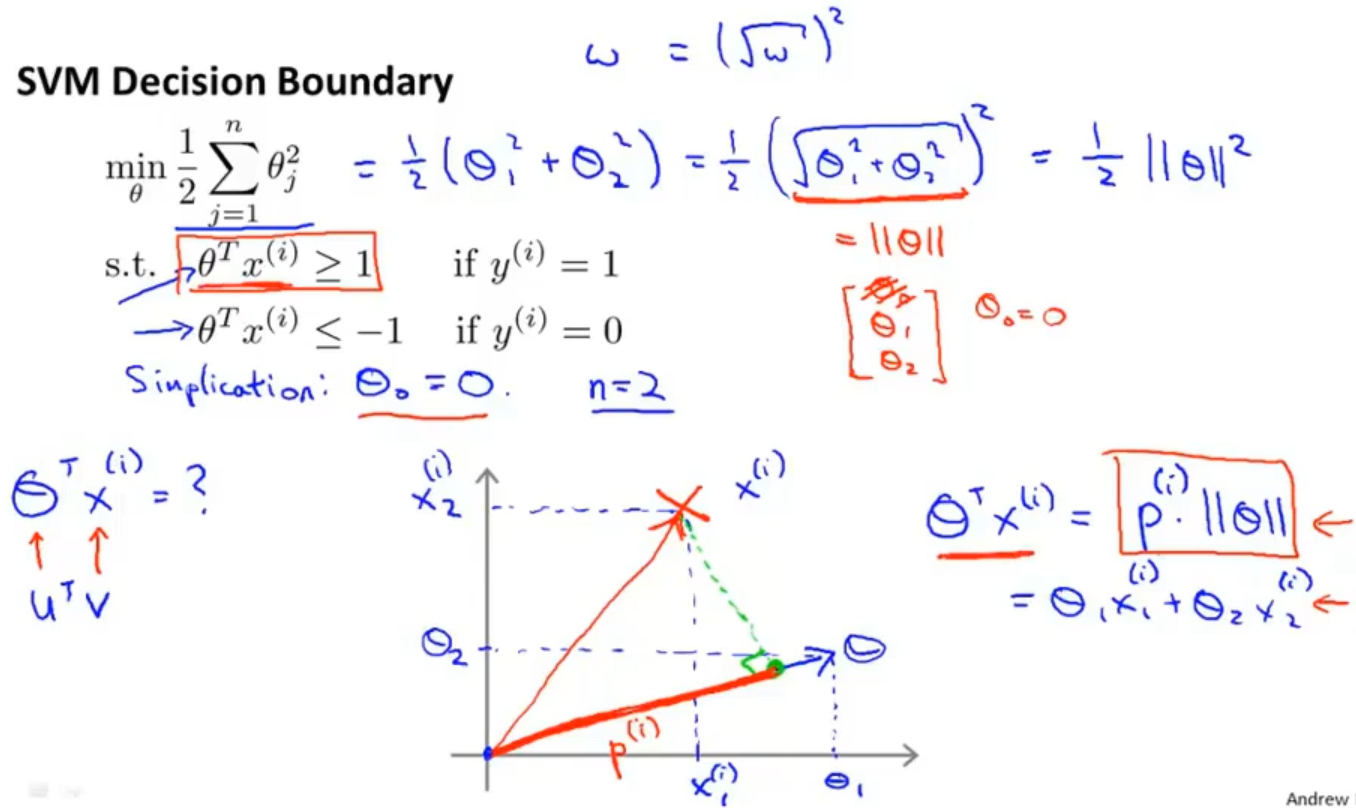
有了内积的知识,对支持向量机的代价函数我们就有了另一种理解方式,在之前说到的代价函数中如果将C设的很大,代价函数只剩下后面的那项,假设θ0=0,参数个数n=2,可以代价函数进行转变成J(θ) = 1/2 × ||θ||^2,θT和x(i)看成之前讲的向量uT和v, 这样就可以得到 θTx = p · ||θ|| (p 是 x 在 θ 上的投影)
1.3.3 选择更优的决策边界
如果我选择绿色直线作为决策边界,那么蓝色直线就是参数向量了(根据线性方程中法向量的知识),那么可以看每个数据在参数向量上的投影都非常的短
对于正样本 x(1) 而言,想要p(1) ⋅ ∥θ∥ >= 1,现在 p(1) 长度非常短,就意味着 ||θ|| 需要非常大
对于负样本 x(2) 而言,想要p(1) ⋅∥θ∥ <= −1,现在p(2) 长度非常短,就意味着 ||θ|| 需要非常大
但我们的目标函数是希望最小化参数 θ 的范数,因此我们希望: 投影长度 p(i) 尽可能大
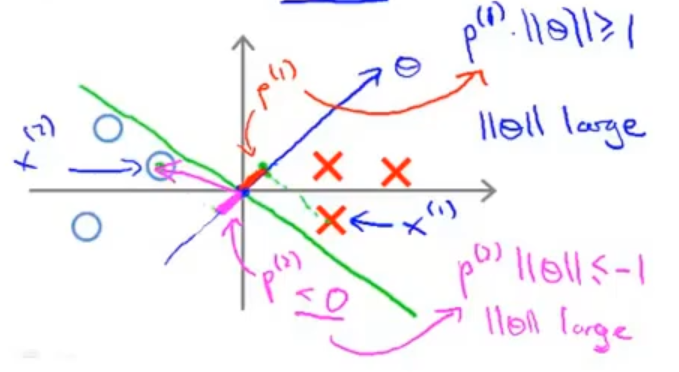
如果我们换一个决策边界,那么就可以看到每一个数据在参数向量上的投影都非常的长,这正是我们在目标函数中希望最小化参数 θ 的范数
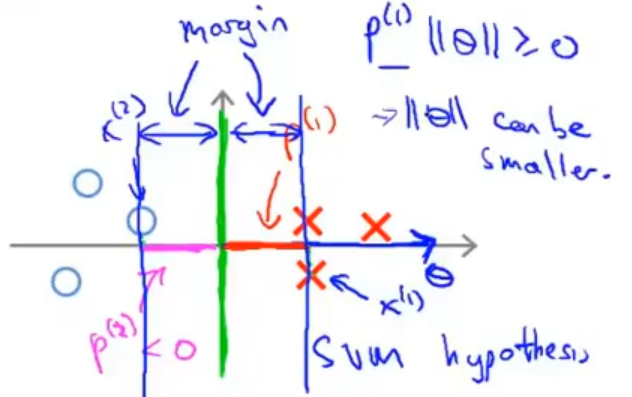
以上都是讨论在θ0 = 0的情况下,θ0 = 0的意思是我们让决策界通过原点。如果θ0 ≠ 0,决策边界不过原点 ,结论同样成立
1.4 核函数 Kernels
1.4.1 Kernels I
对于这种非线性分类问题,可以采用高级数的多项式模型来解决,在该模型中我们会把特征 x 用新特征 f 来替代,比如: f1 = x1 , f2 = x2 , f3 = x1 x2 , f4 = x12 ...
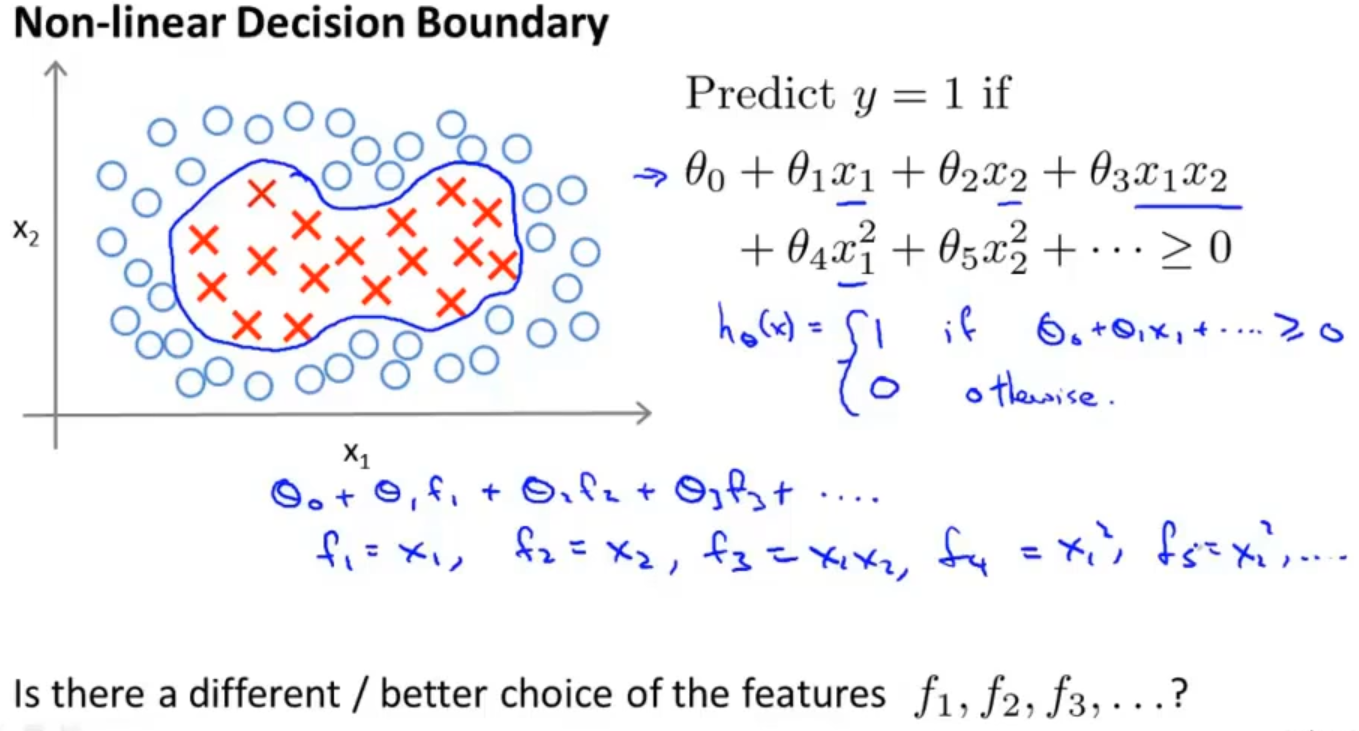
在构建新特征 f1 , f2 , f3 的时候还有没有更好的方法呢?其实是有的,我们可以通过核函数来构建新特征
来看一下下图中的例子,假设给定一个训练实例 x ,我们通过 x 与预先选定的 landmarks l(1) , l(2) , l(3) 的近似程度来计算新的特征
计算方式:fi = similarity(x, l (i) ) = exp( -( ||x − l (i) || )2 / 2σ2 ),这其实就是用了高斯函数,其中i为landmarks 的索引,||x − l (i) || 为实例 x 中所有特征与 landmark l(i) 距离的和,与之前说的|| w ||相似

如果一个训练实例 x 与 l 很近,则 f ≈ e−0 ≈ 1;与 l 很远,则 f ≈ e−( 较大的数 ) ≈ 0。 具体的计算如下:

通过一个例子,以水平面的坐标为 x1, x 2 ,垂直坐标轴为 f 构建3D图像和等高线图来观察一下对于不同的 σ 对 f 的影响

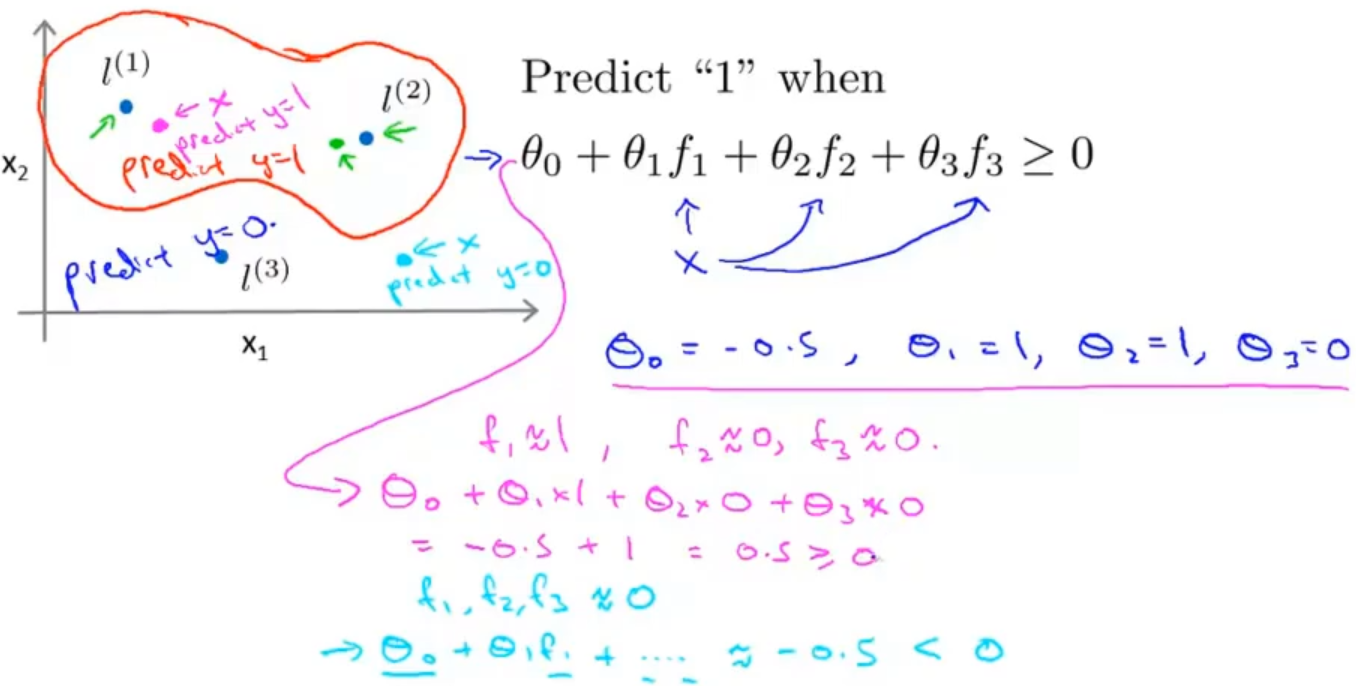
假设θ0 = -0.5,θ1 = 1,θ2 = 1,θ3 = 0,那粉色点离 l (1) 更近,所以 f1 接近 1,而 f2 ,f3 接近 0。因此h θ(x) ≥ 0,因此预测y = 1;同理,绿色点离 l(2) 较近的,也预测y = 1;但蓝绿色点离三个 landmark 都较远,预测y = 0
那图中红色封闭曲线就可以组成决策边界了,在整个预测过程中,我们采用的特征不是训练实例本身的特征,而是通过核函数计算出的新特征f1 , f2 , f3
1.4.1 Kernels II
之前在选择landmark的时候我们是随便选择三个点的,那在实际应用中我们是如何获得landmark的呢?
我们是把训练集中的数据点直接作为landmark,这样 l(i) 就会对应训练集中 x(i),相当于把 l(i) 初始化为 x(i)
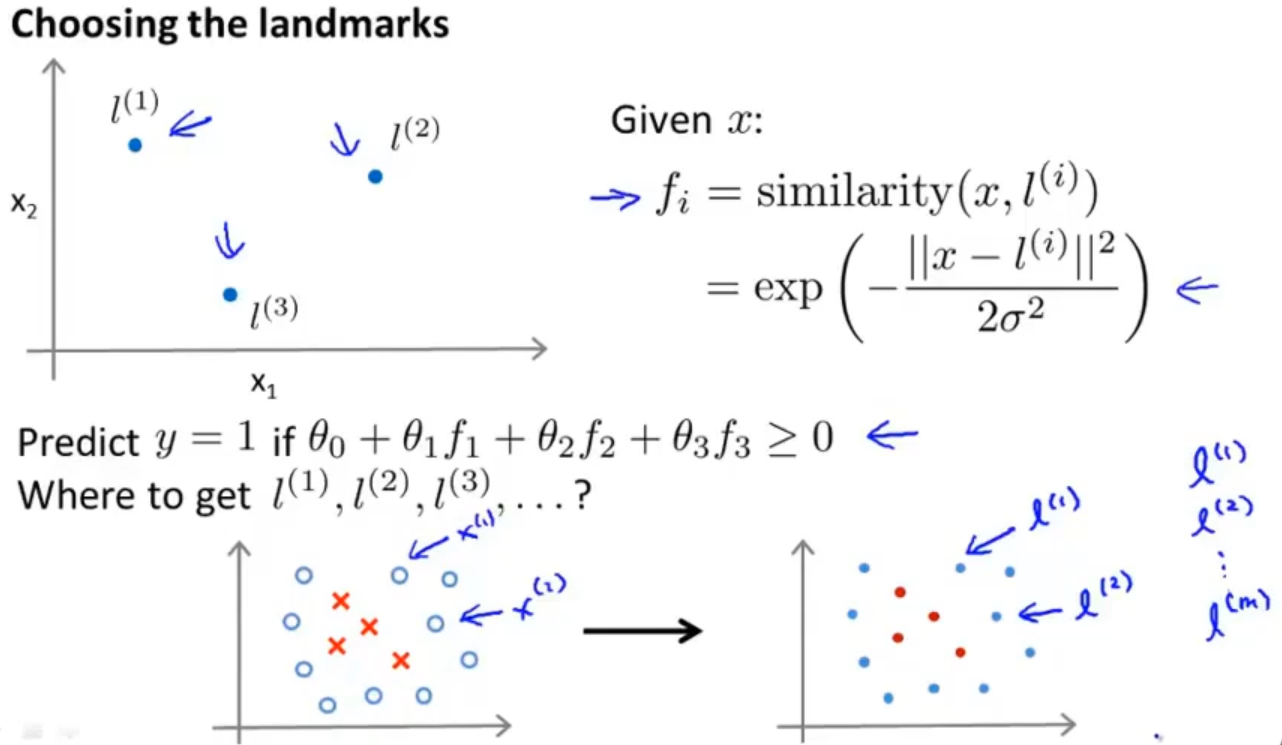
对于将 l(i) 初始化为 x(i) ,这么做的好处是得到的新特征是建立在 原有特征 与 训练集中其他原有特征之间距离 的基础之上的
新特征 f 向量与原特征向量的形式保持一致,在初始化时,添加 f0 = 1

将核函数引入支持向量机的代价函数中,用新特征 f 替换掉原特征 x,预测一个实例 x 对应结果的方法是:给定x,计算新特征 f,当 θTf >= 0 时预测 y = 1; 否则反之
同时在计算上,为了简化计算, 在计算正则项 θTθ 时,用 θTMθ 代替 θTθ ,其中 M 是一个矩阵,核函数不同则M不同

整理一下在使用核函数的支持向量机时遇到的两个参数(C和σ)对新特征 f 的影响:
当 C 较大,相当于 λ 小,可能会导致过拟合,高方差
当 C 较小,相当于 λ 大,可能会导致欠拟合,高偏差
当 σ 较大时,图像缓和,可能会导致低方差,高偏差
当 σ 较小时,图像陡峭,可能会导致低偏差,高方差

1.5 使用支持向量机 Using an SVM
在使用支持向量机来求解参数θ的时候,我们通常会通过调包的方式去完成,除此之外,我们还需要选择一个合适的参数C和是否选择使用核函数,如果选择使用核函数,那就还需要注意一点别的东西(比如使用高斯函数作为核函数的时候,我们就需要选择一个合适的参数σ)

如果是使用高斯函数,那么还需要注意的是特征的放缩,就比如在房屋价格预测的例子中,房屋尺寸大小和房屋数量显然就不是一个数量级的,如果不进行特征放缩的话,那房屋数量这个特征的影响力可能就很小了

当然除了高斯函数以外也有别的函数,比如多项式核函数(Polynomial Kernel), 字符串核函数(String kernel), 卡方核函数( chi-square kernel) ,直方图交集核函数(histogram intersection kernel) 等。它们的目标也都是根据训练集和地标之间的距离来构建新特征,只是高斯函数是属于比较常用的函数

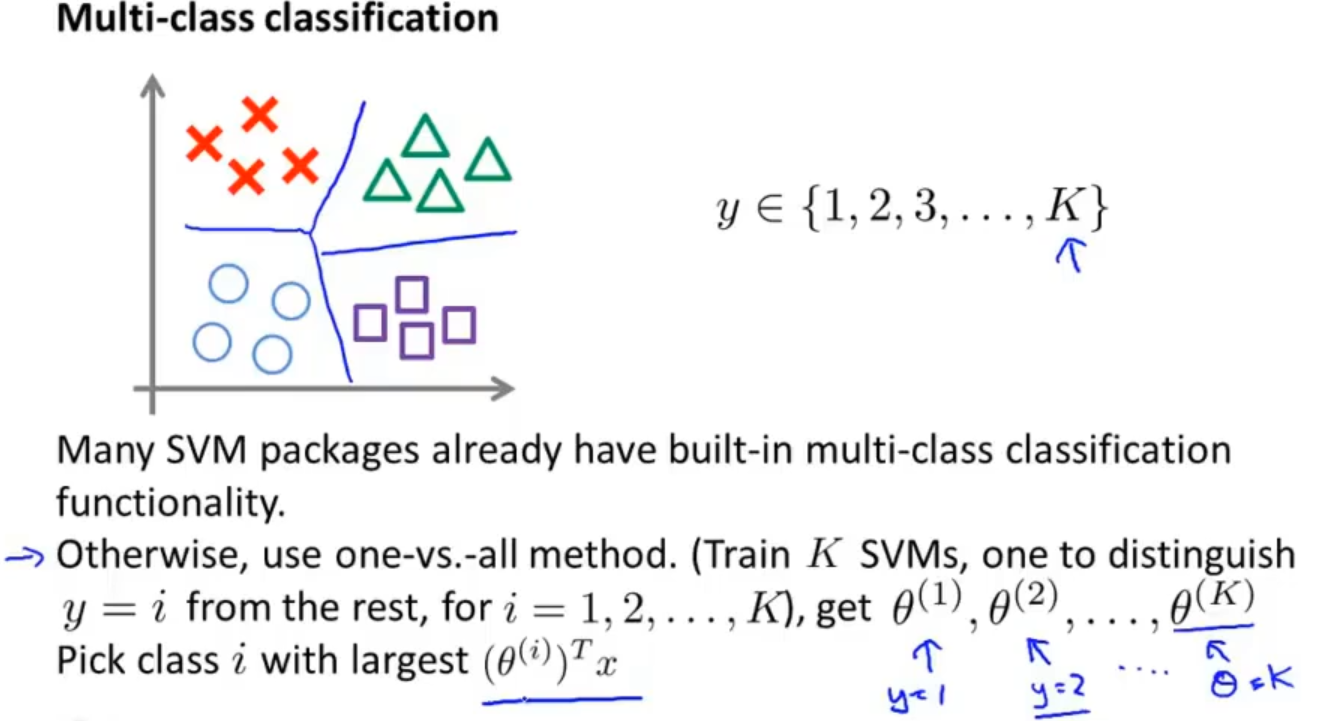
在多分类问题上,可以训练K个支持向量机来解决问题,不过大多数的支持向量机包已经构建好了多分类功能了
对于模型的选择上还需要根据实际的情况来选择,假设有n个特征,m个训练样本
如果 n » m,即训练集数据量不够支持我们训练一个复杂的非线性模型,选用逻辑回归模型或者不带核函数的 SVM。
如果 n较小,m中等,例如n在 1-1000 之间,而m在 10-10000 之间,使用高斯核函数的 SVM。(如果训练集非常大,高斯核函数的SVM 会非常慢)
如果 n较小,m较大,例如n在 1-1000 之间,而m大于 50000,则使用 SVM 会非常慢。解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的 SVM
其实逻辑回归和不带核函数的SVM 非常相似,不过具体还得根据实际情况来选择

如果是使用神经网络的话,神经网络的效果可能会比支持向量机更好,但是神经网络的缺点就是训练太慢了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号