机器学习笔记8
机器学习应用建议
1.1 决定下一步做什么 Deciding what to try next
当你使用一个模型进行测试后发现得到结果与真实值差异太大的时候，我们下一步该怎么办？
1. 获得更多的训练样本，2. 尝试缩小特征数，3. 尝试增大特征数，4. 尝试添加多项式的特征，5. 减小λ，6. 增大λ
那这么多方法如果我们一个一个的去尝试就太耗时间，所以就引入机器学习诊断来帮助我们
机器学习诊断法可以告诉你问题出在哪里，也可以告诉你需要用什么样的办法去尝试
机器学习诊断法的定义如下：
1.2 评估假设 Evaluating a hypothesis
评估假设是评估算法学习得到的假设
如果我们得到一个很小的训练误差，就可以算是得到了一个很好的假设了吗？其实并不是这样的，在过拟合问题中我们深有体会
那怎么判断一个假设是否过拟合呢？对于一个简单的例子比如就两个特征，我们可以通过画图来判断
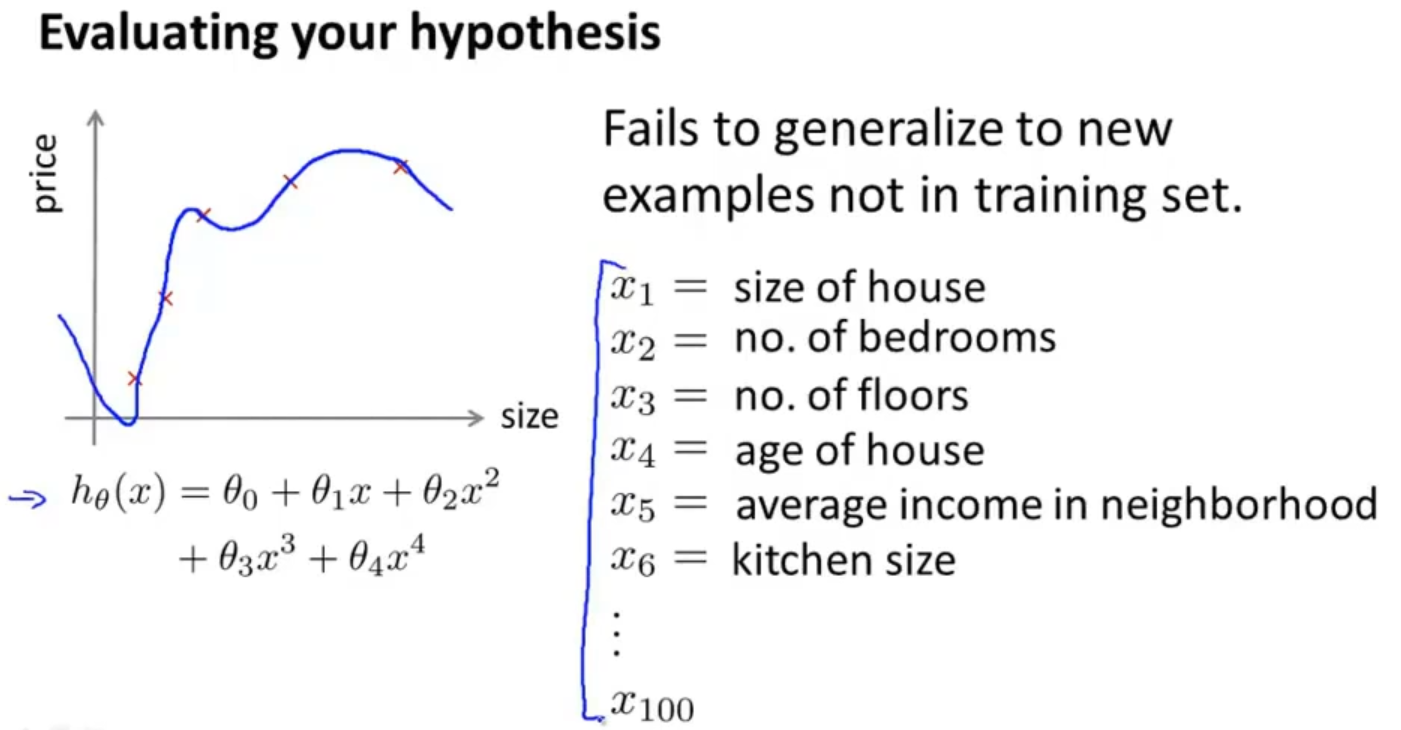
也可以通过标准的方式
首先需要将数据集进行处理，如果是随机分布的数据集那就按照7：3分成训练集和测试集，如果不是最好先转为随机分布，或者在划分训练集和测试集的时候随机抽取
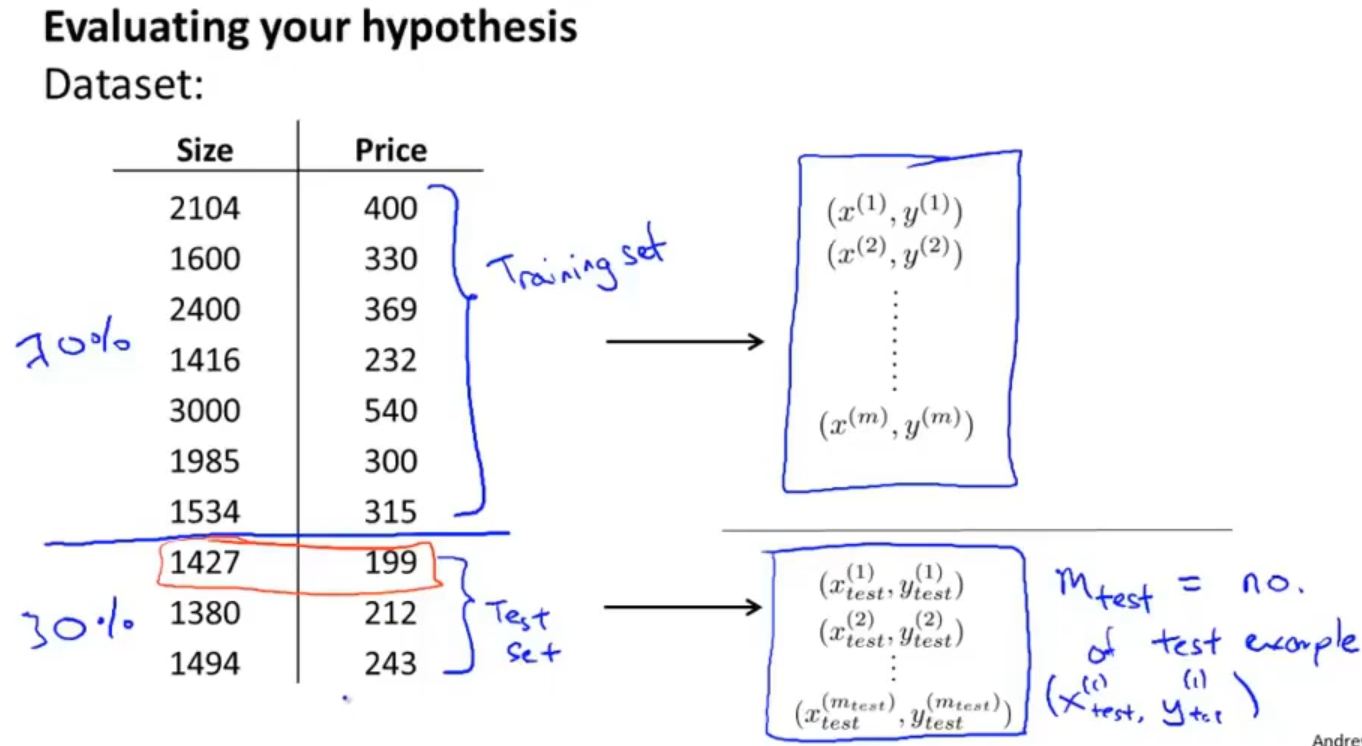
然后就是在计算误差中也要相应分别对训练集和测试集做误差计算
在回归问题中线性回归做误差计算：
在分类问题中逻辑回归做误差计算：
还可以通过错分率来计算误差，它是根据预测结果与真是结果做比对，预测错err值为1，预测对了err值为0来计算误差
1.3 模型选择和训练、验证、测试集 Model selection and training/validation/test sets
在过拟合中，如果用一些参数去拟合训练集，计算出来的训练误差并不能很好的估计实际的泛化误差
还有一个问题就是关于模型的选择应该如何去选择，比如提供以下十种模型，首先会先通过训练集计算出 θ，然后通过测试集计算误差，分别得到 Jtest(θ(1)),...Jtest(θ(10))，假设计算后发现Jtest(θ(5))的值最小，就选择这个模型，那如果我们再去使用测试集去评估这个模型的话就不能得到真正的评估结果了
为了解决这个问题我们将数据集重新划分成训练、验证、测试集，这样我们就可以通过验证集来计算误差，最后再使用测试集来评估模型，就不会得到一个比较靠谱的评估结果了
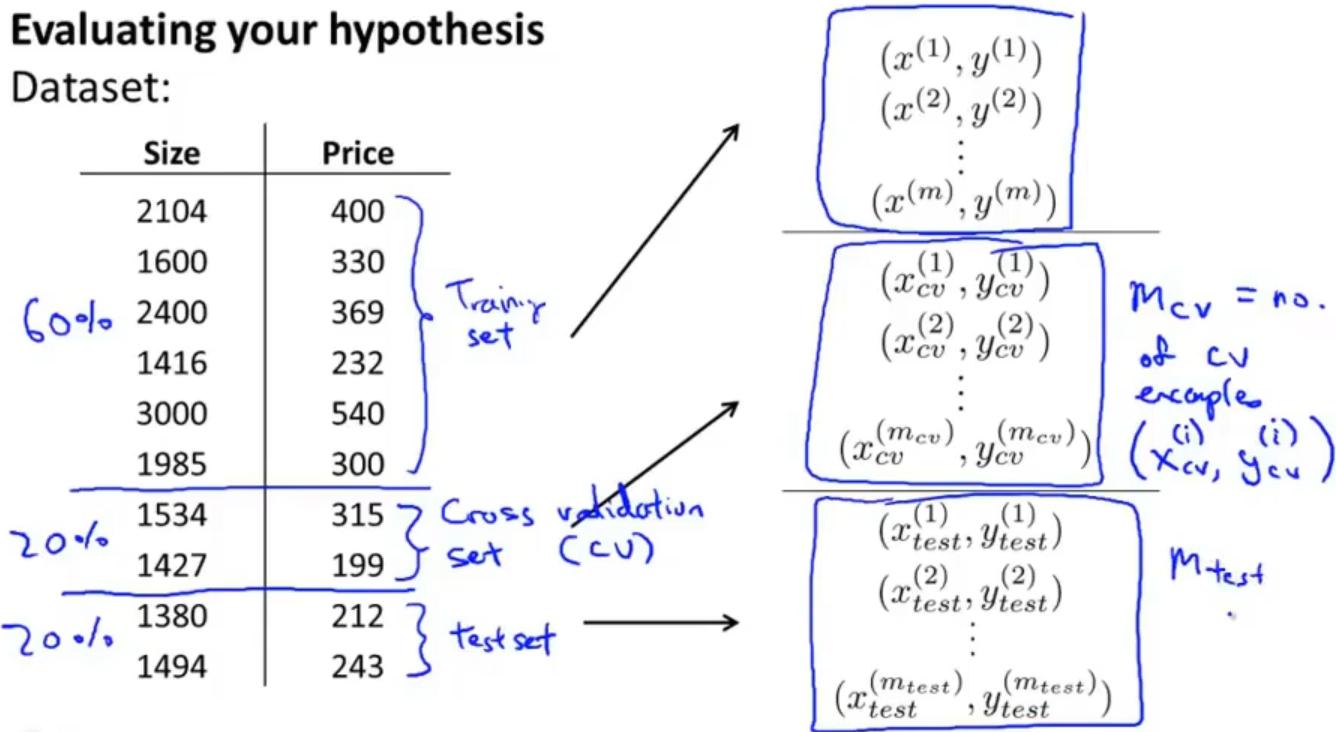
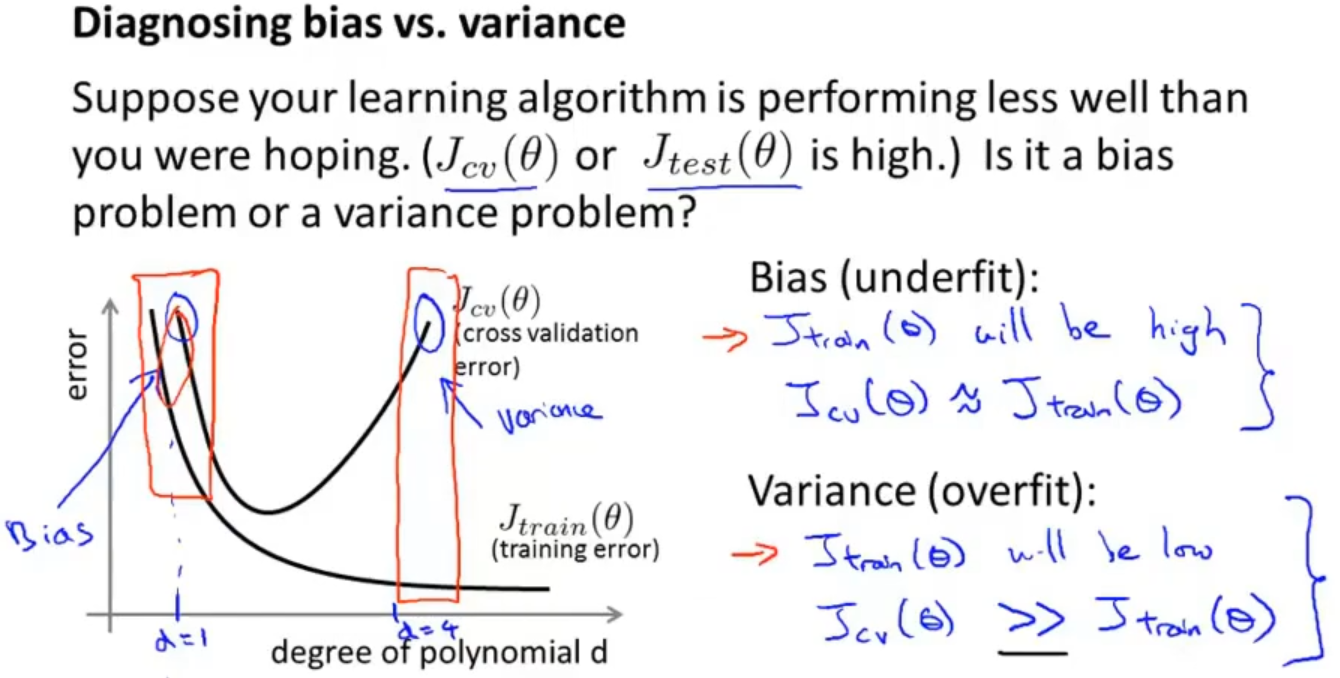
1.4 诊断偏差与方差 Diagnosing bias vs. variance
如果模型的表现不好，那大概率就是欠拟合和过拟合的问题，详细理解，如果误差过大，会导致欠拟合，如果方差过大，会导致过拟合
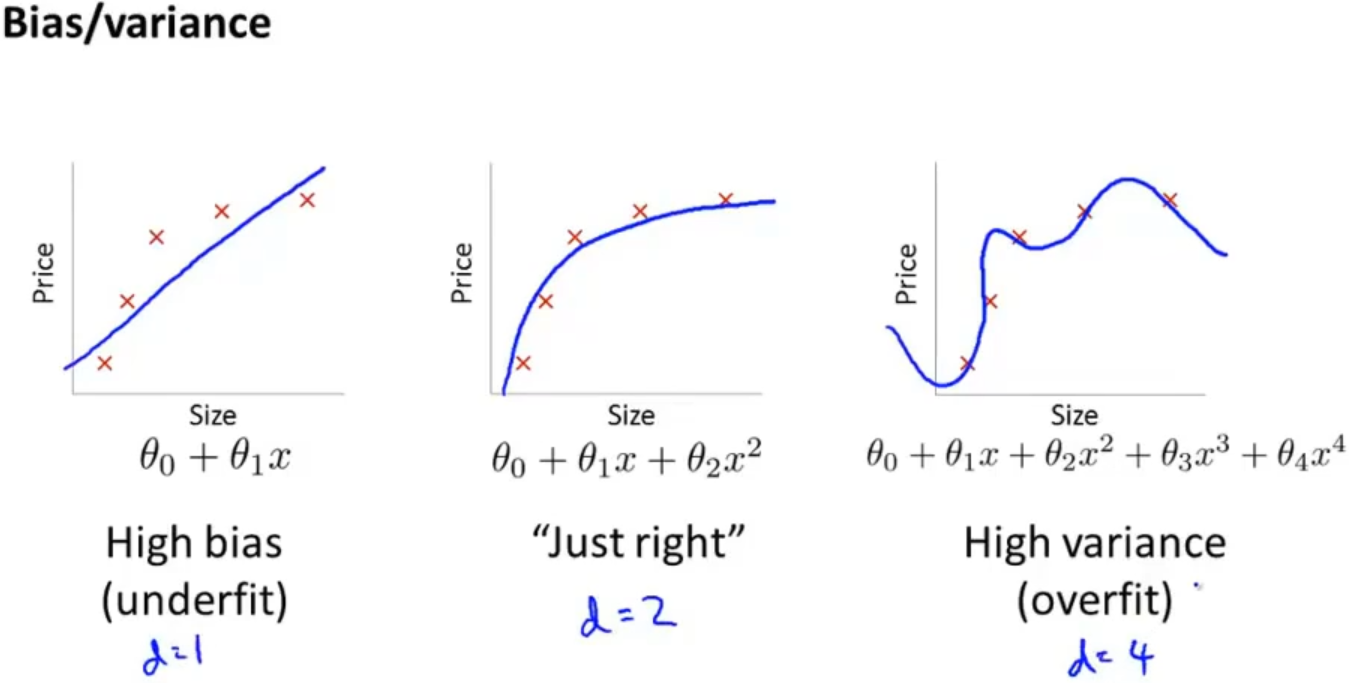
进一步分析，以多项式的次数d为横坐标，误差为纵坐标作图，可以得到下图
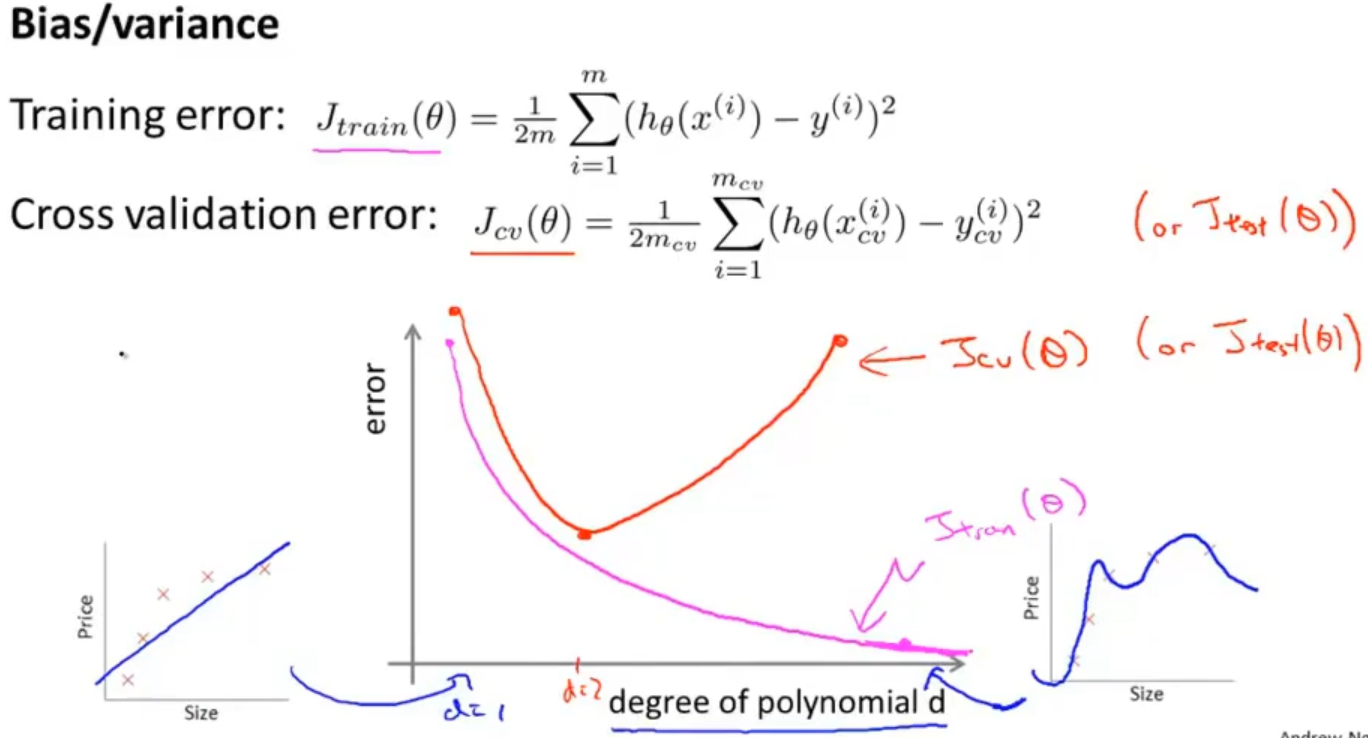
分析一下图像来判断模型是高误差(欠拟合)、还是高方差(过拟合)
当d=1的时候训练误差和验证(cv)误差都比较大，说明模型是欠拟合
当d=4的时候训练误差比较小，验证(cv)误差比较大，说明模型是欠拟合
1.5 正则化和偏差、方差 Regularization and bias/variance
在之前讲解线性回归中加入正则项的时候有说到选择一个合适的参数λ是很关键的，如果λ过小容易过拟合，如果λ过大欠拟合
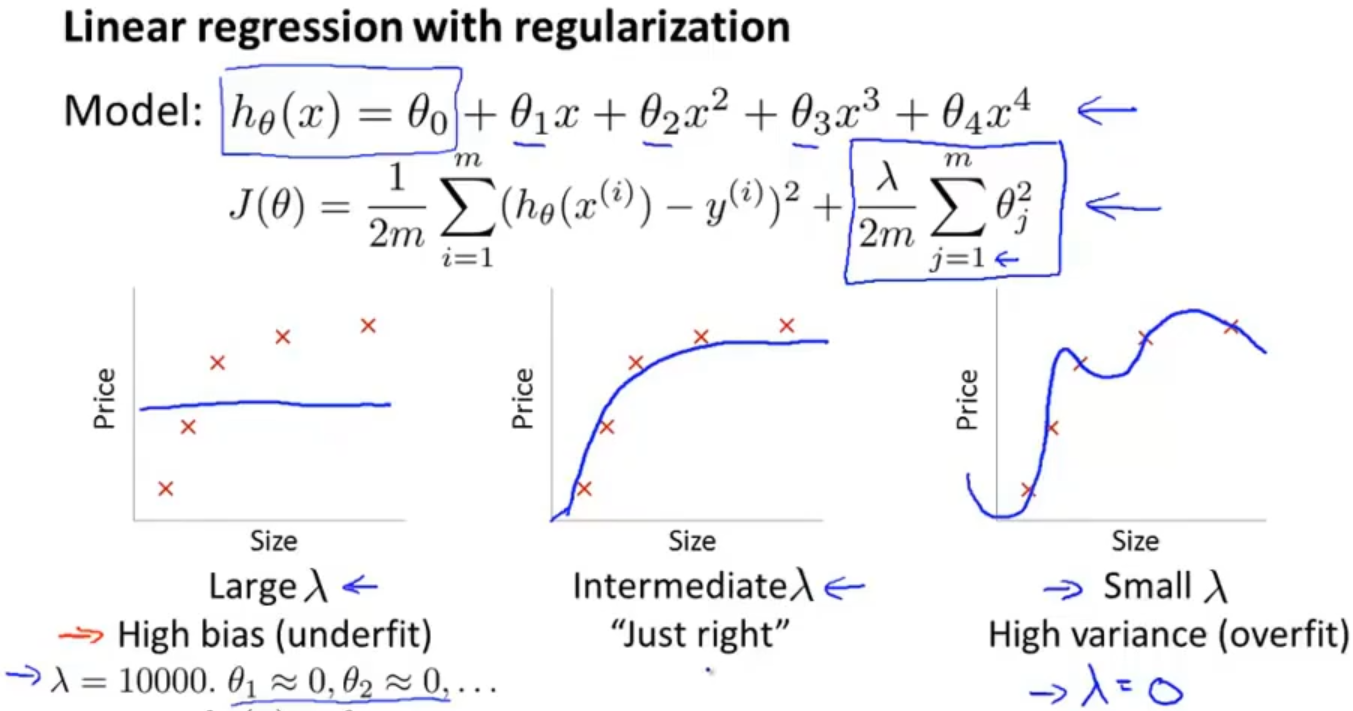
那应该怎么去选择一个合适的λ呢？
首先，把训练集、验证(CV)集、测试集代价函数中的正则项去掉
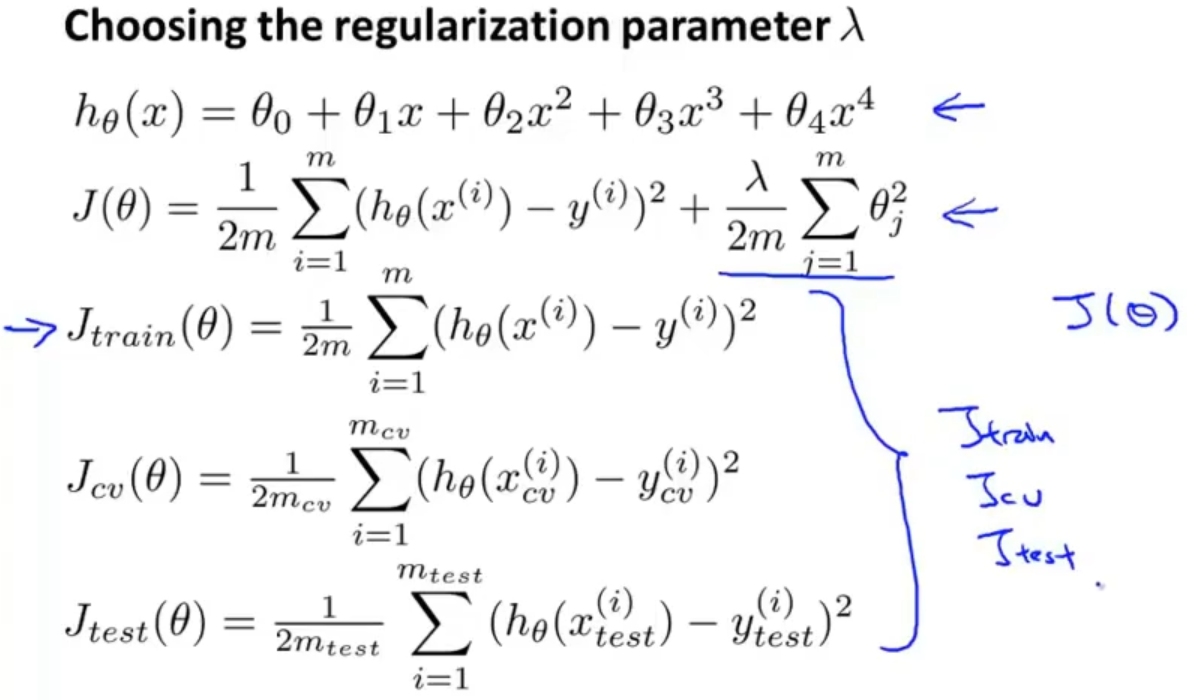
再以2倍步长选择一些备选的参数λ，依次求他们的代价函数最小值，获得参数θ，最后求验证集代价函数Jcv(θ)，选择Jcv(θ)最小的参数λ
假设最小的是Jcv(θ(5))，选择相应的参数θ(5)后，再计算测试集的代价函数
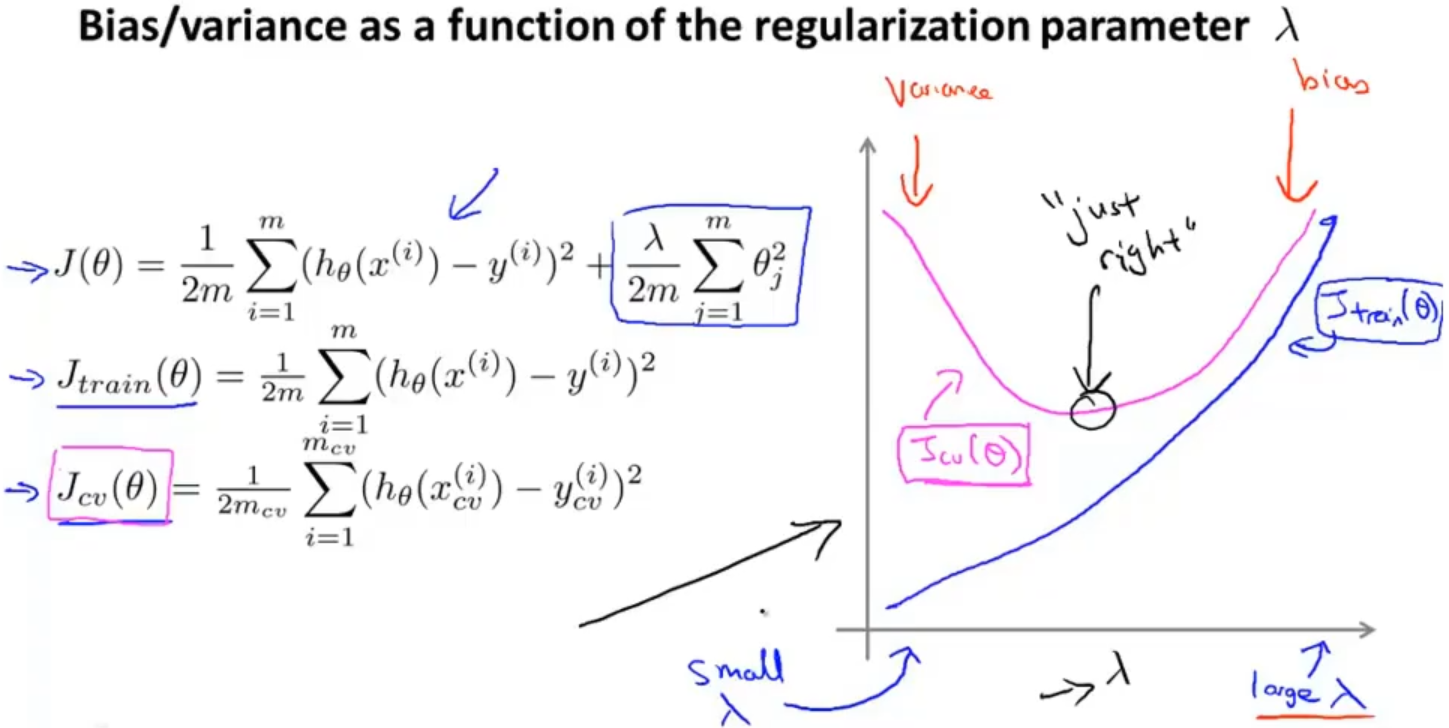
最后来分析一下，λ大小的选取对训练集和验证集的代价函数的影响
当λ比较小的时候，Jcv(θ) 比较大， Jtrain(θ)比较小，那就很有可能产生过拟合，所以这一端是高方差区域
当λ比较小的时候，Jcv(θ) 和 Jtrain(θ)都比较大，那就很有可能产生欠拟合，所以这一端是高偏差区域
1.6 学习曲线 Learning curves
我们可以通过学习曲线来判断一个模型是否处于一个高偏差或者是高方差
m为训练集的数量
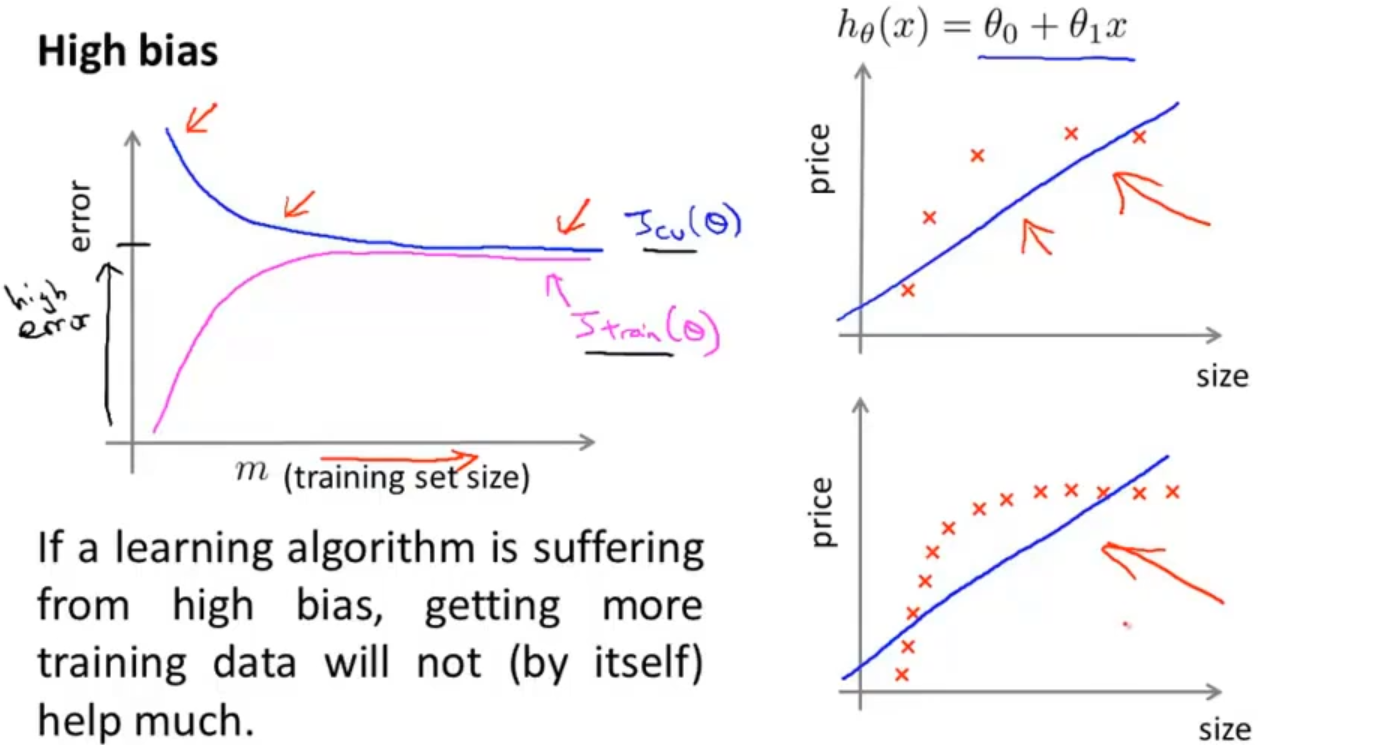
高偏差，欠拟合：随着m的增加，并不能得到什么改善
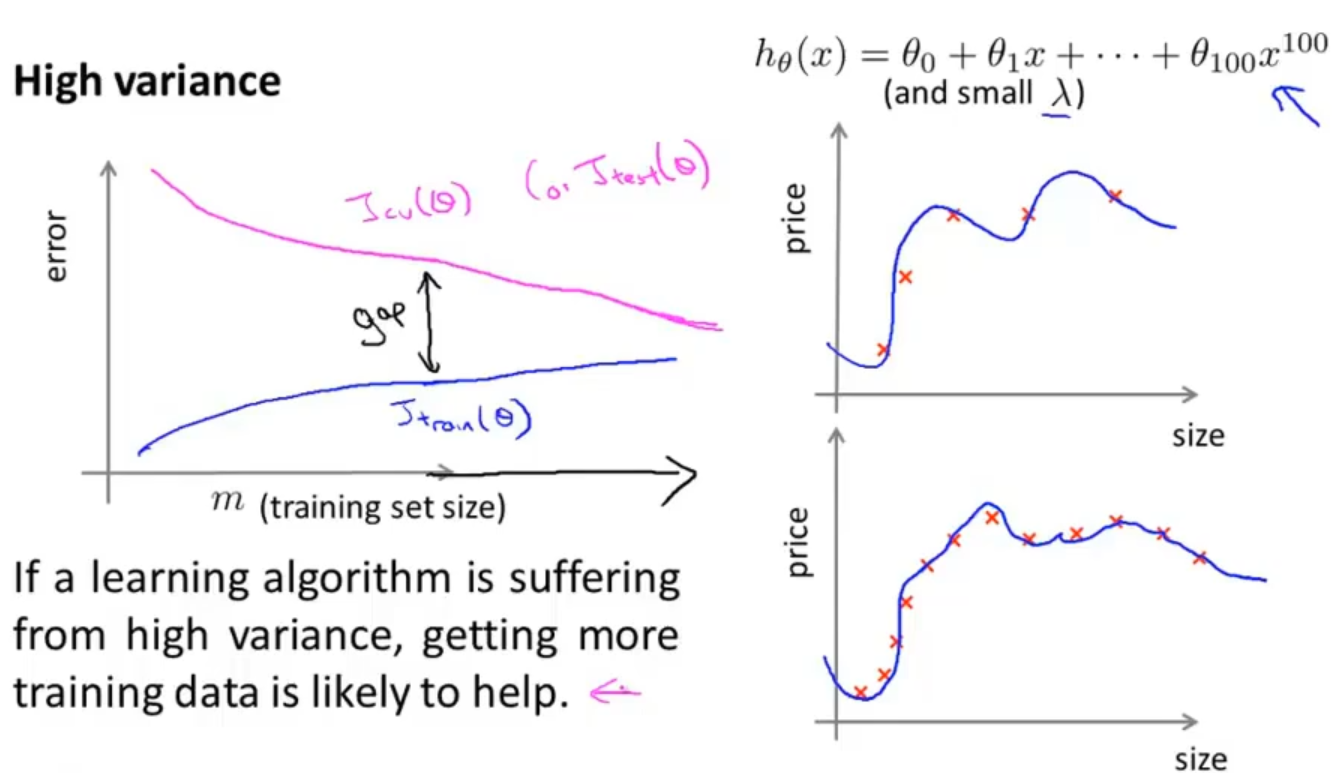
高方差，过拟合：随着m的增加，有可能得到一些改善
那么遇到问题的时候就可以做出相应的解决方法了，回顾之前举的案例：
1、获得更多的训练实例（高方差）
2、尝试减少特征的数量（高方差）
3、尝试获得更多的的特征（高偏差）
4、尝试增加多项式特征（高偏差）
5、尝试减少归一化程度λ（高偏差）
6、尝试增加归一化程度λ（高方差）
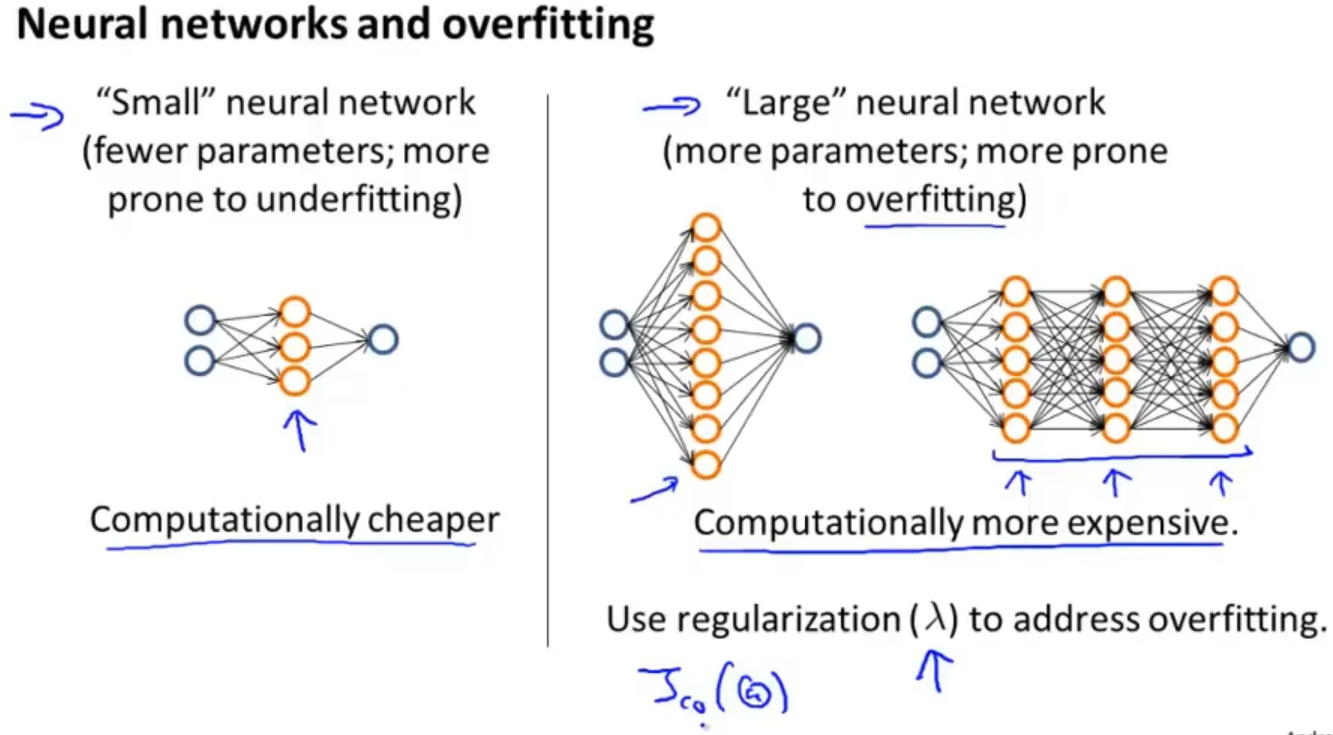
同样的，在神经网络中也会出现类似的问题，如果选择比较简单的网络，虽然计算量比较小但容易出现欠拟合，如果选择比较复杂的网络，计算量比较大而且容易出现过拟合，不过可以使用正则化来修正过拟合
所以在选择模型的时候可以将数据集划分成训练集、验证集和测试集，然后依次对各种层数的神经网络训练，在验证集中选取一个表现最理想的模型作为最后选定的模型
