机器学习笔记7

神经网络学习

1.1 代价函数 Cost function

假设我们神经网络的结构和训练集如下图，我们将用L表示神经网络的层数，s_l表示第l层神经元的个数，在这个例子中L=4，s₁=3，s₂=5，s₄=4

在分类问题上，分成了二分类和多分类问题，二分类的神经网络输出层就只有一个神经元(输出值)，多分类则是有k个(k≥3)

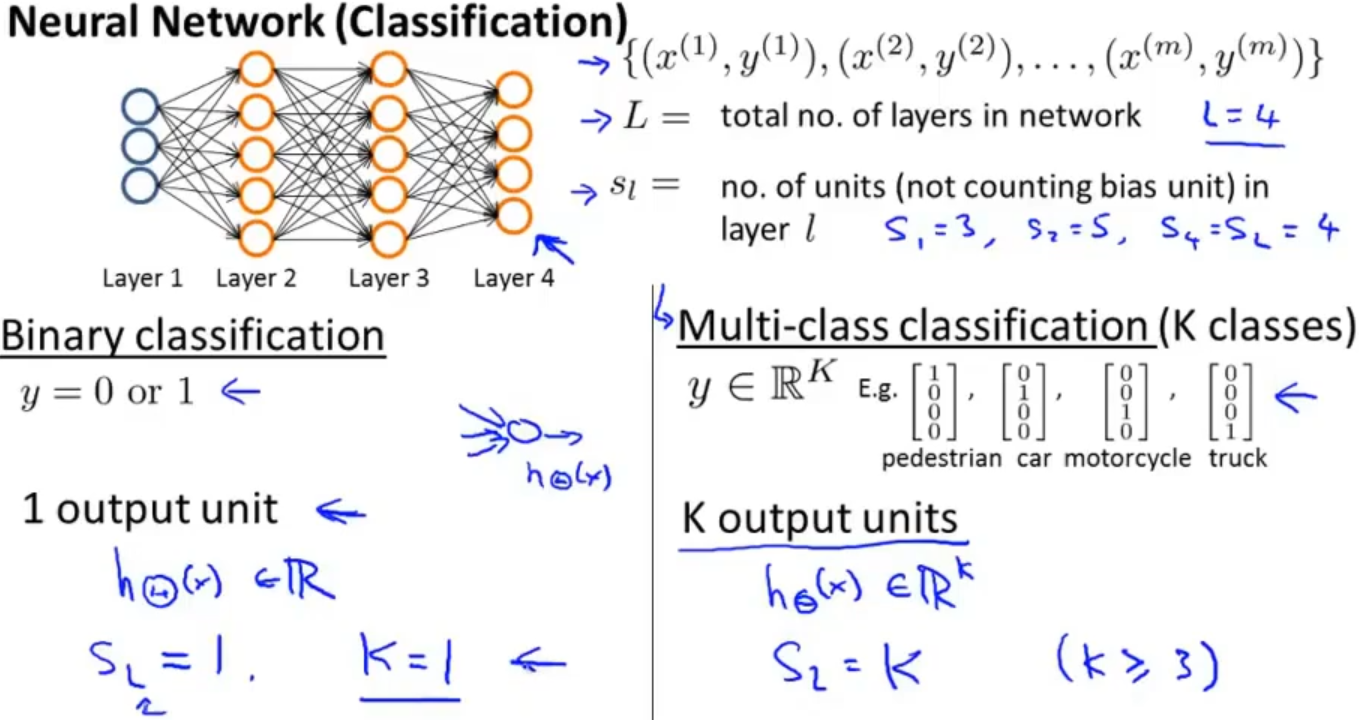
神经网络的代价函数如下图，其实就是逻辑回归代价函数的一般化，h_Θ(x)的维度是K(K表示输出类别个数)，(h_Θ(x))_i表示h_Θ(x)输出的K维向量中的第i个值

由于是K分类，所以代价函数中的表示也相应改变：y_k⁽ⁱ⁾和(h_Θ(x))_k。同时也增加了对k项求和，可以理解为是k类输出都按逻辑回归中代价函数的相应部分计算了一遍，就有k个。正则项也是按照逻辑回归中的原理，还是不对θ₀(偏置项)进行处理

1.2 反向传播算法 Backpropagation algorithm

在梯度的计算过程中，为了最小化J(θ)，需要求出代价函数的偏导项，那我们就需要采用方向传播的方式了

首先我先来看前向传播，我们是需要计算各层的激活项

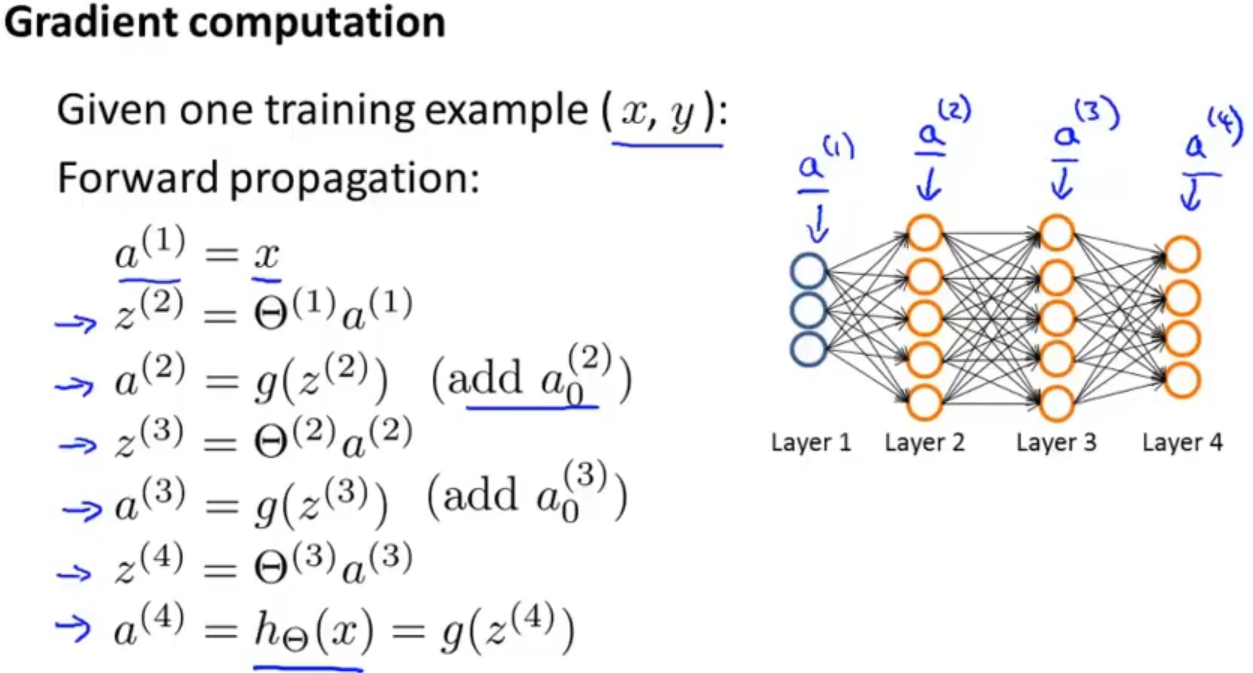
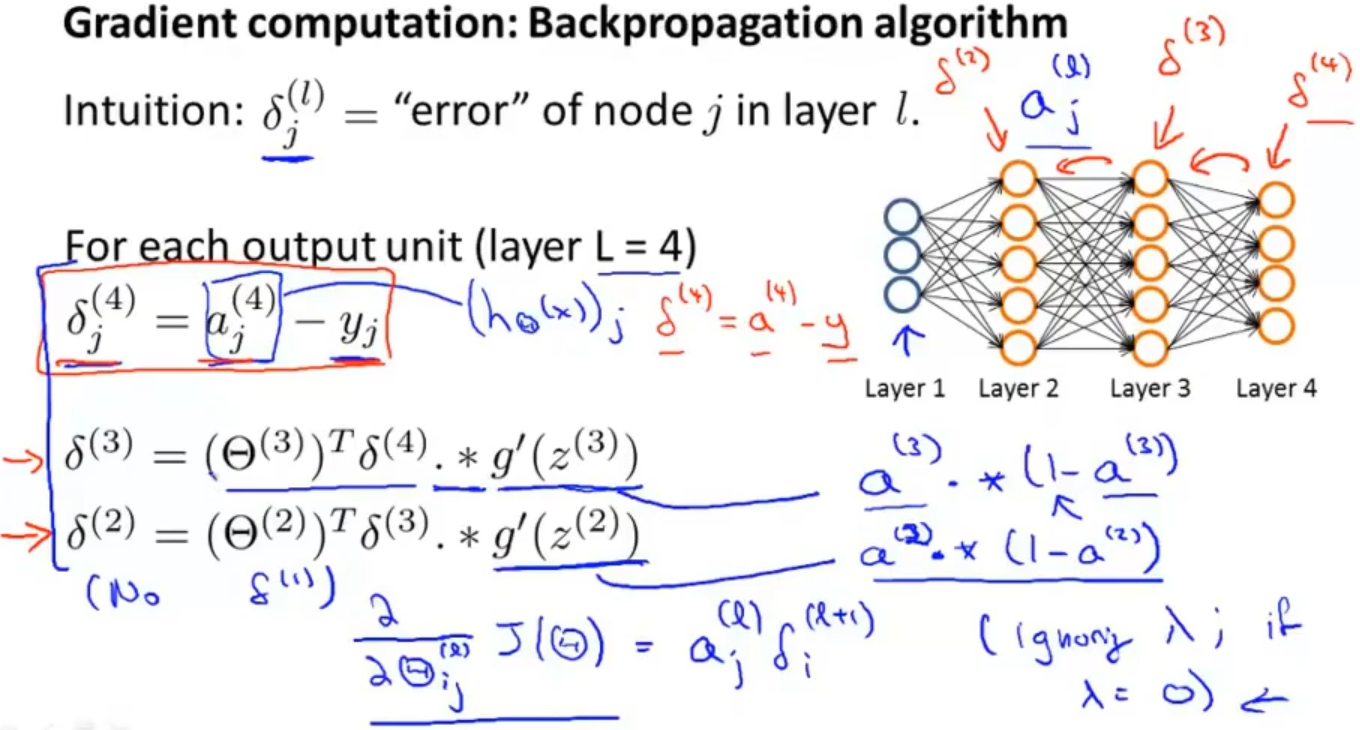
在反向传播中，我们需要计算每一次的误差，当然不包括第一层，因为第一层是我们直接从数据集中输入的，其中 𝛿_j^(l)表示第l层中第j个神经元的误差

从第4层开始，先计算第四层中激活项与真实值的误差 𝛿_j⁽⁴⁾ = 𝑎_j⁽⁴⁾ - 𝑦_j 作为当层激活项的误差，同时也可以把这个进行向量化 𝛿⁽⁴⁾ = 𝑎⁽⁴⁾ - 𝑦

第3层的误差计算：𝛿⁽³⁾ = (𝛩⁽³⁾)^𝑇𝛿⁽⁴⁾ ∗ 𝑔′(𝑧⁽³⁾) ，其中(𝜃⁽³⁾)^𝑇𝛿⁽⁴⁾ 表示权重导致的误差的和， 𝑔′(𝑧⁽³⁾)是 sigmoid函数的导数，sigmoid函数导数有一个特点：𝑔′(𝑧⁽³⁾) = 𝑎⁽³⁾∗(1−𝑎⁽³⁾)

同理第2层误差计算：𝛿⁽²⁾=(𝛩⁽²⁾)^𝑇𝛿⁽³⁾∗𝑔′(𝑧⁽²⁾)

计算好各层的误差后，就可以计算代价函数的偏导数了假设 λ=0(不做正则化的处理)，就有：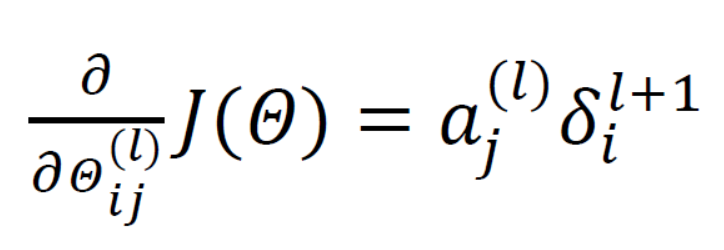

传播的整个过程如下图，最后求得的D_ij^(l)就是代价函数关于每个参数的偏导数，之后就可以使用梯度下降或者其他算法了

1.3 理解反向传播 Backpropagation intuition

现在来理解一下反向传播的过程，首先我们从前向传播开始看，它是一个从前往后依次计算z^(j),a^(j) 的过程

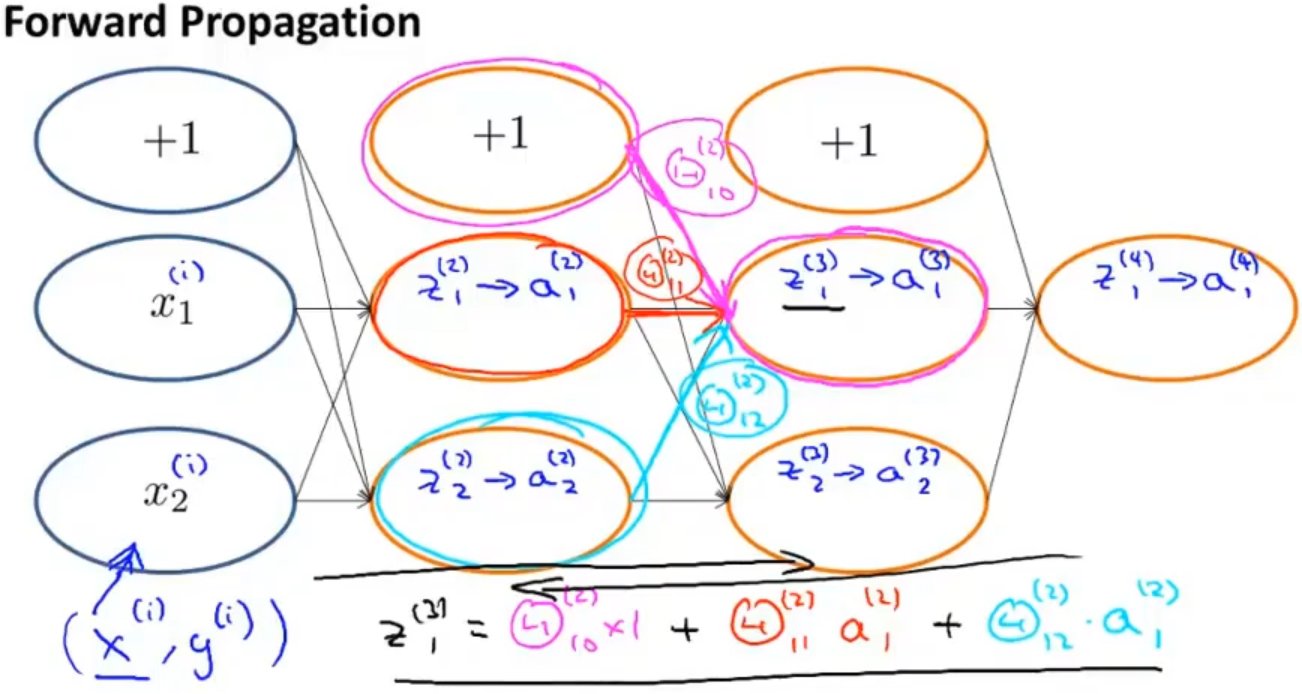
然后对代价函数进行简化，取消掉正则项(λ=0)，得到代价函数cost(i)

反向传播的思想与前向传播类似，先计算出最后一层的误差𝛿₁⁽⁴⁾ ，依次从后往前计算各层激活项的误差，比如𝛿₂⁽³⁾ =𝛩₁₂⁽³⁾∗𝛿₁⁽⁴⁾，𝛿₂⁽²⁾ =𝛩₁₂⁽²⁾∗𝛿₁⁽³⁾+𝛩₂₂⁽²⁾∗𝛿₂⁽³⁾

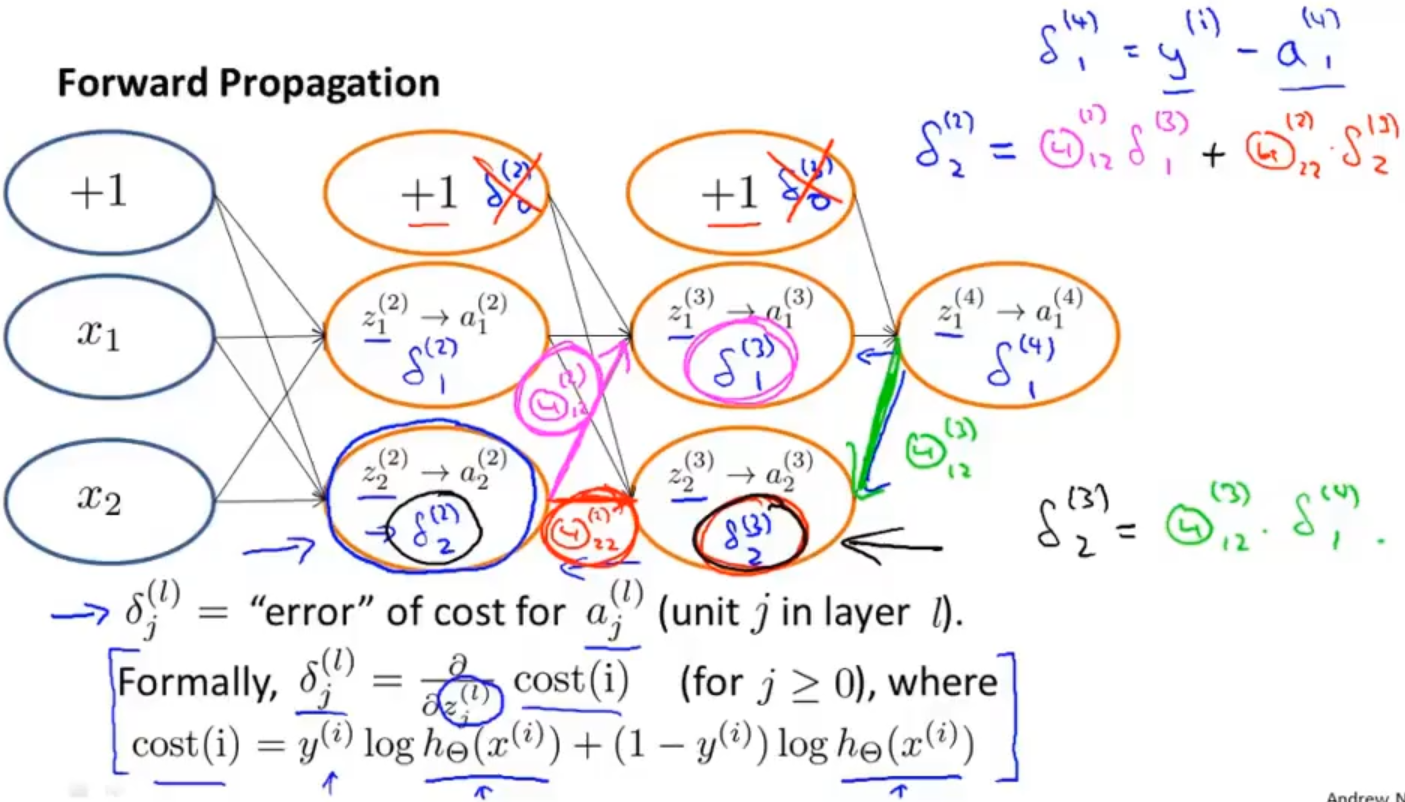
1.4 使用注意：展开参数 Implementation note：Unrolling parameter

在使用Octave时，需要优化权重矩阵，这个时候就需要将矩阵展开成向量进行优化，优化后再转会成矩阵

举个例子：假设有三层的神经网络，第一层和第二层有十个神经元，第三层有一个神经元，Θ和D的维度定义如下

使用代码演示一下展开矩阵和转回矩阵

代码如下：

定义Theta1，Theta2，Theta3

>> Theta1 = ones(10,11)
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1

>> Theta2 = 2*ones(10,11)
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2

>> Theta3 = 3*ones(1,11)
   3   3   3   3   3   3   3   3   3   3   3

将Theta1，Theta2，Theta3组合在一起并展开转换成一个向量

>> thetaVec = [Theta1(:);Theta2(:);Theta3(:)];
>> size(thetaVec)
   231     1

转回成矩阵

>> reshape(thetaVec(1:110),10,11)
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   1   1   1   1   1   1   1   1
>> reshape(thetaVec(111:220),10,11)
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
   2   2   2   2   2   2   2   2   2   2   2
>> reshape(thetaVec(221:231),1,11)
   3   3   3   3   3   3   3   3   3   3   3

1.5 梯度检测 Gradient checking

当你在做前向传播和反向传播的时候往往是需要去做梯度检测的，这样可以检查你的前向传播和反向传播是否出现差错

那我们是通过什么样的方式检测呢？

假设反向传播最后得到参数为θ，它的导数为 d( J(θ) ) / dθ，我们在θ的两侧寻找一个下ε，分别是 (θ-ε) 和 (θ+ε)，计算 [ J(θ+ε)-J(θ-ε) ] / 2ε 的值，检查该值是否近似于 d( J(θ) ) / dθ

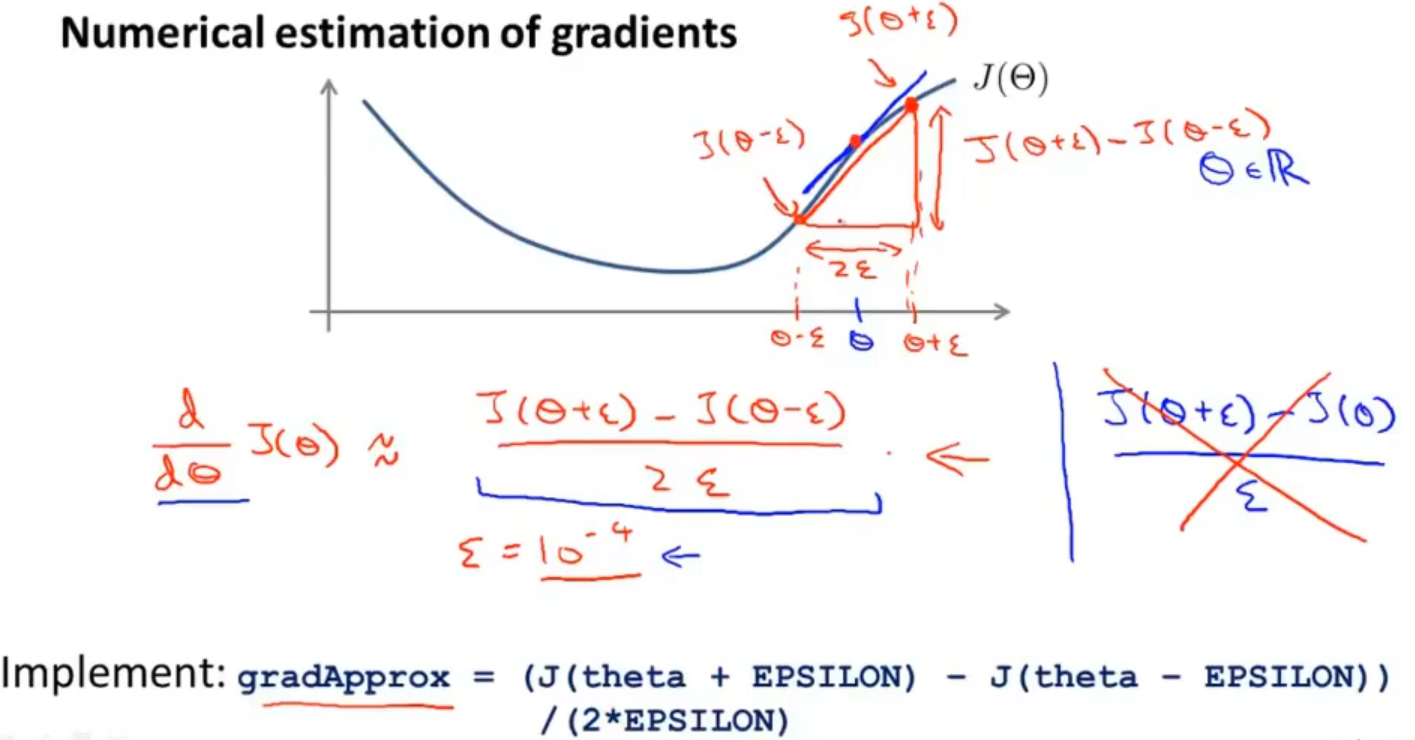
对于向量Θ，则是依次对每个相应的θ_i做类似的计算

在Octave中，相应的代码实现如下

总结一下整个过程，首先先计算出反向传播得到的导数值，然后进行梯度检查，确保它们是近似相等的，最后需要注意的是，在使用代码进行学习或训练神经网络之前需要关闭梯度检查，因为它每次迭代都进行梯度检查的话，它会使你的程序变得非常的慢

1.6 随机初始化 Random initialization

对于参数的初始化问题，在逻辑回归中一般把参数初始化为0，但在神经网络中把参数初始化为0似乎并起不到作用

以下面这个神经网络为例，如果我们把所有权重都初始化为0的话，那就意味着激活项a₁⁽²⁾和a₂⁽²⁾相同，包括后面计算误差值、对代价函数的偏导和迭代后的激活项都相同，这样就以为整个神经网络中几乎所有的东西都是相同的，那么这个神经网络就学习不到任何东西，所以我们就认为在神经网络中把参数初始化为0并不是一个对的选择

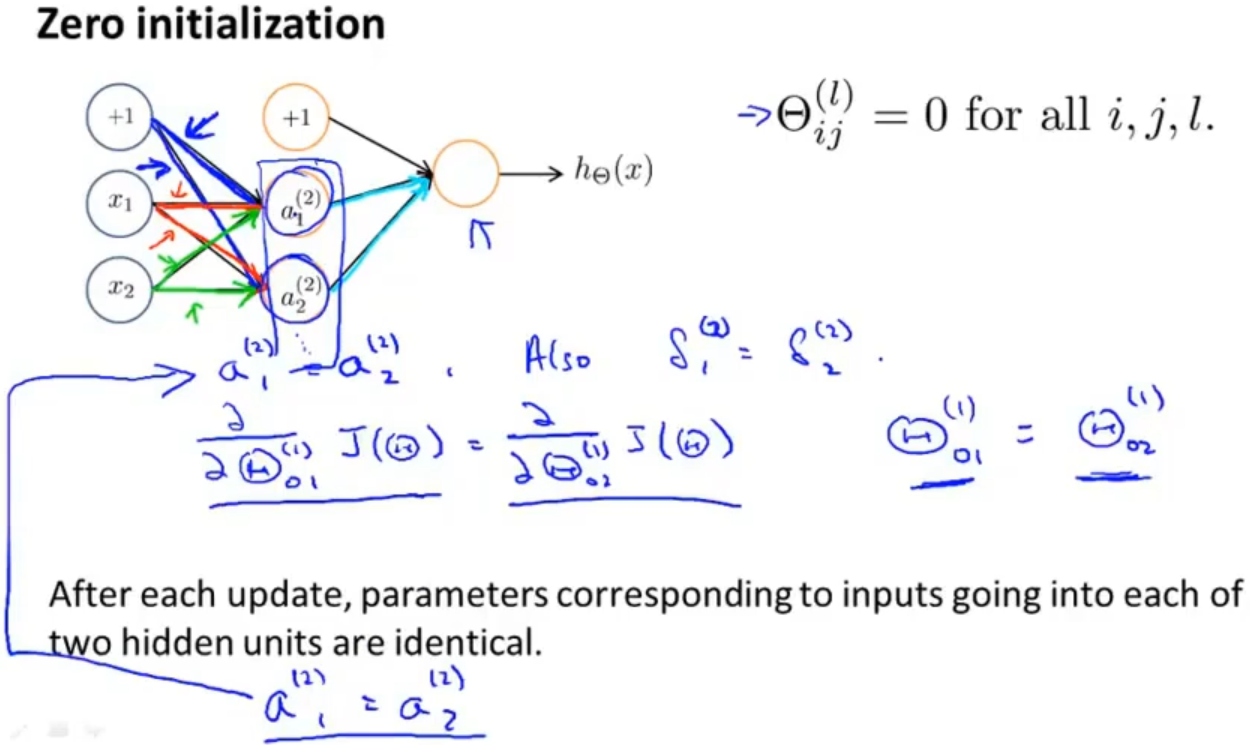
所以就推出了随机初始化的方法，让参数相应的矩阵生成0到1之间的随机数再乘以两倍的ε后减去ε，这样就可以生成-ε到ε之间的随机数了(这里提到的ε与梯度检查中的ε没有关系)

1.7 组合到一起 Putting it together

最后将整理一下搭建神经网络的整个过程

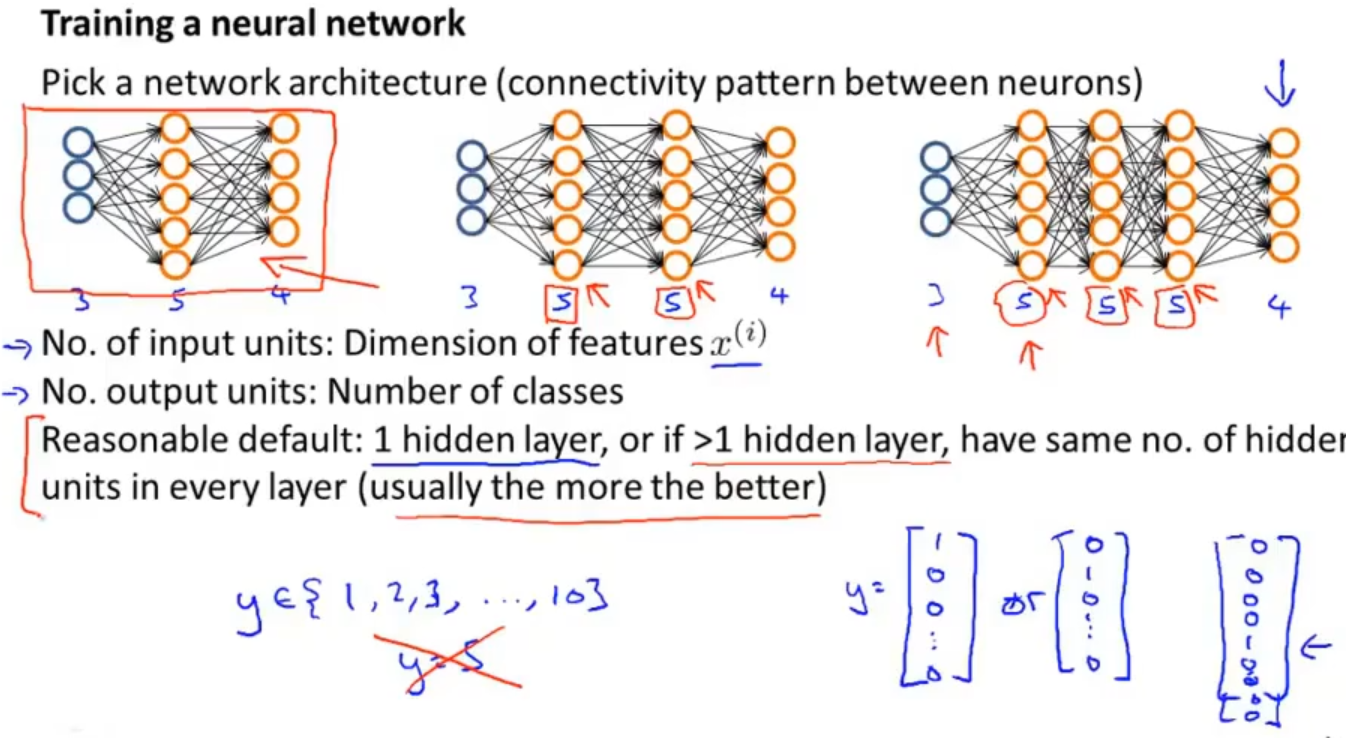
首先，我们需要根据实际问题选择一个合适的神经网络模型，输入和输出层有几个神经元，有多少层隐藏层，都需要根据特征的维度来选择的

同时不要忘了将输出值转成向量的形式

然后需要对权重参数进行随机初始化，进行前向传播获得输出值，再计算代价函数J(Θ)，最后实现反向传播求得偏导数，在进行前向传播和反向传播时需要对整个数据集的每一个样本进行遍历计算

之后需要进行梯度检查，检查之后可以采用梯度下降或者别的高级算法进行优化最小化代价函数J(Θ)来获得最优的参数Θ

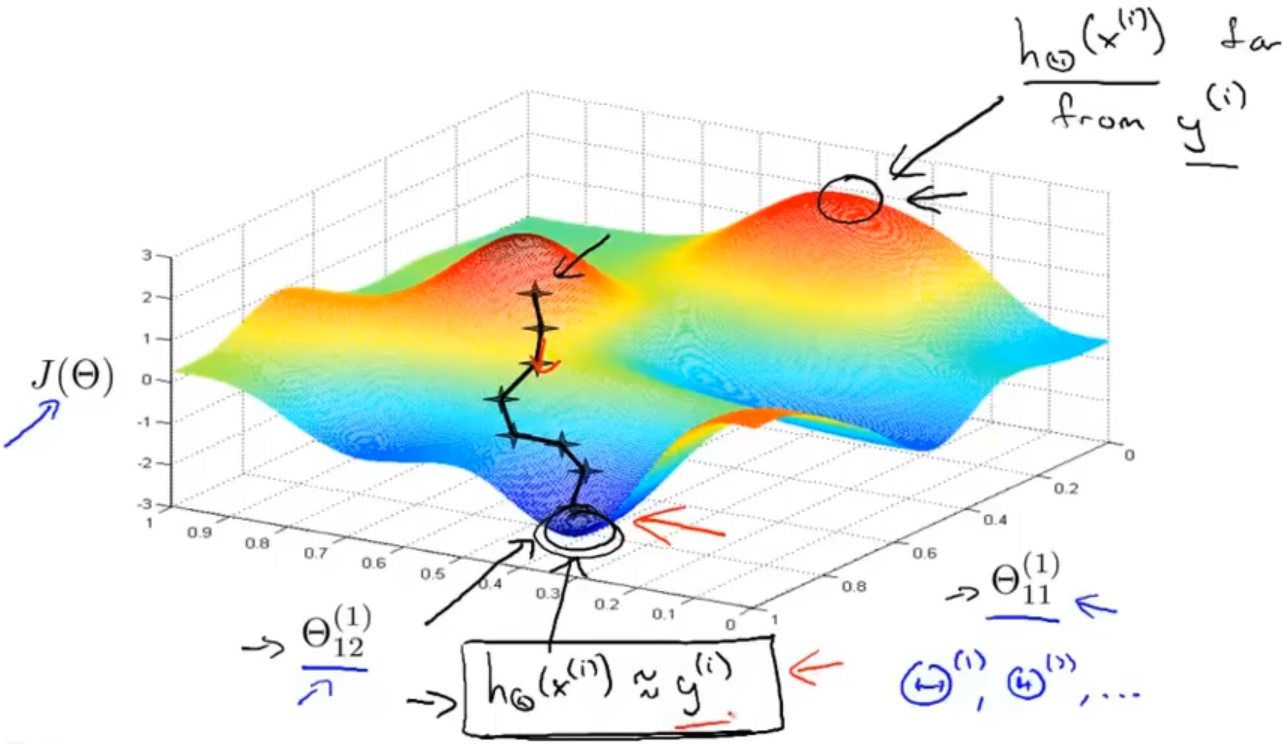
最后以一个图来更直观的理解梯度下降算法