机器学习笔记2
单变量线性回归 Linear regression with one variable
1.1 模型表示 Model Representation
1.1.1 线性回归
学习第一个监督学习的算法:线性回归,其中只有一个参数的线性回归算法称为:单变量线性回归
首先来看一个根据房屋大小预测价格的例子

线性回归中的数据表示:

下面符号定义分别为:
m:代表训练集中实例的数量
x:代表特征/输入变量
y:代表目标变量/输出变量
(x,y):代表训练集中的实例
(x(i),y(i)):代表第i个实例
1.1.2 单变量线性回归
线性回归模式表示:
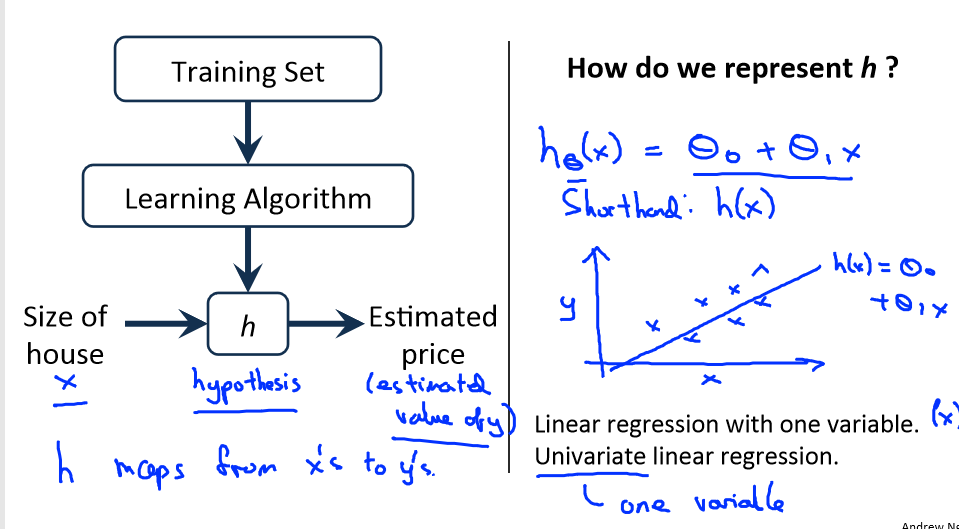
h:代表学习算法的解决方案或函数也称为假设(hypothesis)
h根据输入的x值来得出y值,y值对应房子的价格。如果将y关于x的函数表示为: ,那么就可以把这个问题叫成单变量线性回归问题
,那么就可以把这个问题叫成单变量线性回归问题
1.2 代价函数 Cost Function
代价函数可以理解为是优化目标函数

比如有m=47个样本,假设函数h为 ,我们需要做的就是优化假设函数h即选择适合的参数θ0 和 θ1 ,使得误差最小
,我们需要做的就是优化假设函数h即选择适合的参数θ0 和 θ1 ,使得误差最小
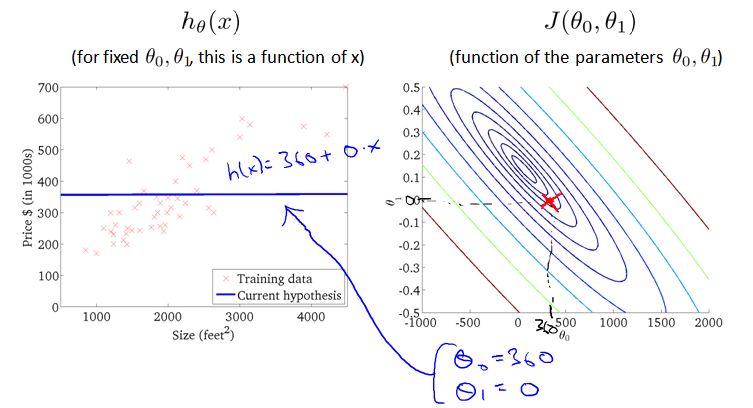
选取不同的参数 θ0 和 θ1,产生的 h 不同,最终的直线也不同:
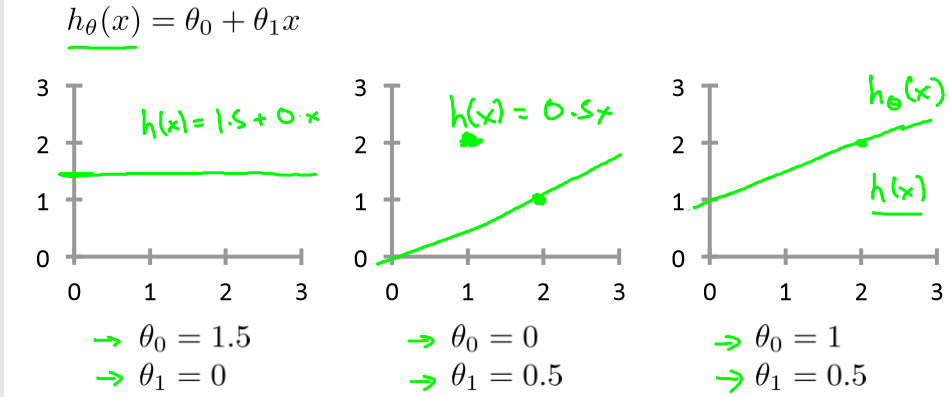
我们需要找到一个最合适的参数来接近真实值,也就是求目标函数的最优解。等价于求下面J函数的最小值


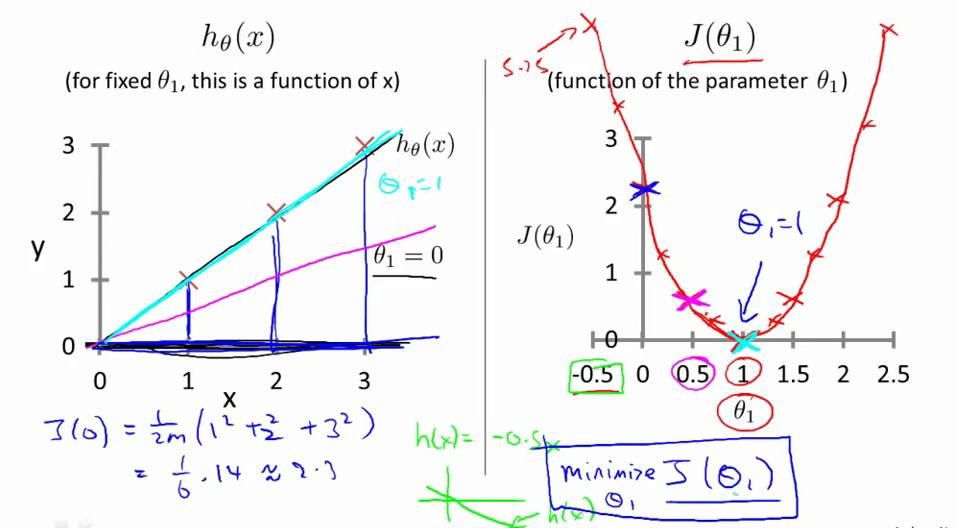
举个例子:
有数据点(1,1),(2,2),(3,3),设θ0=0,即函数h(x)过原点,左图中从上到下的三条直线分别是θ1=1,0.5,0,右图为代价函数J(θ1)
在右图中,很明显当θ1=1时,为代价函数J(θ1)取得最小值,是我们优化的目标
当同时考虑θ0 和 θ1 时是代价函数J(θ1)则转为三维图像
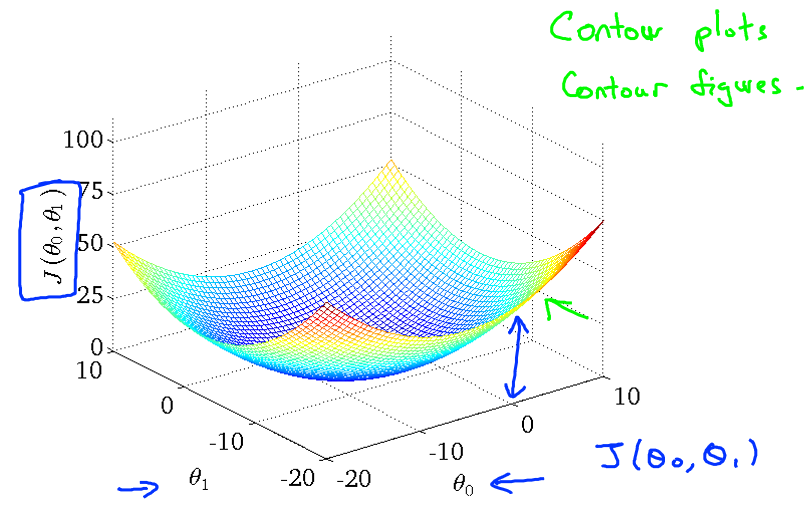
也可以将三维图像转为等高线图(轮廓图),与h(x)一起观测优化过程


1.3 梯度下降 Gradient descent
1.3.1 梯度下降简介
梯度下降法是让代价函数J得到最优化
假设只有θ0 和 θ1,不断的更新θ0 和 θ1的值,直到最优解,当然也有可能是局部最优

可以想象成我们一开始在山顶,每次迈出一步都是最快下山的方向,不断的下降高度,直到到达最低点


1.3.2 梯度下降算法
梯度下降算法对 θ赋值, 使得 J(θ)按梯度下降最快方向进行, 一直迭代下去, 最终得到局部最小值,即收敛 convergence
梯度下降算法不只用于线性回归, 可以用来最小化任何代价函数 J。公式如下

求导的目的,基本上可以说取这个红点的切线,即这条红色直线。由于曲线右侧斜率为正,导数为正。 因此,θ1 减去一个正数乘以 α,值变小。
曲线左侧斜率为负,导数为负。 因此,θ1 减去一个负数乘以 α,值变大。
