高等数学学习笔记- 复杂的极限问题:洛必达法则,等价无穷小,泰勒展开

高等数学学习笔记- 复杂的极限问题

目录

• 高等数学学习笔记- 复杂的极限问题
  • 关于极限的总结
  • 洛必达法则的应用
    • 分式型:0/0与∞/∞型
    • 做差型:∞-∞型
    • 乘积型:0×±∞型
    • 指数型:1^±∞,00,∞^0型
  • 无穷小理论
    • 无穷小的概念
    • 常见等价无穷小
    • 等价无穷小在极限乘除法中的使用
    • 等价无穷小在极限加减法中的运用
    • 基于泰勒展开的等价无穷小

关于极限的总结

• 首先尝试直接将\(x\)替换为\(a\)，用连续性
• 一些代数变换技巧:分式分离常数，根式有理化，对数和差转化为乘积，去绝对值
• 如果还是未定式，考虑洛必达。若形式复杂，可以用等价无穷小代换简化。碰到指对三角混合，可尝试泰勒展开。(后两种直接洛计算量大)
• 尝试分离出常见函数的极限

洛必达法则的应用

分式型:0/0与∞/∞型

首先检查该分式是否0/0或∞/∞,然后才可使用洛必达法则(否则会错),注意导函数之比的极限要么可以直接求出值、要么是未定式(继续使用洛必达)

\[\lim_{x \to a}\frac{f(x)}{g(x)}=\lim_{x \to a}\frac{f'(x)}{g'(x)} \]

在洛必达法则的过程中，还要注意及时分离出极限已知的式子，如把\(\sin x/x\)直接变成1, 以免式子过于复杂难以求导

做差型:∞-∞型

通分、或同时乘以共轭表达式,转成分式型

\[\lim_{x \to 0}(\frac{1}{x}-\frac{1}{\sin x})=\lim_{x \to 0}\frac{x-\sin x}{x\sin x}=\lim_{x \to 0}\frac{1-\cos x}{\sin x+x\cos x}=\lim_{x \to 0}\frac{\sin x}{2\cos x-x\sin x}=0 \]

常见的共轭表达式\(\sqrt{a}-\sqrt{b}\)与\(\sqrt{a}+\sqrt{b}\)

乘积型:0×±∞型

把其中一个取倒数,转成分式型。注意尽量选简单的取倒数，便于求导。

如\(\lim_{x \to 0}x\ln x=\lim_{x \to 0}\frac{\ln x}{1/x}=\lim_{x \to 0}{1/x}{-1/x^2}=\lim_{x \to 0}-x=0\)

这是转化为∞/∞的分式型

指数型:1^±∞,00,∞^0型

取对数,转化为乘积型,再变回指数

如\(\lim_{x \to 0} (\sqrt{1+x^2}+x)^{1/x}=\lim_{x \to 0}\exp(\frac{1}{x}\ln(\sqrt{1+x^2}+x))=\exp(\lim_{x \to 0}\frac{\ln(\sqrt{1+x^2}+x)}{x})=e^1=1\) (洛必达过程略)

无穷小理论

无穷小的概念

如果\(\lim_{x \to x_0}f(x)=0\),那么称\(f(x)\)是\(x \to x_0\)的无穷小。(\(x_0\)换成\(\pm\infin\))同理.

无穷小就是一个极限为0的函数(或数列).注意\(0\)也是无穷小,且是可以成为无穷小的唯一实数。
当自变量\(x\)趋于相同值时，无穷小也可以看成一个量参与运算，常用字母\(\alpha,\beta..\)。等表示(自变量 \(x\)不写出)

无穷小与极限的关系:在\(x\)的同一变化过程中，\(f(x)\)具有极限\(A\)的充要条件是\(f(x)=A+\alpha\),其中\(\alpha\)是无穷小

无穷小量都趋于0，但有些趋于零的速度更快

若 \(\alpha,\beta\)是无穷小量\(\alpha \neq 0\)

\(\lim_{x \to a}\frac{\beta}{\alpha}=0\)则称\(\beta\)为\(\alpha\)的高阶无穷小,记为\(\beta=o(\alpha)\) (注意这里的定义很容易理解反,可以考虑\(x \to 0,\beta=x^3,\alpha=x^2\)的情况来记忆,\(\beta\)趋于0的”速度“更”快“,所以极限为0)

\(\lim_{x \to a}\frac{\beta}{\alpha}=c\neq 0\)则称\(\beta\)为\(\alpha\)的同阶无穷小。若\(c=1\),则称\(\beta\)为\(\alpha\)的等价无穷小，记作\(\alpha\sim \beta\)

\(\lim_{x \to a}\frac{\beta}{\alpha}=\infin\)则称\(\beta\)为\(\alpha\)的低阶无穷小

常见等价无穷小

以下的公式的前提是: \(x \rightarrow 0\); 其它的极限过程只需要做变换:\(x \rightarrow a, x-a \rightarrow 0 ; x \rightarrow \infty, \frac{1}{x} \rightarrow 0\)

\[x \sim e^{x}-1 ; x \ln a \sim a^{x}-1 \]

\[x \sim \ln (1+x) ; \frac{x}{\ln a} \sim \log _{a}(1+x) \]

\[x \sim \sin x \sim \tan x \sim \arcsin x \sim \arctan x \]

\[\frac{1}{2} x^{2} \sim (1-\cos x) \]

\[\lambda x \sim(1+x)^{\lambda}-1 \]

根据泰勒展开还可以推出更多的等价无穷小

在极限求解中，我们可以把某个表达式替换为其等价无穷小来简化极限计算(如把超越函数变成幂函数)。但是并不是任何时候都可以替换的(见下文)

注意:

1. 等价无穷小不是相等,而是近似
2. 等价性不唯一
3. 等价性具有传递性 \(a\sim b,b\sim c\),则\(a\sim c\)
4. 等价无穷小中的\(x\)只是一个形式变量,可以整体代换:若\(\alpha(x)\sim \beta(x)(x \to 0)\),\(\lim_{x \to 0}f(x)=0,则\alpha(f(x))\sim\beta(f(x))\)

等价无穷小在极限乘除法中的使用

　等价无穷小在乘除法中使用, 当且仅当这个等价无穷小”在待求极限的整个式子中表现为“可以提出的整体乘法(或除法)因式”

如\(\lim_{x \to 0}\frac{1-\cos x}{x\sin x}=\frac{1/2x^2}{x\cdot x}=\frac{1}{2}\), ( \(\sin x\) 可以作为因式单独提出来)

相反,如\(\lim_{x \to 0}(\frac{\ln(1+x)}{x^2}-\frac{1}{x})\)就不能用\(\ln(1+x)\)的等价无穷小替代

这是我个人对该规则的理解:这里的等价无穷小替换相当于用了极限的四则运算法则

把上面的规则用数学语言表达(相当于把\(\alpha(x)\)整体提出来)。

\[\alpha(x)\sim\beta(x),\lim_{x \to 0}\alpha(x)f(x)=\lim_{x \to 0} \beta(x)f(x) \]

由等价无穷小的定义\(\lim_{x \to 0}\frac{\alpha(x)}{\beta(x)}=1\),故

\[\lim_{x \to 0}\alpha(x)f(x)=\lim_{x \to 0}(\frac{\alpha(x)}{\beta(x)}\beta(x)f(x))=\lim_{x \to 0}(\frac{\alpha(x)}{\beta(x)})\cdot \lim_{x \to 0} \beta(x)f(x)=1\cdot\lim_{x \to 0} \beta(x)f(x) \]

等价无穷小在极限加减法中的运用

考虑极限\(\lim_{x \to 0}\frac{x-\sin x}{x^3}\),能否把\(x\)换成\(\sin x\)而求出极限为0? 这显然是错误的，由洛必达法则\(\lim_{x \to 0}\frac{x-\sin x}{x^3}=\lim_{x \to 0}\frac{1-\cos x}{3x^2}=\frac{\sin x}{6x}=1/6\)

为什么会出现问题?

我们把 \(\sin x\) 展开到第三项, \(\sin x=x-\frac{x^3}{6}+o(x^3)\) ,其中\(o(x^3)\)表示任何比\(x^3\)高阶的项,如\(x^a(a>3)\)

代入原式得:

\[\lim_{x \to 0}\frac{x-(x-\frac{x^3}{6}+o(x^3))}{x^3}=\frac{1}{6}+\lim_{x \to 0}\frac{o(x^3)}{x^3}=\frac{1}{6} \]

其中\(o(x^3)\)表示一个比无穷小量\(x^3\)高阶的无穷小量，根据定义\(\lim_{x \to 0}\frac{o(x^3)}{x}=0\)

相反,用\(\sin x \sim x\)相当于只展开到第一项,即\(\sin x=x+o(x)\),那么结果就变成了\(\lim_{x \to 0}\frac{o(x)}{x^3}\),因为\(o(x)\)可能是\(x^2,x^3,x^4....\),极限的值无法确定。

实际上,高阶无穷小有以下运算规则:
当 \(x \rightarrow 0\) 时 :

1. \(o\left(x^{n}\right) \pm o\left(x^{n}\right)=o\left(x^{n}\right)\) (同阶加减，阶数不变)

2. 当 \(m>n\) 时， \(o\left(x^{m}\right) \pm o\left(x^{n}\right)=o\left(x^{n}\right)\) (不同次加减，取次数低)

3. \(o\left(x^{m}\right) \cdot o\left(x^{n}\right)=o\left(x^{m+n}\right), x^{m} \cdot o\left(x^{n}\right)=o\left(x^{m+n}\right)\)

4. 设 \(\varphi(x)\) 有界， \(\varphi(x) \cdot o\left(x^{n}\right)=o\left(x^{n}\right)\)

5. 注意,\(o(x^n)-o(x^n) \neq 0\), \(\frac{o(x^m)}{o(x^n)} \neq o(x^{m-n})\)

6. \(\lim_{x \to 0}\frac{o(x^n)}{x^n}=0\)

基于泰勒展开的等价无穷小

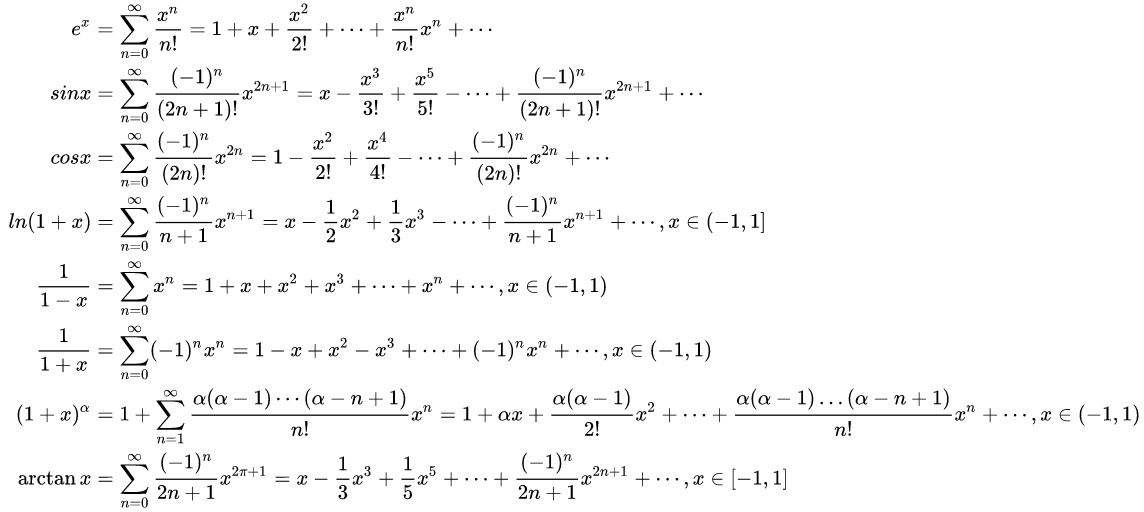
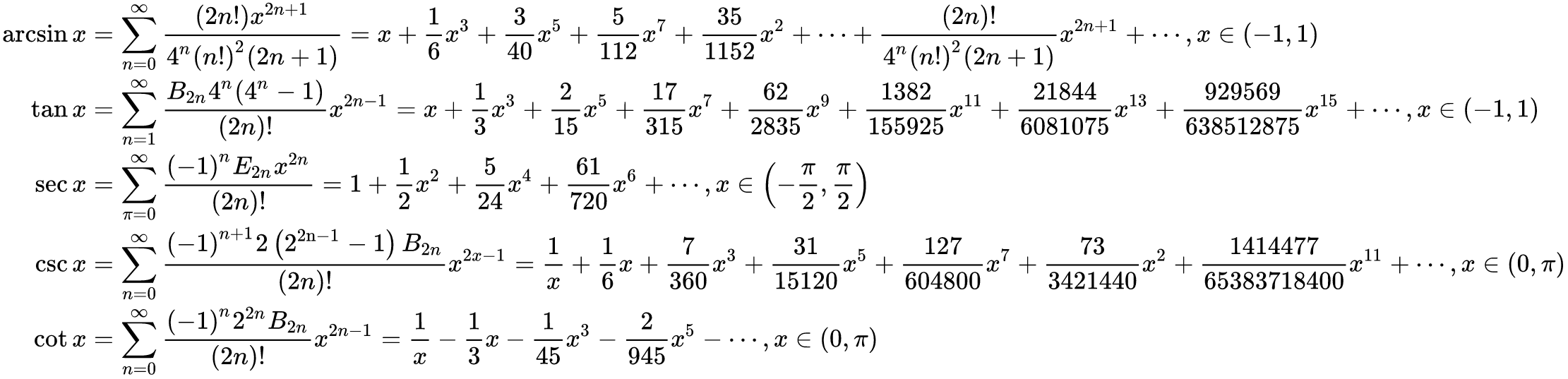
那么要展开到几项?
如果是乘除法，上下必须要同阶。就如同\(\frac{x-\sin x}{x^3}\)这个例子.如果是分母和分子中的加减法,我们希望展开到运算后首个不为0的项,否则仍然是未定式。因此,只要找到正确的展开项数,并替换(带上 \(o(x^n)\) ,避免出错)

实际上，若\(f\)有最低次项(系数不为0)\(a_nx^n\)的麦克劳林级数,那么\(x \to 0\)时\(f(x)\sim a_nx^n\), 运用该结论就可以得到常见等价无穷小中的一系列式子

除了这些外，比较常用的还有:

\[\sqrt{1+x}=1+\frac{1}{2}x^2+o(x) \]

例:求

\[\lim_{x \to 0} \frac{e^x-1-\sin x}{\sin x(e^x-1)} \]

\[e^x-1=x+\frac{x^2}{2}+\frac{x^3}{6}+\dots \]

\[\sin x=x-\frac{x^3}{6}+\dots \]

容易看出\(x^2\)是第一个非零项,展开到第二项那么 \(e^x-1-\sin x=\frac{x^2}{2}+o(x^2)\). 于是原极限为

\[\lim_{x \to 0}\frac{\frac{x^2}{2}+o(x^2)}{\sin x(e^x-1)}=\lim_{x \to 0}\frac{\frac{x^2}{2}+o(x^2)}{x^2}=\frac{1}{2} \]

(注意对分母用到了乘除法的等价无穷小替换)