再探快速傅里叶变换(FFT)(其四) 多项式操作

再探快速傅里叶变换(其四) 多项式操作

省选前夕爆补一波多项式全家桶,存一些板子

再探快速傅里叶变换(其四) 多项式操作

多项式乘法

不解释。注意如果式子太复杂，直接全部DFT再按原式子算,最后IDFT。这里封装好是为了简化模板代码,而且可以方便的换成任意模数NTT

void poly_mul(ll *a,ll *b,ll *c,int n,int m){
    static ll ta[maxn+5],tb[maxn+5];
    int N=1,L=0;
    while(N<n+m-1){
        N*=2;
        L++;
    }
    for(int i=0;i<n;i++) ta[i]=a[i];
    for(int i=n;i<N;i++) ta[i]=0;
    for(int i=0;i<m;i++) tb[i]=b[i];
    for(int i=n;i<N;i++) tb[i]=0;
    for(int i=0;i<N;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(ta,N,1);
    NTT(tb,N,1);
    for(int i=0;i<N;i++) c[i]=ta[i]*tb[i]%mod;
    NTT(c,N,-1);
    for(int i=n+m-1;i<N;i++) c[i]=0;
}

多项式求逆

定义:LuoguP4238给出$n-1$次多项式$f(x)$,我们要求一个多项式$g(x)$,满足$f(x)g(x) \equiv 1(\bmod \ x^n)$.
系数对NTT模数取模.

求逆的算法基于倍增,是迭代进行的。假设我们已经求出了一个$h(x)$,满足$f(x)h(x) \equiv 1 (\bmod\ x^{\frac{n}{2}})$

由定义有$f(x)g(x) \equiv 1(\bmod\ x^{\frac{n}{2}})$

两式做差,的$h(x)-g(x) \equiv 0 (\bmod x^{\frac{n}{2}})$

平方,得$h^2(x)-2h(x)g(x)+g^2(x) \equiv 0(\bmod\ x^n)$

两边同时乘上$f(x)$,将$f(x)g(x)=1$代入,移项可得:

\[g(x) \equiv h(x)(2-f(x)h(x)) (\bmod\ x^n) \]

因此递归求出$h(x)$后,就可以推出$g(x)$.边界条件$n=1$时$g_0=f_0^{-1}$. 时间复杂度满足递推式$T(n)=T(\frac{n}{2})+n \log n$,根据主定理为$\Theta(n\log n)$

void poly_inv(ll *f,ll *g,int n){
    static ll tmp[maxn+5];
    if(n==1){
        g[0]=inv(f[0]);
        return;
    }
    poly_inv(f,g,(n+1)/2);
    poly_mul(f,g,tmp,n,n);
    poly_mul(tmp,g,tmp,n,n);
    for(int i=0;i<n;i++) g[i]=(2*g[i]-tmp[i]+mod)%mod; 
}

多项式取余

定义:[LuoguP4512]给定一个$n$次多项式$f(x)$和一个$m$次多项式$g(x)$,求两个多项式$q(x),r(x)$.满足$f(x)=q(x)g(x)+r(x)$,且$q(x)$次数为$n-m$,$r(x)$次数小于$m$.模数为NTT模数。

我们先定义一种操作$r$,若$f(x)=\sum_{i=0}^{n}a_ix^i$,则$f_r(x)=\sum_{i=0}^{n-1}a_ix^{n-i}$.实际上就是把系数顺序倒过来。容易发现$f_r(x)=x^nf(\frac{1}{x})$.接下来开始推式子

\[\begin{aligned} f(x)=q(x) \cdot g(x)+r(x) \\ \Leftrightarrow f\left(\frac{1}{x}\right)=q\left(\frac{1}{x}\right) \cdot g\left(\frac{1}{x}\right)+r\left(\frac{1}{x}\right) \\ \Leftrightarrow x^{n} f\left(\frac{1}{x}\right)=x^{n-m} q\left(\frac{1}{x}\right) \cdot x^{m} g\left(\frac{1}{x}\right)+x^{n-m+1} \cdot x^{m-1} r\left(\frac{1}{x}\right) \\ \Leftrightarrow f_{r}(x)=q_{r}(x) \cdot g_{r}(x)+x^{n-m+1} \cdot r_{r}(x) \\ \Leftrightarrow f_{r}(x) \equiv q_{r}(x) \cdot g_{r}(x) \quad\left(\bmod x^{n-m+1}\right) \\ \Leftrightarrow q_{r}(x) \equiv f_{r}(x) \cdot g_{r}^{-1}(x) \quad\left(\bmod x^{n-m+1}\right) \end{aligned}\]

我们只需要在$\bmod\ x^{n-m+1}$下对$g_r$求逆,就能求出$q_r$和$q$,然后用$r(x)=f(x)-g(x)q(x)$求出$r$.

//a就是f,b就是g
void poly_mod(ll *a,ll *b,ll *q,ll *r,int n,int m){
    static ll ra[maxn+5],rb[maxn+5],invrb[maxn+5];
    for(int i=0;i<n;i++) ra[i]=a[i];
    for(int i=0;i<m;i++) rb[i]=b[i];
    reverse(ra,ra+n);
    reverse(rb,rb+m);
    for(int i=n-m+1;i<n*2;i++) rb[i]=0;
    poly_inv(rb,invrb,n-m+1); //在mod x^(n-m+1)下做 
    poly_mul(ra,invrb,q,n,n-m+1);
    for(int i=n-m+1;i<n*2;i++) q[i]=0;
    reverse(q,q+n-m+1);
    poly_mul(q,b,r,n-m+1,m);
    for(int i=0;i<n;i++) r[i]=(a[i]-r[i]+mod)%mod;
}

多项式ln

定义:LuoguP4725给出$n-1$次多项式$f(x)$,我们要求一个多项式$g(x)$,满足$g(x) \equiv \ln f(x)(\bmod \ x^n)$.
系数对NTT模数取模.保证常数项为1.

对上式求导,$g'(x)=[\ln f(x)]'=\ln'(f(x))\cdot f'(x)=\frac{f'(x)}{f(x)}$

这样就可以用多项式求逆得到$g'(x)$,再积分回去就好了。
保证常数项为1,是保证原多项式为整系数的情况下,$\ln$多项式的常数用整数算得出来.并且我们发现求导的过程中实际上把常数项忽略掉了。

void poly_deriv(ll *f,ll *g,int n){
    for(int i=1;i<n;i++) g[i-1]=f[i]*i%mod;
    g[n-1]=0;
} 
void poly_inter(ll *f,ll *g,int n){
    for(int i=n-1;i>=1;i--) g[i]=f[i-1]*inv(i)%mod;
    g[0]=0;
}
void poly_ln(ll *f,ll *g,int n){
    static ll invf[maxn+5];
    poly_deriv(f,g,n);
    poly_inv(f,invf,n);
    poly_mul(g,invf,g,n,n);
    poly_inter(g,g,n*2);
    for(int i=n;i<n*2;i++) g[i]=0;
}

多项式exp

泰勒展开

泰勒展开是用多项式来逼近指数函数,三角函数等函数。因为转化成了多项式函数,所以很多时候能简化分析(比如在生成函数问题中)。

为了逼近(感性理解就是让图像形状更接近)目标函数$f(x)$,我们先选点$(x_0,f(x_0))$来切入,让多项式函数$g(x)$经过这一点。为了让图像更接近,我们让此处的增减性相同(一阶导数相同),凹凸性相同(二阶导数相同),以及更高阶的导数相同...

实际操作中我们不用无限阶求导,只需算到$n$阶.

设$g(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\dots a_n(x-x_0)^n$.(每一项里面的$x-x_0$是为了保证过定点)

由初始点相等,有$a_0=f(0)$
由$x_0$处$n$阶导数相等,有$f^{(n)}(x_0)=g^{(n)}(x_0)=n!a_n$,即$a_n=\frac{f^{(n)}}{n!}$.(求$n$阶导之后只有第$n$项留下来,$a_nx^n \rArr na_nx^{n-1} \rArr n(n-1)a_nx^{n-2} \rArr \dots n!a_n$)

代入,得

\[g(x)=f(0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dots \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) \]

这就是著名的泰勒展开式.其中$R_n(x)$是佩亚诺(Peano)余项,感性理解就是和真实值的误差。特别地,令$x_0=0$就可以得到麦克劳林展开:

\[g(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\dots \frac{f^{(n)}(0)}{n!}x^n+R_n(x) \]

现在给出一些OI中常用函数的泰勒展开。在生成函数问题中经常用到.

\[e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\dots \frac{x^n}{n!}+\dots=\sum_{n=0}^{\infin}\frac{x^n}{n!} \tag{1} \]

证明:取$x_0=0$,$e^x$求导等于本身,所以每一项都是$e^0=1$

\[\frac{1}{1-x}=1+x+x^2+x^3+\dots=\sum_{n=0}^{\infin} x^n \tag{2} \]

证明:取$x_0=0$,$(\frac{1}{1-x})'=\frac{1}{(1-x)^2},\frac{1}{(1-x)^2}'=\frac{1}{2!(1-x)^3}\dots$

\[-\ln (1-x) =\frac{x}{1}+\frac{x^2}{2}+\dots \frac{x^n}{n}+\dots=\sum_{n=1}^{\infin} \frac{x^n}{n} \tag{3} \]

证明: 对上式两边求导,即可得到$(2)$

牛顿迭代

牛顿迭代是一种求方程近似解的方法。

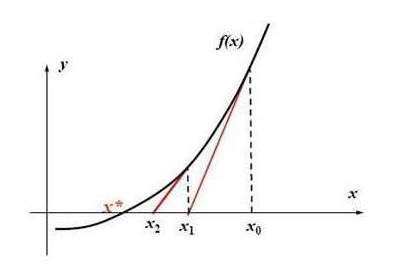
牛顿迭代的几何解释如图,先选取一个初始值$x_0$,向上做垂线与$f(x)$的图像相交。作$f(x)$在$x_0$处的切线交$x$轴于$x_1$,从$x_1$再向上做垂线,如此迭代,$x_i$会逐渐趋近于方程的解。由导数的几何意义,$x_i$处切线方程为$y=f'(x_i)x+f(x_i)-f'(x_i)x_i$.令$y=0$,得交点坐标$x_{i+1}=x_{i}-\frac{f(x_i)}{f'(x_i)}$. 按照这个递推式不断迭代就可以得到近似解。

其中迭代的实数$x_i$也可以换成一个多项式,并且在模意义下进行。

假设我们已经求出$h(x)$满足$f(h(x)) \equiv 0(\bmod\ x^{\frac{n}{2}})$,要求$f(g(x)) \equiv 0(\bmod\ x^n)$

此时就可以求出模意义下的精确解。把$f(g(x))$在$h(x)$处泰勒展开,有:

\[f(g(x))=f(h(x))+f'(h(x))(g(x)-h(x)+\frac{f''(h(x))}{2!}(g(x)-h(x))^2+\dots \]

因为我们是迭代进行的,显然有$g(x)\equiv h(x) (\bmod\ x^{\frac{n}{2}})$.那么对于$\forall i \geq 2$有$(g(x)-h(x))^i \equiv 0(\bmod\ x^n)$,也就是说
$f(g(x))=f(h(x))+f'(h(x))(g(x)-h(x))$,移项得

\[g(x)=h(x)-\frac{f(h(x))}{f'(h(x))}(\bmod\ x^n) \]

exp的求解

定义:LuoguP4726给出$n-1$次多项式$f(x)$,我们要求一个多项式$g(x)$,满足$g(x) \equiv \mathrm{e}^{f(x)} (\bmod\ x^n)$.
系数对NTT模数取模

对上式两边求$\ln$,得$\ln(g(x))-f(x) \equiv 0(\bmod\ x^n)$

令$H(t(x))=\ln(t(x))-f(x)$,把$t(x)$看成自变量,用牛顿迭代求使得$H(t(x))=0$的$t(x)$

我们设第$i$次迭代后的根为$g_i(x)$,根据牛顿迭代的公式有:

\[g_{i+1}(x)=g_{i}(x)-\frac{H(g_{i}(x))}{H'(g_{i}(x))}=g_{i}(x)-\frac{\ln(g_{i}(x))-f(x)}{\frac{1}{g_i(x)}}=g_{i}(x)(1+f(x)-\ln g_{i}(x)) \]

注意$H'(g_{i}(x))=\frac{1}{g_{i}(x)}$,因为我们把$g_{i}(x)$看作自变量,$f(x)$看作常数。

每次迭代都使得精度翻倍(指的是最高次翻倍).复杂度$T(n)=T(\frac{n}{2})+n\log_2n$,即$\Theta(n\log n)$

void poly_exp(ll *f,ll *g,int n){
    static ll lng[maxn+5];
    if(n==1){
        g[0]=1;
        return;
    }
    poly_exp(f,g,(n+1)/2);
    poly_ln(g,lng,n);
    for(int i=0;i<n;i++) lng[i]=(f[i]-lng[i]+mod)%mod;
    lng[0]++;
    poly_mul(g,lng,g,n,n);
    for(int i=n;i<n*2;i++) g[i]=0;
}

多项式开根

二次剩余

定义:对于正整数$p,n$,若存在$x$使得$x^2 \equiv n(\bmod\ p)$.则称$n$是模$p$的二次剩余。(在本文中我们只考虑$p$为奇质数的情况)

勒让德括号,欧拉判别准则

下面引入勒让德括号,它可以简化讨论:

\[\left(\frac{n}{p}\right)=\left\{\begin{array}{ll}1 & (p \nmid n \text { 且 } n \text { 是模 } p \text { 的二次剩余 }) \\ -1 & (p \nmid n \text { 且 } n \text { 是模 } p \text { 的二次非剩余 }) \\ 0 & (p \mid n)\end{array}\right. \]

上面的$-1$在模意义下其实就是$p-1$

定理(欧拉判别准则): 当$p$为奇素数时,$\left( \frac{n}{p}\right) \equiv n^{\frac{p-1}{2}} (\bmod\ p)$

证明: $p|n$的情况是显然的,我们考虑$p \nmid n$时的情况。显然$n^{\frac{p-1}{2}}=\plusmn 1$.若$n$是二次剩余,则$n^{\frac{p-1}{2}}=(x^2)^{\frac{p-1}{2}}=x^{p-1}=1$. 若$n^{\frac{p-1}{2}}=1$,把$n$用模$p$下的原根$g$表示为$n=g^k$,那么$g^{k\frac{p-1}{2}}=1$.又因为$g^{p-1}=1$,由原根的性质(见此处定理3.1)得到$p-1|k\frac{p-1}{2}$,那么$k$必定为偶数,令$x=g^{\frac{k}{2}}$即可,说明$n$是二次剩余。也就是说 $n^{\frac{p-1}{2}}=1$是$n$是二次剩余的充要条件。反之-1的情况成立。

从这个定理我们已经得到二次剩余的一种求法,求出原根$g$后用BSGS求出$g^k=n$的解,那么$g^{\frac{k}{2}}$就是一个解。复杂度$O(\sqrt{p})$

Cipolla算法

上面这个$O(\sqrt{p})$的算法还不够优秀,我们用Cipolla算法来求解$x^2 \equiv n(\bmod\ p)$。算法流程如下:

不断随机$a$,直到找到一个$a$使得$a^2-n$是非二次剩余(用欧拉判别准则判断)(我们之后会证明期望随机次数为2).
定义$\omega^2=a^2-n$.但是我们知道$a^2-n$是非二次剩余,那么我们可以类比复数域对无法开根的数$-1$定义$\mathrm{i}^2=-1$,我们把所有数表示为$p+q\omega$的形式,运算规则类似复数。那么$x=\plusmn (a+\omega)^{\frac{p+1}{2}}$.

引理1:$x^2 \equiv n(\bmod\ p)$有且仅有两组解,且满足$x_1+x_2 \equiv n(\bmod\ 0)$

证明:假设对于$x_1 \neq x_2$有$x_1^2 \equiv x_2^2$,移项得$(x_1-x_2)(x_1+x_2)\equiv 0$。这很类似实数的开根。又因为每个$n$都对应两个不同的$x_1,x_2$,一共只有$p-1$个数,那么二次剩余的数量恰为$\frac{p-1}{2}$.那么随机到非二次剩余的概率为$\frac{p-1}{2p} \approx \frac{1}{2}$.期望次数为$\sum_{i=0}\frac{i}{2^i}=2-\frac{N+2}{2^N}$,趋近于2. 这样算法的复杂度就是$O(\log p)$

引理2:$ \omega^{p} \equiv-\omega$
证明： $\omega^{p} \equiv \omega\left(\omega^{2}\right)^{\frac{p-1}{2}} \equiv \omega\left(a^{2}-n\right)^{\frac{p-1}{2}} \equiv-\omega$

引理3:$(A+B)^{p} \equiv A^{p}+B^{p}$
证明：根据二项式定理,由于$p$是质数，除了$C_{p}^{0}, C_{p}^{p}$ 外的組合数分子上的阶乘没法消掉$p$，模$p$都为$0,$ 只有$C_{p}^{0} A^{0} B^{p}+C_{p}^{p} A^{p} B^{0}$

根据引理2,3:

\[(a+i)^{p+1} \equiv\left(a^{p}+i^{p}\right)(a+i)\equiv\left(a\cdot a^{p-1}+i^{p}\right)(a+i) \equiv(a-i)(a+i) \equiv a^{2}-i^{2} \equiv n \]

那么$x=\plusmn (a+i)^{\frac{p+1}{2}}$(可以用反证法证明虚部为0,这里不再赘述)

struct com { //cipolla用的类似复数的东西
    ll real;
    ll imag;//a+b*sqrt(w)
    com() {

    }
    com(ll _real,ll _imag) {
        real=_real;
        imag=_imag;
    }
};
inline com mul(com a,com b,ll w) {//重载乘法
    return com((a.real*b.real%mod+a.imag*b.imag%mod*w%mod)%mod,(a.real*b.imag%mod+a.imag*b.real%mod)%mod);
}
inline com fpow(com x,ll k,ll w) {
    com ans=com(1,0);
    while(k) {
        if(k&1) ans=mul(ans,x,w);
        x=mul(x,x,w);
        k>>=1;
    }
    return ans;
}
inline ll cipolla(ll x) {
    if(fast_pow(x,(mod-1)/2)==mod-1) return -1;//x不存在二次剩余
    while(1) {
        ll a=((rand()<<15)|rand())%mod;
        ll w=(a*a%mod-x+mod)%mod;
        if(fast_pow(w,(mod-1)/2)==mod-1) { //x-a^2不存在二次剩余
            return fpow(com(a,1),(mod+1)/2,w).real%mod;
        }
    }
    return -1;
}

开根求解

定义: LuoguP5277给定一个 $n-1$ 次多项式 $f(x),$ 求一个在 $\bmod x^{n}$ 意义下的多项式 $g(x),$ 使得 $g^{2}(x) \equiv f(x)$ $\left(\bmod x^{n}\right),$ 答案取正的 $\sqrt{f(x)}$(正的指模意义下常数项较小的).NTT模数

多项式开根一般用倍增算法。虽然可以类似求逆直接用定义推式子,但是牛顿迭代更快。另外类似多项式快速幂用$\ln+\exp$也可以,但常数较大.

定义$B(h(x))=h^2(x)-f(x)$,我们要求使得$B(g(x))=0$的$g(x)$.根据牛顿迭代的式子,假设我们已经在模$x^{\frac{n}{2}}$的意义下求出了解$h(x)$,那么有:

\[g(x)=h(x)-\frac{B(h(x))}{B'(h(x))}=h(x)-\frac{h^2(x)-f(x)}{2h(x)}=\frac{h^2(x)+f(x)}{2h(x)} \]

套求逆的板子即可。初始值$g(0)$需要求$f(0)$的二次剩余解,记得取系数小的.

void poly_sqrt(ll *f,ll *g,int n) {
    static ll invg[maxn+5];
    if(n==1) {
        ll root=(Cipolla::cipolla(f[0])%mod+mod)%mod;
        g[0]=min(root,mod-root);
        return;
    }
    poly_sqrt(f,g,(n+1)/2);
    poly_inv(g,invg,n);
    poly_mul(f,invg,invg,n,n);
    ll inv2=inv(2);
    for(int i=0; i<n; i++) g[i]=(g[i]+invg[i])%mod*inv2%mod;
}

多项式快速幂

保证常数项为1

定义:LuoguP5245给出$n-1$次多项式$f(x)$和正整数$k$,我们要求一个多项式$g(x)$,满足$g(x) \equiv f^k(x) (\bmod\ x^n)$.保证常数项为1
系数对NTT模数取模,$n \leq 10^5,k \leq 10^{10^5}$

显然有$f^k(x)=\exp(k \ln f(x)) $(常数项为1是为了求$\ln$)。套前面的板子,复杂度$O(n\log n)$ 注意$k$很大需要取模,因为我们一直在对系数进行操作所以取模的是$p$而不是$p-1$.(这里和费马小定理没有关系!)

void fast_pow(ll *a,ll *b,ll k,int n){
    static ll lna[maxn+5];
    poly_ln(a,lna,n);
    for(int i=0;i<n;i++) lna[i]=lna[i]*k%mod; 
    poly_exp(lna,b,n);//不能直接带入a,否则会破坏初始值
}

不保证常数项为1

定义:LuoguP5273给出$n-1$次多项式$f(x)$和正整数$k$,我们要求一个多项式$g(x)$,满足$g(x) \equiv f^k(x) (\bmod\ x^n)$.不保证常数项为1
系数对NTT模数取模,$n \leq 10^5,k \leq 10^{10^5}$

既然不保证常数项为1,我们可以把常数项除掉。但是常数项也可能为0.那么我们就要找到第一个非0的项,设$f(x)$的最低次项为$ax^d$.那么有:

\[f^{k}(x)=a^{k} x^{k d}\left(\frac{f(x)}{a x^{d}}\right)^{k} \]

对应到系数表达式上,就是把系数先左移$d$位,除以$a$,按普通版的方法求$k$次幂,然后乘上$a^k$,最后再右移$kd$位(如果$kd>n$就直接输出0).注意做多项式$k$次幂和右移$kd$位的时候$k$取模的是$p$,但是求$a^k$的时候$k$取模的是$p-1$.

void fast_pow(ll *a,ll *b,ll k1,ll k2,int n){
    static ll lna[maxn+5];
    ll pos=n;
    for(int i=0;i<n;i++){
        if(a[i]!=0){//找到第一个系数不为0的位置.然后整体左移pos,相当于除法
            pos=i;
            break;
        }
    }  
    if(pos*k1>=n){
        for(int i=0;i<n;i++) printf("0 ");
        return;
    }

    ll d=a[pos];//模板的多项式ln要求常数项a[0]=1,所以要整体除掉常数
    ll invd=inv(d),powd=fast_pow(d,k2);
    for(int i=pos;i<n;i++) a[i-pos]=a[i]*invd%mod; 
    poly_ln(a,lna,n-pos); 
    for(int i=0;i<n-pos;i++) lna[i]=lna[i]*k1%mod; 
    poly_exp(lna,b,n-pos);//不能直接带入a,否则会破坏初始值
    for(ll i=0;i<min(pos*k1,n*1ll);i++) printf("0 ");
    for(ll i=pos*k1;i<n;i++) printf("%lld ",b[i-pos*k1]*powd%mod); //k2在指数上,模mod-1
}

此题细节较多,放上完整代码

多项式多点求值

多项式快速插值

8552ea2d6dad4d8e36cb1ba713e6fbee--clannad-nagisa_waifu2x_art_noise3_scale_tta_1.png

posted @ 2020-07-07 21:13 birchtree 阅读(668) 评论(1) 编辑收藏举报

刷新页面返回顶部

蒟蒻ypy的博客

[已退役][博客迁移到birchtree2.github.io]