图论算法复习笔记
图论算法复习笔记
最短路
最短路算法概述.
| 算法 | 时间复杂度(点数为\(n\),边数为\(m\)) | 限制 |
|---|---|---|
| 堆优化Dijkstra | \(O((n+m)\log m)\) | 正权图 |
| Floyd | \(O(n^3)\) | |
| Bellman-Ford | \(O(nm)\) | 无负环 |
| SPFA | 最坏\(O(nm)\) | 无负环 |
| 拓扑排序 | \(O(n+m)\) | DAG |
最短路树
定义:存在一棵树,使得任意不属于根的节点\(x\),它到根的距离等于原图上从根走到它的最短路。这棵树被称为最短路树。
构建方法:跑Dijkstra的时候若存在\(dist_y>dist_x+w(x,y)\)即"松弛",就把\(y\)的最短路树父亲设为\(x\).注意最短路树不唯一。
[BZOJ1576]安全路径
给出一个n个点m条边的无向图,n个点的编号从1~n,定义源点为1。定义最短路树如下:从源点1经过边集T到任意一点i有且仅有一条路径,且这条路径是整个图1到i的最短路径,边集T构成最短路树。 给出最短路树,求对于除了源点1外的每个点i,求最短路,要求不经过给出的最短路树上的1到i的路径的最后一条边。
先求出最短路树。删掉了树上一个点i到父亲的边(即1到i路径上最后一条边)后,我们必须经过非树边才能到达i。贪心考虑,只经过一条非树边显然是最优的。
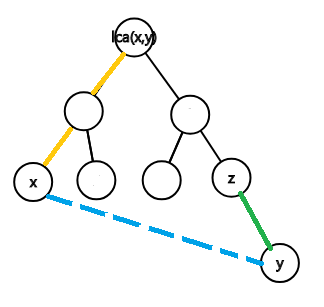
对于一条非树边(x,y) [图中蓝色虚线],它在树上对应一条路径(x,y).对于这条路径上的点z,在z往它父亲的边被删除后,我们可以走这样的路径1->x->y->z。1->x的距离显然为\(dist(x)\),x->y的距离为\(len(x,y)\),y->z的距离[绿线]是\(dist[y]-dist[z]\).因此到z的路径长度就是\(dist[x]+dist[y]+len(x,y)-dist[z]\)。注意到当z=lca(x,y)时,是不能从1->x->y->z的,因为z到父亲的边被删除后无法到达x.
那么方法就很明确了。对于每条边,我们用\(dist[x]+dist[y]+len(x,y)\)去更新路径(x,y)(不包含lca)上的点,每个点\(z\)求出\(min(dist[x]+dist[y]+len(x,y))\)。最后输出\(min(dist[x]+dist[y]+len(x,y))-dist[z]\)即可。路径修改,单点查询,可以用树链剖分解决。时间复杂度\(O(n \log^2 n)\)
最小环
定义:最小环是一个图中由n(\(n \geq 3\)个节点构成的边权和最小的环。
求最小环可以用Floyd算法:
对于无向图,求环的长度就是求两点\(i,j\)加上中间任意一个松弛点\(k\)的距离和.所以可以按照Floyd那样循环。另外要保证\(dist_{i,j}\)经过的点不包含K。 所以枚举\(i,j\)的范围\(<k\),这样由于\(i,j\)的的最短路还没被外层循环更新,保证了正确性。
void floyd(){
for(int k=1;k<=cnt;k++){
for(int i=1;i<k;i++){
for(int j=i+1;j<k;j++){
if(dist[i][j]==INF||edge[i][k]==INF||edge[k][j]==INF) continue;
//防止加法溢出
if(dist[i][j]+edge[i][k]+edge[k][j]<ans){
ans=dist[i][j]+edge[i][k]+edge[k][j];
}
}
}
for(int i=1;i<=cnt;i++){
for(int j=1;j<=cnt;j++){
if(dist[i][j]>dist[i][k]+dist[k][j]){
dist[i][j]=dist[i][k]+dist[k][j];
}
}
}
}
}
给出n个正整数\(a_i\),若\(a_i \& a_j \neq 0\),则连边\((i,j)\)(注意i->j的边和j->i的边看作一条。问连边完图的最小环长度
\(n \leq 10^5,0 \leq a_i \leq 10^{18}\)
我们按位考虑.显然满足第i位为1的所有数两两之间都有边,构成一个完全图.
统计第i位为1的数,如果第i位为1的数超过2个,就直接输出3(这3个构成一个最小环)。如果有2个,就连一条边.注意点的编号要离散化,因为前面可能有很多0,导致满足条件的(i,j)编号很大。因为建图的时候,每一位最多建一条边,边数<64,点数<128,floyd求最小环\(O(n^3)\)可以卡过
实际上,求最小环也可以用Dijkstra枚举源点跑\(n\)次最短路,每次在图上任选两个点和源点求最小环。复杂度\(O(n(n+m)\log n)\).由于常数很大,有时比Floyd要慢。但是可以使得求包含某条边或点的最小环复杂度更优秀。
判负环
负环就是边权和为负的环。
显然如果两点间存在负环,SPFA算法和Bellman-Ford算法会陷入死循环。因为沿着负环一直走距离会越来越小。
在没有负环的情况下,因为一个点最多与n-1个点相连,最多被访问n-1次。所以当某个点被访问到n次时,这条路径上一定有负环。
bool spfa(int s){
dist[s]=0;
inq[s]=1;
cnt[s]++;
q.push(s);
while(!q.empty()){
int x=q.front();
q.pop();
if(cnt[x]>n) return 1;
inq[x]=0;
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(dist[y]>dist[x]+E[i].len){
dist[y]=dist[x]+E[i].len;
if(!inq[y]){
q.push(y);
cnt[y]++;
inq[y]=1;
}
}
}
}
return 0;
}
差分约束系统
如果一个系统由n个变量和m个约束条件组成,形成m个形如\(x_i-x_j≤k\)的不等式(\(i,j∈[1,n],k\)为常数),则称其为差分约束系统(system of difference constraints)。求解差分约束系统,就是找出一组变量x,使得它满足m个约束条件
观察不等式,我们发现它类似于最短路中的不等式\(dist_y \leq dist_x +w(x,y)\)。所以我们可以建图求解这个问题。
首先我们建立一个虚拟源点s,从s向i连边权为0的边,然后对于不等式\(x_i-x_j≤k\),我们连一条j到i的有向边,边权为k.接着跑Bellman-ford或者SPFA求最短路,如果有负环,则无解。否则\(dist_i\)就是一组可行解。具体问题中常出现三种形式的不等关系,建图如下
- \(x_i-x_j \leq k\),建图\((j,i,k)\)
- \(x_i-x_j \geq k\),建图\((i,j,k)\)或\((j,i,-k)\)
- \(x_i-x_j =k\),建图\((i,j,k)\)和\((j,i,k)\)(相当于转化成\(\geq k\)且\(\leq k\))
[HDU 1529]Cashier Employment
有一个超市,在24小时对员工都有一定需求量,表示为\(r_i\),意思为在i这个时间至少要有i个员工,现在有n个员工来应聘,每一个员工开始工作的时间为\(t_i(i \in [0,23])\),并持续8小时,问最少需要多少员工才能达到每一个时刻的需求。前一天16点后的人统计入下一天
答案显然有单调性,可以考虑二分答案mid。对于日夜24小时循环的问题,可以采取把环复制一遍,形成长度为48的链求解。
设\(d_i\)表示前i小时有多少员工开始工作,\(p_i\)表示第i个小时最多可以请来多少员工开始工作,\(r_i\)表示第i个小时需要员工的个数。
限制1:\(d_i -d_{i-8} \geq r_i (i \geq 8)\) 保证第i小时在工作的员工够用
限制2:\(d_i-d_{i-24} =mid\),即24小时中工作的员工恰好等于答案,可以拆成\(d_i-d_{i-24} \geq mid,d_{i-24}-d_i \geq -mid\)
限制3:\(d_i - d_{i-1} \geq 0\),前缀和显然不会下降
限制4:\(d_i - d_{i-1} \leq p_i\),第i个小时在工作的员工不会超过能来的员工数
然后跑差分约束系统,如果无解就增加mid,否则减少mid
k短路
咕咕咕咕~
同余最短路
最小生成树
|算法|时间复杂度(点数为\(n\),边数为\(m\))|
|----|----|----|
|Kruskal| \(O(m\log n)\) |
|Prim | \(O(n^2)\) | |
其中Prim算法在完全图上会比Kruskal优秀
[Codeforces 1245D] Shichikuji and Power Grid
有n个城市,坐标为\((x_i,y_i)\),还有两个系数\(c_i,k_i\).在每个城市建立发电站需要费用\(c_i\).如果不建立发电站,要让城市通电,就需要与有发电站的城市连通。i与j之间连一条无向的边的费用是\((k_i+k_j)\)*两个城市之间的曼哈顿距离.求让每个城市都通电的最小费用,并输出任意一个方案。
把选每个点的代价转成虚拟原点到这个点的边,这个套路很常见,但在最小生成树题里还是第一次见到。
城市之间两两连边,边权按题目里提到的计算。然后建立一个虚拟源点,向每个城市\(i\)连边,边权为\(c_i\).对整个图跑一个最小生成树即可.
次小生成树
非严格次小生成树
Kruskal的本质是贪心,在Kruskal后,\(\forall u,v\)有最小生成树\(u\)和\(v\)间的边权最大值\(\leq\)边\((u,v)\)的权值
因此非严格次小生成树只需要遍历每条未选的边\((u,v,w)\),用它替换最小生成树上点\(u,v\)之间边权最大的边。
求边权最大的边可以用树上倍增维护,
严格次小生成树
为什么之前提到的不严格?因为未选入的边的权值可能等于树上点\(u,v\)之间边权最大值,因此生成树大小不变。那么我们只要再维护一个次大值即可。
[BJWC2010]严格次小生成树
板子题,题面略
最优比率生成树
定义:对于每条边,有花费\(w_i\)和收入\(v_i\),求一个生成树\(T\),最小化\(\sum_{i \in T} \frac{v_i}{w_i}\)
容易想到01分数规划,二分答案mid,问题转化为判定是否存在一个生成树使 \(\sum (v_i-mid*w_i)\geq 0\),直接跑最大生成树即可。
最小瓶颈生成树
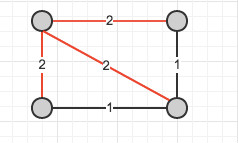
定义:最小瓶颈生成树是最大的边权值在所有生成树中最小的生成树。
定理:最小生成树一定是最小瓶颈生成树,但最小瓶颈生成树不一定是最小生成树.
前一个结论的证明:
假设最小生成树不是瓶颈树,设最小生成树T的最大权边为e,则存在一棵瓶颈树Tb,其所有的边的权值小于\(w_e\)。删除T中的e,形成两棵树T', T'',用Tb中连接T', T''的边连接这两棵树,得到新的生成树.因为任意的权值小于\(w_e\),新生成树的权值小于T,与T是最小生成树矛盾。
后一个结论的证明:
红边是一个最小瓶颈树。
Kruskal重构树
考虑Kruskal的过程,我们加入一条边\((x,y,w)\)的时候要合并\(x\)和\(y\)所在的连通块。我们可以新建一个节点\(z\),把\(x\)和\(y\)所在连通块在并查集上父亲设为\(z\),\(z\)的点权设为\(w\). 这样连边就形成了一棵树,称为Kruskal重构树
void kruskal(){//建出kruskal重构树
for(int i=1;i<=n*2;i++) fa[i]=i;
sort(E+1,E+1+m);
for(int i=1;i<=m;i++){
int x=E[i].from;
int y=E[i].to;
int fx=find(x);
int fy=find(y);
if(fx!=fy){
newn++;
//合并两个连通块,并向父亲连边
T.add_edge(fx,newn);
T.add_edge(fy,newn);
fa[fx]=newn;
fa[fy]=newn;
hi[newn]=E[i].len;//点权为边权
}
}
}
Kruskal重构树有如下性质:
-
Kruskal重构树是一个大根堆(默认是最小生成树,初始孤立点的权值为0)
-
任意两个点路径上边权的最大值为它们在Kruskal重构树的LCA的点权
[NOI2018] 归程
魔力之都可以抽象成一个 n 个节点、m 条边的无向连通图(节点的编号从 1 至 n)。我们依次用 l,a 描述一条边的长度、海拔。作为季风气候的代表城市,魔力之都时常有雨水相伴,因此道路积水总是不可避免的。由于整个城市的排水系统连通,因此有积水的边一定是海拔相对最低的一些边。我们用水位线来描述降雨的程度,它的意义是:所有海拔不超过水位线的边都是有积水的。
Yazid 是一名来自魔力之都的 OIer,刚参加完 ION2018 的他将踏上归程,回到他温暖的家。Yazid 的家恰好在魔力之都的 1 号节点。对于接下来 Q 天,每一天 Yazid 都会告诉你他的出发点 v ,以及当天的水位线 p。每一天,Yazid 在出发点都拥有一辆车。这辆车由于一些故障不能经过有积水的边。Yazid 可以在任意节点下车,这样接下来他就可以步行经过有积水的边。但车会被留在他下车的节点并不会再被使用。需要特殊说明的是,第二天车会被重置,这意味着:车会在新的出发点被准备好,且Yazid 不能利用之前在某处停放的车。
Yazid 非常讨厌在雨天步行,因此他希望在完成回家这一目标的同时,最小化他步行经过的边的总长度。
看到不能经过有积水的边,即不能经过边权小于一定值的边,我们想到了kruskal重构树。我们把边按海拔高度从大到小排序,然后建立一棵Kruskal重构树(最大生成树)。
我们在Kruskal重构树上从v开始树上倍增,找到最后一个高度>=水位线的点x,这样x子树中的点到起点的最小距离>=大于水位线,可以到达,而最小步行距离就是子树中叶子节点(它们对应原图中的节点)到1的最短路径长度最小值。
生成树计数
矩阵树定理(Matrix-Tree Theorem):
对于一个无向图\(G(V,E)\),定义它的拉普拉斯矩阵(Laplacian Matrix)
其中\(\operatorname{deg}\)表示点的度数。注意第二种情况如果有重边就\(=-\text{重边数}\).如果有自环就先删除。实际上拉普拉斯矩阵就是度数矩阵减去邻接矩阵。
无向图\(G\)的生成树个数相当于矩阵\(L\)去掉任意一行和一列后得到的矩阵\(L'\)(称为代数余子式)的行列式值
如何求矩阵的行列式值?
根据线性代数知识,行列式有以下性质:
- 如果把矩阵的某一行(列)加上另一行(列)的k倍,则行列式的值不变。
- 互换矩阵的两行(列),行列式变号。
- 上三角矩阵的行列式为主对角线乘积
采用高斯消元的方法,把矩阵消为一个上三角矩阵后,求出对角线的积.顺便记录消元过程中交换两行的次数来确定正负性。注意最后答案一定是整数,但中间直接除可能会产生精度误差,要采用辗转相除的方法,复杂度多一个log
ll gauss(int n){
//a是拉普拉斯矩阵
ll ans=1,sign=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) a[i][j]=(a[i][j]+mod)%mod;//消除负数
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
while(a[j][i]){//为了防止除不尽,要类似辗转相除法,整数消元
ll d=a[i][i]/a[j][i];
for(int k=1;k<=n;k++){
a[i][k]=(a[i][k]-d*a[j][k]%mod+mod)%mod;
swap(a[i][k],a[j][k]);
}
sign*=-1;//交换两行,行列式的值取负
}
}
if(!a[i][i]) return 0;//无解
ans=ans*a[i][i]%mod;//对于下三角矩阵,行列式的值为对角线乘积
}
ans=(ans*sign+mod)%mod;
return ans;
}
如果模数为质数,也可以直接用逆元求解。
[HEOI2015]小Z的房间
小 Z 突然有了一个大房子,房子里面有一些房间。事实上,小 Z 的房子可以看做是一个包含\(n \times m\)个格子的格状矩形,每个格子是一个房间或者是一个柱子。在一开始的时候,相邻的格子之间都有墙隔着。小 Z 想要打通一些相邻房间的墙,使得所有房间能够互相到达。在此过程中,小 Z 不能把房子给打穿,或者打通柱子(以及柱子旁边的墙)。同时,小 Z 不希望在房子中有小偷的时候会很难抓,所以你希望任意两个房间之间都只有一条通路。现在,小 Z 希望统计一共有多少种可行的方案。你能帮帮他吗?
板子题,每个房间和相邻房间之间建立无向边,对该图进行生成树计数。
代码
有向图的生成树似乎应该称作树形图?
设G=(V,E)是一个有向图,如果具有以下性质:
- G中不包含有向环;
- 存在一个顶点Vi,他不是任何弧的终点,而V的其他顶点都恰好是唯一的一条弧的终点。则称G是以Vi为根的树形图。
设有向图\(G(V,E)\)和一个根节点\(r\),我们重新定义拉普拉斯矩阵
\[L_{i,j}=\begin{cases} \operatorname{ind}_i,i=j \\ -1,i \neq j,(i,j) \in E \\ 0,\text{otherwise} \end{cases}\]其中\(\operatorname{ind}\)表示点的入度。重边处理同上。
有向图\(G\)的生成树个数相当于矩阵\(L\)去掉第\(r\)行第\(r\)列后得到的矩阵\(L'\)(称为代数余子式)的行列式值
这给我们一种求有向图生成树的方法。
[CQOI2018]社交网络
在一个实验性的小规模社交网络中我们发现,有时一条热门消息最终会被所有人转发。为了研究这一现象发生的过程,我们希望计算一条消息所有可能的转发途径有多少种。为了编程方便,我们将初始消息发送者编号为1,其他用户编号依次递增。该社交网络上的所有好友关系是已知的,也就是说对于A、B 两个用户,我们知道A 用户可以看到B 用户发送的消息。注意可能存在单向的好友关系,即lA 能看到B 的消息,但B 不能看到A 的消息。还有一个假设是,如果某用户看到他的多个好友转发了同一条消息,他只会选择从其中一个转发,最多转发一次消息。从不同好友的转发,被视为不同的情况。求一条被所有人转发消息的所有可能的转发途径。
板子题,求以1为根的生成树个数。
代码
矩阵树定理还有很多扩展运用,下面是简单的一个例子:
SDOI2014重建
连通分量
图的连通分量相关问题可以用Tarjan求解
无向图的割点与桥
割点与桥
定义:若去掉一个点后图的连通块个数增加,则这个点是割点. 若去掉一条边后图的连通块个数增加,则这条边是桥。
无向图上的Tarjan可以在\(O(n)\)时间内求解这个问题,只需要对图进行DFS。选定任意一个节点进行深度优先遍历,每个点仅访问一次。所有发生了递归的边会构成一棵树,我们称其为搜索树.(如果图不连通,要对每个连通块进行一次DFS,形成一个森林)
- \(dfn_x\): \(x\)的时间戳,根据第一次访问\(x\)的顺序给它编号,类似树的DFS序
- \(low_x\): \(x\)搜索树子树中的点和通过一条不在搜索树上的边能够到达\(x\)子树中的点的\(dfn\)的最小值
那么Tarjan过程如下
- 第一次访问节点\(x\)时,\(low_x\)设为\(dfn_x\).
- 遍历与\(x\)相邻的节点\(y\),若\(y\)是\(x\)的儿子,我们取\(low_x=\min(low_x,low_y)\),继承子树中的答案。否则属于第二类节点,取\(low_x=\min(low_x,dfn_y)\)
void tarjan(int x){
dfn[x]=++tim;
low[x]=dfn[x];
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}else low[x]=min(low[x],dfn[y]);
}
}
定理:无向边\((x,y)\)是桥,当且仅当\(y\)是\(x\)在搜索树上的一个子节点且满足\(dfn_x<low_y\).
证明: \(y\)的子树中的点沿着非搜索树的边向上走,不可能到达\(x\)的上方\(<dfn_x\)的位置,那就不会形成环。说明去掉\((x,y)\)后就不连通。
那么我们就可以写出求桥的代码。注意重边问题.
int tim=0;
int bridge_cnt=0;
void tarjan(int x,int last_edge){//last_edge记录从哪一条边递归来的
dfn[x]=++tim;
low[x]=dfn[x];
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(!dfn[y]){
tarjan(y,i);
low[x]=min(low[x],low[y]);
if(dfn[x]<low[y]){
is_bridge[i]=is_bridge[i^1]=1;
}
}
else if(i!=(last_edge^1)) low[x]=min(low[x],dfn[y]);
//如果有1条重边,重边不算非搜索树上的边,因此不能用它来更新.
}
}
定理: 若\(x\)不是搜索树的根节点,则 \(x\) 是割点当且仅当搜索树上存在一个\(x\)的子节点\(y\)且满足\(dfn_x \leq low_y\). 若\(x\) 是搜索树的根节点,则 \(x\) 是割点当且仅当搜索树上存在至少两个子节点\(y_1,y_2\) 满足上述条件。
证明:非根节点的情况和桥的证明类似。但是根节点如果只有一个儿子,去掉根节点后剩下的部分还是连通的,所以必须要两个子节点。
int tim=0;
int root=0;
int cutcnt=0;
void tarjan(int x){
dfn[x]=++tim;
low[x]=dfn[x];
int vcnt=0;
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
if(dfn[x]<=low[y]){
vcnt++;
if(vcnt>1||x!=root){
if(is_cut[x]==0) cutcnt++;
is_cut[x]=1;
}
}
}else low[x]=min(low[x],dfn[y]);
}
}
定义:
若一个无向图不存在割点,则称它为点双连通图。若一个无向图不存在桥,则称它为边双连通图。无向图的极大点双连通子图被称为点双连通分量(vertex double connected component,v-DCC),无向图的极大边双连通子图被称为边双连通分量(edge double connected component,v-DCC)
这里的“极大”指的是不存在包含这个双连通子图的更大的双连通子图。
定理:
一张无向图是边双连通子图,当且仅当任意一条边都包含在一个简单环(不自交的环)中。
一张无向图是点双连通子图,当且仅当图的顶点数不超过2,或图中任意两点都同时包含在至少一个简单环中。
e-DCC的求法与缩点
求出无向图中的所有的桥并打标记。再对无向图DFS,不访问桥边,每个连通块就是一个e-DCC.
把每个e-DCC看作一个节点,把桥边看作连接两点之间的边,会产生一棵树或森林。这种方法被称作缩点。缩点之后,可以用树上的算法维护图的一些信息,可参考树论.比如结合LCA之后可以处理无向图两点之间必经点或必经点边的询问。
int c[maxn];
int dcc=0;
void e_dcc(int x){
c[x]=dcc;
for(int i=head1[x];i;i=G[i].next){
int y=G[i].to;
if(c[y]||is_bridge[i]) continue;
e_dcc(y);
}
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
for(int i=1;i<=n;i++){
if(!c[i]){
dcc++;
e_dcc(i);
}
}
for(int i=2;i<=size1;i++){
int x=G[i].from;
int y=G[i].to;
if(c[x]==c[y]) continue;
else add_edge2(c[x],c[y]);
}
[Codeforces 555E]Case of Computer Network
给出一个无向图,以及q条有向路径。问是否存在一种给边定向的方案,使得这q条路径都能被满足。(如果有一条边是从a->b),而经过它的路径是从b->a,那么久不满足)。只需要判断,不用输出方案。
对于一个有向环,显然它可以允许各个方向的路径通过。所以我们只要把无向图里的边-双联通分量建成环,然后就不用考虑了。影响答案的只有桥。
所以我们求出所有桥,然后缩点,把图变成一棵树。
变成树之后考虑树上差分,给路径打标记。维护两个差分数组,一个表示向上的标记,一个表示向下的标记。对于一条路径u->v,只要up[u]++,up[lca(u,v)]--,down[v]++,down[lca(u,v)]--即可
注意原图可能不连通,所以如果路径的两端点不连通,直接输出No
代码&题解
v-DCC的求法与缩点,圆方树
与e-DCC不同,v-DCC不是删除割点后图中的连通块.实际上,每个割点可以属于多个v-DCC
求v-DCC的方法如下,在Tarjan的过程中维护一个栈:
- 当第一次访问某个节点的时候,把该节点入栈
- 如果\(dfn_x \leq low_y\),无论\(x\)是否为根,都要从栈顶不停弹出节点,直到节点\(y\)被弹出。刚才弹出的节点和\(x\)构成一个v-DCC. 可以用
vector存储一个v-DCC内的节点。
stack<int>s;
vector<int>v_dcc[maxn];
int root;
void tarjan(int x){
int flag=0;
dfn[x]=low[x]=++tim;
s.push(x);
for(int i=G.head[x];i;i=G.E[i].next){
int y=G.E[i].to;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
if(dfn[x]<=low[y]){
flag++;
if(x!=root||flag>1) cut[x]=1;
cnt++;
int z;
do{
z=s.top();
s.pop();
v_dcc[cnt].push_back(z);
}while(z!=y);
v_dcc[cnt].push_back(x);
}
}else low[x]=min(low[x],dfn[y]);
}
}
v-DCC的缩点比较复杂。假设图中有\(p\)个割点和\(q\)个v-DCC,我们建立一个有\(p+q\)个节点的新图,每个割点和包含它的所有v-DCC之间连边。这样建出的图是一棵树或森林。
void graph_to_tree(){
tim=cnt=0;//tim为时间戳,cnt为割点个数
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
newn=cnt;
for(int i=1;i<=n;i++){
if(cut[i]) belong[i]=++newn;//割点在新图编号为原图中的编号+割点个数cnt
}
for(int i=1;i<=cnt;i++){
for(int j=0;j<v_dcc[i].size();j++){
int x=v_dcc[i][j];
if(cut[x]){//对于每个割点,和包含它的v-DCC连边
T.add_edge(i,belong[x]);
T.add_edge(belong[x],i);
}
else belong[x]=i;
}
}
}
这棵树也被称为圆方树,每个割点被称为圆点,每一个v-DCC被称为方点。
[HNOI2012]矿场搭建
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。请写一个程序,用来计算至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
缩点,每个连通块形成一棵树。对于树上的点,分类讨论每个点双:
- 叶子节点(只含有一个割点的点双)必须建,任选1个非割点建
- 非叶节点(含有两个或两个以上的割点的点双)不用建,因为有两条路径通向另外两个点双
- 若缩点后只剩一个点,整个连通块都是点双连通的,那就必须要任选两个点建,这样任意一个坏掉都没关系。
有向图强连通分量
定义:若有向图中任意两点\(x,y\),既存在\(x\)到\(y\)的路径,也存在\(y\)到\(x\)的路径,则称该图为强连通图。有向图的极大强连通子图被称为强连通分量(Strongly Connected Component,SCC).
类似无向图的Tarjan算法,我们DFS这个图,会形成一棵搜索树(或森林).然后同样给每个点一个时间戳。图中的每条边\((x,y)\)一定是以下四种之一:
- 树边:\(x\)是\(y\)在搜索树上的父亲
- 前向边:\(x\)是\(y\)在搜索树上的祖先
- 后向边:\(y\)是\(x\)在搜索树上的祖先
- 横叉边: 除以上三种情况的边,它一定满足\(dfn_y<dfn_x\).(\(y\)已经被搜索过,所以搜索\(x\)的时候不用递归\(y\))
一个简单环一定是一个强连通图。因此我们需要找到后向边和横叉边,它们可能能到达\(x\)在搜索树上的祖先。
为了找到后向边和横叉边,我们需要维护一个栈,栈中存储一下两类节点:
- 搜索树上\(x\)的祖先节点。如果有后向边可以到达该节点,就可以形成环
- 已经访问过,并且存在一条路径到达\(x\)的祖先节点的节点。这样如果存在横叉边,就可以用这个点作为中转,到达\(x\)的祖先节点。
类似无向图的Tarjan,我们可以定义\(low_x\)为:在栈中且是\(x\)的子树出发的有向边的终点的所有节点最小时间戳。
定理: 若\(low_x=dfn_x\),则栈中从\(x\)到栈顶的所有节点构成一个强连通分量。
证明:我们不详细证明。\(low_x=dfn_x\)说明\(x\)子数中的节点不能和栈中的其他节点一起构成一个环. 另外,\(x\)子树中的节点也不可能直接到达尚未访问过的节点,否则就会继续递归下去。综上,这些节点不能和剩下的节点构成环。
那么我们就可以写出Tarjan的主过程:
- 当第一次访问\(x\)的时候,入栈\(x\),初始化\(dfn_x\)
- 对于与\(x\)相邻的所有节点\(y\): 若\(y\)没被访问过,递归\(y\),然后继承答案\(low_x=\min(low_x,low_y)\). 若\(y\)被访问过且\(y\)在栈中,更新\(low_x=\min(low_x,dfn_y)\).
- 若\(low_x=dfn_x\)成立,则不断从栈中弹出节点,直到\(x\)出栈。被弹出的节点构成一个SCC.
void tarjan(int x) {
ins[x]=1;//标记某个点是否入栈
s.push(x);
low[x]=dfn[x]=++num;
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(!dfn[y]) {
tarjan(y);
low[x]=min(low[x],low[y]);
} else if(ins[y]) {
low[x]=min(low[x],dfn[y]);
}
}
if(low[x]==dfn[x]) {
scc_cnt++;
int y;
do {
y=s.top();
ins[y]=0;
s.pop();
id[y]=scc_cnt;//记录每个点所在SCC编号
cntv[scc_cnt]++;
//记录SCC的信息
} while(y!=x);
}
}
有向图的缩点
类似无向图的缩点,把每个SCC看成一个点,相邻点连边,那么就会形成一个有向无环图(Directed Acyclic Graph,DAG).
[HAOI2006]受欢迎的牛
每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 A 喜欢 B,B 喜欢 C,那么 A 也喜欢 C。牛栏里共有 N 头奶牛,给定一些奶牛之间的爱慕关系,请你算出有多少头奶牛可以当明星。
受欢迎的奶牛只有可能是缩点后图中唯一的出度为零的SCC中的所有奶牛,所以若出现两个以上出度为0的强连通分量则不存在明星奶牛,因为那几个出度为零的SCC之间无法传递。
[SNOI2017]炸弹
在一条直线上有 n个炸弹,每个炸弹的坐标是\(x_i\) ,爆炸半径是\(r_i\) ,当一个炸弹爆炸时,如果另一个炸弹所在位置 满足:\(|x_j-x_i|\leq r_i\)那么,该炸弹也会被引爆。现在,请你帮忙计算一下,把第\(i\) 个炸弹引爆,将引爆多少个炸弹呢?
若x能引爆y,从x向y连一条有向边,最后的答案就是从x出发能够到达的点的个数
首先我们发现一个炸弹可以波及到的范围一定是坐标轴上的一段连续区间
我们可以用二分查找求出炸弹能波及到最左边和最右边的点,记为[l,r]
然后我们就需要向编号属于区间[l,r]的点连一条有向边
如果直接连边,时间复杂度为\(O(n^2)\) 无法接受,考虑用线段树优化连边
我们将线段树看成一个有向图,每个线段树节点看成图上的一个点,[l,r]向[l,mid],[mid+1,r]连边,叶子节点[l,l]向原图上的节点l连边
对于从x向编号属于区间[L,R]的点连边,我们用类似线段树区间更新的方法,将[L,R]拆成许多个小区间,再直接向这些小区间暴力连边
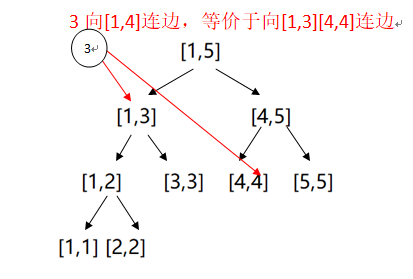
根据线段树的性质,最多会分出\(\left[ \log _{2}n\right]\)个节点,所以单次连边的时间复杂度为\(O(\log n)\)
然后就很套路了,显然环上的点可以缩成一个大点(权值为环上所有节点权值之和(线段树节点权值为0,原图上节点权值为1))
Tarjan完在DAG上DP即可代码&题解
2-SAT
有\(n\)个变量,每个变量只有2种取值,再给定\(m\)个条件,每个条件都是对两个变量的取值限制,形如:若变量\(A_i\)赋值为\(A_{i,p}\),则变量\(A_j\)赋值为\(A_{j,q}(p,q \in \{ 0,1\})\).
求是否存在一种满足所有条件的赋值方案。这个问题被称为2-SAT问题,解法如下:
- 建立\(2n\)个节点的无向图,每个变量的2种取值对应2个节点\(i,i+n\)
- 对于每个条件,连从\(i+np\)到\(j+nq\)的有向边\((i+np,j+nq)\). 注意每个命题都对应一个逆否命题,若在\(m\)个条件中原命题和逆否命题不成对出现,那么要连边\((j+(1-q)n,i+(1-p)n)\)
- 用Tarjan算法求强连通分量
- 若\(\exist i \in [1,n]\),满足\(i\)和\(i+n\)属于同一个强连通分量,则表明若第\(i\)个变量被赋值为\(A_{i,p}\),那么第\(i\)个变量被赋值为\(A_{i,1-p}\),矛盾。所以这种情况无解。
时间复杂度\(O(n+m)\)
刚刚我们只解决了判定。如何构造一种合法方案?显然一个变量的赋值状态确定了,那么该点所在SCC内的变量的状态也确定了. 那我们可以缩点,然后对原图拓扑序。发现一个无出边的点无论怎么赋值都没有影响。因此可以按拓扑序逆序对点赋值。若\(i\)的拓扑序比\(i+n\)大,就把第\(i\)个变量赋值为\(A_{i,0}\),反之亦然。 另外实际上因为Tarjan是回溯的时候标记SCC的,所以求出的SCC编号越小的实际上拓扑序越大,因此条件可以改为若\(i\)的SCC编号比\(i+n\)小,就把第\(i\)个变量赋值为\(A_{i,0}\),反之亦然
bool check(){
for(int i=1;i<=n*2;i++){
if(!dfn[i]) tarjan(i);
}
for(int i=1;i<=n;i++){
if(bel[i]==bel[i+n]) return 0;
}
return 1;
}
int main(){
int u,v,p,q;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d %d %d %d",&u,&p,&v,&q);
add_edge(u+(1-p)*n,v+q*n);//如果u不为p,那么v一定为q,否则就不满足条件了
add_edge(v+(1-q)*n,u+p*n);
}
if(check()){
puts("POSSIBLE");
for(int i=1;i<=n;i++){
if(bel[i]<bel[i+n]) printf("0 ");
else printf("1 ");
}
}else puts("IMPOSSIBLE");
}
注意如果要求字典序最小解(如BZOJ2199),似乎只能暴力枚举。复杂度\(O(nm)\)
int mark[maxn*2+5];
void dfs(int x){
mark[x]=1;
for(int y : E[x]){
if(!mark[y]) dfs(y);
}
}
bool check(int x){
for(int i=1;i<=n*2;i++) mark[i]=0;
dfs(x);
for(int i=1;i<=n;i++){
if(mark[i]&&mark[i+n]) return 0;
}
return 1;
}
int main(){
for(int i=1;i<=n;i++){
flag1=check(i);
flag2=check(i+n);
if(!flag1&&!flag2){
printf("IMPOSSIBLE\n");//无解
return 0;
}else if(flag1&&!flag2){
ans[i]='Y';//选0
}else if(!flag1&&flag2){
ans[i]='N';//选1
}else{
ans[i]='?';//怎么选都可以
}
}
}
[POI2001]和平委员会
每个党派都在委员会中恰有 1 个代表。如果 2个代表彼此厌恶,则他们不能都属于委员会。每个党在议会中有 2 个代表。代表从 1 编号到 2n。 编号为 2i-1和 2i 的代表属于第 i 个党派。任务:写一程序读入党派的数量和关系不友好的代表对,计算决定建立和平委员会是否可能,若行,则列出委员会的成员表。
板子题.代码
[NOI2017]游戏
小 L 计划进行 n 场游戏,每场游戏使用一张地图,小 L 会选择一辆车在该地图上完成游戏。小 L 的赛车有三辆,分别用大写字母 A、B、C 表示。地图一共有四种,分别用小写字母 x、a、b、c 表示。其中,赛车 A 不适合在地图 a 上使用,赛车 B 不适合在地图 b 上使用,赛车 C 不适合在地图 c 上使用,而地图 x 则适合所有赛车参加。适合所有赛车参加的地图并不多见,最多只会有 d 张。小 L 对游戏有一些特殊的要求,这些要求可以用四元组 (i,hi,j,hj) 来描述,表示若在第 i 场使用型号为 hi 的车子,则第 j 场游戏要使用型号为 hj 的车子。你能帮小 L 选择每场游戏使用的赛车吗?如果有多种方案,输出任意一种方案。如果无解,输出 −1 。
\(1≤n≤50000,0≤d≤8\)
看到这些约束,应该想到这是类似2-SAT的问题。但是x地图很麻烦,因为k-SAT问题在k>2的时候是NPC问题,所以不能直接做。
观察到\(d \leq 8\),我们可以直接枚举每个x地图可以让哪些车使用,然后把它转换成标准的2-SAT问题。把每场拆成两个点,分别表示第i场游戏使用该地图适合的第一种赛车和第二种赛车.枚举的时间复杂度\(2^d\)。对于枚举的每一种情况,我们现在已经得到了每个地图适合哪些车参加,然后考虑建图。
定义若每个地图可以参加的车种类为x和y,第一种车为x,y中字典序较小的,第二种车为字典序较大的。把每个地图拆成两个点,第一个点表示第一种车,第二个点表示第二种车
然后是限制
- 如果限制i的第一个地图\(a_i\)不适合型号为\(x_i\)的车,那么不做任何操作
- 如果限制i的第二个地图\(b_i\)不适合型号为\(y_i\)的车,那么\(a_i\)场不能选\(h_i\),只能选\(x_i\)外符合条件的另一辆车,\(b_i\)场只能选除\(y_i\)外符合条件的另一辆车。两辆车对应的点之间连边即可
- 如果1,2的情况都满足,只需要判断一下可以选的车即可,细节比较复杂,见代码
建完图之后跑2-SAT即可,输出答案的时候注意判断一下这个点对应的车种类到底是A,B还是C
时间复杂度\(O(2^d(n+m))\),代码&题解
二分图
定义:如果一个无向图的\(n\)个点可以分成两个集合\(A,B\),其中\(A \cap B=\empty\),并且同一集合内的点没有边相连,那么称这个图为二分图。其中\(A,B\)分别称为二分图的左部和右部
二分图判定
定理:一张无向图是二分图,当且仅当图中不存在奇环。
根据该定理,我们可以用染色法进行二分图判定。时间复杂度\(O(n+m)\)
void dfs(int x,int color){
v[x]=color;
for(int i=0;i<E[x].size();i++){
int y=E[x][i];
if(!v[y]){
dfs(y,3-color);
}else if(v[y]==color){//如果一条边的两端颜色相同,就不是二分图
flag=false;
}
}
}
二分图匹配
定义:任意两条边都没有公共端点的边集称为图的一组匹配。在二分图中,包含边数最多的匹配被称为二分图的最大匹配。
对于任意一组匹配,属于它的边被称为匹配边,其他的边被称为非匹配边。匹配边的端点被称为匹配点,其他的点被称为非匹配点。如果在二分图中出现连接两个非匹配点的路径,且匹配边和非匹配边在路径上交错出现,那么称这条路为增广路
增广路显然具有以下性质:
- 长度\(len\)为奇数
- 第\(1,3,5 \dots len\)边为非匹配边,第\(2,4,6 \dots len-1\)为匹配边
- 将增广路上的边取反(匹配边和非匹配边交换),匹配边个数+1
- 二分图的一组匹配是最大匹配,当且仅当图中不存在增广路
根据这些性质,我们可以得到匈牙利算法。
- 把所有边设为非匹配边
- 递归找到一条增广路。对于每个左部节点\(x\),遍历相邻的所有右部节点\(y\),若\(x\)和\(y\)匹配,要么\(y\)是非匹配点,要么\(y\)的匹配\(z\)可以找到另一个右部点和它匹配。回溯时取反增广路状态
- 重复第2步,直到不存在增广路。
这是一个贪心算法,正确性显然。由于每个点要遍历整个图一次,时间复杂度\(O(nm)\).另外用最大流算法可以做到\(O(n \sqrt m)\),但常数和代码量较大,见网络流
int vis[maxn];//防止重复访问的标记
int match[maxn];
bool dfs(int x){
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(!vis[y]){
vis[y]=1;
if(!match[y]/*尚未匹配*/||dfs(match[y])/*原来的匹配点可以找到新的匹配*/){
match[y]=x;
return 1;
}
}
}
return 0;
}
int main(){
for(int i=1;i<=e;i++){
scanf("%d %d",&u,&v);
add_edge(u,v);//匈牙利算法只需要加单向边!
}
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if(dfs(i)) ans++;
}
}
二分图匹配的模型有两大要素:
- 节点能分成两个集合,每个集合内部没有边
- 每个节点只能和一条匹配边相连。
其中常见的模型是棋盘问题
[ZJOI2007]矩阵游戏
小Q是一个非常聪明的孩子,除了国际象棋,他还很喜欢玩一个电脑益智游戏——矩阵游戏。矩阵游戏在一个N*N黑白方阵进行(如同国际象棋一般,只是颜色是随意的)。每次可以对该矩阵进行两种操作:行交换操作:选择矩阵的任意两行,交换这两行(即交换对应格子的颜色)列交换操作:选择矩阵的任意行列,交换这两列(即交换对应格子的颜色)游戏的目标,即通过若干次操作,使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。对于某些关卡,小Q百思不得其解,以致他开始怀疑这些关卡是不是根本就是无解的!!于是小Q决定写一个程序来判断这些关卡是否有解。
游戏的操作有以下性质:
- 如果两个格子在同一列,那么无论如何操作,这两个格子都在同一列。
- 如果两个格子在同一行,那么无论如何操作,这两个格子都在同一行。
- 可以通过操作改变改点在对应行和列中的位置。
我们发现对于第i行,我们必须要找到某一列上的黑格子挪过来放在对角线上,相当于每一行必须和每一列一一对应.所以对于黑格子(i,j),我们将i向j连边,跑二分图匹配如果答案为n则有解,否则无解.
二分图最小点覆盖,最大团,最大独立集
定义:给定一张二分图,求出最小的点集S使得图中任意一条边都至少有一个端点被覆盖,这个问题被称为二分图的最小点覆盖
定理:二分图最小点覆盖=二分图最大匹配
定义:二分图的独立集是任意两点之间都没有边相连的点集,包含点数最多的一个就是最大独立集。反过来,团是任意两点之间都有边相连的点集,包含点数最多的一个就是最大团
定理:二分图最大独立集=点数-最大匹配
定理:任意无向图的最大团=补图最大独立集
对于一般图,最大团和最大独立集是NPC问题。
这些问题在网络流中会详细讨论。另外二分图匹配的扩展,如多重匹配和带权匹配也在那一节中。
欧拉图
定义: 欧拉路径是一条能够不重不漏地经过图上的每一条边的路径.欧拉回路是一条能够不重不漏地经过图上的每一条边的路径,且起点和终点相同。
定理:
无向图欧拉回路的判定:图G为连通图,所有顶点的度为偶数。
无向图欧拉路径的判定:图G为连通图,除有2个顶点度为奇数外(这2个点为路径端点),其他顶点度都为偶数。
有向图欧拉回路的判定:图G的基图联通,所有顶点的入度等于出度。
有向图欧拉路径的判定:图G的基图联通,有且只有2个点的入度分别比出度大1和少1(这2个点为路径端点),其余所有顶点的入度等于出度。
求欧拉路径可以直接用DFS实现。遍历每个节点的边\((x,y)\),若该边没被访问过,就标记并把\(y\)入栈,继续递归。用类似Dinic算法的当前弧优化,每次访问后令邻接表的\(head_x\)指向下一条边,这样就不会重复访问。复杂度\(O(n+m)\)
int stk[maxn+5],top;
int vis2[maxm+5];//标记边
void dfs(int x){
stk[++top]=x;
for(int &i=head[x];i;i=E[i].next){
int y=E[i].to;
if(!vis2[i]){
vis2[i]=vis2[i^1]=1;
dfs(y);
}
}
}
[Codeforces547D]
给定二维平面上的n个点的坐标.求一个方案把每个点用红色或蓝色染色,使得水平共线或者垂直共线的点中红色与蓝色数量差不超过1.
先对坐标离散化,每个x坐标和y坐标建一个点。我们把每个点看作连接两个坐标的边.那么就是求染色方案使每个点的边中红色和蓝色数量差不超过1
如果图存在欧拉回路,那么直接把回路上的边交错染色,这样每个点出入的次数相同,差等于0.如果有奇点,两个两个配对连一条虚边,然后求欧拉回路,将上面的边交错染色


 浙公网安备 33010602011771号
浙公网安备 33010602011771号