网络流常见建图套路总结(重制版)
网络流常见建图套路总结(重制版)
前置知识
- 网络流的基本算法:Dinic最大流,EK+SPFA求费用流
- 最小割,最小割最大流定理
- 二分图判定,匹配,相关性质
由于本文以建图方法为主,不涉及网络流算法的具体实现,以上前置知识一边看一边学也可以

最大流
二分图最大匹配与多重匹配
二分图匹配:给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不相交,则称M是一个匹配。二分图最大匹配则是使边数最多的匹配
二分图多重匹配:每个节点不一定只与一条边相连,而是限制了最多连的边数(当限制为1时退化为二分图最大匹配
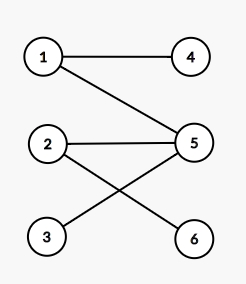
建图方法:
对于一张二分图,我们可以从源点S向左部节点连有向边,右部节点向汇点T连有向边,原二分图每条边看作从左到右的有向边
假如把所有边的流量设为1,则二分图的最大匹配数就等于S到T最大流,所有有流经过的边为匹配边
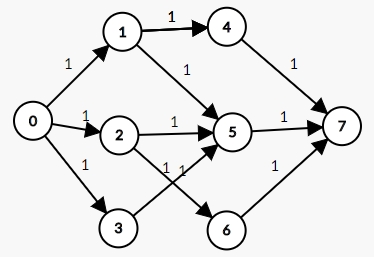
如果要求二分图多重匹配,则只需把S向左部点的有向边容量设为左部点匹配数量上限,右部点同理
二分图一般匹配:飞行员配对方案问题
二分图多重匹配:圆桌问题
二分图的建模有两个要素:
- 0要素:能分成两个不相交的点集
- 1要素:一个点只能与一条边相连
最小路径覆盖
最小路径覆盖:在一个有向无环图中,找出最少的路径,使得这些路径经过了所有的点。最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖,区别是这些路径是否可以相交
最小不相交路径覆盖
建图方法:把原图的每个点u拆成两个点\(u_1,u_2\),如果有一条有向边\((a,b)\),则连边\((a_2,b_1)\),容易发现这是一个二分图,那么用下面的定理就可以求出答案
定理: 最小路径覆盖=原图节点数-新图最大匹配数
证明:
一开始每个点都是一条路径,每次找一条匹配边,代表合并两条路径
由于路径不相交(即每个点的入度和出度至少有一个为1),所以二分图上的边也不相交(如果相交则说明某个点的入度或出度大于1),这正好是匹配的定义
每条匹配边代表答案-1,所以最小路径覆盖=原图节点数-新图最大匹配数
最小可相交路径覆盖
对原图传递闭包,即若原图中\((u,v)\)连通,则增加边\((u,v)\).这可以用Floyd算法\(O(n^3)\)实现。然后对新图做最小不相交路径覆盖即可。因为在原图中相交的路径在传递闭包后可以拆分成另一条边,这样就不相交了
最小路径覆盖:
最小路径覆盖问题
最多不相交路径
这种问题变化比较多,但都能表示成以下形式:
已知一些路径,每个节点只能属于一条路径,求能选择多少条路径使它们不相交.
主要的方法是拆点,将一个点拆成两个,然后连边,容量表示该点最多经过次数
最小割
最大权闭合子图
定义:有一个有向图,每一个点都有一个权值,选择一个权值和最大的子图,使得每个点的后继都在子图里面,这个子图就叫最大权闭合子图。
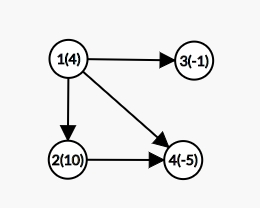
如图,括号外的为点的编号,括号内的为点的权值,则闭合子图有{1,2,3,4} {2,4} {3} {4}{空},最大的闭合子图是{1,2,3,4},权值和为8
建图方法:
从源点s向每个正权点连一条容量为权值的边,每个负权点向汇点t连一条容量为权值的绝对值的边,有向图原来的边容量全部为无限大。
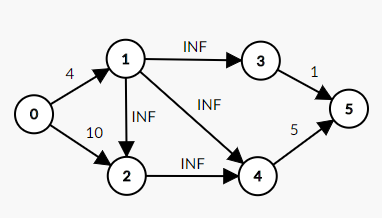
定理:最大权闭合子图=所有正权点之和-最小割
证明:
关键性质:如果s与i有边,表示i在子图中。如果i与t有边,表示i不在于子图中。即:割掉s与i表示不选i,割掉i与t表示选i。
性质1:原图之间的边一定不会被割掉
边权为无穷大,当然不会被选进最小割
性质2:只有s到t不联通时,才得到最大权闭合子图
反证法:若s到t连通,则一定存在节点i,j使s到i有边,i到j有边(引理1),j到t有边.而根据性质1:i在子图中,j不在子图中,这与最大权闭合子图的定义矛盾,证毕
由引理2可得,图的一个割就是一个闭合子图
由于\(一个割的边权和=不选的正权点+选的负权点绝对值=不选的正权点-选的负权点\).
显然割的边权和最小的时候得到最大权闭合子图,证毕
应用:
当问题中出现一种冲突时,就可以采用最大权闭合子图。具体来说,对于一个事件,只能得到a收益和b收益之中的一种。我们就把a收益作为正权点,b收益作为负权点,跑最大权闭合子图
二分图独立集
定理: 二分图最大独立集=n-二分图最大匹配
其实二分图独立集是特殊的一种最大权闭合子图。我们根据上文“收益”的思想,把选某个点的收益看为1,左部节点为正权点,右部节点为负权点.按照最大权闭合子图的方式建图,答案为正权和-最小割=n-最小割=n-最大流。我们发现把最大权闭合子图中INF的边换成1也不影响答案,因为图中其他边的容量都为1。这样图就变成了二分图匹配中的图,最大流=二分图最大匹配
例题:
最大密度子图
定义:图的密度是图上的边的数量除以点数。求密度最大的子图。
建图:看到平均数想到01分数规划。二分答案\(mid\),那么问题转化为判定是否存在一个子图,使得\(边数-mid\cdot 点数>0\).那么可以把每条边的权看成1,每个点的权看成\(-mid\),限制是选择一条边就必须选择边连接的两个点。于是把边看成左部点,点看成右部点,跑最大权闭合子图,若答案\(>0\),则合法。
二元关系最小割模型
定义:有若干个变量,每个变量有2种取值,有若干个现在,每个限制形如"若变量x=a,y=b,就要付出c的代价"。最大化所有变量的值之和减去最小代价。
建图:每个变量建一个点,S到x连边表示x的一种取值的代价,x到T连边表示x的另一种取值的代价。对于一个限制,在两个点之间连边。边权需要列方程解出。
平面图最小割
定义:平面图是指能够所有边画在一个平面上使得每条边仅在顶点处相交的图.现在给出一张边带权的平面图与起点和终点,求一个边权和最小的边集,使得去掉这个边集后起点和终点不连通。
建图:
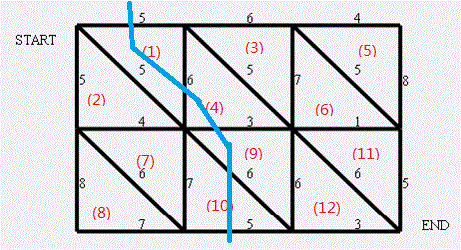
我们发现,如果把每个平面区域看成一个点,交界处的边看成连接两个区域的边,再加两个点表示分割线的起点和终点、那么原图的一个割就对应新图的一条路径。如图上S->(1)->(4)->(9)->(10)->T就构成了一个分割线,割断的边权为5,6,3,6,5.因此原图的最小割就等价于新图上的最短路,我们将新图称为这个平面图的对偶图。也就是说,平面图最小割=对偶图最短路
对于一般的平面图,找出这些区域需要一些计算几何的知识,这里不(wo)再(ye)赘(bu)述(hui).但是很多题目中出现的图往往是有规律的,比如网格图.那么就可以直接建图跑最短路求解,往往能获得比网络流优的多的复杂度。
最小割的方案
求最小割的边集。
最小割的可行边
定理:边\((u,v)\)是可行边,当且仅当\((u,v)\)满流,且残量网络上不存在\(u\)到\(v\)的路径
如果还有路径,说明可以继续增广,
注意到\((u,v)\)满流时\((v,u)\)在残量网络上,那么判定定理也可以写成:\((u,v)\)满流,且残量网络上\(u,v\)不在同一个强连通分量(SCC)里
我们将SCC缩点,那么新图的任意最小割都是原图的最小割,其中肯定有把\(u,v\)所在SCC割开的最小割。这就证明了上述定理.
代码实现上可以Tarjan缩点,但是直接BFS似乎跑的也很快
最小割的必须边
同上求SCC,设\(id_x\)为\(x\)的SCC编号。
定理:对于满流边\((u,v)\),若\(id_s=id_u\)且 \(id_v=id_t\),那么边\((u,v)\)是必须边。
证明:如果一条边是必须的,那么增加这条边的容量一定会改变最大流。
残量网络的SCC缩点后是一个DAG,方向是从T向S
当且仅当\((u,v)\)刚好在\(id_s\)和\(id_t\)之间时,增加\((u,v)\)的流量才能增大最大流。
最小割任意方案和字典序最小方案
依次枚举每条边(枚举顺序不同,方案也不同).每次选取一条满流边\((u,v)\),用BFS判断它是否是可行边。如果是就加入最小割。考虑经过\((u,v)\)的增广路,这条路上的满流边也可能成为割边,这样就会和\((u,v)\)重复。因此要退回这些边的流量,让它们不满流,就不会被选进去了。具体方法是从\(u\)向\(s\),\(v\)向\(t\)跑一次Dinic,相当于把流量流回去,这一步被称为退流。
如果让字典序最小,就按编号从小到大枚举即可。题目要求的特定顺序也类似.
最小割最小边数方案
跑完一次最小割后,令所有满流边容量为1,非满流边容量为\(+\infty\).再做一次最小割,此时的任意最小割方案割边都最少。
分层图最短路与最大流
分层图最短路
分层图是一种状态是多维的的图,它是由一个图不断复制形成的
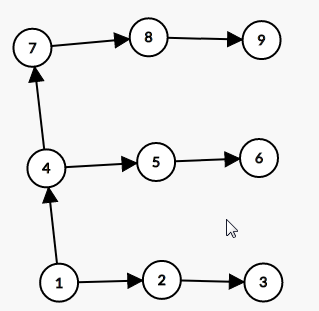
这就是一个分层图,它由图{1,2,3}复制了三次形成
通常情况下须要用到分层图的题目都有一些操作,操作可能会改变边权或者连边方式,我们的解决方法就是把原图复制,然后修改,并在不同层次图的点之间连起新的边。 每一层图都是由原图复制来的。因此这些不同层次的图的结构和性质类似
在实现上,邻接表里不一定要存储所有的边,可以只存储原图,但是一些数组用二维数组来表示,如\(dist[i][u]\)表示第i层的u号节点
这是分层图上的spfa算法的(伪)代码
struct node{
int floor;//层数
int num;//节点编号
}
queue<node>q;
int dist[maxl][maxn];//距离
int inq[maxl][maxn];//是否在队列种
int spfa(node s,node t){
q.push(s);
memset(dist,0x3f,sizeof(dist));
dist[s.floor][s.num]=0;
while(!q.empty()){
node x=q.front();
q.pop();
inq[x.floor][x.num]=0;
for(y : 从x可以到达的节点){
if(dist[y.floor][y.num]>dist[y.floor][y.num]+w){//w为转移代价
dist[y.floor][y.num]=dist[y.floor][y.num]+w;
if(!inq[y.floor][y.num]){
inq[y.floor][y.num]=1;
q.push(y);
}
}
}
}
return dist[t.floor][t.num];
}
很多时候分层图最短路也可以通过BFS解决,但SPFA会稍快一些
分层图最大流
建图:把分层图加上流量即可
例题:家园
费用流
费用流的建图一般没有固定套路,要根据具体问题在流上加上费用。在处理费用流的情况下,一定要注意一点:EK+SPFA求的是在流量最大的前提下的最小费用,有时会发现建图不需要满足流量最大,此时要考虑改变建图方式或使用有上下界的费用流。
另外,费用流的复杂度较高,Dinic能跑过的单路增广+SPFA未必能跑过,可以考虑多路增广+SPFA或zkw费用流。
二分图带权匹配
定义:每条边有边权,求匹配边权值之和最大的匹配
建图:在边上加上权,跑费用流即可
最大权不相交路径
定义::每条路径有一个权值(一般是边权和),在不相交路径数最多的情况下,最大化费用
建图:同最多不相交路径,在连接两个拆点的边上加上费用跑费用流即可
不等式差分模型(网络流解线性规划)
定义:对于一些不太好直接想到建图的问题,我们可以数学建模,列出方程然后用线性规划求解。这样的好处是思维量较小,只要做代数变换就可以建图,而不用考虑建图的实际意义。我们需要把式子做差,使得每个未知数仅在两个等式中出现。
根据网络流中每个点流量平衡的思想,我们可以把\(−x_i\)看成从点\(i\)流出xi的流量,\(+x_i\)看成流入\(x)i\)的流量。等式为0就代表流量平衡。
建图:
-
每个等式为图中一个顶点,添加源点S和汇点T。
-
如果一个等式右边为非负整数c,从源点S向该等式对应的顶点连接一条容量为c,权值为0的有向边;如果一个等式右边为负整数c,从该等式对应的顶点向汇点T连接一条容量为c,权值为0的有向边。
-
如果一个变量\(x_i\)在第j个等式中出现为\(x_i\),在第k个等式中出现为\(-x_i\),且在目标函数里的系数为\(c_i\),从顶点j向顶点k连接一条容量为\(+\infty\),费用为\(c_i\)的有向边。
-
如果一个变量\(y_i\)在第j个等式中出现为\(y_i\),在第k个等式中出现为\(-y_i\),且在目标函数里没有出现,从顶点j向顶点k连接一条容量为\(+\infty\),权值为0的有向边。
例题:志愿者招募
例题:餐巾计划问题
有上下界的网络流
无源汇有上下界可行流
定义: 无源汇网络指的是没有源点和汇点,每个点都有入边和出边且满足流量守恒的网络。在这个网络上求一个流量方案,使得每条边的流量必须在\([l_i,r_i]\)之间,且每个点流量守恒。
有上下界的费用流的核心是"补偿"。我们先假设每条边的流量均为\(l_i\),那么一定会有一些点流量不守恒。现在我们需要构造一个附加网络,使得把附加网络和原网络叠加(即对应边流量相加)之后的图满足流量守恒。
因为Dinic只能求有源汇最大流,所以是不能直接求出附加网络的流量的。那么我们可以在附加网络上添加一些不在原网络上的边和点,来实现我们的限制.
记\(d_i=\text{点}i\text{的入流}-\text{点}i\text{的出流}\),然后建附加网络:
- 新建源点\(ss\)和汇点\(tt\)
- 对于原图中的每条边\(e_i=(u,v)\),连边\((u,v,r_i-l_i)\),也就是说附加网络包括原网络的边。
- 新建边来满足流量守恒
- 若\(d_i=0\)则该点流量平衡,不用处理
- 若\(d_i>0\)则入流>出流,那么附加网络中\(i\)的出边需要增加流量,我们连边\((ss,i,d_i)\),这样求最大流的时候出边的流量会增加\(d_i\),叠加后满足流量守恒
- 若\(d_i<0\)则入流<出流,那么附加网络中\(i\)的入边需要增加流量,同理连边\((i,tt,-d_i)\),这样求最大流的时候入边的流量会增加\(-d_i\),叠加后满足流量守恒
那么当且仅当步骤3中新建边满流时有解,总可行流为\(\mathrm{maxflow} (ss,tt)+\sum l_i\)。每条边在原图中流量=容量下界+附加流中它的流量
有源汇有上下界可行流
定义: 在有源汇网络上求一个流量方案,使得每条边的流量必须在\([l_i,r_i]\)之间,且除源汇外每个点流量守恒。
设原网络的源和汇分别为\(s,t\)我们在原网络上加一条边\((t,s,+\infty)\),相当于把到汇点的所有流量都流回源点,这样每个点流量都守恒。
然后套无源汇的方法即可。注意总流量=t到s的无穷边在原图中的流量
有源汇有上下界最大流和最小流
定义: 在有源汇网络上求一个流量方案,使得每条边的流量必须在\([l_i,r_i]\)之间,且除源汇外每个点流量守恒。在这个条件下使得总流量最大/最小。
先按上面的方法求出一个有源汇有上下界可行流.然后在附加网络上再跑一次\(s\)到\(t\)的最大流(注意不是ss,tt!)。最大流=可行流+第二次跑的s到t最大流。
再跑一次最大流是因为附加网络上属于原图的边还有流量没被“榨干”。容易发现只要附加网络上不属于原图的边满流,属于原图的边怎么跑流量都是守恒的。因为第一次跑最大流已经保证所有点守恒,第二次跑最大流不会经过不属于原图的边,因此等价于对原图跑一次普通的最大流,除源汇外流量守恒。两次合起来总流量一定守恒,这就保证了正确性。
同理求最小流就跑一次\(t\)到\(s\)的最大流。最小流=可行流-第二次跑的t到s最大流。这是因为Dinic过程中反向边的流量增加等价于正向边的的流量减少。
有源汇有上下界最小费用流
定义: 在有源汇网络上求一个流量方案,使得每条边的流量必须在\([l_i,r_i]\)之间,且除源汇外每个点流量守恒。每条边单位流量的费用为\(c_i\).在这个条件下使得总费用最小,费用定义同一般费用流。(不要求总流量最大)
这是有上下界费用流常被误解的一点,即最小费用流求的是费用最小的可行流,而不是最大流。
因此按有源汇可行流的方法建图,把原图中的边带上费用。总费用=\(\text{mincost}(ss,tt)+\sum l_ic_i\)
ll solve(int s,int t){
ll ans=0;
int ss=cntv+1,tt=cntv+2;
adde(t,s,0,INF,0);
for(int i=1;i<=cnte;i++){
dflow[E[i].from]-=E[i].lflow;
dflow[E[i].to]+=E[i].lflow;
ans+=E[i].lflow*E[i].cost;
MCMF::add_edge(E[i].from,E[i].to,E[i].rflow-E[i].lflow,E[i].cost);
}
for(int i=0;i<=cntv;i++){
if(dflow[i]>0) MCMF::add_edge(ss,i,dflow[i],0);
else if(dflow[i]<0) MCMF::add_edge(i,tt,-dflow[i],0);
}
return ans+MCMF::mcmf(ss,tt);
}
例题:
一些连边技巧总结
多源汇点: 建立超级源和超级汇
节点容量::拆点,两个拆点之间的边容量为节点的容量。注意一些费用流问题里不能把两个点直接相连,因为费用流的前提最大流可能会导致建图与实际意义不符,即这条边被强行跑满。如果一定要这样做,可以加上下界。
费用与流量平方成正比:拆边,设系数为\(a\),把拆边的费用设为$a,3a,5a\dots $,容量设成1,又因为费用流会按费用从小到大增广,那么最终费用会是 \(a,4a,9a\dots\)
网络流的技巧还有很多,尤其是一些题目需要流,割等概念的意义的深刻理解,水平所限,这种比较玄学的部分只能留给读者了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号