[BZOJ1001]狼抓兔子(平面图最小割)

[BZOJ1001]狼抓兔子(平面图最小割)

题面

略

分析

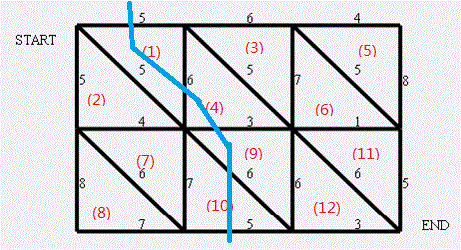
我们发现,如果把每个平面区域看成一个点,交界处的边看成连接两个区域的边,再加两个点表示分割线的起点和终点、那么原图的一个割就对应新图的一条路径。如图上S->(1)->(4)->(9)->(10)->T就构成了一个分割线,割断的边权为5,6,3,6,5.因此原图的最小割就等价于新图上的最短路,我们将新图称为这个平面图的对偶图。也就是说,平面图最小割=对偶图最短路

于是建出对偶图。代码中\(id[i][j][0/1]\)分别表示\((i,j)\)格被分成的上半区域和下半区域。用Dijkstra求最短路

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxs 1000
#define maxn 2200000
using namespace std;
int n,m;
struct edge {
	int from;
	int to;
	int len;
	int next;
} E[maxn*3+5];
int head[maxn+5];
int esz=1;
void add_edge(int u,int v,int w) {
//	printf("%d-%d len=%d\n",u,v,w);
	esz++;
	E[esz].from=u;
	E[esz].to=v;
	E[esz].len=w;
	E[esz].next=head[u];
	head[u]=esz;
	esz++;
	E[esz].from=v;
	E[esz].to=u;
	E[esz].len=w;
	E[esz].next=head[v];
	head[v]=esz;
}

struct node {
	int id;
	int dist;
	node() {

	}
	node(int _id,int _dist) {
		id=_id;
		dist=_dist;
	}
	friend bool operator < (node p,node q) {
		return p.dist>q.dist;
	}
};
bool vis[maxn+5];
int dist[maxn+5];
int dijkstra(int s,int t) {
	priority_queue<node>q;
	memset(vis,0,sizeof(vis));
	memset(dist,0x3f,sizeof(dist));
	dist[s]=0;
	q.push(node(s,0));
	while(!q.empty()) {
		int x=q.top().id;
		q.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=head[x]; i; i=E[i].next) {
			int y=E[i].to;
			if(dist[y]>dist[x]+E[i].len) {
				dist[y]=dist[x]+E[i].len;
				if(!vis[y]) q.push(node(y,dist[y]));
			}
		}
	}
	return dist[t];
}
int id[maxs+5][maxs+5][2];
int main() {
	int ptr=0,x;
	scanf("%d %d",&n,&m);
	int s=0,t;
	for(int i=1;i<n;i++){
		for(int j=1;j<m;j++){
			id[i][j][0]=++ptr;//(i,j)格的上半部分 
			id[i][j][1]=++ptr;//下半 
		}
	}
	t=ptr+1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<m;j++){
			scanf("%d",&x);
			if(i==1) add_edge(s,id[i][j][0],x);
			else if(i==n) add_edge(id[n-1][j][1],t,x);
			else add_edge(id[i-1][j][1],id[i][j][0],x);//横线分开了(i,j-1)的下半和(i,j)的上半 
		}
	}
	for(int i=1;i<n;i++){
		for(int j=1;j<=m;j++){
			scanf("%d",&x);
			if(j==1) add_edge(id[i][1][1],t,x);
			else if(j==m) add_edge(s,id[i][m-1][0],x);
			else add_edge(id[i][j-1][0],id[i][j][1],x);//横线分开(i,j-1)的上半和(i,j)的下半 
		}
	}
	for(int i=1;i<n;i++){
		for(int j=1;j<m;j++){
			scanf("%d",&x);
			add_edge(id[i][j][0],id[i][j][1],x);//斜线分开一个格的两半 
		}
	}
	printf("%d\n",dijkstra(s,t));
}