快速傅里叶变换(FFT)学习笔记(其一)

再探快速傅里叶变换(FFT)学习笔记(其一)

目录

• 再探快速傅里叶变换(FFT)学习笔记(其一)
  • 写在前面
    • 为什么写这篇博客
    • 一些约定
  • 前置知识
    • 多项式卷积
    • 多项式的系数表达式和点值表达式
    • 单位根及其性质
  • DFT和IDFT
    • DFT的过程
    • IDFT的过程
  • FFT
    • FFT的数学证明及时间复杂度分析
    • FFT的递归实现
    • FFT的非递归实现
    • FFT的局限性
  • 例题

写在前面

为什么写这篇博客

笔者去年暑假刚刚学习过FFT,NTT的一些基础应用。但当时对FFT和NTT的理解还不够深入。本博客参考2016年国家集训队论文中雅礼中学毛啸的《再探快速傅立叶变换》,对之前学习时的不足之处做了补充。

为了不使篇幅过长，预计将把学习笔记分为四部分:

1. DFT,IDFT,FFT的定义,实现与证明
2. NTT的实现与证明,任意模数NTT
3. FFT的优化技巧
4. 多项式相关操作

注意:本文为了严谨性可能会牺牲一些可读性

阴晴朝夕态倏忽兮，纷变换乎秋春窈窕缭绕，别有天地兮，莽不知汉与秦之日月。
—— 〔明〕张萱 黄山歌为吴孝父作

一些约定

1. \([p(x)]=\begin{cases}1,p(x)为真 \\ 0,p(x)为假 \end{cases}\)

2. 本文中序列的下标从0开始

3. 若\(s\)是一个序列,\(|s|\)表示\(s\)的长度

4. 若大写字母如\(F(x)\)表示一个多项式,那么对应的小写字母如\(f\)表示多项式的每一项系数，即\(F(x)=\sum_{i=0}^{n-1} f_ix^i\)

5. 用\(DFT(a)\)表示a做DFT后的结果,IDFT同理

前置知识

多项式卷积

多项式\(A(x)=\sum_{i=0}^{n-1} a_ix^i\)(注意最高次项的指数为\(n-1\),至于为什么要这样定义见下文)

定义1.1 对于两个多项式\(A(x)=\sum_{i=0}^{n-1} a_ix_i,B(x)=\sum_{i=0}^{m-1} b_ix_i\),我们定义\(A(x)\)和\(B(x)\)的卷积为:

\[A(x) \cdot B(x)=\sum_{i=0}^{n+m-2} x^i\sum_{k=0}^i a_kb_{i-k} \]

实际上我们只要考虑系数，也就是给出两个序列\(a,b\),求序列\(c\)使得$$c_i=\sum_{k=0}^i a_k b_{i-k} \tag{1.1}$$

直接计算卷积显然是\(O(n^2)\)的,FFT可以用来优化这个过程

多项式的系数表达式和点值表达式

系数表达式就是多项式中每一项的系数\(a_0,a_1 \dots a_{n-1}\)

我们知道,n个点可以确定一个n-1次多项式.那么，一个n-1次多项式\(F(x)\)也可以表示成这样的一个集合\(\{(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)) \dots (x_{n-1},f(x_{n-1}))\}\).比如多项式\(f(x)=x^2+x+1\)就可以表示成\(\{(1,3),(2,7),(-1,1)\}\)

这样有什么用呢?如果已知\(A(x)\)和\(B(x)\)的点值表达式,可以\(O(n)\)计算\(C(x)=A(x)B(x)\)的点值表达式

比如\(A(x)=\{(x_0,A(x_0)),(x_1,A(x_1)),(x_2,A(x_2)),....,(x_n,A(x_n))\}\)

\(B(x)=\{(x_0,B(x_0)),(x_1,B(x_1)),(x_2,B(x_2)),....,(x_n,B(x_n))\}\)

\(C(x)=A(x)\times B(x)=\{(x_0,A(x_0)\times B(x_0)),(x_1,A(x_1)\times B(x_1)),(x_2,A(x_2)\times B(x_2)),....,(x_n,A(x_n)\times B(x_n))\}\)

所以:我们可以在\(O(n)\)的时间内计算出两个点值表达式的乘积,只需要把对应点的\(y\)坐标相乘即可。但是,把系数表达式和点值表达式互相转化仍然需要\(O(n^2)\)时间.(每代入一个\(x\)都需要\(O(n)\)时间计算\(A(x)\))

单位根及其性质

定义1.2:\(n\)次单位根为满足:\(n\)是最小的满足\(\omega^n=1\)的复数\(\omega\)

容易发现,\(n\)次单位根有\(n\)个,他们分布在复平面上的单位圆上。(这里我们只讨论\(n\)为偶数的情况)

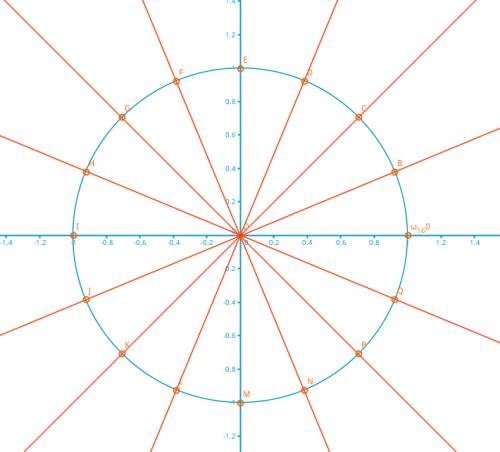
把单位圆\(n\)等分,圆上的每个分割点都对应一个单位根.从点\((1,0)\)开始,逆时针把这\(n\)个点从\(0\)开始编号,第\(k\)个点对应的复数记作\(w_n^k\),上图呈现的就是\(\omega_{16}^0 \text{~} \omega_{16}^{15}\)

容易发现\(\omega_n^k\)的幅角为\(\frac{2k\pi}{n}\).(一整个圆为\(2\pi \ \text{rad}\),分为\(n\)份,再取\(k\)份)，因此，有:

\[\omega_n^k=\cos \frac{2k\pi}{n}+\text{i} \sin \frac{2k\pi}{n} \tag{1.2.1} \]

单位根有如下的性质:

定理1.2.1 \(\forall p \in \mathbb{Z}, \omega_n^k=\omega_{pn}^{pk}\)

代数证明:

\(\omega_{pn}^{pk}=\cos \frac{2pk \pi}{pn}+ \text{i}\sin \frac{2pk\pi}{pn}=\cos \frac{2k\pi}{n}+\text{i} \sin \frac{2k\pi}{n}=\omega_n^k\)

几何证明:单位圆分成\(n\)份，数\(k\)次，和分成\(pn\)份，数\(pk\)次所代表复数是一样的

定理1.2.2 \(\omega_{n}^{k+\frac{n}{2}}=-\omega_{n}^k\)

代数证明:

\[\begin{aligned} \omega_{n}^{k+\frac{n}{2}} &= \cos \frac{2(k+\frac{n}{2}\pi)}{n}+ \text{i} \sin \frac{2(k+\frac{n}{2}\pi)}{n}\\ &=\cos(\frac{2k \pi}{n}+\pi)+\text{i}\sin(\frac{2k \pi}{n}+\pi) \\&= -\cos \frac{2k\pi}{n}-\text{i} \sin \frac{2k\pi}{n}=-\omega_n^k\end{aligned} \]

倒数第二步用到了三角函数的诱导公式

几何证明:

\(\frac{n}{2}\)代表半圈，所以这个式子的意思是从编号为\(k\)的复数开始走半圈，代表的复数和之前的正好相反（实部和虚部都相反）

定理1.2.3 \(\omega_n^p \times \omega_n^q=\omega_n^{p+q}\)

令\(\alpha=\frac{2p\pi}{n},\beta=\frac{2p\pi}{n}\)

则\(\omega_n^p=\cos \alpha+ \text{i} \sin \alpha,\omega_n^q=\cos \beta+ \text{i} \sin \beta\)

\[\begin{aligned} \omega_{n}^{p} \times \omega_{n}^{q}&=(\cos \alpha \cos \beta-\sin \alpha \sin \beta)+i(\sin \alpha \cos \beta+\cos \alpha \sin \beta)\\ &=\cos (\alpha+\beta)+i \sin (\alpha+\beta)\\&=\omega_{n}^{p+q} \end{aligned}\]

证明用到了复数乘法和三角函数的和角公式.注意到定理1.2.2实际上是定理1.2.3的推论，证明留给读者。这个公式极为重要，在FFT的公式推导中会用到。

定理1.2.3的另一个推论，\(\omega_n^k=(\omega_n^1)^k\)

证明显然

定理1.2.4

\[\forall v \in \mathbb{N},\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{v k}=[v \bmod n=0] \]

证明:

当\(v \bmod n =0\)时, \(\omega_{n}^{vk}=\cos\frac{2vk \pi}{n}+\text{i} \sin \frac{2vk \pi}{n}\)

​ 那么\(\frac{vk}{n}\)一定是整数,所以\(\cos\frac{2vk \pi}{n}=1,\sin \frac{2vk \pi}{n}=0,\omega_n^{vk}=1\)

​ 所以\(\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{v k}=\frac{1}{n} \times n =1\)

当\(v \mod n \neq 0\)时,容易发现\(\omega_n^v \neq 1\),

​ 那么上式实际上是一个等比数列,根据等比数列求和公式有:

​ $$\begin{aligned} \frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{v k}&=\frac{1-\omega_n^{{vn}}{n(1-\omega_n}v)} \ &= \frac{1-\omega_1^{v}{n(1-\omega_n}v)}\end{aligned}$$

​ 而\(\omega_1^v=\cos(2v\pi)+i\sin(2v \pi)=1\)

​ 因此\(\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{v k}=0\)

证毕.

这个定理会在IDFT的正确性证明中用到

DFT和IDFT

在上文中我们提到了多项式的系数表达式和点值表达式，并发现点值表达式可以简化卷积运算。

离散傅里叶变换(Discrete Fourier Transform,DFT):是把系数表达式转化为点值表达式的一种算法

逆离散傅里叶变换(Inverse Discrete Fourier Transform,IDFT):是把点值表达式转化为系数表达式的一种算法。

那么求\(A\)和\(B\)的卷积就可以先对\(A\)和\(B\)做DFT,再将\(A\)和\(B\)的点值表达式相乘得到\(C\),最后再对\(C\)做IDFT

DFT的过程

对于多项式\(A,B\),我们找到最小的大于\(|A|+|B|\)的2的整数幂\(n\),至于为什么是2的整数幂后面会提到。给定序列\(a\),对于\(k \notin [0,|a|)\),我们定义\(a_k=0\)

要想得到一个系数表达式的点值表达式，我们可以任意选\(n\)个值代入。但是傅里叶想到,单位根有着特殊的性质，可以把\(n\)次单位根代入多项式。形式化的说,设多项式\(A(x)=\sum_{i=0}^{n-1}a_ix^i\),则\(A(x)\)的DFT变换结果为\(a'_k=A(\omega_n^k)=\sum_{i=0}^{n-1}a_i \omega_n^{ki}\)

我们后面提到的多项式与系数序列的对应关系都类似\(A(x)\)与\(a\)的对应关系，对\(A(x)\)做DFT就是对序列\(a\)做DFT;说一个东西做DFT得到了\(A(x)\),就是得到了序列\(a\)

容易发现DFT的时间复杂度为\(O(n^2)\)

IDFT的过程

代入\(n\)次单位根的作用在IDFT中显现出来.

定理2.1 :把多项式\(A(x)\)的离散傅里叶变换结果\(f(\omega_n^0),f(\omega_n^1) \dots f(\omega_n^{n-1})\)作为另一个多项式\(B(x)\)的系数，取单位根的共轭复数即\(\omega_n^0,\omega_n^{-1},\omega_n^{-2} \dots \omega_n^{-(n-1)}\)作为\(x\)代入\(B(x)\)，得到的每个数再除以\(n\)，得到的是\(A(x)\)的各项系数

也就是说,把点值表达式中点的\(y\)坐标作为另一个多项式的系数后,IDFT的过程和DFT几乎一样,只是代入的是单位根的共轭复数。

我们暂时不证明定理2.1,而是证明一个更强的定理:

定理2.2:把多项式\(A(x)\)的DFT结果\(a\),和\(B(x)\)的DFT结果\(b\)对应相乘,得到序列\(t_i=a_ib_i\);再对\(t_i\)做IDFT,得到的序列就是\(C(x)=A(x)\cdot B(x)\)的各项系数\(c_i\)

证明:

由卷积的定义式\((1.1)\)我们有:

\[c_{r}=\sum_{p, q}[(p+q) \bmod n=r] a_{p} b_{q} \tag{2.1} \]

看到取模想到定理1.1.4

\[\forall v \in \mathbb{N},\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{v k}=[v \bmod n=0] \tag{2.2} \]

故:

\[\begin{aligned} &[(p+q) \bmod n=r] \\ =&[(p+q-r) \bmod n=0] \\ =& \frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{(p+q-r) k} \\ =& \frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{-r k} \omega_n^{p k} \omega_n^{q k} \end{aligned}\]

代入\((2.1)\)

\[\begin{align*} c_{r} &=\sum_{p, q}[(p+q) \bmod n=r] a_{p} b_{q} \\ &=\sum_{p, q} \frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{-r k} \omega_n^{p k} \omega_n^{q k} a_{p} b_{q} \\ &=\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{-r k} \sum_{p, q} \omega_n^{p k} a_{p} \omega_n^{q k} b_{q} \\ &=\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{-r k} \sum_{p} \omega_n^{p k} a_{p} \sum_{q} \omega_n^{q k} b_{q}\tag{2.3} \\&=\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{-r k} a'_k b'_k \\&=\frac{1}{n} \sum_{k=0}^{n-1} \omega_n^{-r k} t_k\end{align*} \]

容易发现定理2.1是定理2.2 的推论,即\(B(x)\)的系数都为1时的情况.式\((2.3)\)实际上指出了DFT和IDFT求卷积的过程。

和DFT类似,IDFT的时间复杂度为\(O(n^2)\)

FFT

上一部分我们提到了DFT的公式，但是这样直接做还是太慢了。因此我们要利用单位根的性质来加速DFT,这个算法被称为快速傅立叶变换(Fast Fourier Transform,FFT). 同样,我们也可以加速IDFT,即IFFT.

这几个算法的关系如下图所示:

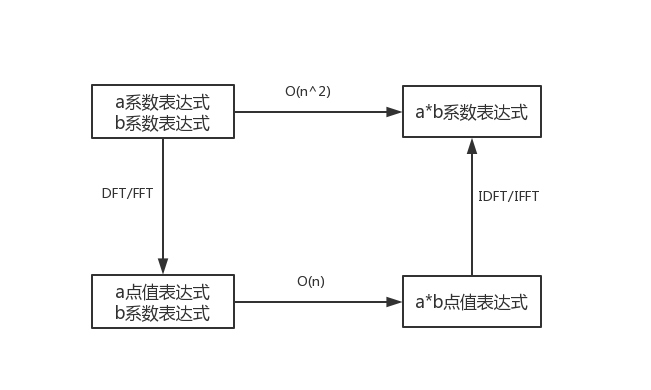
其中FFT,IFFT的时间复杂度均为\(O(n \log n)\)

FFT的数学证明及时间复杂度分析

我们对多项式\(A(x) = a_0 + a_1x + a_2x^2 +...+a_{n-1}x^{n-1}\)进行FFT,仍然把\(\omega_n^k\)代入

把\(a\)按照下标奇偶性分为两部分:

\(A_1(x) = a_0 + a_2x + ... + a_{n - 2}x^{\frac{n}{2} - 1}\)

\(A_2(x) = a_1 + a_3x + ... + a_{n - 1}x^{\frac{n}{2} - 1}\)

那么我们有:

\(A(x) = A_1(x^2) + xA_2(x^2)\)

将\(x=\omega_n^k\)代入,

对于\(k < \frac{n}{2}\)(根据先前的定义,n为2的次幂,所以没有取整问题)

\[\begin{align*} A(\omega_n^k) &= A_1(\omega_n^{2k}) + \omega_n^kA_2(\omega_n^{2k}) \\ &= A_1(\omega_{\frac{n}{2}}^{k}) + \omega_n^kA_2(\omega_{\frac{n}{2}}^{k}) \tag{3.1}\end{align*} \]

​ 证明用到了定理1.2.1:\(\forall p \in \mathbb{Z}, \omega_n^k=\omega_{pn}^{pk}\)

对于剩下的部分,即\(\omega_{n}^{k+\frac{n}{2}}(k<\frac{n}{2})\)

\[\begin{align*} A(\omega_n^{k + \frac{n}{2}}) &= A_1(\omega_n^{2k + n}) + \omega_n^{k + \frac{n}{2}}A_2(\omega_n^{2k + n}) \\ &= A_1(\omega_{\frac{n}{2}}^{k} \times \omega_n^n) + \omega_n^{k + \frac{n}{2}} A_2(\omega_{\frac{n}{2}}^{k} \times \omega_n^n) \\ &= A_1(\omega_{\frac{n}{2}}^{k}) - \omega_n^kA_2(\omega_{\frac{n}{2}}^{k}) \tag{3.2} \end{align*} \]

证明用到了定理1.2.1和定理1.2.3:\(\omega_n^p \times \omega_n^q=\omega_n^{p+q}\)

式\((3.1),(3.2)\)也被称为“蝴蝶操作”, 通过蝴蝶操作,我们只要知道两个多项式\(A_1(x),A_2(x)\)在\((\omega_{\frac{n}{2}}^{0}, \omega_{\frac{n}{2}}^{1}, \omega_{\frac{n}{2}}^{2}, ... , \omega_{\frac{n}{2}}^{\frac{n}{2} - 1})\)处的点值表达式,就可以求出\(A(x)\)在\((\omega_n^0, \omega_n^1, \omega_n^2, ..., \omega_n^{n-1})\)处的点值表达式了了。每次递归下去规模缩小一半,\(n=1\)时终止.由于长度\(n\)每次除2,且要求每次的\(n\)均为偶数，所以我们需要\(n\)是2的正整数次幂

设给长度为\(n\)的序列做\(FFT\)的时间为\(T(n)\),那么我们有

\[T(n)=2T(\frac{n}{2})+n \]

根据主定理,\(T(n)=\Theta(n \log n)\)

FFT的递归实现

FFT递归实现很好理解.注意可以使用C++自带的复数类<complex>,也可以自己手写复数类。

<complex>重载了+,-,*,/,=,==等运算符，在使用上很方便，几乎和操作整型变量没有区别。两个成员函数.real(),.imag()分别返回复数的实部和虚部。更多它的用法请参考这个链接

#include<complex>//c++自带复数类
const double pi=acos(-1.0);
typedef complex<double> com;
com a[maxn+5],b[maxn+5],c[maxn+5];
void fft(com *x,int n,int type){//orz Fourier 
	if(n==1) return;//递归边界
	com l[n>>1],r[n>>1];
	for(int i=0;i<n;i++){//按奇偶分类
		if(!(i&1)) l[i>>1]=x[i]; 
		else r[i>>1]=x[i];
	}
	fft(l,n>>1,type);//递归对n/2的长度做FFT
	fft(r,n>>1,type);
	
	com wn1=com(cos(2*pi/n),type*sin(2*pi/n))/*w_n^0*/,wnk=com(1,0);	
	for(int i=0;i<(n>>1);i++){
		x[i]=l[i]+wnk*r[i];//式(3.1)
		x[i+(n>>1)]=l[i]-wnk*r[i];//式(3.2)
		wnk*=wn1;//递推算w_n^k
	}
}
int main(){
     //....
     int m=n*2;//这个数根据题目算要求来定,这里是长度为n的两个序列卷积,那就取2n
	 n=1;
	 while(n<m) n*=2;//计算出最小的2的次幂
	 fft(a,n,1);
	 fft(b,n,1);
	 for(int i=0;i<n;i++) c[i]=a[i]*b[i];
	 fft(c,n,-1);
     for(int i=0;i<m;i++) printf("%lf ",c[i].real()/n);//记得除n
    //....
}

FFT的非递归实现

很遗憾,FFT的递归实现常数极大(虽然非递归实现常数也很大),几乎无法通过任何OI中FFT的题目。

我们观察递归过程中根据奇偶改变系数位置的方式,例如长度为8的情况:

\[\begin{aligned} &\left(a_{0}, a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, a_{7}\right)\\ &\left(a_{0}, a_{2}, a_{4}, a_{6}\right)\left(a_{1}, a_{3}, a_{5}, a_{7}\right)\\ &\left(a_{0}, a_{4}\right)\left(a_{2}, a_{6}\right)\left(a_{1}, a_{5}\right)\left(a_{3}, a_{7}\right)\\ &\left(a_{0}\right)\left(a_{4}\right)\left(a_{2}\right)\left(a_{6}\right)\left(a_{1}\right)\left(a_{5}\right)\left(a_{3}\right)\left(a_{7}\right) \end{aligned}\]

观察\(0,4,2,6,1,5,3,7\)的二进制表示\(000,100,010,110,001,101,011,111\)，

比较\(0,1,2,3,4,5,6,7\)的二进制表示\(000,001,010,011,100,101,110,111\)

我们发现,初始时位置\(x\)上的数会被交换到x二进制位翻转后的位置,记为\(rev(x)\)。注意这里的反转指的是反过来写,而不是每一位交换01。这种操作也被称为“位逆序置换”。那么只要处理出这个序列,每次FFT的都是一段连续的区间,可以非递归求解。

\(rev(x)\)可以根据如下代码递推求出

for(int i=0;i<n;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));

证明: 对于数\(i\),我们已经求出\(i>>1\)的置换结果,如\(k=5,i=(10111)_2,i>>1=(1011)_2\);那么我们先反转从左到右前\(k-1\)位,即\(rev[i>>1]=rev[(01011)_2]=(11010)_2\),右移一位去掉前导0(翻转后到了末尾)就得到了前\(k-1\)位反转的结果; 然后再加上最后一位,最后一位的值是\((i\text{&}1)\),要左移到最前面.

int rev[maxn+5];//数x位逆序置换后变成rev[x]
int n,k;//n=2^k
void fft(com *x,int n,int type){//type=1做FFT,type=-1做IFFT
    for(int i=0;i<n;i++) if(i<rev[i]) swap(x[i],x[rev[i]]);//做置换,i<rev[i]防止一个数被换两次换回原位
    for(int len=1;len<n;len*=2){
        int sz=len*2;//当前处理的长度为len*2,len=1的情况不用计算,就是x[i]
        com wn1=com(cos(2*pi/sz),sin(2*pi/sz)*type);//计算n次单位根w_n^1,type=-1时得到共轭复数
        for(int l=0;l<n;l+=sz){//枚举一对长度为len的区间，对这两个区间做蝴蝶操作
            int r=l+len-1;//[l,l+len-1]为前半段,[l+len,r]为后半段
            com wnk=1;
            for(int i=l;i<=r;i++){
                com tmp=x[i+len];//用tmp临时存储值
                x[i+len]=x[i]-wnk*tmp;//式(3.1)
                x[i]=x[i]+wnk*tmp;//式(3.2)
                wnk*=wn1;//递推计算w_n^k
            }
        }
    }
    if(type==-1) for(int i=0;i<n;i++) x[i]/=n;//IFFT记得除n
}
int main(){
    n=1,k=0;
	while(n<m){
        n*=2;
        k++;
    }//预处理n,k
    for(int i=0;i<n;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));//预处理rev
    fft(a,n,1);
    fft(b,n,1);
    for(int i=0;i<n;i++) ans[i]=a[i]*b[i];
    fft(ans,n,-1);
}

FFT的局限性

显然FFT的过程中会出现浮点数的精度误差。比如在递推单位根\(w_n^k=w_n^{k-1}\times w_n^1\)时的精度误差比较大， 但一般可以接受。如果追求更高精度，可以对于每个\(k\)重新计算\(\omega_n^k=\cos \frac{2k\pi}{n}+\text{i} \sin \frac{2k\pi}{n}\),但时间开销较大。

如果有取模运算，可以使用第二节中提到的NTT算法

另外，在第三节中，我们会介绍减少FFT常数的几种方法，以及对任意长度的序列做DFT的方法。

例题

[1.BZOJ 3527] [ZJOI2014]力(FFT)

2.[Codeforces 580D]Fizzy Search(FFT)