[Codeforces 1295D]Same GCDs(欧拉函数或分解质因数+容斥原理)

[Codeforces 1295D]Same GCDs(欧拉函数+分解质因数)

题面

已知正整数\(a,m\),求有多少个正整数\(x\)满足\(0 \leq x <m\)且\(\gcd(a,m)=\gcd(a+x,m)\)

\(a,m \leq 10^{10}\)

分析

令\(\gcd(a,m)=g\)

我们要求的其实是\(\sum_{i=a}^{a+m-1} [gcd(i,m)=g]\)

法一(分解质因数+容斥原理):

\[\begin{aligned} \sum_{i=a}^{a+m-1} [gcd(i,m)=g]&= \sum_{i=a}^{a+m-1}[gcd(\frac{i}{g},\frac{m}{g})=1] \\ &=\sum_{i=\frac{a}{g}}^{\frac{a+m-1}{g} }[gcd(i,\frac{m}{g})=1] \end{aligned} \]

问题转化成求区间\([l,r]\)中与\(x\)互质的数的个数。差分一下变成区间\([1,r]\)中与\(x\)互质的数的个数。

先把\(x\)分解质因数,枚举质因数集合\(S\),那么能被S中所有数整除的数的个数就是\(\frac{r}{\prod_{p \in S}p}\). 减去这些就是互质的数的个数，但是这样可能会算重，所以还要容斥。答案为

\[f(x,r)=r-\sum (-1)^{|S|-1}\frac{r}{\prod_{p \in S}p} \]

最终答案为\(f(\frac{m}{g},\frac{a+m-1}{g})-f(\frac{m}{g},\frac{a}{g}-1)\)

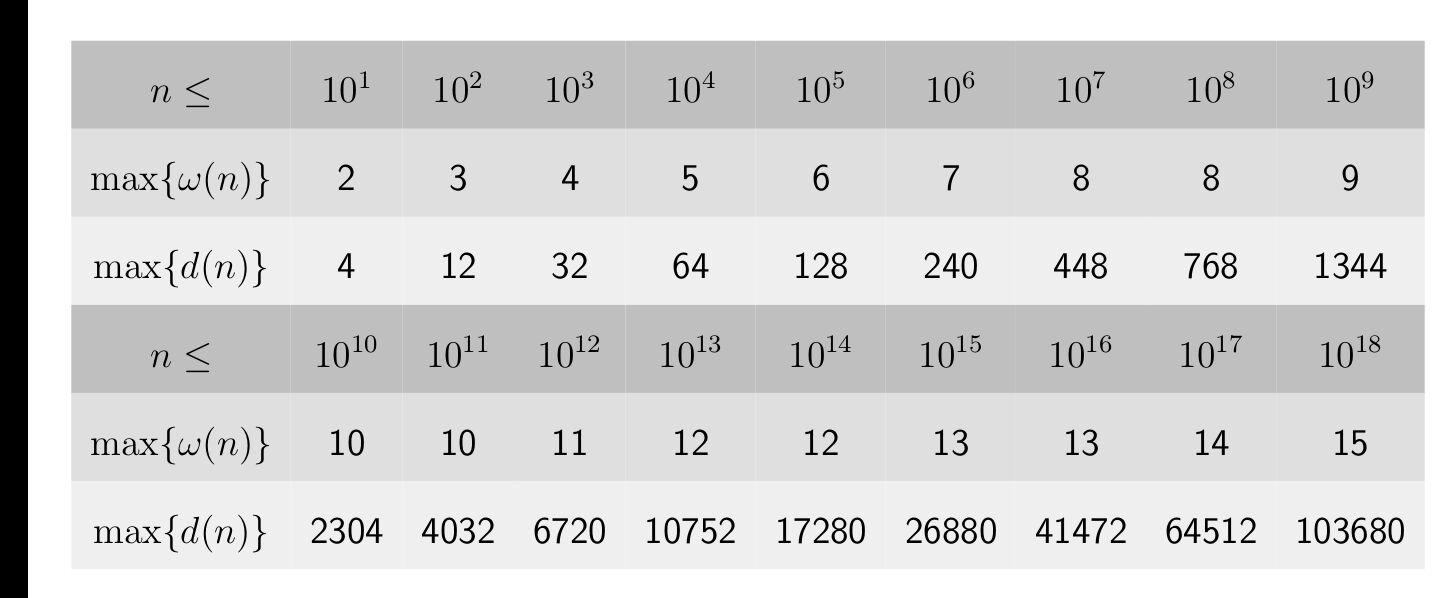
时间复杂度\(O(\sqrt{a}+2^{\omega(a)})\),其中\(\omega(a)\)为\(a\)本质不同的质因子个数,查表得出大约在10左右

法二(欧拉函数):

根据辗转相除法

\[\begin{aligned}\sum_{x = 0}^{m - 1} [\gcd(a, m) = \gcd(a + x, m)]&=\sum_{x = 0}^{m - 1} [\gcd(a, m) = \gcd((a + x) \bmod m, m)] \end{aligned} \]

\((a+x) \bmod m\)只是把\(x\)的区间平移,范围还是\([0,m]\)

故

\[\begin{aligned}原式&=\sum_{x = 0}^{m - 1} [\gcd(a, m) = \gcd((a + x) \bmod m, m)] \\ &= \sum_{i = 0}^{m-1} [\gcd(i, m) = g] \\ &= \sum_{i = 1}^{m} [\gcd(i, m) = g]\\ &=\sum_{i=1}^{\frac{m}{g}} [gcd(i,\frac{m}{g})=1] \\&= \varphi(\frac{m}{g}) \end{aligned} \]

时间复杂度\(O(\sqrt{a})\)

某不存在的法三

显然可以莫比乌斯反演。但是CF2D级别的题有点大材小用了

代码

法一

#include<iostream>
#include<cstdio>
#include<cstring> 
#include<vector>
using namespace std;
typedef long long ll;
 
ll a,m;
inline ll gcd(ll a,ll b){
	return b==0?a:gcd(b,a%b);
}
 
ll solve(ll x,ll n){
	vector<ll>p;
	p.clear();
	for(ll i=2;i*i<=x;i++){
		if(x%i==0){
			p.push_back(i);
			while(x%i==0) x=x/i;
		}
	}
	if(x>1) p.push_back(x);
	ll sum=0;
	for(ll i=1;i<(1<<p.size());i++){
		int cnt1=0;
		ll fac=1; 
		for(ll j=0;j<p.size();j++){
			if(i&(1<<j)){
				cnt1++;
				fac*=p[j];
			} 
		}
		if(cnt1%2==1) sum+=n/fac;
		else sum-=n/fac;
	}
	return n-sum;
}
 
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%I64d %I64d",&a,&m);
		ll g=gcd(a,m);
		printf("%I64d\n",solve(m/g,(a+m-1)/g)-solve(m/g,a/g-1));
	}
}

法二:

#include<iostream>
#include<cstdio>
#include<cstring> 
#include<vector>
using namespace std;
typedef long long ll;
 
ll a,m;
inline ll gcd(ll a,ll b){
	return b==0?a:gcd(b,a%b);
}
ll phi(ll x){
	ll ans=x;
	for(ll i=2;i*i<=x;i++){
		if(x%i==0){
			ans=ans/i*(i-1); 
			while(x%i==0) x=x/i;
		}
	}
	if(x>1) ans=ans/x*(x-1);
	return ans;
}
 
 
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%I64d %I64d",&a,&m);
		ll g=gcd(a,m);
		printf("%I64d\n",phi(m/g));
	}
}