[BZOJ1576] [BZOJ3694] [USACO2009Jan] 安全路径(最短路径+树链剖分)

[BZOJ1576] [BZOJ3694] [USACO2009Jan] 安全路径(最短路径+树链剖分)

题面

BZOJ1576和BZOJ3694几乎一模一样，只是BZOJ3694直接给出了最短路树

给出一个n个点m条边的无向图，n个点的编号从1~n，定义源点为1。定义最短路树如下：从源点1经过边集T到任意一点i有且仅有一条路径，且这条路径是整个图1到i的最短路径，边集T构成最短路树。 给出最短路树，求对于除了源点1外的每个点i，求最短路，要求不经过给出的最短路树上的1到i的路径的最后一条边。

分析

求最短路树的过程略。

删掉了树上一个点i到父亲的边(即1到i路径上最后一条边)后,我们必须经过非树边才能到达i。贪心考虑，只经过一条非树边显然是最优的。

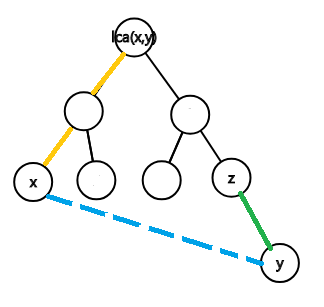
对于一条非树边(x,y) [图中蓝色虚线],它在树上对应一条路径(x,y).对于这条路径上的点z,在z往它父亲的边被删除后，我们可以走这样的路径1->x->y->z。1->x的距离显然为\(dist(x)\),x->y的距离为\(len(x,y)\),y->z的距离[绿线]是\(dist[y]-dist[z]\).因此到z的路径长度就是\(dist[x]+dist[y]+len(x,y)-dist[z]\)

注意到当z=lca(x,y)时，是不能从1->x->y->z的，因为z到父亲的边被删除后无法到达x.

那么方法就很明确了。对于每条边，我们用\(dist[x]+dist[y]+len(x,y)\)去更新路径(x,y)(不包含lca)上的点，每个点\(z\)求出\(min(dist[x]+dist[y]+len(x,y))\)。最后输出\(min(dist[x]+dist[y]+len(x,y))-dist[z]\)即可。路径修改，单点查询，可以用树链剖分解决。时间复杂度\(O(n \log^2 n)\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#define maxn 4000
#define maxm 100000 
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;

int n,m;
struct edge{
	int from;
	int to;
	int next;
	int len;
	int type;
}E[maxm*2+5];
int head[maxn+5];
int esz=1;
void add_edge(int u,int v,int w,int t){
	esz++;
	E[esz].from=u;
	E[esz].to=v;
	E[esz].next=head[u];
	E[esz].len=w;
	E[esz].type=t;
	head[u]=esz;
}

struct node{
	int id;
	ll dist;
	node(){
		
	}
	node(int _id,ll _dist){
		id=_id;
		dist=_dist;
	}
	friend bool operator < (node p,node q){
		return p.dist>q.dist;
	}
};
bool vis[maxn+5];
ll dist[maxn+5];
void dijkstra(int s){
	priority_queue<node>q;
	memset(vis,0,sizeof(vis));
	memset(dist,0x3f,sizeof(dist));
	dist[s]=0;
	q.push(node(s,0));
	while(!q.empty()){
		int x=q.top().id;
		q.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=head[x];i;i=E[i].next){
			int y=E[i].to;
			if(dist[y]>dist[x]+E[i].len){
				dist[y]=dist[x]+E[i].len;
				if(!vis[y]) q.push(node(y,dist[y]));
			}
		}
	}
}

vector<int>T[maxn+5];
int deep[maxn+5];
int sz[maxn+5];
int fa[maxn+5];
int son[maxn+5];
int top[maxn+5];
int dfn[maxn+5];
int tim;
void dfs1(int x,int f){
	sz[x]=1;
	fa[x]=f;
	deep[x]=deep[f]+1;
	for(int i=0;i<T[x].size();i++){
		int y=T[x][i];
		if(y!=f){
			dfs1(y,x);
			sz[x]+=sz[y];
			if(sz[y]>sz[son[x]]) son[x]=y;
		}
	}
}
void dfs2(int x,int t){
	top[x]=t;
	dfn[x]=++tim;
	if(son[x]) dfs2(son[x],t);
	for(int i=0;i<T[x].size();i++){
		int y=T[x][i];
		if(y!=fa[x]&&y!=son[x]){
			dfs2(y,y);
		}
	}
}

struct segment_tree{
	struct node{
		int l;
		int r;
		ll val;
		ll mark;
	}tree[maxn*4+5];
	void push_up(int pos){
		tree[pos].val=max(tree[pos<<1].val,tree[pos<<1|1].val);
	}
	void build(int l,int r,int pos){
		tree[pos].l=l;
		tree[pos].r=r;
		tree[pos].mark=INF;
		tree[pos].val=INF;
		if(l==r) return;
		int mid=(l+r)>>1;
		build(l,mid,pos<<1);
		build(mid+1,r,pos<<1|1);
		push_up(pos);
	}
	void push_down(int pos){
		if(tree[pos].mark!=INF){
			tree[pos<<1].mark=min(tree[pos<<1].mark,tree[pos].mark);
			tree[pos<<1|1].mark=min(tree[pos<<1|1].mark,tree[pos].mark);
			tree[pos<<1].val=min(tree[pos<<1].val,tree[pos].mark);
			tree[pos<<1|1].val=min(tree[pos<<1|1].val,tree[pos].mark);
			tree[pos].mark=INF;
		}
	} 
	void update(int L,int R,ll uval,int pos){
		if(L<=tree[pos].l&&R>=tree[pos].r){
			tree[pos].mark=min(tree[pos].mark,uval);
			tree[pos].val=min(tree[pos].val,uval);
			return;
		}
		push_down(pos);
		int mid=(tree[pos].l+tree[pos].r)>>1;
		if(L<=mid) update(L,R,uval,pos<<1);
		if(R>mid) update(L,R,uval,pos<<1|1);
		push_up(pos);
	}
	ll query(int L,int R,int pos){
		if(L<=tree[pos].l&&R>=tree[pos].r){
			return tree[pos].val;
		}
		push_down(pos);
		int mid=(tree[pos].l+tree[pos].r)>>1;
		ll ans=INF;
		if(L<=mid) ans=min(ans,query(L,R,pos<<1));
		if(R>mid) ans=min(ans,query(L,R,pos<<1|1));
		return ans;
	}
}S;

int lca(int x,int y){
	while(top[x]!=top[y]){
		if(deep[top[x]]<deep[top[y]]) swap(x,y);
		x=fa[top[x]];
	}
	if(deep[x]>deep[y]) swap(x,y);
	return x;
}
void update(int x,int y,ll val){
//	printf("update %d->%d val=%d\n",x,y,val);
	int tx=top[x],ty=top[y];
	while(tx!=ty){
		if(deep[tx]<deep[ty]){
			swap(tx,ty);
			swap(x,y);
		}
		S.update(dfn[tx],dfn[x],val,1);
		x=fa[tx];
		tx=top[x];
	}
	if(deep[x]>deep[y]) swap(x,y);
	S.update(dfn[son[x]],dfn[y],val,1);//注意是son[x]而不是x，因为不包含lca
}

int main(){
	int u,v,w,t;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d %d %d %d",&u,&v,&w,&t);
		add_edge(u,v,w,t);
		add_edge(v,u,w,t);
		if(t==1){
			T[u].push_back(v);
			T[v].push_back(u);
		}
	}
	dijkstra(1);
	dfs1(1,0);
	dfs2(1,0);
	S.build(1,n,1); 
	for(int i=2;i<=esz;i+=2){
		if(E[i].type==0){
			int x=E[i].from;
			int y=E[i].to;
			update(x,y,dist[x]+dist[y]+E[i].len);
		}
	}
	for(int i=2;i<=n;i++){
		ll ans=S.query(dfn[i],dfn[i],1);
		if(ans==INF) printf("-1 ");
		else printf("%lld ",ans-dist[i]);
	}
}