[BZOJ 2989]数列(CDQ 分治+曼哈顿距离与切比雪夫距离的转化)
[BZOJ 2989]数列(CDQ 分治)
题面
给定一个长度为n的正整数数列a[i]。
定义2个位置的graze值为两者位置差与数值差的和,即graze(x,y)=|x-y|+|a[x]-a[y]|。
2种操作(k都是正整数):
1.Modify x k:将第x个数的值修改为k。
2.Query x k:询问有几个i满足graze(x,i)<=k。因为可持久化数据结构的流行,询问仅要考虑当前数列,还要考虑任意历史版本,即统计任意位置上出现过的任意数值与当前的a[x]的graze值<=k的对数。(某位置多次修改为同样的数值,按多次统计)
分析
据说正解是二进制分组+主席树?
观察到\(|x-y|+|a[x]-a[y]|\),我们想到曼哈顿距离。于是我们把(x,a[x])看作一个二维平面上的点,而查询的是到平面上一定点距离<=k的点的个数。同时这样还避免了可持久化的问题,因为把a[x]修改成k,相当于新建了一个点。
到平面上一定点曼哈顿距离=k的点的集合(曼哈顿距离下的圆)是一个斜45°,边长为\(\frac{\sqrt{2}}{2}k\)的正方形。我们求的答案就是这个正方形里的点的个数
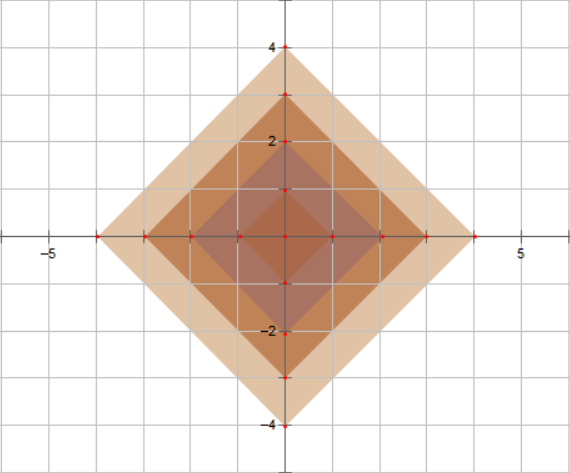
[图片转载自https://www.cnblogs.com/SGCollin/p/9636955.html]
这样的点距离不太好求。但是我们知道切比雪夫距离下的圆是一个四边都平行坐标轴的正方形。因此我们可以把曼哈顿距离转成对应的切比雪夫距离。注:\((x_1,y_1)和(x_2,y_2)的切比雪夫距离是max(|x_1-x_2|,|y_1-y_2|)\)
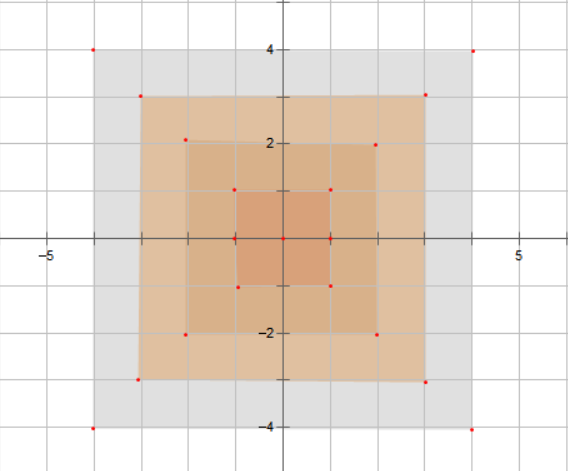
考虑把两个点转化成\((x_1+y_1,x_1-y_1),(x_2+y_2,x_2-y_2)\),容易发现新点的切比雪夫距离和原来点的曼哈顿距离相同.
那么我们只要把询问和修改的每个点都转成(x+y,x-y)的形式,然后问题就变成在把原来查询的正方形转换后新的正方形里点的个数。由于边都平行于坐标轴,这是一个经典的三维偏序问题,详情可参考[BZOJ 2683] 简单题 (CDQ分治)
代码
//首先把询问转成曼哈顿距离,(i,a[i])看成一个点
//注意到曼哈顿距离下的圆为斜45度正方形,圆内点的个数即为答案
//斜的正方形不好查询,考虑切比雪夫距离下的圆为平行于坐标轴的正方形 (相当于逆时针旋转45度)
//把正方形角上的点以及更新的点曼哈顿距离下的坐标转成切比雪夫距离下的坐标
//再在新正方形里二维前缀和即可
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 1000000
using namespace std;
int n,m,tim,cnt,qcnt;
int xx[maxn+5],yy[maxn+5];
inline void change(int& x,int& y){//改变坐标系
int xx=x,yy=y;
x=xx+yy;
y=xx-yy;
}
struct node{
int a;
int b;
int c;
int type;
int val;
int id;
int ans;
node(){
}
node(int _a,int _b,int _c,int _type){
a=_a;
b=_b;
c=_c;
type=_type;
}
node(int _a,int _b,int _c,int _type,int _val,int _id){
a=_a;
b=_b;
c=_c;
type=_type;
val=_val;
id=_id;
ans=0;
}
}q[maxn+5];
int cmpa(node p,node q){
if(p.a==q.a){
if(p.b==q.b) return p.c<q.c;
else return p.b<q.b;
}else return p.a<q.a;
}
int cmpb(node p,node q){
if(p.b==q.b) return p.c<q.c;
else return p.b<q.b;
}
struct fenwick_tree{
int c[maxn+5];
inline int lowbit(int x){
return x&(-x);
}
inline void update(int pos,int val){
for(int i=pos;i<=tim;i+=lowbit(i)) c[i]+=val;
}
inline int query(int pos){
int ans=0;
for(int i=pos;i>0;i-=lowbit(i)) ans+=c[i];
return ans;
}
}T;
node tmp[maxn+5];
void cdq_divide(int l,int r){//orz cdq
if(l==r) return;
int mid=(l+r)>>1;
cdq_divide(l,mid);
cdq_divide(mid+1,r);
int ptr=l-1;
for(int i=mid+1;i<=r;i++){
while(ptr<mid&&q[ptr+1].b<=q[i].b){
ptr++;
if(q[ptr].type==1) T.update(q[ptr].c,1);
}
if(q[i].type==2) q[i].ans+=T.query(q[i].c);
}
for(int i=l;i<=ptr;i++) if(q[i].type==1) T.update(q[i].c,-1);
int num=l-1;
int pl=l,pr=mid+1;
while(pl<=mid&&pr<=r){
if(cmpb(q[pl],q[pr])) tmp[++num]=q[pl++];
else tmp[++num]=q[pr++];
}
while(pl<=mid) tmp[++num]=q[pl++];
while(pr<=r) tmp[++num]=q[pr++];
for(int i=l;i<=r;i++) q[i]=tmp[i];
}
char cmd[10];
int ans[maxn+5];
int main(){
int p,k;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
xx[i]=i;
scanf("%d",&yy[i]);
tim++;
q[++cnt]=node(xx[i]+yy[i],xx[i]-yy[i],tim,1);
}
for(int i=1;i<=m;i++){
scanf("%s",cmd);
if(cmd[0]=='M'){
scanf("%d %d",&p,&k);
tim++;
yy[p]=k;
q[++cnt]=node(xx[p]+yy[p],xx[p]-yy[p],tim,1);
}else{
int x1,y1,x2,y2;
scanf("%d %d",&p,&k);
x1=xx[p]-k;
y1=yy[p];
x2=xx[p]+k;
y2=yy[p];
change(x1,y1);
change(x2,y2);
tim++;
qcnt++;
q[++cnt]=node(x2,y2,tim,2,1,qcnt);
q[++cnt]=node(x1-1,y2,tim,2,-1,qcnt);
q[++cnt]=node(x2,y1-1,tim,2,-1,qcnt);
q[++cnt]=node(x1-1,y1-1,tim,2,1,qcnt);
}
}
sort(q+1,q+1+cnt,cmpa);
cdq_divide(1,cnt);
for(int i=1;i<=cnt;i++){
if(q[i].type==2) ans[q[i].id]+=q[i].val*q[i].ans;
}
for(int i=1;i<=qcnt;i++) printf("%d\n",ans[i]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号