BZOJ1185[HNOI2007] 最小矩形覆盖（旋转卡壳）

BZOJ1185[HNOI2007] 最小矩形覆盖

题面

给定一些点的坐标,要求求能够覆盖所有点的最小面积的矩形,输出所求矩形的面积和四个顶点的坐标

分析

首先可以先求凸包，因为覆盖了凸包上的顶点，凸包内的顶点也一定能被覆盖

结论：这个矩形的一条边一定与凸包的一条边重合。

然后对于凸包的每一条边\(\vec{s_is_{i+1}}\),我们通过旋转卡壳找到最左侧的点l,最右侧的点r,最高点p,过p做\(\vec{s_is_{i+1}}\)的平行线，过l,r做\(\vec{s_is_{i+1}}\)的垂线，就得到了我们要求的矩形

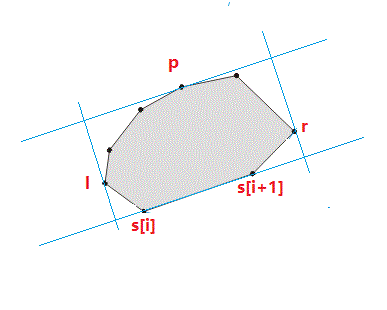
求最大高度的点用叉积最大，最右侧点用点积最大，最左侧点用点积最小（点积为负）

求坐标，可以先根据前面的点积和叉积求出投影长度，再求出边对应的单位向量，乘上长度再相加就得到了点的坐标。如l的坐标就是$s_i+ \frac{\vec{s_is_{i+1}} \cdot \vec{s_il}{}}{|\vec{s_is_{i+1}}|} \frac{ \vec{s_is_{i+1}} }{|\vec{s_is_{i+1}}|} $,另两个端点只需要向量旋转90度即可

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define maxn 100000
#define eps 1e-10
#define INF 1e20
using namespace std;
int n;
struct Vector{
    double x;
    double y;
    Vector(){

    }
    Vector(double _x,double _y){
        x=_x;
        y=_y;
    }
    friend Vector operator + (Vector p,Vector q){
        return Vector(p.x+q.x,p.y+q.y);
    }
    friend Vector operator - (Vector p,Vector q){
        return Vector(p.x-q.x,p.y-q.y);
    }
    friend Vector operator * (Vector a,double d){
    	return Vector(a.x*d,a.y*d);
	}
	friend Vector operator / (Vector a,double d){
		return Vector(a.x/d,a.y/d);
	}
};
typedef Vector point;
inline double dot(Vector p,Vector q){
    return p.x*q.x+p.y*q.y;
}
inline double dist(point p,point q){
    return sqrt(dot(p-q,p-q));
}
inline double cross(Vector p,Vector q){
    return p.x*q.y-p.y*q.x;
}
inline double length(Vector x){
	return sqrt(dot(x,x));
} 
point a[maxn+5];

point O;
int cmp(point P,point Q){
	double ang=cross(P-O,Q-O);
	if(fabs(ang)<eps) return dist(O,P)<dist(O,Q);
	else return ang>eps; 
} 

int top=0;
point s[maxn+5];
void Graham(){
    for(int i=1;i<=n;i++){
        if(a[i].x<a[1].x||(a[i].x==a[1].x&&a[i].y<=a[1].y)) swap(a[i],a[1]);
    }
    O=a[1];
    sort(a+2,a+1+n,cmp);
    for(int i=1;i<=n;i++){
        while(top>1&&cross(s[top]-s[top-1],a[i]-s[top-1])<=eps) top--;//在逆时针方向，叉积<0 
        s[++top]=a[i];
    }
//#ifdef DEBUG
//	for(int i=1;i<=top;i++){
//		printf("(%.5f,%.5f)\n",s[i].x,s[i].y);
//	}
//#endif
}


inline int nex(int x){
	return x%top+1;
}
inline Vector rotate90(Vector p){//把向量逆时针旋转90度 
	//(xcos(a)-ysin(a),xsin(a)+ycos(a))  a=pi/2
	return Vector(-p.y,p.x);
}

point res[10];
double ans=INF;
void Spin(){
	s[top+1]=s[1];
	int l,r,p;
	l=r=p=2;
	for(int i=1;i<=top;i++){
		double D=length(s[i+1]-s[i]);
		while(cross(s[i+1]-s[i],s[p+1]-s[i])-cross(s[i+1]-s[i],s[p]-s[i])>-eps) p=nex(p);
		while(dot(s[r+1]-s[i],s[i+1]-s[i])-dot(s[r]-s[i],s[i+1]-s[i])>-eps) r=nex(r);
		if(i==1) l=r;
		while(dot(s[l+1]-s[i],s[i+1]-s[i])-dot(s[l]-s[i],s[i+1]-s[i])<eps) l=nex(l);
		 //在左侧的时候点积为负数，最小 
		double lenl=dot(s[l]-s[i],s[i+1]-s[i])/D;
		double lenr=dot(s[r]-s[i],s[i+1]-s[i])/D;
		double height=cross(s[i+1]-s[i],s[p]-s[i])/D;
		double area=(fabs(lenr)+fabs(lenl))*fabs(height);//lenl,lenr是有方向的
		if(area<ans){
//			printf("(%.3f %.3f) ",(double)s[i].x,(double)s[i].y); 
//        	printf("(%.3f %.3f)\n",(double)s[i+1].x,(double)s[i+1].y); 
//			printf("S=%.4f l=%d r=%d p=%d\n",area,l,r,p);
			ans=area;
			res[1]=s[i]+(s[i+1]-s[i])/D*lenl;
			res[2]=s[i]+(s[i+1]-s[i])/D*lenr;
			res[3]=res[1]+rotate90((s[i+1]-s[i])/D)*height;
			res[4]=res[2]+rotate90((s[i+1]-s[i])/D)*height;
		}
	}
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%lf %lf",&a[i].x,&a[i].y);
	}
	Graham();
	Spin();
	for(int i=1;i<=4;i++){
		if(res[i].y<res[1].y||(res[i].y==res[1].y&&res[i].x<res[1].x)) swap(res[1],res[i]);
	} 
	O=res[1];
	sort(res+2,res+1+4,cmp);
	for(int i=1;i<=4;i++){
		if(fabs(res[i].x)<eps) res[i].x=0;
		if(fabs(res[i].y)<eps) res[i].y=0;
	}
	printf("%.5f\n",ans);
	for(int i=1;i<=4;i++){
		printf("%.5f %.5f\n",res[i].x,res[i].y);
	}
}