[BZOJ2829] 信用卡 (凸包)

[BZOJ2829] 信用卡 (凸包)

题面

信用卡是一个矩形，唯四个角做了圆滑处理，使他们都是与矩形两边相切的1/4园，如下图所示，现在平面上有一些规格相同的信用卡，试求其凸包的周长。注意凸包未必是多边形，因为他有可能包含若干段圆弧。

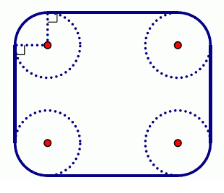
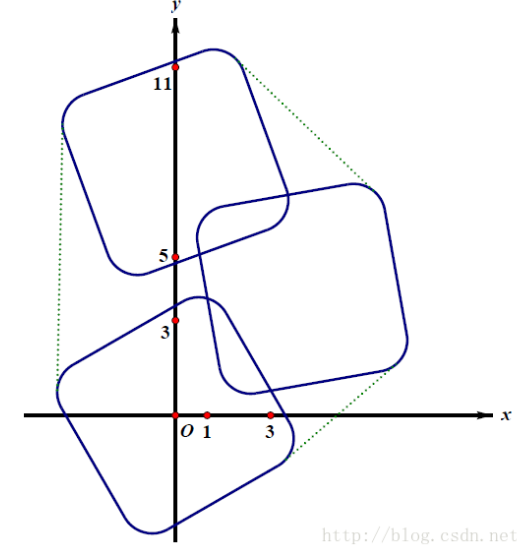
分析

我们发现凸包的圆弧段可以缩成一个圆，然后将直线段向内平移，就可以组成一个多边形

因此对每个卡的四个圆心跑凸包,答案为凸包周长+一个圆的周长

注意四个圆心的计算要用到向量旋转，向量\((x,y)\)逆时针旋转\(\alpha\)（弧度）之后会变成\((x\cos \alpha-y \sin \alpha,x \sin \alpha+y \cos \alpha)\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define eps 1e-6
#define maxn 10000 
using namespace std;
int n; 
const double PI=acos(-1.0);
struct Vector{
	double x;
	double y;
	Vector(){
		
	}
	Vector(double _x,double _y){
		x=_x;
		y=_y;
	}
	friend Vector operator + (Vector p,Vector q){
		return Vector(p.x+q.x,p.y+q.y);
	}
	friend Vector operator - (Vector p,Vector q){
		return Vector(p.x-q.x,p.y-q.y);
	}
	friend bool operator < (Vector p,Vector q){
		if(p.x==q.x) return p.y<q.y;
		else return p.x<q.x;
	}
};
typedef Vector point;
inline double dot(Vector p,Vector q){
	return p.x*q.x+p.y*q.y;
}
inline double dist(point p,point q){
	return sqrt(dot(p-q,p-q));
}
inline double cross(Vector p,Vector q){
	return p.x*q.y-p.y*q.x;
}
Vector rotate(Vector a,double theta){
	return Vector(a.x*cos(theta)-a.y*sin(theta),a.x*sin(theta)+a.y*cos(theta));
}

double a,b,r;
int cnt=0;
point p[maxn*4+5];
int top=0;
point s[maxn*4+5];
int cmp(point x,point y){
	double ang=cross(x-p[1],y-p[1]);
	if(fabs(ang)<eps) return dist(p[1],x)<dist(p[1],y);
	else return ang>eps;
}

int main(){
	double x,y,theta;
	Vector d[5];
	scanf("%d",&n);
	scanf("%lf %lf %lf",&a,&b,&r);
	a-=2*r;
	b-=2*r;
	d[1]=Vector(-b/2,a/2);
	d[2]=Vector(-b/2,-a/2);
	d[3]=Vector(b/2,a/2);
	d[4]=Vector(b/2,-a/2);
	for(int i=1;i<=n;i++){
		scanf("%lf %lf %lf",&x,&y,&theta);
		for(int j=1;j<=4;j++){
			p[++cnt]=point(x,y)+rotate(d[j],theta);
		}
	}
#ifdef DEBUG
	printf("%d\n",cnt);
	for(int i=1;i<=cnt;i++){
		printf("(%.2f,%.2f)\n",p[i].x,p[i].y);
	}
#endif
	for(int i=1;i<=cnt;i++){
		if(p[i]<p[1]) swap(p[1],p[i]);
	}
	sort(p+2,p+1+cnt,cmp);
	for(int i=1;i<=cnt;i++){
		while(top>1&&cross(s[top]-s[top-1],p[i]-s[top-1])<=eps) top--;
		s[++top]=p[i];
	}
	double ans=0;
	for(int i=1;i<top;i++) ans+=dist(s[i],s[i+1]);
	ans+=dist(s[top],s[1]);
	ans+=2*PI*r;
	printf("%.2lf\n",ans);
}