[HDU 5293]Tree chain problem(树形dp+树链剖分)

[HDU 5293]Tree chain problem(树形dp+树链剖分)

题面

在一棵树中，给出若干条链和链的权值，求选取不相交的链使得权值和最大。

分析

考虑树形dp，dp[x]表示以x为子树的最大权值和（选的链都在i的子树中）

设sum[x]表示x的儿子的dp值和，即\(\sum _{y \in \mathrm{son}(x)} dp[y]\)

1.不选两端点lca为x的链，dp[x]=sum[x]

2.选两端点lca为x的链，则dp[x]=max{链的权值+链上节点的所有子节点dp的和 - 链上节点dp和}（因为x的子节点也可能在链上，要去掉），这样选的链一定和lca为x的链不相交。取max即可得到答案。如果不理解，请看下图。

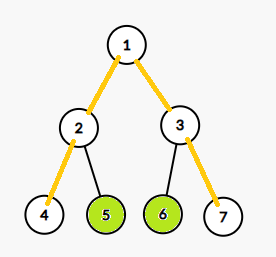
路径为4->7,如果直接对sum求和，我们会把2,3,4,5,6,7都算进答案，但实际上我们只需要5,6,所以再做一次减法，把4->7路径上的点减掉就可以了

预处理的时候可以保存两端点lca为x的链的编号。看到路径求和，我们直接用树链剖分维护即可。从下到上dp,一边更新dp值和sum值，一边求和。

时间复杂度\(O(n\log^2n)\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define maxn 100000
#define maxm 100000
using namespace std;
int t,n,m;
struct edge{
	int from;
	int to;
	int next;
}E[maxn*2+5];
int head[maxn+5];
int esz=1;
void add_edge(int u,int v){
	esz++;
	E[esz].from=u;
	E[esz].to=v;
	E[esz].next=head[u];
	head[u]=esz;
}	

struct segment_tree{
	struct node{
		int l;
		int r;
		long long sum;
	}tree[maxn*4+5];
	void push_up(int pos){
		tree[pos].sum=tree[pos<<1].sum+tree[pos<<1|1].sum;
	}
	void build(int l,int r,int pos){
		tree[pos].l=l;
		tree[pos].r=r;
		tree[pos].sum=0;
		if(l==r) return;
		int mid=(l+r)>>1;
		build(l,mid,pos<<1);
		build(mid+1,r,pos<<1|1);
		push_up(pos);
	}
	void update(int upos,long long uval,int pos){
		if(tree[pos].l==tree[pos].r){
			tree[pos].sum+=uval;
			return;
		}
		int mid=(tree[pos].l+tree[pos].r)>>1;
		if(upos<=mid) update(upos,uval,pos<<1);
		else update(upos,uval,pos<<1|1);
		push_up(pos);
	}
	long long query(int L,int R,int pos){
		if(L<=tree[pos].l&&R>=tree[pos].r){
			return tree[pos].sum;
		}
		int mid=(tree[pos].l+tree[pos].r)>>1;
		long long ans=0;
		if(L<=mid) ans+=query(L,R,pos<<1);
		if(R>mid) ans+=query(L,R,pos<<1|1);
		return ans;
	}
}T1,T2;//T1维护sum,T2维护dp 
int tim;
int sz[maxn+5],deep[maxn+5],dfn[maxn+5],top[maxn+5],son[maxn+5],fa[maxn+5];
void dfs1(int x,int f){
	fa[x]=f;
	sz[x]=1;
	deep[x]=deep[f]+1;
	for(int i=head[x];i;i=E[i].next){
		int y=E[i].to;
		if(y!=f){
			dfs1(y,x);
			sz[x]+=sz[y];
			if(sz[y]>sz[son[x]]) son[x]=y;
		}
	}
}
void dfs2(int x,int t){
	top[x]=t;
	dfn[x]=++tim;
	if(son[x]) dfs2(son[x],t);
	for(int i=head[x];i;i=E[i].next){
		int y=E[i].to;
		if(y!=fa[x]&&y!=son[x]){
			dfs2(y,y);
		}
	}
}
int lca(int x,int y){
	while(top[x]!=top[y]){
		if(deep[top[x]]>deep[top[y]]) x=fa[top[x]];
		else y=fa[top[y]];
	}
	if(deep[x]<deep[y]) return x;
	else return y;
}

void update_point(int x,long long uval,segment_tree &T){
	T.update(dfn[x],uval,1);
}
long long query_route(int x,int y,segment_tree &T){
	int tx=top[x];
	int ty=top[y];
	long long ans=0;
	while(tx!=ty){
		if(deep[tx]<deep[ty]){
			swap(tx,ty);
			swap(x,y);
		}
		ans+=T.query(dfn[tx],dfn[x],1);
		x=fa[tx];
		tx=top[x];
	}
	if(deep[x]>deep[y]) swap(x,y);
	ans+=T.query(dfn[x],dfn[y],1);
	return ans;
}

struct route{
	int x;
	int y;
	int lc;
	long long w;
}q[maxm+5];
vector<int>rid[maxn+5];//两端点lca为x的链的编号

long long sum[maxn+5];//sum(dp[son(x)])
long long dp[maxn+5];
void dfs3(int x){//dp过程
	sum[x]=0;
	for(int i=head[x];i;i=E[i].next){
		int y=E[i].to;
		if(y!=fa[x]){
			dfs3(y);
			sum[x]+=dp[y];
		}
	}
	dp[x]=sum[x];
	update_point(x,sum[x],T1);//因为下一步就要用到，这里要更新sum[x]
	for(int i=0;i<rid[x].size();i++){
		int k=rid[x][i];
		dp[x]=max(dp[x],q[k].w+query_route(q[k].x,q[k].y,T1)-query_route(q[k].x,q[k].y,T2));
	}
	update_point(x,dp[x],T2);
}

void ini(){
	memset(deep,0,sizeof(deep));
	memset(dfn,0,sizeof(dfn));
	memset(dp,0,sizeof(dp));
	memset(fa,0,sizeof(fa));
	memset(head,0,sizeof(head));
	for(int i=1;i<=n;i++) rid[i].clear();
	memset(son,0,sizeof(son));
	memset(sum,0,sizeof(sum));
	esz=1;
	memset(sz,0,sizeof(sz));
	tim=0;
	memset(top,0,sizeof(top));
	T1.build(1,n,1);
	T2.build(1,n,1);
}
int main(){
	int u,v,w;
	scanf("%d",&t);
	while(t--){
		scanf("%d %d",&n,&m);
		ini();
		for(int i=1;i<n;i++){
			scanf("%d %d",&u,&v);
			add_edge(u,v);
			add_edge(v,u);
		}
		dfs1(1,0);
		dfs2(1,1);
		for(int i=1;i<=m;i++){
			scanf("%d %d %lld",&q[i].x,&q[i].y,&q[i].w);
			q[i].lc=lca(q[i].x,q[i].y);
			rid[q[i].lc].push_back(i);
		}
		dfs3(1);
		printf("%lld\n",dp[1]);
	}
	
}