线性代数基础 矩阵

线性代数基础

标量 scalar

        单独的数，自然数，整数，实数、、、

        斜体小写，表示

向量 vector

• 一组一维数组
• 有序的一列数，一般定义纵向量。
• 但是，书写不方便，多使用向量的转置的进行书写
• 通常用粗体的小写变量名称表示向量，如 x
• 向量的一组元素，定义集合S={1,3,6}，然后写做 xs

• 向量的元素用带脚标的斜体表示，如向量 x的第1个元素为 x1，第2个元素x2
• 向量的一组元素，定义集合S={1,3,6}，然后写做 xs

矩阵 matrix

        二维数组

通常用粗体的大写变量名称表示矩阵，如 A

• 通常用粗体的大写变量名称表示矩阵，如 A

• A_i,j 表示矩阵第 i 行，第 j 列的元素
• f(A)_i,j表示函数 f 作用在 A 上输出矩阵的第 i行第 j 列元素。
• 在数据中，一般一行代表

张量 tensor

• 超过二维的数组
• Shape指的是张量的维度
• Shape（2，5）表示2行5列的矩阵
• 比如shape是（2，3，4）的张量
• Tensorflow：张量流
• 标量，向量，矩阵也都是特殊的张量

转置

• 向量的行列转换
• 以对角线为轴的镜像
• 矩阵转置，满足
• 
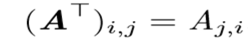
• 向量可以看作只有一列的矩阵，其转置可以看作只有一行的矩阵，如定义一个向量：

• 标量只有一个元素，转置等于其本身，

矩阵加法

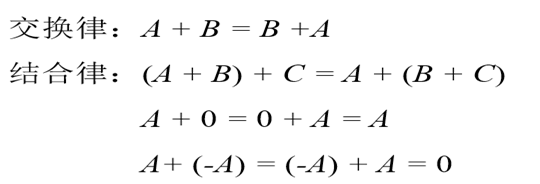
矩阵减法

 

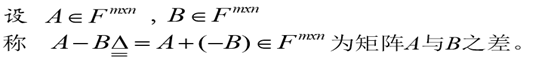
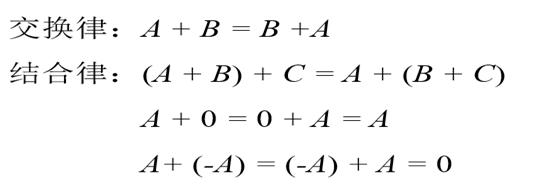
矩阵乘法

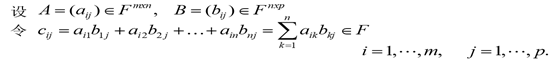
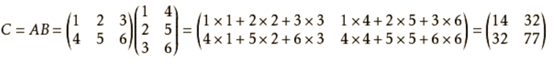
最终结果为 A的行Xb的列的新矩阵

矩阵乘法公式

        

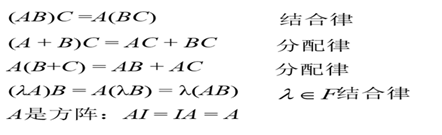
矩阵元素对应乘积 element wise product

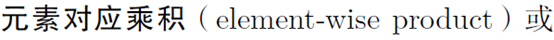
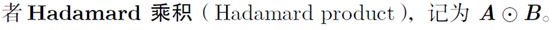
        Shape相同使用的一种乘积

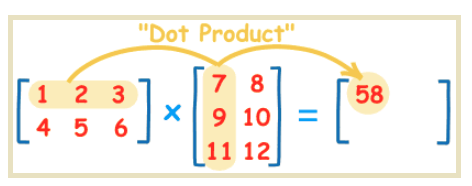
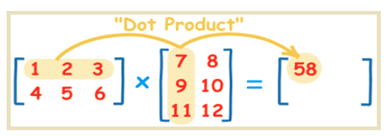
矩阵点积 dot product

 

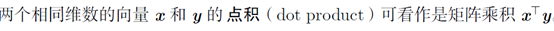
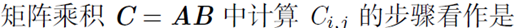
对于一维数组来说shape为数组元素的个数

        向量的点积为标量，一个数值

 

        两个向量点积示例

x = [1,2,3]^T

y = [7,9,11]^T

x.y = x^Ty = [1,2,3].[7,9,11]^T = 58

单位矩阵

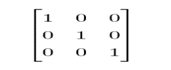单位矩阵的结构很简单：所有沿主对角线的元素都是 1，而其他位置的元素都是 0

• 性质：任意向量、矩阵和单位矩阵相乘，都不会改变。
• 单位矩阵的行列一致
• 一般将保持 n 维向量不变的单位矩阵记作
• 形式上：

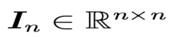
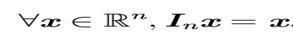
线性方程组

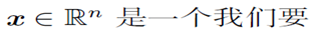
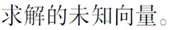
        矩阵是解线性方程组的重要工具

        线性方程组另一种书写方式

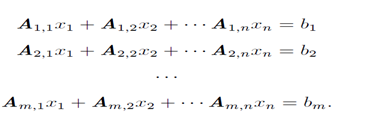
逆矩阵

• 一个矩阵乘以目标矩阵的结果为单位矩阵，则目标矩可逆，
• 且该矩阵为目标矩阵的逆矩阵
• 矩阵逆矩阵记作满足如下条件：

  

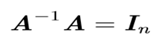
• 给定，

  

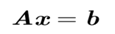
• 我们可以通过以下步骤求解向量