概率基础-随机试验-古典概型-几何概型

概率基础-随机试验-古典概型-几何概型

1 随机试验

    对某种自然现象做一次观察或者进行一次科学实验

    

实验特点：

1. 可以在相同的条件下进行
2. 实验的结果可能不止一个，但是实验前知道所有的可能结果
3. 实验前不知道哪个结果会出现，即实验结果等概率随机

随机实验示例：

    

            

 

2 样本空间

    随机实验E所有的可能的结果组成的集合，称为E的样本空间，记为S。

    其中，E的每个可能的结果，称为样本点

    

    样本空间示例：

        

3 事件

    样本空间S的某个子集， 为随机事件，大写字母A, B, C表示

 

    事件示例：

        

 

1. 每次实验中，事件中的某个样本点出现，则称 事件发生
2. 必然事件： 每个实验中一定会发生的事件
3. 不可能事件：每个实验中，一定不会发赛的事件

 

4 事件之间的关系

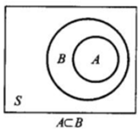
    4.1 包含关系：

        A发生，B一定发生

        B发生，A不一定发生

        

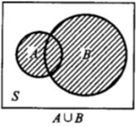
    4.2 和事件

        A发生，或者B发生，或者AB同时发生

        

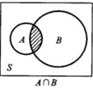
    4.3 积事件

1. B同时发生

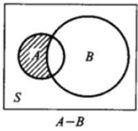
    4.4 差事件

        A发生， B不发生

        

    4.5 互斥事件

        交集为空

        互不相容事件

        不可能同时发生事件

        A发生，B就不发生

        B发生，A就不发生

        A，B 都不发生

        

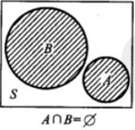
    4.6 逆事件 对立事件

        有且仅必有一件事发生

        A发生，B就不发生

        B发生，A就不发生

        必须有一件发生， 两事件的发生概率和为E

        

 

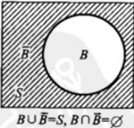
5 事件运算定律

    5.1 交换、结合、分配、摩根

        本质：既定概率的事件的发生顺序，并不影响组合环境下的事情发生概率。

             事件发生的顺序，不影响概率

             该来的都得来，早晚而已

    5.2 交换律

        

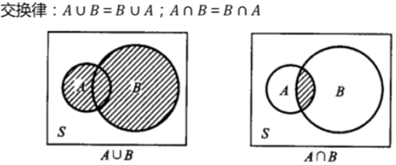
    5.3 结合律

        

    5.4 分配率

        

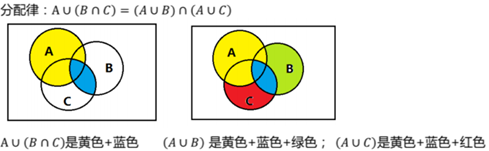
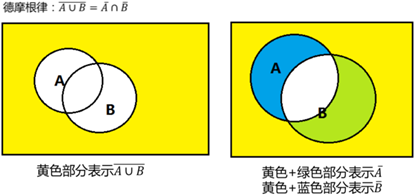
    5.5 摩根率

        不管早发生，还是晚发生，该发生的还得发生

        不管一个一个发生，还是一起发生，最终，结果一样

        

 

 

5 频率

    ，

        概率一定的重复实验，次数越多，事件发生的频率越趋于稳定（逐渐趋于概率）

        

        概率：事件的频率成为概率的条件

            不为负

            规范性：必然事件概率为1，不可能事件概率为0

            可列可加性：事件之间的概率可以进行条件运算

6 事件的性质

    

7 古典概型

    对于事件E满足以下条件称为实验的概率类型为古典概型

1. 实验样本空间为有限个元素（事件的可能结果有限）
2. 实验中每个基本事件发生的可能性相同，每个事件发生的概率论相等

注：

    基本事件：一个事件中的基本构成事件 骰子偶数中 2点、4点、、、

    事件：可能由多个基本事件构成 例如骰子偶数

 

        古典概型的计算：

            

8 排列组合 Permutation and Combination

    8.1 排列 A(n，m)

        从n个不同的元素中，取出m个元素，并且按照一定的顺序排成一列（取排）

        

    8.2 组合 C(n，m)

        从n个不同的元素中，取出m个元素，组成一组（仅取不排）

        

 

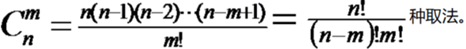
9 几何概型 等可能概型

    对于实验E满足：

1. 实验样本空间包含无限个元素
2. 实验中每个基本事件发生的可能性相同，即每个基本事件的概率相同

这样的实验E称为几何模型

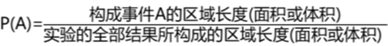
示例：

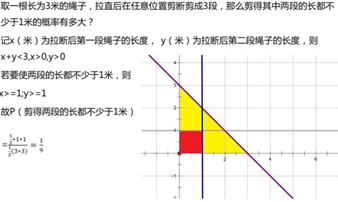
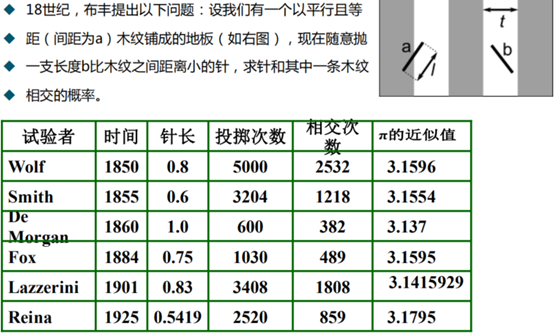
10 布丰投针实验 buffon