八大排序算法
冒泡排序
- 思想
- 通过对待排序序列从前向后依次比较相邻元素的值, 若发现逆序则交换, 使值较大的元素逐渐从前移向后部, 就像水底下的气泡一样逐渐向上冒.
- 优化
- 因为排序的过程中, 各元素不断接近自己的位置, 如果一趟比较下来没有进行过交换, 说明序列有序了.因此要在排序的过程中设置一个flag判断元素是否进行过交换, 从而减少不必要的比较.
- 代码
public static void bubbleSort(int[] arr) { boolean flag = false; for(int i = 0; i < arr.length - 1; i++) { for(int j = 0; j < arr.length-1-i; j++) { if(arr[j] > arr[j+1]) { swap(arr, j, j+1); flag = true; } } if(!flag) { return; } flag = false; } } private static void swap(int[] arr, int j, int i) { int temp = arr[j]; arr[j] = arr[i]; arr[i] = temp; }
选择排序
- 基本介绍
- 是从欲排序的数据中, 按指定的规则选出某一元素, 再依规定交换位置后达到排序的目的.
- 基本思想
- 第一次从arr[0]到arr[n-1]中选取最小值, 与arr[0]交换.
- 第二次从arr[1]到arr[n-1]中选取最小值, 与arr[1]交换,
- ......
- 代码
public static void selectSort(int[] arr) { for (int i = 0; i < arr.length - 1; i++) { for (int j = i + 1; j < arr.length; j++) { if (arr[i] > arr[j]) { swap(arr, i, j); } } } } private static void swap(int[] arr, int j, int i) { int temp = arr[j]; arr[j] = arr[i]; arr[i] = temp; }
插入排序
- 介绍
- 是对于欲排序的元素以插入的方式找该元素适当位置, 以达到排序的目的.
- 思想
- 把n个待排序的元素看成一个有序表和一个无序表, 开始时有序表只有一个元素, 无序表有n-1个元素, 排序过程中每次从无序表中取出第一个元素, 把它的排序码依次与有序表元素的排序码比较, 将它插入到有序表中的适当位置.
- 代码
public static void insertSort(int[] arr) { int i, j, temp; for (i = 0; i < arr.length; i++) { temp = arr[i]; j = i - 1; while (j >= 0 && temp < arr[j]) { arr[j + 1] = arr[j]; j--; } arr[j + 1] = temp; } }
快速排序
- 介绍
- quickSort是对冒泡排序的一种改进.
- 基本思想: 通过一趟排序将要排序的数据分隔为独立的两部分, 其中一部分的所有数据比另一部分的所有数据都小, 然后按此方法对两部分数据分别快排, (整个排序过程可以看成一个递归过程), 依此下去, 直到有序.
- 代码
public static void quickSort(int[] arr, int left, int right) { int l = left; // 左索引 int r = right; // 右索引 // int mid = arr[(int)Math.random()*(right-left+1)+left]; int mid = arr[(left + right) / 2]; // while循环的目的是让比mid小的放到其左边, 比mid大的值放到右边. while (l < r) { // 在mid左边一直找, 直到找到>=mid的值 while (arr[l] < mid) { l++; } // 在mid右边一直找, 直到找到<=mid的值 while (arr[r] > mid) { r--; } // 如果 l>=r 成立, 说明mid左右两边的值已经按照左边都<=mid, 右边都>=mid了. if (l >= r) break; // 交换 swap(arr, l, r); // 如果交换完后, 发现arr[l] == mid, 让r-- if (arr[l] == mid) r--; // 如果交换完后, 发现arr[r] == mid, 让l++ if (arr[r] == mid) l++; } // 如果l==r, 必须l++, r--, 否则栈溢出 if (l == r) { l++; r--; } // 向左递归 if (left < r) quickSort(arr, left, r); // 向右递归 if (right > l) quickSort(arr, l, right); }
希尔排序
- 概述
- 希尔排序也是一种插入排序, 它是简单插入排序经过改进后的高效版本, 也叫缩小增量排序.
- 基本思想
- 把记录按下标的一定增量分组, 对每组使用直接插入排序算法排序, 随着增量逐渐减少, 每组包含的关键词变多, 当增量减至1时, 整个文件恰好被分为一组, 算法终止.
- 代码
- 交换式, 很垃圾, 比插入排序还慢
public static void shellSort(int[] arr) { int gap = arr.length / 2; while (gap > 0) { for (int i = gap; i < arr.length; i++) { for (int j = i - gap; j >= 0; j -= gap) { if (arr[j] > arr[j + gap]) swap(arr, j, j + gap); } } gap /= 2; } }
- 移动式
public static void shellSort(int[] arr) { int i, j, temp; int gap = arr.length / 2; while (gap > 0) { for (i = gap; i < arr.length; i++) { j = i; temp = arr[i]; if (arr[j] < arr[j - gap]) { while (j - gap >= 0 && temp < arr[j - gap]) { arr[j] = arr[j - gap]; j -= gap; } arr[j] = temp; } } gap /= 2; } }
- 交换式, 很垃圾, 比插入排序还慢
归并排序
- 介绍
- 采取分治策略
- 分: 把问题分成一些小的问题然后递归求解
- 治: 把分的阶段得到的各答案"修补"在一起, 即分而治之.
- 采取分治策略
- 代码
// 分+合的方法 public static void mergeSort(int[] arr, int left, int right, int[] temp) { if (left < right) { int mid = (left + right) / 2; // 中间的索引 // 向左递归进行分解 mergeSort(arr, left, mid, temp); // 向右递归进行分解 mergeSort(arr, mid + 1, right, temp); // 合并 merge(arr, left, mid, right, temp); } } // 合并的方法 public static void merge(int[] arr, int left, int mid, int right, int[] temp) { int i = left; // 初始化i, 左边有序序列的初始索引 int j = mid + 1; // 初始化j, 右边有序序列的初始索引 int t = 0; // 指向temp数组的当前索引 // 先把左右两边(有序)的数据按照规则填充到temp数组, 直到有一边全部处理完毕 while (i <= mid && j <= right) { if (arr[i] <= arr[j]) { temp[t++] = arr[i++]; } else { temp[t++] = arr[j++]; } } // 把剩余的填充到temp数组中 while (i <= mid) { temp[t++] = arr[i++]; } while (j <= right) { temp[t++] = arr[j++]; } // 将temp数组的元素拷贝到arr // 并不是每次都拷贝所有的 t = 0; int tempLeft = left; while (tempLeft <= right) { arr[tempLeft++] = temp[t++]; } }
基数排序
- 介绍
- 属于分配式排序, 又称桶排序, 顾名思义, 它是通过键值的各个位的值, 将要排序的元素分配至某些桶中, 达到排序的作用.
- 是将整数按位数切割成不同的数字, 然后按每个位数分别比较.
- 基本思想
- 将所有待比较数值统一为同样的数位长度, 数位短的数前面补零, 然后从最低位开始, 依次进行依次排序, 这样从最低位排序一直到最高位排序完成以后, 数列就有序了.
- 第一轮: 将每个元素的个位数取出, 然后看这个数应该放在哪个对应的桶, 按照这个桶的顺序(一维数组的下标依次取出数据, 放入原来数组)
- 第二轮: 将每个元素的十位数取出, 然后看这个数该放入哪个对应的桶, 按照这个桶的顺序(一维数组的下标依次取出数据, 放入原来数组)
- 依次下去, 直到有序
- 小数不能用基数排序
- 代码
//该代码仅仅实现了非负数的排序, 若有负数出现, 则会ArrayIndexOutOfBoundsException public static void radixSort(int[] arr) { int[][] bucket = new int[10][arr.length]; int[] cnt = new int[10]; int max = arr[0]; for (int i = 1; i < arr.length; i++) { if (arr[i] > max) max = arr[i]; } int maxLen = ("" + max).length(); for (int i = 0, n = 1; i < maxLen; i++, n *= 10) { for (int j = 0; j < arr.length; j++) { int digit = arr[j] / n % 10; bucket[digit][cnt[digit]++] = arr[j]; } int index = 0; for (int k = 0; k < arr.length; k++) { if (cnt[k] != 0) { for (int l = 0; l < cnt[k]; l++) arr[index++] = bucket[k][l]; } cnt[k] = 0; } } }
- 一轮一轮的讲解
public static void radixSort(int[] arr) { // 定义一个二维数组表示10个桶, 每个桶就是一个一维数组 // 为了防止放数时数据溢出, 则每个桶的大小定为arr.length // 很明显, 基数排序是用空间换时间的经典算法. int[][] bucket = new int[10][arr.length]; // 为了记录每个桶中实际存放了多少个数据, 我们定义一个一维数组来记录各个桶每次放入数据个数 int[] cnt = new int[10]; // 第一轮(针对每个元素的个位进行排序处理) for (int i = 0; i < arr.length; i++) { // 取出每个元素的个位 int digit = arr[i] % 10; // 放入到对应桶中 bucket[digit][cnt[digit]++] = arr[i]; } // 按照桶的顺序, 放入原来数组 int index = 0; // 遍历每个桶, 并将每个桶中数据放入原数组 for (int i = 0; i < cnt.length; i++) { // 如果桶中有数据, 才放入到原数组 if (cnt[i] != 0) { // 循环第i个桶, 放入数据即可 for (int j = 0; j < cnt[i]; j++) { arr[index++] = bucket[i][j]; } } // 第一轮结束把cnt数组清空 cnt[i] = 0; } System.out.println("第一轮对个位的处理: " + Arrays.toString(arr)); // 第二轮(针对每个元素的十位进行排序处理) for (int i = 0; i < arr.length; i++) { // 取出每个元素的十位 int digit = arr[i] / 10 % 10; // 放入到对应桶中 bucket[digit][cnt[digit]++] = arr[i]; } // 按照桶的顺序, 放入原来数组 index = 0; // 遍历每个桶, 并将每个桶中数据放入原数组 for (int i = 0; i < cnt.length; i++) { // 如果桶中有数据, 才放入到原数组 if (cnt[i] != 0) { // 循环第i个桶, 放入数据即可 for (int j = 0; j < cnt[i]; j++) { arr[index++] = bucket[i][j]; } } cnt[i] = 0; } System.out.println("第二轮对个位的处理: " + Arrays.toString(arr)); // 第三轮(针对每个元素的百位进行排序处理) for (int i = 0; i < arr.length; i++) { // 取出每百元素的个位 int digit = arr[i] / 100 % 10; // 放入到对应桶中 bucket[digit][cnt[digit]++] = arr[i]; } // 按照桶的顺序, 放入原来数组 index = 0; // 遍历每个桶, 并将每个桶中数据放入原数组 for (int i = 0; i < cnt.length; i++) { // 如果桶中有数据, 才放入到原数组 if (cnt[i] != 0) { // 循环第i个桶, 放入数据即可 for (int j = 0; j < cnt[i]; j++) { arr[index++] = bucket[i][j]; } } cnt[i] = 0; } System.out.println("第三轮对个位的处理: " + Arrays.toString(arr)); }
堆排序
################
总结
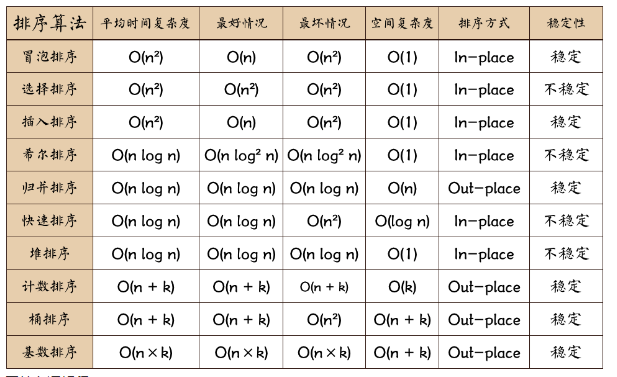
- In-place: 不占用额外内存, Out-place: 占用额外内存




